Probability distribution
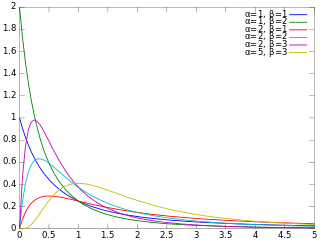
Бета-прайм Функция плотности вероятности
Кумулятивная функция распределения
Параметры α > 0 {\displaystyle \alpha >0} форма ( настоящая ) β > 0 {\displaystyle \beta >0} Поддерживать x ∈ [ 0 , ∞ ) {\displaystyle x\in [0,\infty )\!} PDF f ( x ) = x α − 1 ( 1 + x ) − α − β B ( α , β ) {\displaystyle f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{B(\alpha ,\beta )}}\!} CDF I x 1 + x ( α , β ) {\displaystyle I_{{\frac {x}{1+x}}(\alpha ,\beta )}} I x ( α , β ) {\displaystyle I_{x}(\alpha ,\beta )} Иметь в виду α β − 1 if β > 1 {\displaystyle {\frac {\alpha }{\beta -1}}{\text{ if }}\beta >1} Режим α − 1 β + 1 if α ≥ 1 , 0 otherwise {\displaystyle {\frac {\alpha -1}{\beta +1}}{\text{ if }}\alpha \geq 1{\text{, 0 otherwise}}\!} Дисперсия α ( α + β − 1 ) ( β − 2 ) ( β − 1 ) 2 if β > 2 {\displaystyle {\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}{\text{ if }}\beta >2} асимметрия 2 ( 2 α + β − 1 ) β − 3 β − 2 α ( α + β − 1 ) if β > 3 {\displaystyle {\frac {2(2\alpha +\beta -1)}{\beta -3}}{\sqrt {\frac {\beta -2}{\alpha (\alpha +\beta -1)}}}{\text{ if }}\beta >3} МГФ Не существует CF e − i t Γ ( α + β ) Γ ( β ) G 1 , 2 2 , 0 ( α + β β , 0 | − i t ) {\displaystyle {\frac {e^{-it}\Gamma (\alpha +\beta )}{\Gamma (\beta )}}G_{1,2}^{\,2,0}\!\left(\left.{\begin{matrix}\alpha +\beta \\\beta ,0\end{matrix}}\;\right|\,-it\right)}
В теории вероятностей и статистике бета -распределение (также известное как инвертированное бета-распределение или бета-распределение второго рода) [1] абсолютно непрерывным распределением вероятностей . Если p ∈ [ 0 , 1 ] {\displaystyle p\in [0,1]} бета-распределение , то шансы p 1 − p {\displaystyle {\frac {p}{1-p}}}
Бета-простое распределение определяется для x > 0 {\displaystyle x>0} α и β , имеющими функцию плотности вероятности :
f ( x ) = x α − 1 ( 1 + x ) − α − β B ( α , β ) {\displaystyle f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{B(\alpha ,\beta )}}} где B — бета-функция .
Кумулятивная функция распределения равна
F ( x ; α , β ) = I x 1 + x ( α , β ) , {\displaystyle F(x;\alpha ,\beta )=I_{\frac {x}{1+x}}\left(\alpha ,\beta \right),} где I — регуляризованная неполная бета-функция .
Ожидаемое значение, дисперсия и другие детали распределения указаны в боковом окне; для β > 4 {\displaystyle \beta >4} избыточный эксцесс
γ 2 = 6 α ( α + β − 1 ) ( 5 β − 11 ) + ( β − 1 ) 2 ( β − 2 ) α ( α + β − 1 ) ( β − 3 ) ( β − 4 ) . {\displaystyle \gamma _{2}=6{\frac {\alpha (\alpha +\beta -1)(5\beta -11)+(\beta -1)^{2}(\beta -2)}{\alpha (\alpha +\beta -1)(\beta -3)(\beta -4)}}.} В то время как соответствующее бета-распределение представляет собой сопряженное априорное распределение параметра распределения Бернулли, выраженное как вероятность, бета-распределение простых чисел представляет собой сопряженное априорное распределение параметра распределения Бернулли, выраженное в коэффициентах . Распределение представляет собой распределение Пирсона VI типа . [1]
Мода переменной X распределяется как β ′ ( α , β ) {\displaystyle \beta '(\alpha ,\beta )} X ^ = α − 1 β + 1 {\displaystyle {\hat {X}}={\frac {\alpha -1}{\beta +1}}} α β − 1 {\displaystyle {\frac {\alpha }{\beta -1}}} β > 1 {\displaystyle \beta >1} β ≤ 1 {\displaystyle \beta \leq 1} α ( α + β − 1 ) ( β − 2 ) ( β − 1 ) 2 {\displaystyle {\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}} β > 2 {\displaystyle \beta >2}
Для − α < k < β {\displaystyle -\alpha <k<\beta } k -й момент E [ X k ] {\displaystyle E[X^{k}]}
E [ X k ] = B ( α + k , β − k ) B ( α , β ) . {\displaystyle E[X^{k}]={\frac {B(\alpha +k,\beta -k)}{B(\alpha ,\beta )}}.} Для k ∈ N {\displaystyle k\in \mathbb {N} } k < β , {\displaystyle k<\beta ,}
E [ X k ] = ∏ i = 1 k α + i − 1 β − i . {\displaystyle E[X^{k}]=\prod _{i=1}^{k}{\frac {\alpha +i-1}{\beta -i}}.} CDF также можно записать как
x α ⋅ 2 F 1 ( α , α + β , α + 1 , − x ) α ⋅ B ( α , β ) {\displaystyle {\frac {x^{\alpha }\cdot {}_{2}F_{1}(\alpha ,\alpha +\beta ,\alpha +1,-x)}{\alpha \cdot B(\alpha ,\beta )}}} где 2 F 1 {\displaystyle {}_{2}F_{1}} – гипергеометрическая функция 2 F 1 .
Бета-распределение простых чисел также может быть перепараметризовано с точки зрения его среднего значения μ > 0 и точности ν > 0 параметров ( [2]
Рассмотрим параметризацию µ = α /( β -1) и ν = β – 2, т. е. α = µ ( 1 + ν ) и β знак равно 2 + ν . При этой параметризацииE[Y] = µ и Var[Y] = µ (1 + µ )/ ν .
Можно добавить еще два параметра, чтобы сформировать обобщенное простое бета-распределение. β ′ ( α , β , p , q ) {\displaystyle \beta '(\alpha ,\beta ,p,q)}
имеющая функцию плотности вероятности :
f ( x ; α , β , p , q ) = p ( x q ) α p − 1 ( 1 + ( x q ) p ) − α − β q B ( α , β ) {\displaystyle f(x;\alpha ,\beta ,p,q)={\frac {p\left({\frac {x}{q}}\right)^{\alpha p-1}\left(1+\left({\frac {x}{q}}\right)^{p}\right)^{-\alpha -\beta }}{qB(\alpha ,\beta )}}} со средним
q Γ ( α + 1 p ) Γ ( β − 1 p ) Γ ( α ) Γ ( β ) if β p > 1 {\displaystyle {\frac {q\Gamma \left(\alpha +{\tfrac {1}{p}}\right)\Gamma (\beta -{\tfrac {1}{p}})}{\Gamma (\alpha )\Gamma (\beta )}}\quad {\text{if }}\beta p>1} и режим
q ( α p − 1 β p + 1 ) 1 p if α p ≥ 1 {\displaystyle q\left({\frac {\alpha p-1}{\beta p+1}}\right)^{\tfrac {1}{p}}\quad {\text{if }}\alpha p\geq 1} Обратите внимание, что если p = q = 1, то обобщенное бета-простое распределение сводится к стандартному бета-простому распределению .
Это обобщение можно получить с помощью следующего обратимого преобразования. Если y ∼ β ′ ( α , β ) {\displaystyle y\sim \beta '(\alpha ,\beta )} x = q y 1 / p {\displaystyle x=qy^{1/p}} q , p > 0 {\displaystyle q,p>0} x ∼ β ′ ( α , β , p , q ) {\displaystyle x\sim \beta '(\alpha ,\beta ,p,q)}
Сложное гамма-распределение [3] параметр масштаба q добавляется , но где p = 1. Оно названо так потому, что образуется путем объединения двух гамма-распределений :
β ′ ( x ; α , β , 1 , q ) = ∫ 0 ∞ G ( x ; α , r ) G ( r ; β , q ) d r {\displaystyle \beta '(x;\alpha ,\beta ,1,q)=\int _{0}^{\infty }G(x;\alpha ,r)G(r;\beta ,q)\;dr} где G ( x ; a , b ) {\displaystyle G(x;a,b)} a {\displaystyle a} b {\displaystyle b}
Режим, среднее значение и дисперсию составной гаммы можно получить путем умножения режима и среднего значения в приведенном выше информационном окне на q , а дисперсию на q. 2 .
Другой способ выразить начисление процентов: если r ∼ G ( β , q ) {\displaystyle r\sim G(\beta ,q)} x ∣ r ∼ G ( α , r ) {\displaystyle x\mid r\sim G(\alpha ,r)} x ∼ β ′ ( α , β , 1 , q ) {\displaystyle x\sim \beta '(\alpha ,\beta ,1,q)}
Если X ∼ β ′ ( α , β ) {\displaystyle X\sim \beta '(\alpha ,\beta )} 1 X ∼ β ′ ( β , α ) {\displaystyle {\tfrac {1}{X}}\sim \beta '(\beta ,\alpha )} Если Y ∼ β ′ ( α , β ) {\displaystyle Y\sim \beta '(\alpha ,\beta )} X = q Y 1 / p {\displaystyle X=qY^{1/p}} X ∼ β ′ ( α , β , p , q ) {\displaystyle X\sim \beta '(\alpha ,\beta ,p,q)} Если X ∼ β ′ ( α , β , p , q ) {\displaystyle X\sim \beta '(\alpha ,\beta ,p,q)} k X ∼ β ′ ( α , β , p , k q ) {\displaystyle kX\sim \beta '(\alpha ,\beta ,p,kq)} β ′ ( α , β , 1 , 1 ) = β ′ ( α , β ) {\displaystyle \beta '(\alpha ,\beta ,1,1)=\beta '(\alpha ,\beta )} Если X 1 ∼ β ′ ( α , β ) {\displaystyle X_{1}\sim \beta '(\alpha ,\beta )} X 2 ∼ β ′ ( α , β ) {\displaystyle X_{2}\sim \beta '(\alpha ,\beta )} Y = X 1 + X 2 ∼ β ′ ( γ , δ ) {\displaystyle Y=X_{1}+X_{2}\sim \beta '(\gamma ,\delta )} γ = 2 α ( α + β 2 − 2 β + 2 α β − 4 α + 1 ) ( β − 1 ) ( α + β − 1 ) {\displaystyle \gamma ={\frac {2\alpha (\alpha +\beta ^{2}-2\beta +2\alpha \beta -4\alpha +1)}{(\beta -1)(\alpha +\beta -1)}}} δ = 2 α + β 2 − β + 2 α β − 4 α α + β − 1 {\displaystyle \delta ={\frac {2\alpha +\beta ^{2}-\beta +2\alpha \beta -4\alpha }{\alpha +\beta -1}}} В более общем смысле, пусть X 1 , . . . , X n n {\displaystyle X_{1},...,X_{n}n} ∀ i , 1 ≤ i ≤ n , X i ∼ β ′ ( α , β ) {\displaystyle \forall i,1\leq i\leq n,X_{i}\sim \beta '(\alpha ,\beta )} S = X 1 + . . . + X n ∼ β ′ ( γ , δ ) {\displaystyle S=X_{1}+...+X_{n}\sim \beta '(\gamma ,\delta )} γ = n α ( α + β 2 − 2 β + n α β − 2 n α + 1 ) ( β − 1 ) ( α + β − 1 ) {\displaystyle \gamma ={\frac {n\alpha (\alpha +\beta ^{2}-2\beta +n\alpha \beta -2n\alpha +1)}{(\beta -1)(\alpha +\beta -1)}}} δ = 2 α + β 2 − β + n α β − 2 n α α + β − 1 {\displaystyle \delta ={\frac {2\alpha +\beta ^{2}-\beta +n\alpha \beta -2n\alpha }{\alpha +\beta -1}}} Если X ∼ F ( 2 α , 2 β ) {\displaystyle X\sim F(2\alpha ,2\beta )} F -распределение α β X ∼ β ′ ( α , β ) {\displaystyle {\tfrac {\alpha }{\beta }}X\sim \beta '(\alpha ,\beta )} X ∼ β ′ ( α , β , 1 , β α ) {\displaystyle X\sim \beta '(\alpha ,\beta ,1,{\tfrac {\beta }{\alpha }})} Если X ∼ Beta ( α , β ) {\displaystyle X\sim {\textrm {Beta}}(\alpha ,\beta )} X 1 − X ∼ β ′ ( α , β ) {\displaystyle {\frac {X}{1-X}}\sim \beta '(\alpha ,\beta )} Если X ∼ β ′ ( α , β ) {\displaystyle X\sim \beta '(\alpha ,\beta )} X 1 + X ∼ Beta ( α , β ) {\displaystyle {\frac {X}{1+X}}\sim {\textrm {Beta}}(\alpha ,\beta )} Для параметризации гамма-распределения I: Если X k ∼ Γ ( α k , θ k ) {\displaystyle X_{k}\sim \Gamma (\alpha _{k},\theta _{k})} X 1 X 2 ∼ β ′ ( α 1 , α 2 , 1 , θ 1 θ 2 ) {\displaystyle {\tfrac {X_{1}}{X_{2}}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\tfrac {\theta _{1}}{\theta _{2}}})} α 1 , α 2 , θ 1 θ 2 {\displaystyle \alpha _{1},\alpha _{2},{\tfrac {\theta _{1}}{\theta _{2}}}} Для параметризации гамма-распределения II: Если X k ∼ Γ ( α k , β k ) {\displaystyle X_{k}\sim \Gamma (\alpha _{k},\beta _{k})} X 1 X 2 ∼ β ′ ( α 1 , α 2 , 1 , β 2 β 1 ) {\displaystyle {\tfrac {X_{1}}{X_{2}}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\tfrac {\beta _{2}}{\beta _{1}}})} β k {\displaystyle \beta _{k}} β 2 β 1 {\displaystyle {\tfrac {\beta _{2}}{\beta _{1}}}} Если β 2 ∼ Γ ( α 1 , β 1 ) {\displaystyle \beta _{2}\sim \Gamma (\alpha _{1},\beta _{1})} X 2 ∣ β 2 ∼ Γ ( α 2 , β 2 ) {\displaystyle X_{2}\mid \beta _{2}\sim \Gamma (\alpha _{2},\beta _{2})} X 2 ∼ β ′ ( α 2 , α 1 , 1 , β 1 ) {\displaystyle X_{2}\sim \beta '(\alpha _{2},\alpha _{1},1,\beta _{1})} β k {\displaystyle \beta _{k}} β 1 {\displaystyle \beta _{1}} β ′ ( p , 1 , a , b ) = Dagum ( p , a , b ) {\displaystyle \beta '(p,1,a,b)={\textrm {Dagum}}(p,a,b)} распределение β ′ ( 1 , p , a , b ) = SinghMaddala ( p , a , b ) {\displaystyle \beta '(1,p,a,b)={\textrm {SinghMaddala}}(p,a,b)} -Маддалы . β ′ ( 1 , 1 , γ , σ ) = LL ( γ , σ ) {\displaystyle \beta '(1,1,\gamma ,\sigma )={\textrm {LL}}(\gamma ,\sigma )} Логистическое . Бета-простое распределение является частным случаем распределения Пирсона 6-го типа . Если X имеет распределение Парето с минимумом x m {\displaystyle x_{m}} α {\displaystyle \alpha } X x m − 1 ∼ β ′ ( 1 , α ) {\displaystyle {\dfrac {X}{x_{m}}}-1\sim \beta ^{\prime }(1,\alpha )} Если X имеет распределение Ломакса , также известное как распределение Парето типа II, с параметром формы α {\displaystyle \alpha } λ {\displaystyle \lambda } X λ ∼ β ′ ( 1 , α ) {\displaystyle {\frac {X}{\lambda }}\sim \beta ^{\prime }(1,\alpha )} Если X имеет стандартное распределение Парето типа IV с параметром формы α {\displaystyle \alpha } γ {\displaystyle \gamma } X 1 γ ∼ β ′ ( 1 , α ) {\displaystyle X^{\frac {1}{\gamma }}\sim \beta ^{\prime }(1,\alpha )} X ∼ β ′ ( 1 , α , 1 γ , 1 ) {\displaystyle X\sim \beta ^{\prime }(1,\alpha ,{\tfrac {1}{\gamma }},1)} Инвертированное распределение Дирихле является обобщением простого бета-распределения. Если X ∼ β ′ ( α , β ) {\displaystyle X\sim \beta '(\alpha ,\beta )} ln X {\displaystyle \ln X} обобщенное логистическое распределение . В более общем смысле, если X ∼ β ′ ( α , β , p , q ) {\displaystyle X\sim \beta '(\alpha ,\beta ,p,q)} ln X {\displaystyle \ln X} масштабированное и смещенное обобщенное логистическое распределение. Джонсон, Н.Л., Коц, С., Балакришнан, Н. (1995). Непрерывные одномерные распределения , Том 2 (2-е издание), Wiley. ISBN 0-471-58494-0 Бургиньон, М.; Сантос-Нето, М.; де Кастро, М. (2021), «Новая модель регрессии для положительных случайных величин с асимметричным и длинным хвостом», Metron , 79 : 33–55, doi : 10.1007/s40300-021-00203-y , S2CID 233534544
скрывать Дискретный
с конечным с бесконечным
Непрерывный
поддерживается на поддерживается на поддерживается при поддержке
Смешанный
Многомерный Направленный Выродиться единственное число Семьи












![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)














![{\displaystyle E[X^{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dcd54fe6c5cb4afbfcd7bd94c4778d13b8bbc3f)
![{\displaystyle E[X^{k}]={\frac {B(\alpha +k,\beta -k)}{B(\alpha,\beta)}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30c6530cfd83409026129cc40968169281f41081)


![{\displaystyle E[X^{k}]=\prod _{i=1}^{k}{\frac {\alpha +i-1}{\beta -i}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0f1689a0ef95460a83f9f53462da32a9b1e8f04)
































































