Генерализованное логистическое распределение

Термин «обобщенное логистическое распределение» используется как название нескольких различных семейств вероятностных распределений . Например, Джонсон и др. ^[1] перечислите четыре формы, которые перечислены ниже.

Тип I также называют неравномерным логистическим распределением . Тип IV включает в себя другие типы и получается при применении логит- преобразования к бета- случайным переменным. Следуя тому же соглашению, что и для логнормального распределения , тип IV можно назвать логистическим бета-распределением со ссылкой на стандартную логистическую функцию , которая является обратной логит-преобразованию.

Чтобы узнать о других семействах распределений, которые также называются обобщенными логистическими распределениями, см. смещенное логарифмическое логистическое распределение , которое является обобщением логарифмического логистического распределения ; и металогическое («металогистическое») распределение , которое является очень гибким по форме и границам и может быть адаптировано к данным с помощью линейного метода наименьших квадратов.

Определения

Следующие определения предназначены для стандартизированных версий семейств, которые можно расширить до полной формы как семейства в масштабе местоположения . Каждый из них определяется с использованием либо кумулятивной функции распределения ( F ), либо функции плотности вероятности ( ƒ ) и определяется на (-∞, ∞).

Тип I

F(x;\alpha )={\frac {1}{(1+e^{-x})^{\alpha }}}\equiv (1+e^{-x})^{-\alpha },\quad \alpha >0.

Соответствующая функция плотности вероятности:

f(x;\alpha )={\frac {\alpha e^{-x}}{\left(1+e^{-x}\right)^{\alpha +1}}},\quad \alpha >0.

Этот тип также получил название «асимметричного логистического» распределения.

Тип II

F(x;\alpha )=1-{\frac {e^{-\alpha x}}{(1+e^{-x})^{\alpha }}},\quad \alpha >0.

Соответствующая функция плотности вероятности:

f(x;\alpha )={\frac {\alpha e^{-\alpha x}}{(1+e^{-x})^{\alpha +1}}},\quad \alpha >0.

Тип III

f(x;\alpha )={\frac {1}{B(\alpha ,\alpha )}}{\frac {e^{-\alpha x}}{(1+e^{-x})^{2\alpha }}},\quad \alpha >0.

Здесь B — бета-функция . для Производящая функция момента этого типа равна

M(t)={\frac {\Gamma (\alpha -t)\Gamma (\alpha +t)}{(\Gamma (\alpha ))^{2}}},\quad -\alpha <t<\alpha .

Соответствующая кумулятивная функция распределения:

F(x;\alpha )={\frac {\left(e^{x}+1\right)\Gamma (\alpha )e^{\alpha (-x)}\left(e^{-x}+1\right)^{-2\alpha }\,_{2}{\tilde {F}}_{1}\left(1,1-\alpha ;\alpha +1;-e^{x}\right)}{B(\alpha ,\alpha )}},\quad \alpha >0.

Тип IV

{\begin{aligned}f(x;\alpha ,\beta )&={\frac {1}{B(\alpha ,\beta )}}{\frac {e^{-\beta x}}{(1+e^{-x})^{\alpha +\beta }}},\quad \alpha ,\beta >0\\[4pt]&={\frac {\sigma (x)^{\alpha }\sigma (-x)^{\beta }}{B(\alpha ,\beta )}}.\end{aligned}}

Где B — бета-функция и $\sigma (x)=1/(1+e^{-x})$ стандартная логистическая функция . для Производящая функция момента этого типа равна

M(t)={\frac {\Gamma (\beta -t)\Gamma (\alpha +t)}{\Gamma (\alpha )\Gamma (\beta )}},\quad -\alpha <t<\beta .

Этот тип еще называют «экспоненциальной обобщенной бета второго типа». ^[1]

Соответствующая кумулятивная функция распределения:

F(x;\alpha ,\beta )={\frac {\left(e^{x}+1\right)\Gamma (\alpha )e^{\beta (-x)}\left(e^{-x}+1\right)^{-\alpha -\beta }\,_{2}{\tilde {F}}_{1}\left(1,1-\beta ;\alpha +1;-e^{x}\right)}{B(\alpha ,\beta )}},\quad \alpha ,\beta >0.

Связь между типами

Тип IV — наиболее общая форма распределения. Распределение типа III можно получить из типа IV, зафиксировав $\beta =\alpha$ . Распределение типа II можно получить из типа IV, зафиксировав $\alpha =1$ (и переименование $\beta$ к $\alpha$ ). Распределение типа I можно получить из типа IV, зафиксировав $\beta =1$ . Исправление $\alpha =\beta =1$ дает стандартное логистическое распределение .

Объекты типа IV (логистический бета)

или Обобщенное логистическое распределение типа IV логистическое бета- распределение с поддержкой $x\in \mathbb {R}$ и параметры формы $\alpha ,\beta >0$ , имеет (как показано выше ) функцию плотности вероятности (pdf):

f(x;\alpha ,\beta )={\frac {1}{B(\alpha ,\beta )}}{\frac {e^{-\beta x}}{(1+e^{-x})^{\alpha +\beta }}}={\frac {\sigma (x)^{\alpha }\sigma (-x)^{\beta }}{B(\alpha ,\beta )}},

где $\sigma (x)=1/(1+e^{-x})$ стандартная логистическая функция . Функции плотности вероятности для трех различных наборов параметров формы показаны на графике, где распределения были масштабированы и сдвинуты для получения нулевых средних значений и единичной дисперсии, чтобы облегчить сравнение форм.

Далее обозначения $B_{\sigma }(\alpha ,\beta )$ используется для обозначения распределения типа IV.

Связь с гамма-распределением

Это распределение можно получить через гамма-распределение следующим образом. Позволять $y\sim {\text{Gamma}}(\alpha ,\gamma )$ и независимо , $z\sim {\text{Gamma}}(\beta ,\gamma )$ и пусть $x=\ln y-\ln z$ . Затем $x\sim B_{\sigma }(\alpha ,\beta )$ . ^[2]

Симметрия

Если $x\sim B_{\sigma }(\alpha ,\beta )$ , затем $-x\sim B_{\sigma }(\beta ,\alpha )$ .

Среднее и дисперсия

Используя логарифмические ожидания гамма-распределения, среднее значение и дисперсию можно получить как:

{\begin{aligned}{\text{E}}[x]&=\psi (\alpha )-\psi (\beta )\\{\text{var}}[x]&=\psi '(\alpha )+\psi '(\beta )\\\end{aligned}}

где $\psi$ — дигамма-функция , а $\psi '=\psi ^{(1)}$ является ее первой производной, также известной как тригамма-функция или первая полигамма-функция . С $\psi$ , строго возрастает знак среднего совпадает со знаком $\alpha -\beta$ . С $\psi '$ строго убывает, параметры формы также можно интерпретировать как параметры концентрации. Действительно, как показано ниже, левый и правый хвосты соответственно становятся тоньше по мере того, как $\alpha$ или $\beta$ увеличены. Два члена дисперсии представляют собой вклады в дисперсию левой и правой частей распределения.

Кумулянты и асимметрия

Кумулянтная производящая функция равна $K(t)=\ln M(t)$ , где производящая функция момента $M(t)$ дано выше . Кумулянты , $\kappa _{n}$ , являются $n$ -я производная от $K(t)$ , оцененный в $t=0$ :

\kappa _{n}=K^{(n)}(0)=\psi ^{(n-1)}(\alpha )+(-1)^{n}\psi ^{(n-1)}(\beta )

где $\psi ^{(0)}=\psi$ и $\psi ^{(n-1)}$ — дигамма и полигамма функции. В соответствии с приведенным выше выводом, первый кумулянт, $\kappa _{1}$ , является средним и вторым, $\kappa _{2}$ , — это дисперсия.

Третий кумулянт, $\kappa _{3}$ , – третий центральный момент $E[(x-E[x])^{3}]$ , что при масштабировании по третьей степени стандартного отклонения дает асимметрию :

{\text{skew}}[x]={\frac {\psi ^{(2)}(\alpha )-\psi ^{(2)}(\beta )}{{\sqrt {{\text{var}}[x]}}^{3}}}

Знак (а значит, и направленность ) асимметрии тот же, что и знак $\alpha -\beta$ .

Режим

Режим (максимум pdf) можно получить, найдя $x$ где производная журнала PDF равна нулю:

{\frac {d}{dx}}\ln f(x;\alpha ,\beta )=\alpha \sigma (-x)-\beta \sigma (x)=0

Это упрощает $\alpha /\beta =e^{x}$ , так что: ^[2]

{\text{mode}}[x]=\ln {\frac {\alpha }{\beta }}

Поведение хвоста

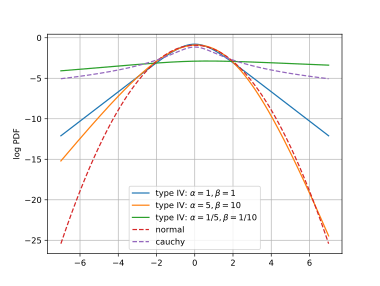
В каждом из левого и правого хвостов одна из сигмовидных фигур в PDF-файле насыщается до одной, так что хвост формируется другой сигмовидной. Для большого негатива $x$ , левый хвост PDF-файла пропорционален $\sigma (x)^{\alpha }\approx e^{\alpha x}$ , а правый хвост (большой положительный $x$ ) пропорциональна $\sigma (-x)^{\beta }\approx e^{-\beta x}$ . Это означает, что хвосты независимо контролируются $\alpha$ и $\beta$ . Хотя хвосты типа IV тяжелее, чем хвосты нормального распределения ( $e^{-{\frac {x^{2}}{2v}}}$ , для отклонения $v$ ), средние и дисперсии типа IV остаются конечными для всех $\alpha ,\beta >0$ . Это контрастирует с распределением Коши , для которого не существует среднего и дисперсии. На показанных здесь графиках log pdf хвосты типа IV являются линейными, хвосты нормального распределения являются квадратичными, а хвосты Коши являются логарифмическими.

Экспоненциальные свойства семейства

$B_{\sigma }(\alpha ,\beta )$ образует экспоненциальное семейство с натуральными параметрами $\alpha$ и $\beta$ и достаточная статистика $\log \sigma (x)$ и $\log \sigma (-x)$ . Ожидаемые значения достаточной статистики можно найти путем дифференцирования логарифматора: ^[3]

{\begin{aligned}E[\log \sigma (x)]&={\frac {\partial \log B(\alpha ,\beta )}{\partial \alpha }}=\psi (\alpha )-\psi (\alpha +\beta )\\E[\log \sigma (-x)]&={\frac {\partial \log B(\alpha ,\beta )}{\partial \beta }}=\psi (\beta )-\psi (\alpha +\beta )\\\end{aligned}}

Учитывая набор данных $x_{1},\ldots ,x_{n}$ был сгенерирован предполагается, что IID из $B_{\sigma }(\alpha ,\beta )$ , максимального правдоподобия оценка параметра равна:

{\begin{aligned}{\hat {\alpha }},{\hat {\beta }}=\arg \max _{\alpha ,\beta }&\;{\frac {1}{n}}\sum _{i=1}^{n}\log f(x_{i};\alpha ,\beta )\\=\arg \max _{\alpha ,\beta }&\;\alpha {\Bigl (}{\frac {1}{n}}\sum _{i}\log \sigma (x_{i}){\Bigr )}+\beta {\Bigl (}{\frac {1}{n}}\sum _{i}\log \sigma (-x_{i}){\Bigr )}-\log B(\alpha ,\beta )\\=\arg \max _{\alpha ,\beta }&\;\alpha \,{\overline {\log \sigma (x)}}+\beta \,{\overline {\log \sigma (-x)}}-\log B(\alpha ,\beta )\end{aligned}}

где штриховые линии обозначают средние значения достаточных статистических данных. Оценка максимального правдоподобия зависит от данных только через эту среднюю статистику. Действительно, при оценке максимального правдоподобия ожидаемые значения и средние значения совпадают:

{\begin{aligned}\psi ({\hat {\alpha }})-\psi ({\hat {\alpha }}+{\hat {\beta }})&={\overline {\log \sigma (x)}}\\\psi ({\hat {\beta }})-\psi ({\hat {\alpha }}+{\hat {\beta }})&={\overline {\log \sigma (-x)}}\\\end{aligned}}

где также обращаются в нуль частные производные вышеуказанного максимума.

Отношения с другими дистрибутивами

Отношения с другими дистрибутивами включают:

Логарифмическое отношение гамма-переменных относится к типу IV, как подробно описано выше .
Если $y\sim {\text{BetaPrime}}(\alpha ,\beta )$ , затем $x=\ln y$ имеет распределение IV типа с параметрами $\alpha$ и $\beta$ . См. бета-простое распределение .
Если $z\sim {\text{Gamma}}(\beta ,1)$ и $y\mid z\sim {\text{Gamma}}(\alpha ,z)$ , где $z$ используется как параметр скорости второго гамма-распределения, тогда $y$ имеет сложное гамма-распределение , такое же, как и ${\text{BetaPrime}}(\alpha ,\beta )$ , так что $x=\ln y$ имеет распространение IV типа .
Если $p\sim {\text{Beta}}(\alpha ,\beta )$ , затем $x={\text{logit}}\,p$ имеет распределение IV типа с параметрами $\alpha$ и $\beta$ . См. бета-дистрибутив . Функция логит , $\mathrm {logit} (p)=\log {\frac {p}{1-p}}$ является обратной логистической функцией . Это соотношение объясняет название логистического бета для этого распределения: если логистическая функция применяется к переменным логистического бета, преобразованное распределение является бета.

Большие параметры формы

При больших значениях параметров формы $\alpha ,\beta \gg 1$ , распределение становится более гауссовым , при этом:

{\begin{aligned}E[x]&\approx \ln {\frac {\alpha }{\beta }}\\{\text{var}}[x]&\approx {\frac {\alpha +\beta }{\alpha \beta }}\end{aligned}}

Это показано на графиках в формате pdf и log pdf здесь.

Генерация случайной переменной

Поскольку случайная выборка из гамма- и бета- распределений легко доступна на многих программных платформах, приведенные выше отношения с этими распределениями можно использовать для генерации вариаций из распределения типа IV.

Обобщение с параметрами местоположения и масштаба

Гибкое семейство из четырех параметров можно получить, добавив параметры местоположения и масштаба . Один из способов сделать это — если $x\sim B_{\sigma }(\alpha ,\beta )$ , тогда пусть $y=kx+\delta$ , где $k>0$ является параметром масштаба и $\delta \in \mathbb {R}$ это параметр местоположения. Полученное таким образом семейство из четырех параметров обладает желаемой дополнительной гибкостью, но новые параметры могут быть трудно интерпретировать, поскольку $\delta \neq E[y]$ и $k^{2}\neq {\text{var}}[y]$ . Более того, оценка максимального правдоподобия при такой параметризации затруднена. Эти проблемы можно решить следующим образом.

Напомним, что среднее и дисперсия $x$ являются:

{\begin{aligned}{\tilde {\mu }}&=\psi (\alpha )-\psi (\beta ),&{\tilde {s}}^{2}&=\psi '(\alpha )+\psi '(\beta )\end{aligned}}

Теперь расширьте семейство с помощью параметра местоположения. $\mu \in \mathbb {R}$ и параметр масштабирования $s>0$ , посредством преобразования:

{\begin{aligned}y&=\mu +{\frac {s}{\tilde {s}}}(x-{\tilde {\mu }})\iff x={\tilde {\mu }}+{\frac {\tilde {s}}{s}}(y-\mu )\end{aligned}}

так что $\mu =E[y]$ и $s^{2}={\text{var}}[y]$ теперь интерпретируемы. Можно отметить, что позволяя $s$ быть либо положительным, либо отрицательным не обобщает это семейство из-за вышеупомянутого свойства симметрии . Примем обозначение $y\sim {\bar {B}}_{\sigma }(\alpha ,\beta ,\mu ,s^{2})$ для этой семьи.

Если PDF-файл для $x\sim B_{\sigma }(\alpha ,\beta )$ является $f(x;\alpha ,\beta )$ , затем PDF-файл для $y\sim {\bar {B}}_{\sigma }(\alpha ,\beta ,\mu ,s^{2})$ является:

{\bar {f}}(y;\alpha ,\beta ,\mu ,s^{2})={\frac {\tilde {s}}{s}}\,f(x;\alpha ,\beta )

где это понимается $x$ рассчитывается, как подробно описано выше, как функция $y,\alpha ,\beta ,\mu ,s$ . Приведенные выше графики в формате pdf и log-pdf, где подписи содержат (средние значения = 0, отклонения = 1), предназначены для ${\bar {B}}_{\sigma }(\alpha ,\beta ,0,1)$ .

Оценка параметра максимального правдоподобия

В этом разделе проводится оценка максимального правдоподобия параметров распределения с учетом набора данных. $x_{1},\ldots ,x_{n}$ обсуждается по очереди для семей $B_{\sigma }(\alpha ,\beta )$ и ${\bar {B}}_{\sigma }(\alpha ,\beta ,\mu ,s^{2})$ .

Максимальная вероятность для стандартного типа IV

Как отмечалось выше , $B_{\sigma }(\alpha ,\beta )$ представляет собой экспоненциальное семейство с натуральными параметрами $\alpha ,\beta$ , оценки максимального правдоподобия которых зависят только от усредненной достаточной статистики:

{\begin{aligned}{\overline {\log \sigma (x)}}&={\frac {1}{n}}\sum _{i}\log \sigma (x_{i})&&{\text{and}}&{\overline {\log \sigma (-x)}}&={\frac {1}{n}}\sum _{i}\log \sigma (-x_{i})\end{aligned}}

После накопления этой статистики оценка максимального правдоподобия определяется следующим образом:

{\begin{aligned}{\hat {\alpha }},{\hat {\beta }}=\arg \max _{\alpha ,\beta >0}&\;\alpha \,{\overline {\log \sigma (x)}}+\beta \,{\overline {\log \sigma (-x)}}-\log B(\alpha ,\beta )\end{aligned}}

С помощью параметризации $\theta _{1}=\log \alpha$ и $\theta _{2}=\log \beta$ неограниченный алгоритм численной оптимизации, такой как BFGS можно использовать . Итерации оптимизации выполняются быстро, поскольку они не зависят от размера набора данных.

Альтернативой является использование EM-алгоритма, основанного на композиции: $x-\log(\gamma \delta )\sim B_{\sigma }(\alpha ,\beta )$ если $z\sim {\text{Gamma}}(\beta ,\gamma )$ и $e^{x}\mid z\sim {\text{Gamma}}(\alpha ,z/\delta )$ . Из-за самосопряжения апостериорные гамма-распределения ожидания $\left\langle z\right\rangle _{P(z\mid x)}$ и $\left\langle \log z\right\rangle _{P(z\mid x)}$ которые необходимы для E-шага, можно вычислить в закрытой форме. Обновление параметра M-шага может быть решено аналогично максимальному правдоподобию для гамма-распределения .

Максимальное правдоподобие для семейства с четырьмя параметрами

Задача максимального правдоподобия для ${\bar {B}}_{\sigma }(\alpha ,\beta ,\mu ,s^{2})$ , имея pdf ${\bar {f}}$ является:

{\hat {\alpha }},{\hat {\beta }},{\hat {\mu }},{\hat {s}}=\arg \max _{\alpha ,\beta ,\mu ,s}\log {\frac {1}{n}}\sum _{i}{\bar {f}}(x_{i};\alpha ,\beta ,\mu ,s^{2})

Это больше не экспоненциальное семейство, поэтому каждая итерация оптимизации должна проходить через весь набор данных. Более того, вычисление частных производных (как того требует, например, BFGS) значительно сложнее, чем для вышеупомянутого двухпараметрического случая. Однако все функции компонента легко доступны в пакетах программного обеспечения с автоматической дифференциацией . Опять же, положительные параметры могут быть параметризованы в терминах их логарифмов, чтобы получить задачу неограниченной численной оптимизации.

Для этой задачи численная оптимизация может оказаться неудачной, если исходное местоположение и параметры масштаба не выбраны соответствующим образом. Однако упомянутая выше интерпретируемость этих параметров при параметризации ${\bar {B}}_{\sigma }$ можно использовать для этого. В частности, начальные значения для $\mu$ и $s^{2}$ может быть установлено на эмпирическое среднее значение и дисперсию данных.

См. также

Распределение Чамперноуна , еще одно обобщение логистического распределения.

Ссылки

^ Jump up to: ^а ^б Джонсон, Н.Л., Коц, С., Балакришнан, Н. (1995) Непрерывные одномерные распределения, Том 2 , Wiley. ISBN 0-471-58494-0 (страницы 140–142)
^ Jump up to: ^а ^б Ли Дж. Холливелл (2018). «Лога-гамма-распределение и ненормальная ошибка». S2CID 173176687 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ CMBishop, Распознавание образов и машинное обучение , Springer 2006.

[J1-1] Jump up to: ^а ^б Джонсон, Н.Л., Коц, С., Балакришнан, Н. (1995) Непрерывные одномерные распределения, Том 2 , Wiley. ISBN 0-471-58494-0 (страницы 140–142)

[Haliwell-2] Jump up to: ^а ^б Ли Дж. Холливелл (2018). «Лога-гамма-распределение и ненормальная ошибка». S2CID 173176687 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[3] CMBishop, Распознавание образов и машинное обучение , Springer 2006.

[1]

[2]

[3]