Распространение металога

Трехчленные металогические распределения

Четырехчленное металогическое распределение, когда $a_{3}=0$

Металогическое распределение — это гибкое непрерывное распределение вероятностей, разработанное для простоты использования на практике. Вместе со своими преобразованиями семейство непрерывных распределений металога уникально, поскольку оно воплощает в себе все следующие свойства: практически неограниченную гибкость формы; выбор между неограниченными, полуограниченными и ограниченными распределениями; простота подгонки данных с помощью линейного метода наименьших квадратов; в замкнутой форме простые уравнения функции квантиля (обратный CDF ), которые облегчают моделирование ; простой PDF-файл закрытой формы ; и байесовское обновление в закрытой форме с учетом новых данных. Более того, как и ряд Тейлора , металогические распределения могут иметь любое количество членов, в зависимости от желаемой степени гибкости формы и других потребностей приложения.

Приложения, в которых могут быть полезны металогические распределения, обычно включают в себя подгонку эмпирических данных, смоделированных данных или квантилей , полученных экспертами, для сглаживания, непрерывного распределения вероятностей. Области применения весьма разнообразны и включают экономику, науку, технику и многие другие области. Дистрибутивы металогов, также известные как дистрибутивы Килина, были впервые опубликованы в 2016 году. Том Килин.

История

Историю вероятностных распределений можно частично рассматривать как развитие событий в направлении большей гибкости формы и границ при подгонке к данным . Нормальное распределение было впервые опубликовано в 1756 году. и теорема Байеса в 1763 году. Нормальное распределение заложило основу для большей части развития классической статистики. о состоянии информации, основанных на убеждениях Напротив, теорема Байеса заложила основу для представлений . Поскольку вероятности, основанные на убеждениях, могут принимать любую форму и иметь естественные границы, необходимы были достаточно гибкие распределения вероятностей, чтобы учесть и то, и другое. Более того, многие наборы эмпирических и экспериментальных данных имели формы, которые не могли быть хорошо сопоставлены с нормальным или другими непрерывными распределениями . Так начался поиск непрерывных распределений вероятностей с гибкими формами и границами.

В начале 20 века Пирсон семейство распределений, включающее нормальное , бета , равномерное , гамма , t студента , хи-квадрат , F и пять других, стал крупным достижением в области гибкости формы. За ними последовал Джонсон распределения. Оба семейства могут представлять первые четыре момента данных ( среднее значение , дисперсия , асимметрия и эксцесс ) с помощью плавных непрерывных кривых. Однако они не способны сопоставлять моменты пятого или более высокого порядка. Более того, при заданной асимметрии и эксцессе выбор границ отсутствует. Например, сопоставление первых четырех моментов набора данных может дать распределение с отрицательной нижней границей, даже если известно, что рассматриваемая величина не может быть отрицательной. Наконец, их уравнения включают трудноразрешимые интегралы и сложные статистические функции, поэтому для подбора данных обычно требуются итерационные методы.

В начале 21-го века аналитики принятия решений начали работать над разработкой непрерывных распределений вероятностей, которые точно соответствовали бы любым указанным трем точкам кумулятивной функции распределения для неопределенной величины (например, полученных экспертами $0.10,0.50$, и $0.90$ квантили). Распределения семейств Пирсона и Джонсона, как правило, не подходили для этой цели. Кроме того, аналитики решений также искали распределения вероятностей, которые можно было бы легко параметризовать данными (например, с помощью линейного метода наименьших квадратов или, что то же самое, множественной линейной регрессии ). Представленный в 2011 году класс квантильно-параметризованных распределений (QPD) достиг обеих целей. Хотя по этой причине КПР является значительным достижением, первоначально оно использовалось для иллюстрации этого класса распределений — простое Q-нормальное распределение. имели меньшую гибкость формы, чем семьи Пирсона и Джонсона, и не имели возможности представлять полуограниченные и ограниченные распределения. Вскоре после этого Килин разработало семейство металогических распределений, еще один экземпляр класса QPD, который более гибок по форме, чем семейства Пирсона и Джонсона, предлагает выбор ограниченности, имеет уравнения в замкнутой форме, которые можно подогнать к данным с помощью линейного метода наименьших квадратов, и в закрытой форме имеет квантильные функции , которые облегчают моделирование методом Монте-Карло .

Определение и функция квантиля

Распределение металогов является обобщением логистического распределения , где термин «металог» является сокращением от «металогистический». Начиная с функции логистического квантиля , $x=Q(y)=\mu +s{\mbox{ }}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}$, Килин заменил разложение степенного ряда в кумулятивную вероятность $y=F(x)$ для $\mu$ и $s$ параметры, которые управляют местоположением и масштабом соответственно.

$\mu =a_{1}+a_{4}(y-0.5)+a_{5}(y-0.5)^{2}+a_{7}(y-0.5)^{3}+a_{9}(y-0.5)^{4}+\dots$

$s=a_{2}+a_{3}(y-0.5)+a_{6}(y-0.5)^{2}+a_{8}(y-0.5)^{3}+a_{10}(y-0.5)^{4}+\dots$

Килин обосновал эту замену пятью причинами. Во-первых, результирующая функция квантиля будет иметь значительную гибкость формы, определяемую коэффициентами $a_{i}$. Во-вторых, он будет иметь простую замкнутую форму, линейную по этим коэффициентам, а это означает, что их можно легко определить из CDF данных с помощью линейного метода наименьших квадратов . В-третьих, результирующая функция квантиля будет гладкой, дифференцируемой и аналитической гладкий PDF-файл , гарантируя, что будет доступен в закрытой форме. В-четвертых, моделирование будет облегчено за счет полученного в результате обратного CDF в закрытой форме . В-пятых, как ряд Тейлора , любое количество членов $k$ может использоваться в зависимости от желаемой степени гибкости формы и других потребностей применения.

Обратите внимание, что индексы $a$-коэффициенты таковы, что $a_{1}$ и $a_{4}$ находятся в $\mu$ расширение, $a_{2}$ и $a_{3}$ находятся в $s$ расширение, и после этого индексы чередуются. Такой порядок был выбран таким образом, чтобы первые два члена результирующей металог-квантильной функции точно соответствовали логистическому распределению; добавив третий член с $a_{3}\neq 0$ корректирует асимметрию; добавив четвертый член с $a_{4}\neq 0$ в первую очередь регулирует эксцесс; а добавление последующих ненулевых членов дает более тонкие уточнения формы.

Переписав функцию логистического квантиля, включив в нее указанные выше замены для $\mu$ и $s$ дает металог- квантильную функцию для кумулятивной вероятности $0<y<1$.

$M_{k}(y)=\left\{{\begin{array}{ll}a_{1}+a_{2}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}&{\mbox{for }}k=2\\a_{1}+a_{2}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}+a_{3}(y-0.5)\ln {\Bigl (}{y \over {1-y}}{\Bigr )}&{\mbox{for }}k=3\\a_{1}+a_{2}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}+a_{3}(y-0.5)\ln {\Bigl (}{y \over {1-y}}{\Bigr )}+a_{4}(y-0.5)&{\mbox{for }}k=4\\M_{k-1}(y)+a_{k}(y-0.5)^{k-1 \over 2}&{\mbox{for odd }}k\geq 5\\M_{k-1}(y)+a_{k}(y-0.5)^{{k \over 2}-1}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}&{\mbox{for even }}k\geq 6\\\end{array}}\right.$

Эквивалентно, металог-квантильная функция может быть выражена через базисные функции: $M_{k}(y)=\sum _{i=1}^{k}a_{i}g_{i}(y)$, где металог-базисные функции равны $g_{1}(y)=1,{\mbox{ }}g_{2}(y)=\ln {\Bigl (}{y \over {1-y}}{\Bigr )},$ и каждый последующий $g_{i}(y)$ определяется как выражение, умноженное на $a_{i}$ в уравнении для $M_{k}(y)$ выше. Обратите внимание, что коэффициент $a_{1}$ является медианой , поскольку все остальные члены равны нулю, когда $y=0.5$. Особыми случаями металог-квантильной функции являются логистическое распределение ( $k=2$) и равномерное распределение ( $k\geq 4,a_{1}=0.5,a_{4}=1,a_{i}=0$ в противном случае).

Функция плотности вероятности

Дифференциация $x=M_{k}(y)$ относительно $y$ дает функцию плотности квантиля $q(y)=dx/dy$. обратная этой величине, $(q(y))^{-1}=dy/dx=f(Q(y))$, — функция плотности вероятности, выраженная в виде p-PDF,

$m_{k}(y)=\left\{{\begin{array}{ll}{y(1-y) \over {a_{2}}}&{\mbox{for }}k=2\\{\Bigl (}{a_{2} \over {y(1-y)}}+a_{3}{\Bigl (}{y-0.5 \over {y(1-y)}}+\ln {y \over {1-y}}{\Bigr )}{\Bigr )}^{-1}&{\mbox{for }}k=3\\{\Bigl (}{a_{2} \over {y(1-y)}}+a_{3}{\Bigl (}{y-0.5 \over {y(1-y)}}+\ln {y \over {1-y}}{\Bigr )}+a_{4}{\Bigr )}^{-1}&{\mbox{for }}k=4\\{\Bigl (}{1 \over {m_{k-1}(y)}}+a_{k}{k-1 \over 2}(y-0.5)^{(k-3)/2}{\Bigr )}^{-1}&{\mbox{for odd }}k\geq 5\\{\Bigl (}{1 \over {m_{k-1}(y)}}+a_{k}{\Bigl (}{(y-0.5)^{k/2-1} \over {y(1-y)}}+({k \over 2}-1)(y-0.5)^{(k/2-2)}\ln {y \over {1-y}}{\Bigr )}{\Bigr )}^{-1}&{\mbox{for even }}k\geq 6,\\\end{array}}\right.$

что можно эквивалентно выразить через базисные функции как

$m_{k}(y)=\left(\sum _{i=1}^{k}a_{i}{{dg_{i}(y)} \over {dy}}\right)^{-1}$ где $0<y<1$.

Обратите внимание, что эта PDF выражается как функция кумулятивной вероятности, $y$, а не интересующая переменная, $x$. Чтобы построить PDF-файл (например, как показано на рисунках на этой странице), можно изменить $y\in (0,1)$ параметрически, а затем построить график $x=M_{k}(y)$ по горизонтальной оси и $m_{k}(y)$ на вертикальной оси.

На основе приведенных выше уравнений и следующих преобразований, которые позволяют выбирать границы, семейство распределений металогов состоит из неограниченных, полуограниченных и ограниченных металогов, а также их особых случаев триплета симметричных процентилей (SPT).

Неограниченные, полуограниченные и ограниченные металогические распределения.

Как определено выше, металогическое распределение неограничено, за исключением необычного особого случая, когда $a_{i}=0$ для всех терминов, содержащих $\ln {\Bigl (}{y \over {1-y}}{\Bigr )}$. Однако многие приложения требуют гибких распределений вероятностей, имеющих нижнюю границу. $b_{l}$, верхняя граница $b_{u}$или и то, и другое. Чтобы удовлетворить эту потребность, Килин использовал преобразования для получения полуограниченных и ограниченных металогических распределений. Такие преобразования подчиняются общему свойству функций квантиля: для любой функции квантиля $x=Q(y)$ и повышение функции $z(x),x=z^{-1}(Q(y))$ также является функцией квантиля . Например, функция квантиля нормального распределения равна $x=\mu +\sigma \Phi ^{-1}(y)$; поскольку натуральный логарифм, $z(x)=\ln(x-b_{l})$, — возрастающая функция, $x=b_{l}+e^{\mu +\sigma \Phi ^{-1}(y)}$ — функция квантиля логнормального распределения . Аналогично, применяя это свойство к металогической функции квантиля $M_{k}(y)$ использование приведенных ниже преобразований дает полуограниченные и ограниченные члены семейства металогов. рассматривая $z(x)$ для распространения металогов все члены семейства металогов соответствуют критериям Килина и Паули. определение квантильно-параметризованного распределения и, таким образом, обладать его свойствами.

${\begin{array}{l|c|c|c|c|c}&&&&&{\mbox{shape}}\\&{\mbox{transformation}}&{\mbox{quantile function}}&{\mbox{PDF}}&{\mbox{where}}&{\mbox{parameters}}\\\hline {\mbox{Metalog (unbounded)}}&z(x)=x&M_{k}(y)&m_{k}(y)&0<y<1&k-2\\\hline {\mbox{Log metalog}}&z(x)=\ln(x-b_{l})&M_{k}^{\log(}y)=b_{l}+e^{M_{k}(y)}&m_{k}^{\log(}y)=m_{k}(y)e^{-M_{k}(y)}&0<y<1&k-1\\{\mbox{(bounded below)}}&&=b_{l}&=0&y=0\\\hline {\mbox{Negative-log metalog}}&z(x)=-\ln(b_{u}-x)&M_{k}^{\operatorname {nlog} }(y)=b_{u}-e^{-M_{k}(y)}&m_{k}^{\operatorname {nlog} }(y)=m_{k}(y)e^{M_{k}(y)}&0<y<1&k-1\\{\mbox{(bounded above)}}&&=b_{u}&=0&y=1\\\hline {\mbox{Logit metalog}}&z(x)=\ln {\Bigl (}{x-b_{l} \over {b_{u}-x}}{\Bigr )}&M_{k}^{\operatorname {logit} }(y)={b_{l}+b_{u}e^{M_{k}(y)} \over {1+e^{M_{k}(y)}}}&m_{k}^{\operatorname {logit} }(y)=m_{k}(y){{\bigl (}1+e^{M_{k}(y)}{\bigr )}^{2} \over {(b_{u}-b_{l})e^{M_{k}(y)}}}&0<y<1&k\\{\mbox{(bounded)}}&&=b_{l}&=0&y=0\\&&=b_{u}&=0&y=1\end{array}}$

Обратите внимание, что количество параметров формы в семействе металогов увеличивается линейно с увеличением количества термов. $k$. Следовательно, любой из вышеперечисленных металогов может иметь любое количество параметров формы. Напротив, семейства распределений Пирсона и Джонсона ограничены двумя параметрами формы.

Дистрибутивы металогов SPT

Ограниченный металог SPT, параметризованный данными CDF $(20,0.1),(30,0.5),$ и $(50,0.9)$ и с нижней и верхней границей $0$ и $100$ соответственно.

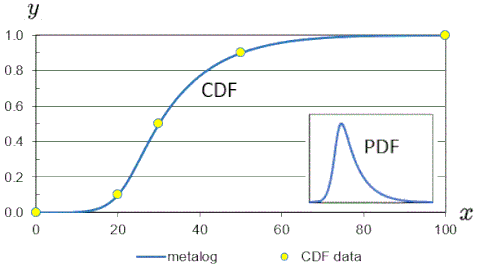
Металоговые распределения симметричных процентилей (SPT) представляют собой трехчленное распределение. $(k=3)$ частный случай неограниченных, полуограниченных и ограниченных металогических распределений. Они параметризуются тремя $(x,y)$ указывает на кривую CDF вида $(x_{1},\alpha )$, $(x_{2},0.5)$, и $(x_{3},1-\alpha )$, где $0<\alpha <0.5$. Металоги SPT полезны, например, когда квантили $(x_{1},x_{2},x_{3})$ соответствующие вероятностям CDF (например, $0.1,0.5,0.9$) извлекаются из эксперта и используются для параметризации трехчленных металогических распределений. Как отмечено ниже, некоторые математические свойства упрощаются параметризацией SPT.

Характеристики

Семейство металогов вероятностных распределений обладает следующими свойствами.

Технико-экономическое обоснование

Функция формы $M_{k}(y)$ или любое из его вышеуказанных преобразований является допустимым распределением вероятностей тогда и только тогда, когда его PDF больше нуля для всех $y\in (0,1).$ Это подразумевает ограничение осуществимости набора коэффициентов ${\boldsymbol {a}}=(a_{1},...,a_{k})\in \mathbb {R} ^{k}$,

$m_{k}(y)>0$ для всех $y\in (0,1)$.

В практических приложениях осуществимость обычно следует проверять, а не предполагать. Для $k=2$, $a_{2}>0$ обеспечивает осуществимость. Для $k=3$ (включая металоги SPT), условие осуществимости $a_{2}>0$ и ${|a_{3}|/a_{2}}<1.66711$. Для $k=4$, была получена аналогичная замкнутая форма. Для $k\geq 5$осуществимость обычно проверяется графически или численно.

Неограниченный металог и его приведенные выше преобразования имеют один и тот же набор допустимых коэффициентов. Следовательно, для заданного набора коэффициентов, подтверждая, что $m_{k}(y)>0$ для всех $y\in (0,1)$ достаточно независимо от используемого преобразования.

Выпуклость

Набор допустимых металог-коэффициентов $S_{\boldsymbol {a}}=\{{\boldsymbol {a}}\in \mathbb {R} ^{k}|m_{k}(y)>0$ для всех $y\in (0,1)\}$ является выпуклым . Поскольку задачи выпуклой оптимизации требуют выпуклых допустимых множеств, это свойство может упростить задачи оптимизации, связанные с металогами. Более того, это свойство гарантирует, что любая выпуклая комбинация ${\boldsymbol {a}}$ допустимы векторы возможных металогов, что полезно, например, при объединении мнений нескольких экспертов. или интерполяция среди возможных металогов. Подразумевается, что любая вероятностная смесь распределений металогов сама по себе является металогом.

Подгонка к данным

Распределение 10-членного металога по максимальной годовой высоте реки (футов) с 1920 по 2014 год для реки Уильямсон ниже впадения реки Спраг, Чилокин, Орегон. Источник данных: Геологическая служба США .

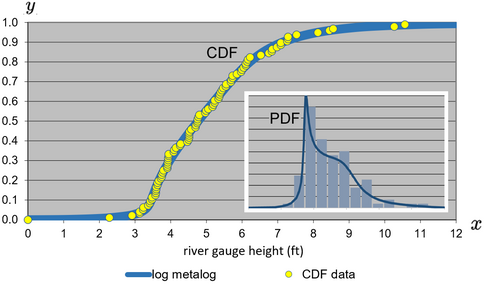
Коэффициенты ${\boldsymbol {a}}$ может быть определена по данным линейным методом наименьших квадратов . Данный $n$ точки данных $(x_{i},y_{i})$ которые предназначены для характеристики металогического CDF, и $n\times k$ матрица ${\boldsymbol {Y}}$ элементы которого состоят из базисных функций $g_{j}(y_{i})$, то пока ${\boldsymbol {Y}}^{T}{\boldsymbol {Y}}$ обратим, вектор-столбец ${\boldsymbol {a}}$ коэффициентов $a_{i}$ дается ${\boldsymbol {a}}=({\boldsymbol {Y}}^{T}{\boldsymbol {Y}})^{-1}{\boldsymbol {Y}}^{T}{\boldsymbol {z}}$, где $n\geq k$ и вектор-столбец ${\boldsymbol {z}}=(z(x_{1}),\ldots ,z(x_{n}))$. Если $n=k$, это уравнение сводится к ${\boldsymbol {a}}={\boldsymbol {Y}}^{-1}{\boldsymbol {z}}$, где результирующий CDF металога проходит точно по всем точкам данных. Для металогов SPT это далее сводится к выражениям в терминах трех $(x_{i},y_{i})$ точки напрямую.

Альтернативный метод аппроксимации, реализованный в виде линейной программы, определяет коэффициенты путем минимизации суммы абсолютных расстояний между CDF и данными с учетом ограничений осуществимости.

Как металоги сходятся к стандартному нормальному распределению как $k$ увеличивается с 2 до 10

Распределения Вейбулла (синие) близко аппроксимируются девятичленными полуограниченными металогическими распределениями (пунктирные, желтые)

Гибкость формы

Согласно теореме металогической гибкости, любое распределение вероятностей с непрерывной функцией квантиля может быть сколь угодно близко аппроксимировано металогом. Более того, в оригинальной статье Килин показал, что десятичленные металогические распределения, параметризованные 105 точками CDF из 30 традиционных исходных распределений (включая нормальное распределение, распределение Стьюдента, логнормальное распределение, гамма-распределение, бета-распределение и распределение экстремальных значений), аппроксимируют каждый такой источник. распределение на расстоянии KS 0,001 или меньше. Таким образом, гибкость формы металога практически неограничена.

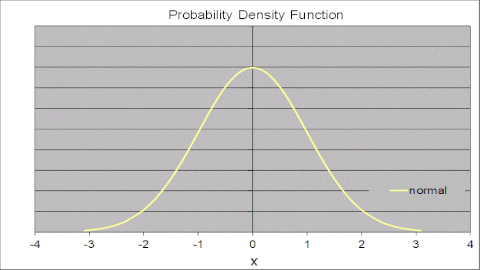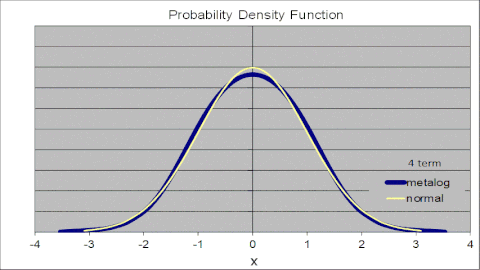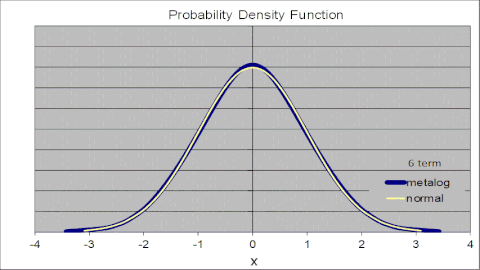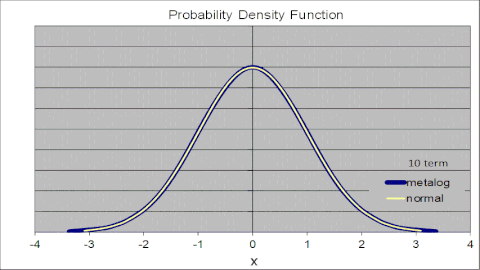
Анимированный рисунок справа иллюстрирует это для стандартного нормального распределения, где металоги с различным количеством термов параметризуются одним и тем же набором из 105 точек из стандартного нормального CDF. Металог PDF сходится к стандартному нормальному PDF по мере увеличения количества терминов. С двумя членами металог аппроксимирует нормальное логистическое распределение. С каждым увеличением количества терминов соответствие становится ближе. Благодаря 10 терминам металог PDF и стандартный обычный PDF визуально неотличимы.

Аналогично, девятичленные полуограниченные металогические PDF-файлы с $b_{l}=0$ визуально неотличимы от ряда распределений Вейбулла . Шесть случаев, показанных справа, соответствуют параметрам формы Вейбулла 0,5, 0,8, 1,0, 1,5, 2 и 4. В каждом случае металог параметризуется девятью $x$ точки из CDF Вейбулла, соответствующие кумулятивным вероятностям $y=(0.001,0.02,0.10,0.25,0.5,0.75,0.9,0.98,0.999)$.

Такая сходимость не является уникальной для нормального распределения и распределения Вейбулла. Килин первоначально показал аналогичные результаты для широкого спектра распределений. и с тех пор предоставил дополнительные иллюстрации.

медиана

Медиана любого распределения в семействе металогов имеет простую замкнутую форму. Обратите внимание, что $y=0.5$ определяет медиану и $M_{k}(0.5)=a_{1}$ (поскольку все последующие члены равны нулю для $y=0.5$). Отсюда следует, что медианы распределений неограниченного металога, логарифмического металога, металога с отрицательным логарифмом и логитного металога равны $a_{1}$, $b_{l}+e^{a_{1}}$, $b_{u}-e^{-a_{1}}$, и ${b_{l}+b_{u}e^{a_{1}} \over {1+e^{a_{1}}}}$, соответственно.

Моменты

The $m^{th}$ момент неограниченного распределения металога, $E[x^{m}]=\int _{y=0}^{1}{M_{k}(y)}^{m}\,dy$, является частным случаем более общей формулы для КФД. Для неограниченного металога такие интегралы оцениваются как моменты замкнутой формы, которые $m^{th}$ полиномы порядка в коэффициентах $a_{i}$. Первые четыре центральных момента четырехчленного неограниченного металога таковы:

${\begin{aligned}{\text{mean}}={}&a_{1}+{a_{3} \over 2}\\[6pt]{\text{variance}}={}&\pi ^{2}{{a_{2}}^{2} \over 3}+{{a_{3}}^{2} \over {12}}+\pi ^{2}{{a_{3}}^{2} \over {36}}+a_{2}a_{4}+{{a_{4}}^{2} \over {12}}\\[6pt]{\text{skewness}}={}&\pi ^{2}{a_{2}}^{2}{a_{3}}+\pi ^{2}{{a_{3}}^{3} \over {24}}+{{{a_{2}}{a_{3}}{a_{4}}} \over {2}}+\pi ^{2}{{{a_{2}}{a_{3}}{a_{4}}} \over {6}}+{{{a_{3}}{a_{4}}^{2}} \over {8}}\\[6pt]{\text{kurtosis}}={}&7\pi ^{4}{{a_{2}}^{4} \over {15}}+3\pi ^{2}{{{a_{2}}^{2}{a_{3}}^{2}} \over {24}}+7\pi ^{4}{{{a_{2}}^{2}{a_{3}}^{2}} \over {30}}+{{{a_{3}}^{4}} \over {80}}+\pi ^{2}{{a_{3}}^{4} \over {24}}+7\pi ^{4}{{a_{3}}^{4} \over {1200}}+2\pi ^{2}{a_{2}}^{3}{a_{4}}\\[6pt]&{}+{{{a_{2}}{a_{3}}^{2}{a_{4}}} \over {2}}+2\pi ^{2}{{{a_{2}}{a_{3}}^{2}{a_{4}}} \over {3}}+2{{a_{2}}^{2}{a_{4}}^{2}}+\pi ^{2}{{{a_{2}}^{2}{a_{4}}^{2}} \over {6}}+{{{a_{3}}^{2}{a_{4}}^{2}} \over {8}}+\pi ^{2}{{{a_{3}}^{2}{a_{4}}^{2}} \over {40}}+{{{a_{2}}{a_{4}}^{3}} \over {3}}+{{a_{4}}^{4} \over {80}}\end{aligned}}$

В эти уравнения включены моменты для меньшего количества членов. Например, моменты трехчленного металога можно получить, полагая $a_{4}$ до нуля. Моменты для металогов с большим количеством членов и моменты более высокого порядка ( $m>4$), также доступны. Моменты для полуограниченных и ограниченных металогов недоступны в закрытой форме.

Параметризация с моментами

Трехчленные неограниченные металоги можно параметризовать в замкнутой форме с помощью первых трех центральных моментов . Позволять $m,v,$ и $s$ — среднее значение, дисперсия и асимметрия, и пусть $s_{s}$ быть стандартизованной асимметрией, $s_{s}=s/v^{3/2}$. Эквивалентные выражения моментов через коэффициенты и коэффициентов через моменты следующие:

${\begin{array}{ll}m=a_{1}+{a_{3} \over 2}&&a_{1}=m-{a_{3} \over 2}\\[6pt]v=\pi ^{2}{{a_{2}}^{2} \over 3}+{{a_{3}}^{2} \over {12}}+\pi ^{2}{{a_{3}}^{2} \over {36}}&&a_{2}={1 \over {\pi }}{\Bigl [}3{\Bigl (}v-{\Bigl (}{1 \over {12}}+{{\pi }^{2} \over {36}}{\Bigr )}{a_{3}}^{2}{\Bigr )}{\Bigr ]}^{1 \over {2}}\\[6pt]s=\pi ^{2}{a_{2}}^{2}{a_{3}}+\pi ^{2}{{a_{3}}^{3} \over {24}}&&a_{3}=4{\Bigl (}{6v \over {6+\pi ^{2}}}{\Bigr )}^{1 \over {2}}\cos {\Bigl [}{1 \over {3}}{\Bigl (}\cos ^{-1}{\Bigl (}-{s_{s} \over {4}}{\Bigl (}1+{{\pi }^{2} \over {6}}{\Bigr )}^{1 \over {2}}{\Bigr )}+4\pi {\Bigr )}{\Bigr ]}\\[6pt]\end{array}}$

Эквивалентность этих двух наборов выражений можно вывести, заметив, что уравнения моментов слева определяют кубический многочлен через коэффициенты $a_{1},a_{2},$ и $a_{3}$, которые можно решить в замкнутом виде как функции $m,v,$ и $s$. Более того, это решение уникально. В терминах моментов условие осуществимости имеет вид $|s_{s}|\leq 2.07093$, что, как можно показать, эквивалентно следующему условию осуществимости с точки зрения коэффициентов: $a_{2}>0$; и ${|a_{3}|/a_{2}}<1.66711$.

Это свойство можно использовать, например, для представления суммы независимых, неидентично распределенных случайных величин . На основе кумулянтов известно, что для любого набора независимых случайных величин среднее значение, дисперсия и асимметрия суммы представляют собой суммы соответствующих средних значений, дисперсий и асимметрий. Параметризация трехчленного металога этими центральными моментами дает непрерывное распределение, которое точно сохраняет эти три момента и, соответственно, обеспечивает разумное приближение к форме распределения суммы независимых случайных величин.

Моделирование

Поскольку их квантильные функции выражены в замкнутой форме, металоги облегчают моделирование методом Монте-Карло . Подставляя равномерно распределенные случайные выборки $y$ в функцию квантиля Metalog (обратный CDF) производит случайные выборки $x$ в закрытой форме, тем самым устраняя необходимость инвертировать CDF. См. ниже приложения для моделирования.

Получение и объединение экспертного мнения

Благодаря своей гибкости формы распределения металогов могут быть привлекательным выбором для получения и представления экспертного мнения. Более того, если мнения нескольких экспертов выражаются как $k$-термовые металоги, консенсусное мнение может быть рассчитано как $k$-терм металог в закрытой форме, где ${\boldsymbol {a}}$-коэффициенты консенсусного металога представляют собой просто средневзвешенное значение коэффициентов отдельных экспертов. Этот результат следует из Винцентизации , где консенсусная функция квантиля представляет собой средневзвешенное значение отдельных функций квантилей.

Байесовское обновление в закрытой форме

В классической статье Говарда (1970) показывает, как бета-биномиальное распределение можно использовать для обновления, согласно правилу Байеса в закрытой форме, неопределенности в отношении долгосрочной частоты. $\phi$ подбрасывания монеты выпадают «орлом» в свете новых данных о подбрасывании монеты. Напротив, если интересующая неопределенность, подлежащая обновлению, определяется не скалярной вероятностью дискретного события (например, результата подбрасывания монеты), а функцией плотности вероятности непрерывной переменной, можно использовать металог-байесовское обновление. При определенных условиях параметры металог-квантиля и ${\boldsymbol {a}}$-коэффициенты могут обновляться в закрытом виде с учетом новых данных согласно правилу Байеса .

Приложения

Для 3474 стальноголовых форелей, пойманных и выпущенных на реке Бабин в Британской Колумбии в 2006–2010 годах, эмпирические данные о весе (гистограмма) и 10-значный логарифмический металог PDF (синяя кривая) соответствуют этим данным методом наименьших квадратов.

Благодаря гибкости формы и границ металоги можно использовать для представления эмпирических или других данных практически в любой области человеческой деятельности.

• Астрономия . Металоги применялись для оценки рисков падения астероида.
• Кибербезопасность . Металоги использовались при оценке рисков кибербезопасности.
• Выявление и объединение экспертных мнений . Статистическое управление Канады получило экспертные мнения о будущих показателях рождаемости в Канаде от 18 экспертов, которые включали использование обратной связи в формате PDF в режиме реального времени на основе электронных таблиц на основе металогов из пяти терминов. Отдельные экспертные мнения затем были взвешены и объединены в общий прогноз на основе металогов.
• Исследование и визуализация эмпирических данных . В биологии рыб 10-членное логарифмическое распределение металога (ограниченное ниже нулевым значением) соответствовало весу 3474 стальных форелей, пойманных и выпущенных на реке Бабин в Британской Колумбии в 2006–2010 годах. Бимодальность полученного распределения объясняется наличием в реке как первых, так и вторых производителей, последние из которых, как правило, весят больше.
• Гидрология . Для моделирования вероятностного распределения годовых высот рек использовался полуограниченный металог из 10 членов.
• Добыча нефти на месторождениях . Полуограниченные металоги SPT использовались для анализа отклонений в прогнозах добычи нефти по сравнению с наблюдаемой добычей постфактум.
• Управление портфелем . Металоги SPT использовались для моделирования коммерческой ценности новых продуктов и портфелей продуктов.
• Распределение входных данных моделирования . Для обоснования решения по тендеру неопределенность относительно будущей стоимости каждого из 259 финансовых активов была представлена ​​в виде металога SPT. Было показано, что моделирование общей стоимости портфеля дает более реалистичные результаты, чем соответствующее моделирование, основанное на дискретных низких, медианных и высоких значениях для каждого актива.
• Распределение результатов моделирования . Металоги также использовались для подбора выходных данных моделирования, чтобы представить эти результаты в виде непрерывных распределений в закрытой форме (как в CDF, так и в PDF). При таком использовании они обычно более стабильны и плавны, чем гистограммы.
• Суммы логнормальных чисел . Металоги позволяют представить в закрытой форме известные дистрибутивы, CDF которых не имеют выражения в закрытой форме. Килин и др. (2019) примените это к сумме независимых одинаково распределенных логнормальных распределений, где квантили суммы могут быть определены с помощью большого количества симуляций. Девять таких квантилей используются для параметризации полуограниченного металогического распределения, которое проходит точно через каждый из этих девяти квантилей. Параметры квантилей хранятся в таблице, которую затем можно интерполировать для получения промежуточных значений; эти значения гарантированно выполнимы благодаря свойству выпуклости, указанному выше.

Панель Metalog для данных о весе стальной головки

Выбор количества терминов

Для данного приложения и набора данных выбор количества металогических терминов $k$ зависит от контекста и может потребовать суждения. Для привлечения экспертов обычно достаточно трех-пяти сроков. Для исследования данных и сопоставления других вероятностных распределений, таких как сумма логнормальных чисел, обычно достаточно восьми-12 членов. Панель металога, на которой отображаются PDF-файлы металога, соответствующие разному количеству терминов. $k$ для данного набора данных может помочь в этом суждении. Например, в металлической панели с грузом Steelhead, использование менее семи терминов, возможно, не соответствует данным, поскольку скрывает присущую им бимодальность. Использование более 11 терминов не является необходимым и в принципе может привести к переобучению данных. Случай с 16 терминами для этого набора данных невозможен, о чем свидетельствует пустая ячейка на панели металога. Другие инструменты, такие как регуляризация и выбор модели ( информационный критерий Акаике и байесовский информационный критерий ), также могут быть полезны. Например, применительно к данным о весе стальной головки рейтинг AIC распределений металогов из 2–16 терминов наряду с широким диапазоном классических распределений определяет металог из 11 терминов как наиболее подходящий для этих данных. Аналогичный рейтинг BIC определяет металог журнала из 10 терминов как наиболее подходящий. Килин (2016) предлагает дальнейшие взгляды на выбор дистрибутива внутри семейства металогов.

Связанные дистрибутивы

Металогические распределения относятся к группе распределений, определяемых с помощью функции квантиля , к которой относятся квантильно-параметризованные распределения , лямбда-распределение Тьюки , его обобщение, GLD, Распределение Говиндараджулу и другие. Следующие дистрибутивы относятся к семейству металогов:

• Логистическое распределение — это частный случай неограниченного металога, где $a_{i}=0$ для всех $i>2$.
• Равномерное распределение является частным случаем: 1) неограниченного металога, где $k\geq 4$, $a_{1}=0.5$, $a_{4}=1$ и $a_{i}=0$ в противном случае; и 2) ограниченный металог, где $k\geq 2$, $b_{l}=0$, $b_{u}=1$, $a_{2}=1$, и $a_{i}=0$ в противном случае.
• , Логарифмическое распределение также известное в экономике как распределение Фиска, представляет собой особый случай логарифмического металога, где $b_{l}=0$, и $a_{i}=0$ для всех $i>2$.
• Логарифмически -равномерное распределение является частным случаем логарифмического металога, где $k\geq 4$, $a_{1}=0.5$, $a_{4}=1$, и $a_{i}=0$ в противном случае.
• Логит-логистическое распределение является частным случаем логит-металога, где $a_{i}=0$ для всех $i>2$.

Программное обеспечение

Для работы с дистрибутивами металога можно использовать свободно доступные программные инструменты:

• Рабочие книги Excel. При вставке или вводе данных CDF мгновенно отображаются металоги (с выбором границ).
  • Рабочая тетрадь металогов SPT вычисляет 2–3 металога термов, определяемых тремя $(x_{i},y_{i})$ Данные CDF.
  • Рабочая тетрадь металогов рассчитывает 2–16 металогов терминов (включая панель металогов), определяемых 2–10 000 $(x_{i},y_{i})$ Данные CDF.
  • ELD (равновероятные данные) Рабочие тетради Metalog рассчитать 2–16 металогов терминов, определяемых 2–10 000 $(x_{i})$ Данные CDF, где $y_{i}$Панели и металоги рассчитываются автоматически.
• Р. рметалог (в Комплексной сети архивов R, CRAN ).
• Питон. Пиметалог близко отражает пакет R. Металогистический использует преимущества платформы SciPy .
• MakeDistribution.com облегчает экспериментирование с металогами, параметризованными несколькими точками данных CDF. Калькулятор металога SPT, металог калькулятор и металогический калькулятор ELD представляют собой онлайн-версии книг Excel.
• Инструменты моделирования SIPmath поддержка распределений металогов в надстройке Excel для моделирования.
• Программное обеспечение Lumina Analytica Free 101 для моделирования и помощи в принятии трудных решений.
• Конструктор металогов BayesFusion позволяет интерактивно создавать дистрибутивы металогов. Genie компании BayesFusion (академическая версия программного обеспечения бесплатна для академических исследований и преподавания) реализует дистрибутивы металогов.

Коммерчески доступные пакеты также поддерживают использование металогических дистрибутивов:

• Решатели FrontLine: аналитический решатель, RASON и Solver SDK, программное обеспечение для оптимизации. Автоматически подбирает пользовательские данные ко всему диапазону металогических распределений (ограниченных и неограниченных, многочленных) и предоставляет возможность сравнивать металогические распределения с классическими распределениями на основе выбранных пользователем критериев согласия.
• Анализ одинокой звезды: программное обеспечение TruNavigator и AnalyticsOS для прогнозной и предписывающей аналитики.

Внешние ссылки

• Веб-сайт Metalog Distributions, www.metalogs.org.
• YouTube-канал Metalog Distributions, обучающие видеоролики