Логистическое распределение

Логистическое распределение

Функция плотности вероятности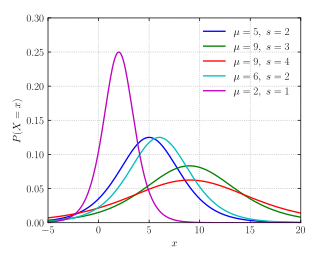
Кумулятивная функция распределения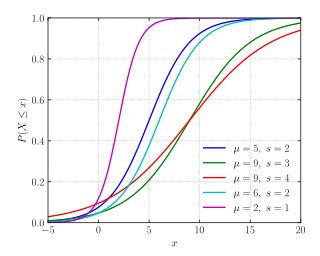
Параметры	$\mu ,$ местоположение ( реальное ) $s>0,$ масштаб (реальный)
Поддерживать	$x\in (-\infty ,\infty )$
PDF	${\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}$
CDF	${\frac {1}{1+e^{-(x-\mu )/s}}}={\frac {1+\tanh {\frac {x-\mu }{2s}}}{2}}$
Квантиль	$\mu +s\log \left({\frac {p}{1-p}}\right)$
Иметь в виду	$\mu$
медиана	$\mu$
Режим	$\mu$
Дисперсия	${\frac {s^{2}\pi ^{2}}{3}}$
асимметрия	$0$
Избыточный эксцесс	$6/5$
Энтропия	$\ln s+2$
МГФ	$e^{\mu t}\mathrm {B} (1-st,1+st)$ для $t\in (-1/s,1/s)$ и $\mathrm {B}$ это бета-функция
CF	$e^{it\mu }{\frac {\pi st}{\sinh(\pi st)}}$
Ожидаемый дефицит	$\mu +{\frac {sH(p)}{1-p}}$ где $H(p)$ это двоичная функция энтропии $H(p)=-p\ln(p)-(1-p)\ln(1-p)$

В теории вероятностей и статистике логистическое распределение представляет собой непрерывное распределение вероятностей . Его кумулятивная функция распределения — это логистическая функция , которая появляется в логистической регрессии и нейронных сетях прямого распространения . По форме оно напоминает нормальное распределение , но имеет более тяжелые хвосты (более высокий эксцесс ). Логистическое распределение является частным случаем лямбда-распределения Тьюки .

Спецификация

Функция плотности вероятности

Когда параметр местоположения μ равен 0, а параметр масштаба s равен 1, тогда функция плотности вероятности логистического распределения определяется выражением

${\begin{aligned}f(x;0,1)&={\frac {e^{-x}}{(1+e^{-x})^{2}}}\\[4pt]&={\frac {1}{(e^{x/2}+e^{-x/2})^{2}}}\\[5pt]&={\frac {1}{4}}\operatorname {sech} ^{2}\left({\frac {x}{2}}\right).\end{aligned}}$

Таким образом, в общем случае плотность равна:

${\begin{aligned}f(x;\mu ,s)&={\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\\[4pt]&={\frac {1}{s\left(e^{(x-\mu )/(2s)}+e^{-(x-\mu )/(2s)}\right)^{2}}}\\[4pt]&={\frac {1}{4s}}\operatorname {sech} ^{2}\left({\frac {x-\mu }{2s}}\right).\end{aligned}}$

Поскольку эту функцию можно выразить через квадрат гиперболической секансной функции «sech», ее иногда называют распределением sech-square(d) . (См. также: гиперболическое секансное распределение ).

Кумулятивная функция распределения

Логистическое распределение получило свое название от своей кумулятивной функции распределения , которая является экземпляром семейства логистических функций. Кумулятивная функция распределения логистического распределения также является масштабированной версией гиперболического тангенса .

$F(x;\mu ,s)={\frac {1}{1+e^{-(x-\mu )/s}}}={\frac {1}{2}}+{\frac {1}{2}}\operatorname {tanh} \left({\frac {x-\mu }{2s}}\right).$

В этом уравнении µ — среднее значение , а s — параметр масштаба, пропорциональный стандартному отклонению .

Квантильная функция

Обратная кумулятивная функция распределения ( функция квантиля ) логистического распределения является обобщением логит- функции. Ее производная называется функцией плотности квантиля. Они определяются следующим образом:

$Q(p;\mu ,s)=\mu +s\ln \left({\frac {p}{1-p}}\right).$

$Q'(p;s)={\frac {s}{p(1-p)}}.$

Альтернативная параметризация

Альтернативную параметризацию логистического распределения можно получить, выразив параметр масштаба: $s$, с точки зрения стандартного отклонения, $\sigma$, используя замену $s\,=\,q\,\sigma$, где $q\,=\,{\sqrt {3}}/{\pi }\,=\,0.551328895\ldots$. Альтернативные формы вышеупомянутых функций достаточно просты.

Приложения

Логистическое распределение — и S-образная структура его кумулятивной функции распределения ( логистическая функция ) и функции квантиля ( логит-функция ) — широко использовались во многих различных областях.

Логистическая регрессия

Одним из наиболее распространенных приложений является логистическая регрессия , которая используется для моделирования категориальных зависимых переменных (например, выбор «да-нет» или выбор из 3 или 4 возможностей), так же, как стандартная линейная регрессия используется для моделирования непрерывных переменных (например, доход или численность населения). В частности, модели логистической регрессии можно сформулировать как скрытых переменных модели , в которых переменные ошибок следуют логистическому распределению. Эта формулировка распространена в теории моделей дискретного выбора , где логистическое распределение играет ту же роль в логистической регрессии, что и нормальное распределение в пробит-регрессии . Действительно, логистическое и нормальное распределения имеют весьма схожую форму. Однако логистическое распределение имеет более тяжелые хвосты , что часто повышает надежность основанного на нем анализа по сравнению с использованием нормального распределения.

Физика

PDF этого распределения имеет ту же функциональную форму, что и производная функции Ферми . В теории свойств электронов в полупроводниках и металлах эта производная устанавливает относительный вес различных энергий электронов в их вкладе в электронный транспорт. Те уровни энергии, энергия которых ближе всего к «среднему» распределению ( уровню Ферми ), доминируют в таких процессах, как электронная проводимость, с некоторым размытием, вызванным температурой. Однако обратите внимание, что соответствующее распределение вероятностей в статистике Ферми – Дирака на самом деле представляет собой простое распределение Бернулли с коэффициентом вероятности, определяемым функцией Ферми.

Логистическое распределение возникает как предельное распределение затухающего случайного движения с конечной скоростью, описываемого телеграфным процессом, в котором случайные моменты времени между последовательными изменениями скорости имеют независимые экспоненциальные распределения с линейно возрастающими параметрами.

Гидрология

Подобрано кумулятивное логистическое распределение октябрьских осадков с использованием CumFreq , см. также Подбор распределения.

В гидрологии распределение долговременного речного стока и осадков (например, месячные и годовые суммы, состоящие из суммы 30 или 360 дневных значений) часто считается почти нормальным в соответствии с центральной предельной теоремой . приближении . Однако нормальное распределение нуждается в числовом Поскольку логистическое распределение, которое можно решить аналитически, похоже на нормальное распределение, его можно использовать вместо него. Синее изображение иллюстрирует пример подгонки логистического распределения к ранжированным октябрьским осадкам, которые распределяются почти нормально, и показывает 90% доверительный интервал, основанный на биномиальном распределении . Данные об осадках представлены в виде координат на графике в рамках кумулятивного частотного анализа .

Шахматные рейтинги

и Федерация шахмат США ФИДЕ переключили свою формулу расчета шахматных рейтингов с нормального распределения на логистическое; см. статью о рейтинговой системе Эло (которая сама основана на нормальном распределении).

Связанные дистрибутивы

• Логистическое распределение имитирует распределение sech .
• Если $X\sim \mathrm {Logistic} (\mu ,s)$ затем $kX+\ell \sim \mathrm {Logistic} (k\mu +\ell ,|k|s)$.
• Если $X\sim$ U(0, 1) тогда $\mu +s(\log X-\log(1-X))\sim \mathrm {Logistic} (\mu ,s)$.
• Если $X\sim \mathrm {Gumbel} (\mu _{X},\beta )$ и $Y\sim \mathrm {Gumbel} (\mu _{Y},\beta )$ тогда независимо $X-Y\sim \mathrm {Logistic} (\mu _{X}-\mu _{Y},\beta )\,$.
• Если $X$ и $Y\sim \mathrm {Gumbel} (\mu ,\beta )$ затем $X+Y\nsim \mathrm {Logistic} (2\mu ,\beta )\,$ (Сумма не является логистическим распределением). Обратите внимание, что $E(X+Y)=2\mu +2\beta \gamma \neq 2\mu =E\left(\mathrm {Logistic} (2\mu ,\beta )\right)$.
• Если X ~ Logistic( , s ) , то exp( X ) ~ LogLogistic $\left(\alpha =e^{\mu },\beta ={\frac {1}{s}}\right)$, и exp( X ) + γ ~ сдвинутый лог-логистический $\left(\alpha =e^{\mu },\beta ={\frac {1}{s}},\gamma \right)$.
• Если X ~ Экспонента (1), то

$\mu +s\log(e^{X}-1)\sim \operatorname {Logistic} (\mu ,s).$

• Если X , Y ~ Экспонента(1), то

$\mu -s\log \left({\frac {X}{Y}}\right)\sim \operatorname {Logistic} (\mu ,s).$

• Металогическое распределение является обобщением логистического распределения, в котором разложение степенного ряда по $p$ заменяются логистическими параметрами $\mu$ и $\sigma$. Полученная металог-квантильная функция обладает высокой гибкостью формы, имеет простую замкнутую форму и может быть адаптирована к данным с помощью линейного метода наименьших квадратов.

Выводы

Моменты высшего порядка

Центральный момент n -го порядка можно выразить через функцию квантиля:

${\begin{aligned}\operatorname {E} [(X-\mu )^{n}]&=\int _{-\infty }^{\infty }(x-\mu )^{n}\,dF(x)\\&=\int _{0}^{1}{\big (}Q(p)-\mu {\big )}^{n}\,dp=s^{n}\int _{0}^{1}\left[\ln \!\left({\frac {p}{1-p}}\right)\right]^{n}\,dp.\end{aligned}}$

Этот интеграл хорошо известен и может быть выражено через числа Бернулли :

$\operatorname {E} [(X-\mu )^{n}]=s^{n}\pi ^{n}(2^{n}-2)\cdot |B_{n}|.$

См. также

• обобщенное логистическое распределение
• Лямбда-распределение Тьюки
• логистика-распределение
• полулогистическое распределение
• логистическая регрессия
• сигмовидная функция

Ссылки

• Джон С. деКани и Роберт А. Стайн (1986). «Заметка о получении информационной матрицы логистического распределения». Американский статистик . 40 . Американская статистическая ассоциация: 220–222. дои : 10.2307/2684541 .
• Н., Балакришнан (1992). Справочник по логистическому распределению . Марсель Деккер, Нью-Йорк. ISBN  0-8247-8587-8 .
• Джонсон, Нидерланды; Коц, С.; Н., Балакришнан (1995). Непрерывные одномерные распределения . Том. 2 (2-е изд.). ISBN  0-471-58494-0 .

• Модис, Теодор (1992) Предсказания: характерные черты общества раскрывают прошлое и предсказывают будущее , Саймон и Шустер, Нью-Йорк. ISBN   0-671-75917-5