Обернутое экспоненциальное распределение

Обернутая экспонента

Функция плотности вероятности 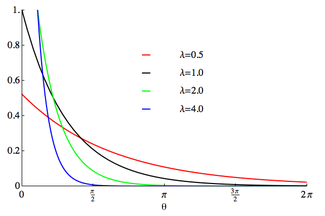Носитель выбран [0,2π]
Кумулятивная функция распределения Носитель выбран [0,2π]
Параметры	$\lambda >0$
Поддерживать	$0\leq \theta <2\pi$
PDF	${\frac {\lambda e^{-\lambda \theta }}{1-e^{-2\pi \lambda }}}$
CDF	${\frac {1-e^{-\lambda \theta }}{1-e^{-2\pi \lambda }}}$
Иметь в виду	$\arctan(1/\lambda )$ (круговой)
Дисперсия	$1-{\frac {\lambda }{\sqrt {1+\lambda ^{2}}}}$ (круговой)
Энтропия	$1+\ln \left({\frac {\beta -1}{\lambda }}\right)-{\frac {\beta }{\beta -1}}\ln(\beta )$ где $\beta =e^{2\pi \lambda }$ (дифференциал)
CF	${\frac {1}{1-in/\lambda }}$

В теории вероятностей и направленной статистике завернутое экспоненциальное распределение — это завернутое распределение вероятностей , которое получается в результате «обертывания» экспоненциального распределения вокруг единичного круга .

Определение

Функция плотности вероятности завернутого экспоненциального распределения равна

$f_{WE}(\theta ;\lambda )=\sum _{k=0}^{\infty }\lambda e^{-\lambda (\theta +2\pi k)}={\frac {\lambda e^{-\lambda \theta }}{1-e^{-2\pi \lambda }}},$

для $0\leq \theta <2\pi$ где $\lambda >0$ — параметр скорости развернутого распределения. Это идентично усеченному распределению, полученному путем ограничения наблюдаемых значений X экспоненциального распределения с параметром скорости λ диапазоном $0\leq X<2\pi$. Обратите внимание, что это распределение не является периодическим.

Характеристическая функция

Характеристическая функция завернутой экспоненты — это просто характеристическая функция экспоненциальной функции, вычисляемой с целочисленными аргументами:

$\varphi _{n}(\lambda )={\frac {1}{1-in/\lambda }}$

что дает альтернативное выражение для завернутой экспоненциальной PDF в терминах круговой переменной z=e ^{я (θ-м)} справедливо для всех действительных θ и m:

${\begin{aligned}f_{WE}(z;\lambda )&={\frac {1}{2\pi }}\sum _{n=-\infty }^{\infty }{\frac {z^{-n}}{1-in/\lambda }}\\[10pt]&={\begin{cases}{\frac {\lambda }{\pi }}\,{\textrm {Im}}(\Phi (z,1,-i\lambda ))-{\frac {1}{2\pi }}&{\text{if }}z\neq 1\\[12pt]{\frac {\lambda }{1-e^{-2\pi \lambda }}}&{\text{if }}z=1\end{cases}}\end{aligned}}$

где $\Phi ()$ – трансцендентная функция Лерха.

Круговые моменты

В терминах круговой переменной $z=e^{i\theta }$ круговые моменты завернутого экспоненциального распределения являются характеристической функцией экспоненциального распределения, оцениваемой с целочисленными аргументами:

$\langle z^{n}\rangle =\int _{\Gamma }e^{in\theta }\,f_{WE}(\theta ;\lambda )\,d\theta ={\frac {1}{1-in/\lambda }},$

где $\Gamma \,$ это некоторый интервал длины $2\pi$. Тогда первый момент представляет собой среднее значение z , также известное как средний результирующий или средний результирующий вектор:

$\langle z\rangle ={\frac {1}{1-i/\lambda }}.$

Средний угол

$\langle \theta \rangle =\mathrm {Arg} \langle z\rangle =\arctan(1/\lambda ),$

а длина среднего результата равна

$R=|\langle z\rangle |={\frac {\lambda }{\sqrt {1+\lambda ^{2}}}}.$

и тогда дисперсия равна 1- R .

Характеристика

Обернутое экспоненциальное распределение представляет собой распределение вероятностей максимальной энтропии для распределений, ограниченных диапазоном $0\leq \theta <2\pi$ при фиксированном значении ожидания $\operatorname {E} (\theta )$.

См. также

• Завернутое распространение
• Направленная статистика