Смещенная логистика-распределение

Сменная логистика

Функция плотности вероятности $\mu =0,\sigma =1,$ ценности $\xi$ как показано в легенде
Кумулятивная функция распределения 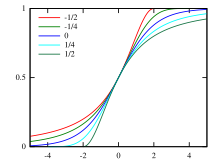$\mu =0,\sigma =1,$ ценности $\xi$ как показано в легенде
Параметры	$\mu \in (-\infty ,+\infty )\,$ местоположение ( реальное ) $\sigma \in (0,+\infty )\,$ масштаб (реальный) $\xi \in (-\infty ,+\infty )\,$ форма (настоящая)
Поддерживать	$x\geqslant \mu -\sigma /\xi \,\;(\xi >0)$ $x\leqslant \mu -\sigma /\xi \,\;(\xi <0)$ $x\in (-\infty ,+\infty )\,\;(\xi =0)$
PDF	${\frac {(1+\xi z)^{-(1/\xi +1)}}{\sigma \left(1+(1+\xi z)^{-1/\xi }\right)^{2}}}$ где $z=(x-\mu )/\sigma \,$
CDF	$\left(1+(1+\xi z)^{-1/\xi }\right)^{-1}\,$ где $z=(x-\mu )/\sigma \,$
Иметь в виду	$\mu +{\frac {\sigma }{\xi }}(\alpha \csc(\alpha )-1)$ где $\alpha =\pi \xi \,$
медиана	$\mu \,$
Режим	$\mu +{\frac {\sigma }{\xi }}\left[\left({\frac {1-\xi }{1+\xi }}\right)^{\xi }-1\right]$
Дисперсия	${\frac {\sigma ^{2}}{\xi ^{2}}}[2\alpha \csc(2\alpha )-(\alpha \csc(\alpha ))^{2}]$ где $\alpha =\pi \xi \,$

Сдвинутое логарифмическое логистическое распределение — это распределение вероятностей, также известное как обобщенное логарифмическое логистическое распределение или логарифмическое логистическое распределение с тремя параметрами. Его также называют обобщенным логистическим распределением. но это противоречит другим значениям этого термина: см. обобщенное логистическое распределение .

Определение

Смещенное логарифмическое логистическое распределение можно получить из логарифмического логистического распределения путем добавления параметра сдвига. $\delta$. Таким образом, если $X$ имеет лог-логистическое распределение, тогда $X+\delta$ имеет смещенное лог-логистическое распределение. Так $Y$ имеет смещенное логарифмически-логистическое распределение, если $\log(Y-\delta )$ имеет логистическое распределение. Параметр сдвига добавляет параметр местоположения к параметрам масштаба и формы (несмещенной) логистики.

Свойства этого распределения легко вывести из свойств логарифмического логистического распределения. Однако альтернативная параметризация, аналогичная той, которая используется для обобщенного распределения Парето и обобщенного распределения экстремальных значений , дает более интерпретируемые параметры, а также помогает их оценке.

В этой параметризации кумулятивная функция распределения (CDF) смещенного логарифмически-логистического распределения равна

$F(x;\mu ,\sigma ,\xi )={\frac {1}{1+\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }}}$

для $1+\xi (x-\mu )/\sigma \geqslant 0$, где $\mu \in \mathbb {R}$ параметр местоположения, $\sigma >0\,$ параметр масштаба и $\xi \in \mathbb {R}$ параметр формы. Обратите внимание, что в некоторых ссылках используется $\kappa =-\xi \,\!$ параметризовать форму.

Функция плотности вероятности (PDF)

$f(x;\mu ,\sigma ,\xi )={\frac {\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-(1/\xi +1)}}{\sigma \left[1+\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }\right]^{2}}},$

опять же, для $1+\xi (x-\mu )/\sigma \geqslant 0.$

Параметр формы $\xi$ часто ограничивается пределами [-1,1], когда функция плотности вероятности ограничена. Когда $|\xi |>1$, оно имеет асимптоту при $x=\mu -\sigma /\xi$. Изменение знака $\xi$ отражает PDF и CDF о $x=\mu .$.

Связанные дистрибутивы

• Когда $\mu =\sigma /\xi ,$ сдвинутая лог-логистика сводится к лог-логистическому распределению.
• Когда $\xi$ → 0, сдвинутая лог-логистика сводится к логистическому распределению .
• Смещенная логистика с параметром формы $\xi =1$ совпадает с обобщенным распределением Парето с параметром формы $\xi =1.$

Приложения

Трехпараметрическое логарифмическое распределение используется в гидрологии для моделирования частоты паводков.

Альтернативная параметризация

Альтернативная параметризация с более простыми выражениями для PDF и CDF выглядит следующим образом. По параметру формы $\alpha$, параметр масштаба $\beta$ и параметр местоположения $\gamma$, PDF-файл имеет вид

$f(x)={\frac {\alpha }{\beta }}{\bigg (}{\frac {x-\gamma }{\beta }}{\bigg )}^{\alpha -1}{\bigg (}1+{\bigg (}{\frac {x-\gamma }{\beta }}{\bigg )}^{\alpha }{\bigg )}^{-2}$

CDF определяется выражением

$F(x)={\bigg (}1+{\bigg (}{\frac {\beta }{x-\gamma }}{\bigg )}^{\alpha }{\bigg )}^{-1}$

Среднее значение $\beta \theta \csc(\theta )+\gamma$ и дисперсия $\beta ^{2}\theta [2\csc(2\theta )-\theta \csc ^{2}(\theta )]$, где $\theta ={\frac {\pi }{\alpha }}$.