Автоматическая дифференциация

В математике и компьютерной алгебре автоматическое дифференцирование ( auto-дифференциация , autodiff или AD ), также называемое алгоритмическим дифференцированием , вычислительным дифференцированием , ^[1]^[2] представляет собой набор методов вычисления частной производной функции, заданной компьютерной программой.

Автоматическое дифференцирование использует тот факт, что каждое компьютерное вычисление, каким бы сложным оно ни было, выполняет последовательность элементарных арифметических операций (сложение, вычитание, умножение, деление и т. д.) и элементарных функций ( exp , log , sin , cos и т. д.). Повторно применяя правило цепочки к этим операциям, частные производные произвольного порядка могут быть вычислены автоматически с точностью до рабочей точности и с использованием не более небольшого постоянного коэффициента большего количества арифметических операций, чем в исходной программе.

Отличие от других методов дифференциации [ править ]

Рисунок 1. Как автоматическая дифференциация связана с символической дифференциацией

Автоматическое дифференцирование отличается от символического дифференцирования и числового дифференцирования . Символьное дифференцирование сталкивается с трудностями преобразования компьютерной программы в одно математическое выражение и может привести к неэффективному коду. Численное дифференцирование (метод конечных разностей) может вносить ошибки округления в процесс дискретизации и отмены. Оба этих классических метода имеют проблемы с вычислением высших производных, где увеличивается сложность и ошибки. Наконец, оба этих классических метода медленны при вычислении частных производных функции по множеству входных данных, что необходимо для градиента на основе алгоритмов оптимизации . Автоматическая дифференциация решает все эти проблемы.

Приложения [ править ]

Автоматическая дифференциация особенно важна в сфере машинного обучения . Например, это позволяет реализовать обратное распространение ошибки в нейронной сети без производной, вычисляемой вручную.

и накопление обратное Прямое

Цепное правило частных производных сложных функций [ править ]

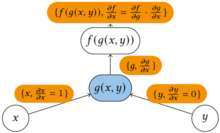
Основой автоматического дифференцирования является разложение дифференциалов, обеспечиваемое цепным правилом частных производных сложных функций . Для простой композиции

{\begin{aligned}y&=f(g(h(x)))=f(g(h(w_{0})))=f(g(w_{1}))=f(w_{2})=w_{3}\\w_{0}&=x\\w_{1}&=h(w_{0})\\w_{2}&=g(w_{1})\\w_{3}&=f(w_{2})=y\end{aligned}}

правило цепочки дает

{\frac {\partial y}{\partial x}}={\frac {\partial y}{\partial w_{2}}}{\frac {\partial w_{2}}{\partial w_{1}}}{\frac {\partial w_{1}}{\partial x}}={\frac {\partial f(w_{2})}{\partial w_{2}}}{\frac {\partial g(w_{1})}{\partial w_{1}}}{\frac {\partial h(w_{0})}{\partial x}}

Два типа автоматического дифференцирования [ править ]

Обычно представлены два различных режима автоматического дифференцирования.

прямое накопление (также называемое восходящим , прямым или касательным режимом )
обратное накопление (также называемое нисходящим , обратным режимом или присоединенным режимом )

Прямое накопление означает, что правило цепочки проходит изнутри наружу (т. е. сначала вычисляется $\partial w_{1}/\partial x$ а потом $\partial w_{2}/\partial w_{1}$ и наконец $\partial y/\partial w_{2}$ ), а обратное накопление имеет обход снаружи внутрь (сначала вычислите $\partial y/\partial w_{2}$ а потом $\partial w_{2}/\partial w_{1}$ и наконец $\partial w_{1}/\partial x$ ). Более кратко,

Прямое накопление вычисляет рекурсивное соотношение: ${\frac {\partial w_{i}}{\partial x}}={\frac {\partial w_{i}}{\partial w_{i-1}}}{\frac {\partial w_{i-1}}{\partial x}}$ с $w_{3}=y$ , и,
Обратное накопление вычисляет рекурсивное соотношение: ${\frac {\partial y}{\partial w_{i}}}={\frac {\partial y}{\partial w_{i+1}}}{\frac {\partial w_{i+1}}{\partial w_{i}}}$ с $w_{0}=x$ .

Значение частной производной, называемой семенем , распространяется вперед или назад и первоначально ${\frac {\partial x}{\partial x}}=1$ или ${\frac {\partial y}{\partial y}}=1$ . Прямое накопление оценивает функцию и вычисляет производную по одной независимой переменной за один проход. Для каждой независимой переменной $x_{1},x_{2},\dots ,x_{n}$ поэтому необходим отдельный проход, в котором производная по этой независимой переменной устанавливается равной единице ( ${\frac {\partial x_{1}}{\partial x_{1}}}=1$ ) и всех остальных к нулю ( ${\frac {\partial x_{2}}{\partial x_{1}}}=\dots ={\frac {\partial x_{n}}{\partial x_{1}}}=0$ ). Напротив, обратное накопление требует оценки частичных функций для частных производных. Поэтому обратное накопление сначала оценивает функцию и вычисляет производные по всем независимым переменным за дополнительный проход.

Какой из этих двух типов следует использовать, зависит от количества разверток. Вычислительная сложность одной проходки пропорциональна сложности исходного кода.

Прямое накопление более эффективно, чем обратное накопление для функций $f : R. н \to Р м$ при $n ≪ m$ только $n$ , поскольку необходимо $проходов по сравнению с m$ проходами для обратного накопления.
Обратное накопление более эффективно, чем прямое накопление для функций $f : R. н \to Р м$ с $n ≫ m$ только $m$ , поскольку необходимо $проходов по сравнению с n$ проходами для прямого накопления.

Обратное распространение ошибок в многослойных персептронах — метод, используемый в машинном обучении , — является частным случаем обратного накопления. ^[2]

Форвардное накопление было введено Р.Э. Венгертом в 1964 году. ^[3] По словам Андреаса Гриванка, обратное накопление предлагалось с конца 1960-х годов, но изобретатель неизвестен. ^[4] Сеппо Линнаинмаа опубликовал обратное накопление в 1976 году. ^[5]

Форвардное накопление [ править ]

При прямом накоплении AD сначала фиксируется независимая переменная , относительно которой выполняется дифференцирование, и вычисляется производная каждого подвыражения рекурсивно . При ручном расчете это включает в себя многократную подстановку производной внутренних функций в цепное правило:

{\begin{aligned}{\frac {\partial y}{\partial x}}&={\frac {\partial y}{\partial w_{n-1}}}{\frac {\partial w_{n-1}}{\partial x}}\\[6pt]&={\frac {\partial y}{\partial w_{n-1}}}\left({\frac {\partial w_{n-1}}{\partial w_{n-2}}}{\frac {\partial w_{n-2}}{\partial x}}\right)\\[6pt]&={\frac {\partial y}{\partial w_{n-1}}}\left({\frac {\partial w_{n-1}}{\partial w_{n-2}}}\left({\frac {\partial w_{n-2}}{\partial w_{n-3}}}{\frac {\partial w_{n-3}}{\partial x}}\right)\right)\\[6pt]&=\cdots \end{aligned}}

Это можно обобщить на несколько переменных как матричное произведение якобианов .

По сравнению с обратным накоплением прямое накопление является естественным и простым в реализации, поскольку поток производной информации совпадает с порядком оценки. Каждая переменная $w_{i}$ дополняется производной ${\dot {w}}_{i}$ (хранится как числовое значение, а не символическое выражение),

{\dot {w}}_{i}={\frac {\partial w_{i}}{\partial x}}

как обозначено точкой. Затем производные вычисляются синхронно с этапами оценки и объединяются с другими производными с помощью правила цепочки.

Используя правило цепочки, если $w_{i}$ имеет предшественников в вычислительном графе:

{\dot {w}}_{i}=\sum _{j\in \{{\text{predecessors of i}}\}}{\frac {\partial w_{i}}{\partial w_{j}}}{\dot {w}}_{j}

Рисунок 2. Пример прямого накопления с вычислительным графом.

В качестве примера рассмотрим функцию:

{\begin{aligned}y&=f(x_{1},x_{2})\\&=x_{1}x_{2}+\sin x_{1}\\&=w_{1}w_{2}+\sin w_{1}\\&=w_{3}+w_{4}\\&=w_{5}\end{aligned}}

Для ясности отдельные подвыражения помечены переменными

w_{i}

.

Выбор независимой переменной, по которой проводится дифференцирование, влияет на начальные значения $ẇ 1$ и $ẇ 2$ . Учитывая интерес к производной этой функции по $x 1$ , начальные значения должны быть установлены следующим образом:

{\begin{aligned}{\dot {w}}_{1}={\frac {\partial w_{1}}{\partial x_{1}}}={\frac {\partial x_{1}}{\partial x_{1}}}=1\\{\dot {w}}_{2}={\frac {\partial w_{2}}{\partial x_{1}}}={\frac {\partial x_{2}}{\partial x_{1}}}=0\end{aligned}}

Если заданы начальные значения, значения распространяются с использованием правила цепочки, как показано. На рис. 2 показано графическое изображение этого процесса в виде вычислительного графа.

Операции по вычислению стоимости	Операции по вычислению производной
$w_{1}=x_{1}$	${\dot {w}}_{1}=1$ (семя)
$w_{2}=x_{2}$	${\dot {w}}_{2}=0$ (семя)
$w_{3}=w_{1}\cdot w_{2}$	${\dot {w}}_{3}=w_{2}\cdot {\dot {w}}_{1}+w_{1}\cdot {\dot {w}}_{2}$
$w_{4}=\sin w_{1}$	${\dot {w}}_{4}=\cos w_{1}\cdot {\dot {w}}_{1}$
$w_{5}=w_{3}+w_{4}$	${\dot {w}}_{5}={\dot {w}}_{3}+{\dot {w}}_{4}$

Чтобы вычислить градиент этой примерной функции, для которой требуется не только ${\tfrac {\partial y}{\partial x_{1}}}$ но и ${\tfrac {\partial y}{\partial x_{2}}}$ , дополнительная проверка выполняется по вычислительному графу с использованием начальных значений ${\dot {w}}_{1}=0;{\dot {w}}_{2}=1$ .

Реализация [ править ]

Псевдокод [ править ]

Прямое накопление вычисляет функцию и производную (но только для одной независимой переменной) за один проход. что выражение Z будет получено относительно переменной V. Связанный вызов метода ожидает , Метод возвращает пару оцениваемой функции и ее производной. Метод рекурсивно обходит дерево выражений до тех пор, пока не будет достигнута переменная. Если запрашивается производная по этой переменной, ее производная равна 1, в противном случае — 0. Затем вычисляются частичная функция и частная производная. ^[6]

tuple<float,float> evaluateAndDerive(Expression Z, Variable V) {
   if isVariable(Z)
      if (Z = V) return {valueOf(Z), 1};
      else return {valueOf(Z), 0};
   else if (Z = A + B)
      {a, a'} = evaluateAndDerive(A, V);
      {b, b'} = evaluateAndDerive(B, V);
      return {a + b, a' + b'};
   else if (Z = A - B)
      {a, a'} = evaluateAndDerive(A, V);
      {b, b'} = evaluateAndDerive(B, V);
      return {a - b, a' - b'};
   else if (Z = A * B)
      {a, a'} = evaluateAndDerive(A, V);
      {b, b'} = evaluateAndDerive(B, V);
      return {a * b, b * a' + a * b'};
}

Питон [ править ]

class ValueAndPartial:
    def __init__(self, value, partial):
        self.value = value
        self.partial = partial

    def toList(self):
        return [self.value, self.partial]

class Expression:
    def __add__(self, other):
        return Plus(self, other)

    def __mul__(self, other):
        return Multiply(self, other)

class Variable(Expression):
    def __init__(self, value):
        self.value = value

    def evaluateAndDerive(self, variable):
        partial = 1 if self == variable else 0
        return ValueAndPartial(self.value, partial)

class Plus(Expression):
    def __init__(self, expressionA, expressionB):
        self.expressionA = expressionA
        self.expressionB = expressionB

    def evaluateAndDerive(self, variable):
        valueA, partialA = self.expressionA.evaluateAndDerive(variable).toList()
        valueB, partialB = self.expressionB.evaluateAndDerive(variable).toList()
        return ValueAndPartial(valueA + valueB, partialA + partialB)

class Multiply(Expression):
    def __init__(self, expressionA, expressionB):
        self.expressionA = expressionA
        self.expressionB = expressionB

    def evaluateAndDerive(self, variable):
        valueA, partialA = self.expressionA.evaluateAndDerive(variable).toList()
        valueB, partialB = self.expressionB.evaluateAndDerive(variable).toList()
        return ValueAndPartial(valueA * valueB, valueB * partialA + valueA * partialB)

# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
x = Variable(2)
y = Variable(3)
z = x * (x + y) + y * y
xPartial = z.evaluateAndDerive(x).partial
yPartial = z.evaluateAndDerive(y).partial
print("∂z/∂x =", xPartial)  # Output: ∂z/∂x = 7
print("∂z/∂y =", yPartial)  # Output: ∂z/∂y = 8

С++ [ править ]

#include <iostream>
struct ValueAndPartial { float value, partial; };
struct Variable;
struct Expression {
   virtual ValueAndPartial evaluateAndDerive(Variable *variable) = 0;
};
struct Variable: public Expression {
   float value;
   Variable(float value): value(value) {}
   ValueAndPartial evaluateAndDerive(Variable *variable) {
      float partial = (this == variable) ? 1.0f : 0.0f;
      return {value, partial};
   }
};
struct Plus: public Expression {
   Expression *a, *b;
   Plus(Expression *a, Expression *b): a(a), b(b) {}
   ValueAndPartial evaluateAndDerive(Variable *variable) {
      auto [valueA, partialA] = a->evaluateAndDerive(variable);
      auto [valueB, partialB] = b->evaluateAndDerive(variable);
      return {valueA + valueB, partialA + partialB};
   }
};
struct Multiply: public Expression {
   Expression *a, *b;
   Multiply(Expression *a, Expression *b): a(a), b(b) {}
   ValueAndPartial evaluateAndDerive(Variable *variable) {
      auto [valueA, partialA] = a->evaluateAndDerive(variable);
      auto [valueB, partialB] = b->evaluateAndDerive(variable);
      return {valueA * valueB, valueB * partialA + valueA * partialB};
   }
};
int main () {
   // Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
   Variable x(2), y(3);
   Plus p1(&x, &y); Multiply m1(&x, &p1); Multiply m2(&y, &y); Plus z(&m1, &m2);
   float xPartial = z.evaluateAndDerive(&x).partial;
   float yPartial = z.evaluateAndDerive(&y).partial;
   std::cout << "∂z/∂x = " << xPartial << ", "
             << "∂z/∂y = " << yPartial << std::endl;
   // Output: ∂z/∂x = 7, ∂z/∂y = 8
   return 0;
}

Обратное накопление [ править ]

При обратном накоплении AD зависимая переменная, которую нужно дифференцировать, фиксируется, а производная вычисляется рекурсивно относительно каждого подвыражения . При бумажном расчете производная внешних функций неоднократно подставляется в цепное правило:

{\begin{aligned}{\frac {\partial y}{\partial x}}&={\frac {\partial y}{\partial w_{1}}}{\frac {\partial w_{1}}{\partial x}}\\&=\left({\frac {\partial y}{\partial w_{2}}}{\frac {\partial w_{2}}{\partial w_{1}}}\right){\frac {\partial w_{1}}{\partial x}}\\&=\left(\left({\frac {\partial y}{\partial w_{3}}}{\frac {\partial w_{3}}{\partial w_{2}}}\right){\frac {\partial w_{2}}{\partial w_{1}}}\right){\frac {\partial w_{1}}{\partial x}}\\&=\cdots \end{aligned}}

При обратном накоплении процентная величина представляет собой сопряженную величину , обозначенную чертой. ${\bar {w}}_{i}$ ; это производная выбранной зависимой переменной по отношению к подвыражению $w_{i}$ :

{\bar {w}}_{i}={\frac {\partial y}{\partial w_{i}}}

Используя правило цепочки, если $w_{i}$ имеет преемников в вычислительном графе:

{\bar {w}}_{i}=\sum _{j\in \{{\text{successors of i}}\}}{\bar {w}}_{j}{\frac {\partial w_{j}}{\partial w_{i}}}

Обратное накопление проходит по цепному правилу снаружи внутрь или, в случае вычислительного графа на рисунке 3, сверху вниз. Пример функции имеет скалярное значение, поэтому для вычисления производной используется только одно начальное значение, и для вычисления (двухкомпонентного) градиента требуется только один проход вычислительного графа. Это только половина работы по сравнению с прямым накоплением, но обратное накопление требует хранения промежуточных переменных $w i,$ а также инструкций, которые их создали, в структуре данных, известной как «лента» или список Венгерта. ^[7] (однако Венгерт опубликовал прямое накопление, а не обратное накопление). ^[3]), что может занимать значительный объем памяти, если вычислительный граф большой. Это можно в некоторой степени смягчить, сохраняя только подмножество промежуточных переменных, а затем реконструируя необходимые рабочие переменные путем повторения оценок - метод, известный как рематериализация . Контрольные точки также используются для сохранения промежуточных состояний.

Рисунок 3: Пример обратного накопления с вычислительным графиком

Операции по вычислению производной с использованием обратного накопления показаны в таблице ниже (обратите внимание на обратный порядок):

Операции по вычислению производной: ${\bar {w}}_{5}=1{\text{ (seed)}}$; ${\bar {w}}_{4}={\bar {w}}_{5}\cdot 1$; ${\bar {w}}_{3}={\bar {w}}_{5}\cdot 1$; ${\bar {w}}_{2}={\bar {w}}_{3}\cdot w_{1}$; ${\bar {w}}_{1}={\bar {w}}_{3}\cdot w_{2}+{\bar {w}}_{4}\cdot \cos w_{1}$

Графиком потока данных вычисления можно манипулировать для расчета градиента исходного расчета. Это делается путем добавления присоединенного узла для каждого основного узла, соединенного присоединенными ребрами, которые параллельны основным ребрам, но текут в противоположном направлении. Узлы сопряженного графа представляют собой умножение на производные функций, рассчитанных узлами простого графа. Например, сложение в первичном элементе приводит к разветвлению в присоединенном; разветвление в первичном вызывает сложение в сопряженном; ^[а] унарная x функция $y = f (в)$ первопричинах $x̄ = ş f'(x)$ в сопряженных; и т. д.

Реализация [ править ]

Псевдокод [ править ]

Обратное накопление требует двух проходов: при прямом проходе сначала вычисляется функция, а частичные результаты кэшируются. При обратном проходе вычисляются частные производные, а полученное ранее значение подвергается обратному распространению. Соответствующий вызов метода ожидает, что выражение Z будет производным и начальным значением будет производное значение родительского выражения. Для верхнего выражения Z, полученного относительно Z, это значение равно 1. Метод рекурсивно обходит дерево выражений до тех пор, пока не будет достигнута переменная, и добавляет текущее начальное значение к производному выражению. ^[8]^[9]

void derive(Expression Z, float seed) {
   if isVariable(Z)
      partialDerivativeOf(Z) += seed;
   else if (Z = A + B)
      derive(A, seed);
      derive(B, seed);
   else if (Z = A - B)
      derive(A, seed);
      derive(B, -seed);
   else if (Z = A * B)
      derive(A, valueOf(B) * seed);
      derive(B, valueOf(A) * seed);
}

Питон [ править ]

class Expression:
    def __add__(self, other):
        return Plus(self, other)
    def __mul__(self, other):
        return Multiply(self, other)

class Variable(Expression):
    def __init__(self, value):
        self.value = value
        self.partial = 0

    def evaluate(self):
        pass

    def derive(self, seed):
        self.partial += seed

class Plus(Expression):
    def __init__(self, expressionA, expressionB):
        self.expressionA = expressionA
        self.expressionB = expressionB
        self.value = None

    def evaluate(self):
        self.expressionA.evaluate()
        self.expressionB.evaluate()
        self.value = self.expressionA.value + self.expressionB.value

    def derive(self, seed):
        self.expressionA.derive(seed)
        self.expressionB.derive(seed)

class Multiply(Expression):
    def __init__(self, expressionA, expressionB):
        self.expressionA = expressionA
        self.expressionB = expressionB
        self.value = None

    def evaluate(self):
        self.expressionA.evaluate()
        self.expressionB.evaluate()
        self.value = self.expressionA.value * self.expressionB.value

    def derive(self, seed):
        self.expressionA.derive(self.expressionB.value * seed)
        self.expressionB.derive(self.expressionA.value * seed)

# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
x = Variable(2)
y = Variable(3)
z = x * (x + y) + y * y
z.evaluate()
print("z =", z.value)        # Output: z = 19
z.derive(1)
print("∂z/∂x =", x.partial)  # Output: ∂z/∂x = 7
print("∂z/∂y =", y.partial)  # Output: ∂z/∂y = 8

С++ [ править ]

#include <iostream>
struct Expression {
   float value;
   virtual void evaluate() = 0;
   virtual void derive(float seed) = 0;
};
struct Variable: public Expression {
   float partial;
   Variable(float _value) {
      value = _value;
      partial = 0;
   }
   void evaluate() {}
   void derive(float seed) {
      partial += seed;
   }
};
struct Plus: public Expression {
   Expression *a, *b;
   Plus(Expression *a, Expression *b): a(a), b(b) {}
   void evaluate() {
      a->evaluate();
      b->evaluate();
      value = a->value + b->value;
   }
   void derive(float seed) {
      a->derive(seed);
      b->derive(seed);
   }
};
struct Multiply: public Expression {
   Expression *a, *b;
   Multiply(Expression *a, Expression *b): a(a), b(b) {}
   void evaluate() {
      a->evaluate();
      b->evaluate();
      value = a->value * b->value;
   }
   void derive(float seed) {
      a->derive(b->value * seed);
      b->derive(a->value * seed);
   }
};
int main () {
   // Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
   Variable x(2), y(3);
   Plus p1(&x, &y); Multiply m1(&x, &p1); Multiply m2(&y, &y); Plus z(&m1, &m2);
   z.evaluate();
   std::cout << "z = " << z.value << std::endl;
   // Output: z = 19
   z.derive(1);
   std::cout << "∂z/∂x = " << x.partial << ", "
             << "∂z/∂y = " << y.partial << std::endl;
   // Output: ∂z/∂x = 7, ∂z/∂y = 8
   return 0;
}

прямого и накопления Помимо обратного

Прямое и обратное накопление — это всего лишь два (крайних) способа обойти правило цепочки. Проблема вычисления полного якобиана $f : R н \to Р м$ с минимальным количеством арифметических операций, известна как задача оптимального накопления якобиана (OJA), которая является NP-полной . ^[10] Центральным элементом этого доказательства является идея о том, что между локальными партиалами, обозначающими ребра графа, могут существовать алгебраические зависимости. В частности, две или более метки ребер могут быть признаны равными. Сложность проблемы остается открытой, если предположить, что все метки ребер уникальны и алгебраически независимы.

Автоматическое дифференцирование с двойных чисел использованием

Автоматическое дифференцирование в прямом режиме осуществляется путем расширения алгебры действительных чисел и получения новой арифметики . К каждому числу добавляется дополнительный компонент, представляющий производную функции по этому числу, а все арифметические операторы расширяются для расширенной алгебры. Расширенная алгебра — это алгебра двойственных чисел .

Заменить каждую цифру $\,x$ с номером $x+x'\varepsilon$ , где $x'$ это действительное число, но $\varepsilon$ — абстрактное число со свойством $\varepsilon ^{2}=0$ ( бесконечно малый ; см. Гладкий бесконечно малый анализ ). Используя только это, обычная арифметика дает

{\begin{aligned}(x+x'\varepsilon )+(y+y'\varepsilon )&=x+y+(x'+y')\varepsilon \\(x+x'\varepsilon )-(y+y'\varepsilon )&=x-y+(x'-y')\varepsilon \\(x+x'\varepsilon )\cdot (y+y'\varepsilon )&=xy+xy'\varepsilon +yx'\varepsilon +x'y'\varepsilon ^{2}=xy+(xy'+yx')\varepsilon \\(x+x'\varepsilon )/(y+y'\varepsilon )&=(x/y+x'\varepsilon /y)/(1+y'\varepsilon /y)=(x/y+x'\varepsilon /y)\cdot (1-y'\varepsilon /y)=x/y+(x'/y-xy'/y^{2})\varepsilon \end{aligned}}

с использованием

(1+y'\varepsilon /y)\cdot (1-y'\varepsilon /y)=1

.

Теперь полиномы можно вычислять с помощью этой расширенной арифметики. Если $P(x)=p_{0}+p_{1}x+p_{2}x^{2}+\cdots +p_{n}x^{n}$ , затем

{\begin{aligned}P(x+x'\varepsilon )&=p_{0}+p_{1}(x+x'\varepsilon )+\cdots +p_{n}(x+x'\varepsilon )^{n}\\&=p_{0}+p_{1}x+\cdots +p_{n}x^{n}+p_{1}x'\varepsilon +2p_{2}xx'\varepsilon +\cdots +np_{n}x^{n-1}x'\varepsilon \\&=P(x)+P^{(1)}(x)x'\varepsilon \end{aligned}}

где

P^{(1)}

обозначает производную

P

относительно его первого аргумента, и

x'

, называемое начальным числом , может быть выбрано произвольно.

Новая арифметика состоит из упорядоченных пар элементов, записанных $\langle x,x'\rangle$ , с обычной арифметикой для первого компонента и арифметикой дифференцирования первого порядка для второго компонента, как описано выше. Распространение приведенных выше результатов о полиномах на аналитические функции дает список базовой арифметики и некоторых стандартных функций для новой арифметики:

{\begin{aligned}\left\langle u,u'\right\rangle +\left\langle v,v'\right\rangle &=\left\langle u+v,u'+v'\right\rangle \\\left\langle u,u'\right\rangle -\left\langle v,v'\right\rangle &=\left\langle u-v,u'-v'\right\rangle \\\left\langle u,u'\right\rangle *\left\langle v,v'\right\rangle &=\left\langle uv,u'v+uv'\right\rangle \\\left\langle u,u'\right\rangle /\left\langle v,v'\right\rangle &=\left\langle {\frac {u}{v}},{\frac {u'v-uv'}{v^{2}}}\right\rangle \quad (v\neq 0)\\\sin \left\langle u,u'\right\rangle &=\left\langle \sin(u),u'\cos(u)\right\rangle \\\cos \left\langle u,u'\right\rangle &=\left\langle \cos(u),-u'\sin(u)\right\rangle \\\exp \left\langle u,u'\right\rangle &=\left\langle \exp u,u'\exp u\right\rangle \\\log \left\langle u,u'\right\rangle &=\left\langle \log(u),u'/u\right\rangle \quad (u>0)\\\left\langle u,u'\right\rangle ^{k}&=\left\langle u^{k},u'ku^{k-1}\right\rangle \quad (u\neq 0)\\\left|\left\langle u,u'\right\rangle \right|&=\left\langle \left|u\right|,u'\operatorname {sign} u\right\rangle \quad (u\neq 0)\end{aligned}}

и вообще для примитивной функции

g

,

g(\langle u,u'\rangle ,\langle v,v'\rangle )=\langle g(u,v),g_{u}(u,v)u'+g_{v}(u,v)v'\rangle

где

g_{u}

и

g_{v}

являются производными от

g

относительно его первого и второго аргументов соответственно.

Когда к смешанным аргументам применяется базовая двоичная арифметическая операция — пара $\langle u,u'\rangle$ и реальное число $c$ — действительное число сначала увеличивается до $\langle c,0\rangle$ . Производная функции $f:\mathbb {R} \to \mathbb {R}$ в точку $x_{0}$ теперь находится путем вычисления $f(\langle x_{0},1\rangle )$ используя приведенную выше арифметику, которая дает $\langle f(x_{0}),f'(x_{0})\rangle$ как результат.

Реализация [ править ]

Ниже приведен пример реализации, основанной на подходе двойного числа.

Псевдокод [ править ]

Dual plus(Dual A, Dual B) {
  return {
    realPartOf(A) + realPartOf(B),
    infinitesimalPartOf(A) + infinitesimalPartOf(B)
  };
}
Dual minus(Dual A, Dual B) {
  return {
    realPartOf(A) - realPartOf(B),
    infinitesimalPartOf(A) - infinitesimalPartOf(B)
  };
}
Dual multiply(Dual A, Dual B) {
  return {
    realPartOf(A) * realPartOf(B),
    realPartOf(B) * infinitesimalPartOf(A) + realPartOf(A) * infinitesimalPartOf(B)
  };
}
X = {x, 0};
Y = {y, 0};
Epsilon = {0, 1};
xPartial = infinitesimalPartOf(f(X + Epsilon, Y));
yPartial = infinitesimalPartOf(f(X, Y + Epsilon));

Питон [ править ]

class Dual:
    def __init__(self, realPart, infinitesimalPart=0):
        self.realPart = realPart
        self.infinitesimalPart = infinitesimalPart

    def __add__(self, other):
        return Dual(
            self.realPart + other.realPart,
            self.infinitesimalPart + other.infinitesimalPart
        )

    def __mul__(self, other):
        return Dual(
            self.realPart * other.realPart,
            other.realPart * self.infinitesimalPart + self.realPart * other.infinitesimalPart
        )

# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
def f(x, y):
    return x * (x + y) + y * y
x = Dual(2)
y = Dual(3)
epsilon = Dual(0, 1)
a = f(x + epsilon, y)
b = f(x, y + epsilon)
print("∂z/∂x =", a.infinitesimalPart)  # Output: ∂z/∂x = 7
print("∂z/∂y =", b.infinitesimalPart)  # Output: ∂z/∂y = 8

С++ [ править ]

#include <iostream>
struct Dual {
   float realPart, infinitesimalPart;
   Dual(float realPart, float infinitesimalPart=0): realPart(realPart), infinitesimalPart(infinitesimalPart) {}
   Dual operator+(Dual other) {
      return Dual(
         realPart + other.realPart,
         infinitesimalPart + other.infinitesimalPart
      );
   }
   Dual operator*(Dual other) {
      return Dual(
         realPart * other.realPart,
         other.realPart * infinitesimalPart + realPart * other.infinitesimalPart
      );
   }
};
// Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
Dual f(Dual x, Dual y) { return x * (x + y) + y * y; }
int main () {
   Dual x = Dual(2);
   Dual y = Dual(3);
   Dual epsilon = Dual(0, 1);
   Dual a = f(x + epsilon, y);
   Dual b = f(x, y + epsilon);
   std::cout << "∂z/∂x = " << a.infinitesimalPart << ", "
             << "∂z/∂y = " << b.infinitesimalPart << std::endl;
   // Output: ∂z/∂x = 7, ∂z/∂y = 8
   return 0;
}

Векторные аргументы и функции [ править ]

Многомерные функции можно обрабатывать с той же эффективностью и механизмами, что и одномерные функции, используя оператор производной по направлению. То есть, если достаточно вычислить $y'=\nabla f(x)\cdot x'$ , производная по направлению $y'\in \mathbb {R} ^{m}$ из $f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ в $x\in \mathbb {R} ^{n}$ в направлении $x'\in \mathbb {R} ^{n}$ может быть рассчитано как $(\langle y_{1},y'_{1}\rangle ,\ldots ,\langle y_{m},y'_{m}\rangle )=f(\langle x_{1},x'_{1}\rangle ,\ldots ,\langle x_{n},x'_{n}\rangle )$ используя ту же арифметику, что и выше. Если все элементы $\nabla f$ желательны, то $n$ необходимы функциональные оценки. Обратите внимание, что во многих приложениях оптимизации производная по направлению действительно достаточна.

Высокий порядок и множество переменных [ править ]

Приведенную выше арифметику можно обобщить для расчета производных второго порядка и более высоких функций многомерных функций. Однако арифметические правила быстро усложняются: сложность квадратична в высшей степени производной. усеченную алгебру полиномов Тейлора Вместо этого можно использовать . Получающаяся в результате арифметика, определенная на обобщенных двойственных числах, позволяет эффективно выполнять вычисления с использованием функций, как если бы они были типом данных. Если известен полином Тейлора функции, производные легко извлекаются.

Реализация [ править ]

AD в прямом режиме реализуется посредством нестандартной интерпретации программы, в которой действительные числа заменяются двойными числами, константы преобразуются в двойные числа с нулевым эпсилон-коэффициентом, а числовые примитивы повышаются для работы с двойственными числами. Эта нестандартная интерпретация обычно реализуется с использованием одной из двух стратегий: преобразования исходного кода или перегрузки операторов .

Трансформация исходного кода (SCT) [ править ]

Рисунок 4. Пример того, как может работать преобразование исходного кода.

Исходный код функции заменяется автоматически сгенерированным исходным кодом, который включает операторы для вычисления производных, чередующиеся с исходными инструкциями.

Преобразование исходного кода может быть реализовано для всех языков программирования, и компилятору также легче выполнять оптимизацию времени компиляции. Однако реализация самого инструмента AD более сложна, а система сборки более сложна.

Перегрузка операторов (ОО) [ править ]

Рисунок 5. Пример того, как может работать перегрузка операторов.

Перегрузка операторов возможна для исходного кода, написанного на поддерживающем ее языке. Объекты для действительных чисел и элементарных математических операций должны быть перегружены, чтобы обеспечить расширенную арифметику, описанную выше. Это не требует изменения формы или последовательности операций в исходном исходном коде для дифференциации функции, но часто требует изменений в базовых типах данных для чисел и векторов для поддержки перегрузки и часто также включает в себя вставку специальных операций пометки. Из-за присущих каждому циклу накладных расходов на перегрузку операторов этот подход обычно демонстрирует более низкую производительность по скорости.

Перегрузка операторов и преобразование исходного кода [ править ]

Перегруженные операторы можно использовать для извлечения графика оценки с последующим автоматическим созданием AD-версии основной функции во время выполнения. В отличие от классического ОО ААД, такая AD-функция не меняется от одной итерации к следующей. Следовательно, для каждой выборки Xi возникают какие-либо накладные расходы во время выполнения объектно-ориентированной интерпретации или интерпретации ленты.

Поскольку AD-функция генерируется во время выполнения, ее можно оптимизировать, чтобы учесть текущее состояние программы и предварительно вычислить определенные значения. Кроме того, его можно сгенерировать таким образом, чтобы последовательно использовать встроенную векторизацию ЦП для обработки 4(8)-двойных фрагментов пользовательских данных (ускорение AVX2\AVX512 x4-x8). С учетом многопоточности такой подход может привести к окончательному ускорению порядка 8 × #Cores по сравнению с традиционными инструментами AAD. Эталонная реализация доступна на GitHub. ^[11]

См. также [ править ]

Дифференцируемое программирование

Примечания [ править ]

^ С точки зрения весовых матриц сопряженным является транспонирование . Сложение – это ковектор $[1\cdots 1]$ , с $[1\cdots 1]\left[{\begin{smallmatrix}x_{1}\\\vdots \\x_{n}\end{smallmatrix}}\right]=x_{1}+\cdots +x_{n},$ и разветвление - это вектор $\left[{\begin{smallmatrix}1\\\vdots \\1\end{smallmatrix}}\right],$ с $\left[{\begin{smallmatrix}1\\\vdots \\1\end{smallmatrix}}\right][x]=\left[{\begin{smallmatrix}x\\\vdots \\x\end{smallmatrix}}\right].$

Ссылки [ править ]

^ Найдингер, Ричард Д. (2010). «Введение в автоматическое дифференцирование и объектно-ориентированное программирование MATLAB» (PDF) . Обзор СИАМ . 52 (3): 545–563. CiteSeerX 10.1.1.362.6580 . дои : 10.1137/080743627 . S2CID 17134969 .
^ Jump up to: Перейти обратно: ^а ^б Байдин, Атилим Гюнес; Перлмуттер, Барак; Радуль Алексей Андреевич; Сискинд, Джеффри (2018). «Автоматическая дифференциация в машинном обучении: опрос» . Журнал исследований машинного обучения . 18 : 1–43.
^ Jump up to: Перейти обратно: ^а ^б Р.Э. Венгерт (1964). «Простая автоматическая программа оценки производных» . Комм. АКМ . 7 (8): 463–464. дои : 10.1145/355586.364791 . S2CID 24039274 .
^ Гриванк, Андреас (2012). «Кто изобрел обратный способ дифференциации?» (PDF) . Истории оптимизации, Documenta Matematica . Дополнительный том ISMP: 389–400. дои : 10.4171/dms/6/38 . ISBN 978-3-936609-58-5 .
^ Линнаинмаа, Сеппо (1976). «Разложение Тейлора накопленной ошибки округления». БИТ Численная математика . 16 (2): 146–160. дои : 10.1007/BF01931367 . S2CID 122357351 .
^ Максимилиан Э. Шюле, Максимилиан Шпрингер, Альфонс Кемпер , Томас Нойманн (2022). «Оптимизация кода LLVM для автоматического дифференцирования». Материалы шестого семинара по управлению данными для сквозного машинного обучения . стр. 1–4. дои : 10.1145/3533028.3533302 . ISBN 9781450393751 . S2CID 248853034 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Бартоломью-Биггс, Майкл; Браун, Стивен; Кристиансон, Брюс; Диксон, Лоуренс (2000). «Автоматическое дифференцирование алгоритмов». Журнал вычислительной и прикладной математики . 124 (1–2): 171–190. Бибкод : 2000JCoAM.124..171B . дои : 10.1016/S0377-0427(00)00422-2 . hdl : 2299/3010 .
^ Максимилиан Э. Шюле, Харальд Ланг, Максимилиан Шпрингер, Альфонс Кемпер , Томас Нойманн , Стефан Гюннеманн (2021). «Машинное обучение в базе данных с использованием SQL на графических процессорах». 33-я Международная конференция по управлению научными и статистическими базами данных . стр. 25–36. дои : 10.1145/3468791.3468840 . ISBN 9781450384131 . S2CID 235386969 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Максимилиан Э. Шюле, Харальд Ланг, Максимилиан Шпрингер, Альфонс Кемпер , Томас Нойманн , Стефан Гюннеманн (2022). «Рекурсивный SQL и поддержка графических процессоров для машинного обучения в базе данных» . Распределенные и параллельные базы данных . 40 (2–3): 205–259. дои : 10.1007/s10619-022-07417-7 . S2CID 250412395 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Науманн, Уве (апрель 2008 г.). «Оптимальное накопление якобиана NP-полное». Математическое программирование . 112 (2): 427–441. CiteSeerX 10.1.1.320.5665 . дои : 10.1007/s10107-006-0042-z . S2CID 30219572 .
^ «Библиотека прототипов AADC» . 22 июня 2022 г. – через GitHub.

Дальнейшее чтение [ править ]

Ралл, Луи Б. (1981). Автоматическая дифференциация: методы и приложения . Конспекты лекций по информатике. Том. 120. Спрингер . ISBN 978-3-540-10861-0 .
Гриванк, Андреас; Вальтер, Андреа (2008). Оценка производных: принципы и методы алгоритмического дифференцирования . Другие названия по прикладной математике. Том. 105 (2-е изд.). СИАМ . дои : 10.1137/1.9780898717761 . ISBN 978-0-89871-659-7 .
Найдингер, Ричард (2010). «Введение в автоматическое дифференцирование и объектно-ориентированное программирование MATLAB» (PDF) . Обзор СИАМ . 52 (3): 545–563. CiteSeerX 10.1.1.362.6580 . дои : 10.1137/080743627 . S2CID 17134969 . Проверено 15 марта 2013 г.
Науманн, Уве (2012). Искусство дифференциации компьютерных программ . Программное обеспечение-Среда-инструменты. СИАМ . ISBN 978-1-611972-06-1 .
Хенрард, Марк (2017). Объяснение алгоритмической дифференциации в финансах . Объяснение финансовой инженерии. Пэлгрейв Макмиллан . ISBN 978-3-319-53978-2 .

Внешние ссылки [ править ]

www.autodiff.org , «начальный сайт со всем, что вы хотите знать об автоматической дифференциации».
Автоматическое дифференцирование параллельных программ OpenMP
Автоматическое дифференцирование, шаблоны C++ и фотограмметрия
Автоматическая дифференциация, подход с перегрузкой оператора
Вычисление аналитических производных любой программы на Fortran77, Fortran95 или C через веб-интерфейс. Автоматическое дифференцирование программ на Fortran.
Описание и пример кода для прямой автоматической дифференциации в Scala. Архивировано 3 августа 2016 г. на Wayback Machine.
finmath-lib стохастическое автоматическое дифференцирование , Автоматическое дифференцирование для случайных величин (Java-реализация стохастического автоматического дифференцирования).
Сопряженное алгоритмическое дифференцирование: калибровка и теорема о неявной функции
автоматического дифференцирования на основе шаблонов C++ Статья и реализация
Касательные отлаживаемые производные от источника к источнику
Точные греки первого и второго порядка путем алгоритмического дифференцирования
Сопряженное алгоритмическое дифференцирование приложения с ускорением на графическом процессоре
Сопряженные методы в вычислительных финансах. Программная поддержка алгоритмического дифференцирования.
Увеличение скорости расчета цен xVA более чем в тысячу раз с помощью масштабируемых процессоров Intel Xeon

[8] С точки зрения весовых матриц сопряженным является транспонирование . Сложение – это ковектор $[1\cdots 1]$ , с $[1\cdots 1]\left[{\begin{smallmatrix}x_{1}\\\vdots \\x_{n}\end{smallmatrix}}\right]=x_{1}+\cdots +x_{n},$ и разветвление - это вектор $\left[{\begin{smallmatrix}1\\\vdots \\1\end{smallmatrix}}\right],$ с $\left[{\begin{smallmatrix}1\\\vdots \\1\end{smallmatrix}}\right][x]=\left[{\begin{smallmatrix}x\\\vdots \\x\end{smallmatrix}}\right].$

[1] Найдингер, Ричард Д. (2010). «Введение в автоматическое дифференцирование и объектно-ориентированное программирование MATLAB» (PDF) . Обзор СИАМ . 52 (3): 545–563. CiteSeerX 10.1.1.362.6580 . дои : 10.1137/080743627 . S2CID 17134969 .

[baydin2018automatic-2] Jump up to: Перейти обратно: ^а ^б Байдин, Атилим Гюнес; Перлмуттер, Барак; Радуль Алексей Андреевич; Сискинд, Джеффри (2018). «Автоматическая дифференциация в машинном обучении: опрос» . Журнал исследований машинного обучения . 18 : 1–43.

[Wengert1964-3] Jump up to: Перейти обратно: ^а ^б Р.Э. Венгерт (1964). «Простая автоматическая программа оценки производных» . Комм. АКМ . 7 (8): 463–464. дои : 10.1145/355586.364791 . S2CID 24039274 .

[grie2012-4] Гриванк, Андреас (2012). «Кто изобрел обратный способ дифференциации?» (PDF) . Истории оптимизации, Documenta Matematica . Дополнительный том ISMP: 389–400. дои : 10.4171/dms/6/38 . ISBN 978-3-936609-58-5 .

[lin1976-5] Линнаинмаа, Сеппо (1976). «Разложение Тейлора накопленной ошибки округления». БИТ Численная математика . 16 (2): 146–160. дои : 10.1007/BF01931367 . S2CID 122357351 .

[demm22-6] Максимилиан Э. Шюле, Максимилиан Шпрингер, Альфонс Кемпер , Томас Нойманн (2022). «Оптимизация кода LLVM для автоматического дифференцирования». Материалы шестого семинара по управлению данными для сквозного машинного обучения . стр. 1–4. дои : 10.1145/3533028.3533302 . ISBN 9781450393751 . S2CID 248853034 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[7] Бартоломью-Биггс, Майкл; Браун, Стивен; Кристиансон, Брюс; Диксон, Лоуренс (2000). «Автоматическое дифференцирование алгоритмов». Журнал вычислительной и прикладной математики . 124 (1–2): 171–190. Бибкод : 2000JCoAM.124..171B . дои : 10.1016/S0377-0427(00)00422-2 . hdl : 2299/3010 .

[ssdbm21-9] Максимилиан Э. Шюле, Харальд Ланг, Максимилиан Шпрингер, Альфонс Кемпер , Томас Нойманн , Стефан Гюннеманн (2021). «Машинное обучение в базе данных с использованием SQL на графических процессорах». 33-я Международная конференция по управлению научными и статистическими базами данных . стр. 25–36. дои : 10.1145/3468791.3468840 . ISBN 9781450384131 . S2CID 235386969 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[dpd-10] Максимилиан Э. Шюле, Харальд Ланг, Максимилиан Шпрингер, Альфонс Кемпер , Томас Нойманн , Стефан Гюннеманн (2022). «Рекурсивный SQL и поддержка графических процессоров для машинного обучения в базе данных» . Распределенные и параллельные базы данных . 40 (2–3): 205–259. дои : 10.1007/s10619-022-07417-7 . S2CID 250412395 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[11] Науманн, Уве (апрель 2008 г.). «Оптимальное накопление якобиана NP-полное». Математическое программирование . 112 (2): 427–441. CiteSeerX 10.1.1.320.5665 . дои : 10.1007/s10107-006-0042-z . S2CID 30219572 .

[12] «Библиотека прототипов AADC» . 22 июня 2022 г. – через GitHub.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[а]

[8]

[9]

[10]

[11]