ПробОнто

ПробОнто
Ключевые слова	Статистика , Распределение вероятностей
Цель	Проектируйте, внедряйте и поддерживайте базу знаний и онтологию вероятностных распределений.
Продолжительность	2015 –
Веб-сайт	пробонто .org

ProbOnto — база знаний и онтология вероятностных распределений . ProbOnto 2.5 (выпущен 16 января 2017 г.) содержит более 150 одно- и многомерных распределений и альтернативных параметризаций, более 220 связей и формул повторной параметризации, поддерживая также кодирование эмпирических и одномерных смешанных распределений .

Введение

Изначально ProbOnto был разработан для облегчения кодирования моделей нелинейных смешанных эффектов и их аннотаций на языке разметки фармакометрики (PharmML). разработан ДДМоРе, проект «Инициатива по инновационным лекарственным средствам» . Однако ProbOnto благодаря своей общей структуре может применяться на других платформах и инструментах моделирования для кодирования и аннотирования различных моделей, применимых к дискретным (например, счетным , категориальным и времени до события ) и непрерывным данным.

База знаний

Обзор поддерживаемых распределений в ProbOnto версии 2.5 и взаимосвязи между одномерными распределениями вероятностей.

В базе знаний для каждого дистрибутива хранятся:

• Плотность вероятности или массы функции и, где возможно, кумулятивное распределение , опасности и выживания . функции
• Связанные величины, такие как среднее значение, медиана, мода и дисперсия.
• Определения параметров и поддержки /диапазона, а также тип распределения.
• LaTeX и R для математических функций. Код
• Определение модели и ссылки.

Отношения

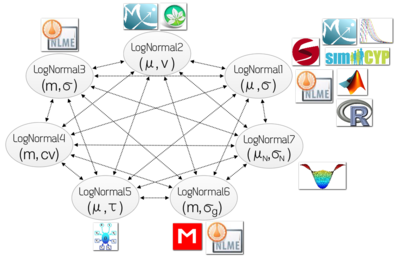
ProbOnto хранит в версии 2.5 более 220 связей между одномерными распределениями с повторной параметризацией в качестве особого случая, см. рисунок. Хотя в литературе этой формой отношений часто пренебрегают, и авторы концентрируют одну конкретную форму для каждого дистрибутива, они имеют решающее значение с точки зрения совместимости. ProbOnto фокусируется на этом аспекте и предлагает более 15 дистрибутивов с альтернативными параметризациями.

Альтернативные параметризации

Многие распределения определяются математически эквивалентными, но алгебраически разными формулами. Это приводит к проблемам при обмене моделями между программными инструментами. Следующие примеры иллюстрируют это.

Нормальное распределение

Нормальное распределение можно определить как минимум тремя способами.

• Normal1(μ,σ) со средним значением µ и стандартным отклонением σ

$P(x;{\boldsymbol {\mu }},{\boldsymbol {\sigma }})={\frac {1}{\sigma {\sqrt {2\pi }}}}\exp {\Big [}-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}{\Big ]}$

• Normal2(μ,y) со средним значением μ и дисперсией y = σ^2 или

$P(x;{\boldsymbol {\mu }},{\boldsymbol {v}})={\frac {1}{{\sqrt {v}}{\sqrt {2\pi }}}}\exp {\Big [}-{\frac {(x-\mu )^{2}}{2v}}{\Big ]}$

• Normal3(μ,τ) со средним значением μ и точностью τ = 1/y = 1/σ^2.

$P(x;{\boldsymbol {\mu }},{\boldsymbol {\tau }})={\sqrt {\frac {\tau }{2\pi }}}\exp {\Big [}-{\frac {\tau }{2}}(x-\mu )^{2}{\Big ]}$

Формулы повторной параметризации

Следующие формулы можно использовать для перерасчета трех различных форм нормального распределения (мы используем сокращения, т.е. $N1$ вместо $Normal1$ и т. д.)

• $N1(\mu ,\sigma )\rightarrow N2(\mu ,v):v=\sigma ^{2}{\mbox{ and }}N2(\mu ,v)\rightarrow N1(\mu ,\sigma ):\sigma ={\sqrt {v}};$

• $N1(\mu ,\sigma )\rightarrow N3(\mu ,\tau ):\tau =1/\sigma ^{2}{\mbox{ and }}N3(\mu ,\tau )\rightarrow N1(\mu ,\sigma ):\sigma =1/{\sqrt {\tau }};$

• $N2(\mu ,v)\rightarrow N3(\mu ,\tau ):\tau =1/v{\mbox{ and }}N3(\mu ,\tau )\rightarrow N2(\mu ,v):v=1/\tau .$

Логнормальное распределение

В случае логнормального распределения вариантов больше. Это связано с тем, что его можно параметризовать параметрами в натуральном и логарифмическом масштабе, см. рисунок.

Обзор параметризации логнормальных распределений.

Поддержка различных параметризаций логарифмически нормального распределения в различных инструментах и ​​их соединениях, примеры см. в тексте. Визуализированные инструменты: Matlab (поддерживает LN1), MCSim (LN6), Monolix (LN2 и LN3), PFIM (LN2 и LN3), Phoenix NLME (LN1, LN3 и LN6), PopED (LN7), R (язык программирования) (LN1). ), Simcyp Simulator (LN1), Simulx (LN1) и winBUGS (LN5)

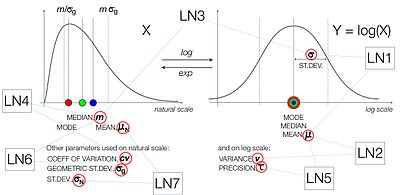
Доступные формы в ProbOnto 2.0:

• LogNormal1(μ,σ) со средним значением μ и стандартным отклонением σ, оба в логарифмической шкале.

$P(x;{\boldsymbol {\mu }},{\boldsymbol {\sigma }})={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp {\Big [}{\frac {-(\log x-\mu )^{2}}{2\sigma ^{2}}}{\Big ]}$

• LogNormal2(μ,y) со средним значением μ и дисперсией y, оба в логарифмическом масштабе.

$P(x;{\boldsymbol {\mu }},{\boldsymbol {v}})={\frac {1}{x{\sqrt {v}}{\sqrt {2\pi }}}}\exp {\Big [}{\frac {-(\log x-\mu )^{2}}{2v}}{\Big ]}$

• LogNormal3(m,σ) с медианой m в естественном масштабе и стандартным отклонением σ в логарифмическом масштабе.

$P(x;{\boldsymbol {m}},{\boldsymbol {\sigma }})={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp {\Big [}{\frac {-[\log(x/m)]^{2}}{2\sigma ^{2}}}{\Big ]}$

• LogNormal4(m,cv) с медианой m и коэффициентом вариации cv, оба в естественном масштабе.

$P(x;{\boldsymbol {m}},{\boldsymbol {cv}})={\frac {1}{x{\sqrt {\log(cv^{2}+1)}}{\sqrt {2\pi }}}}\exp {\Big [}{\frac {-[\log(x/m)]^{2}}{2\log(cv^{2}+1)}}{\Big ]}$

• LogNormal5(μ,τ) со средним значением μ и точностью τ, оба в логарифмическом масштабе.

$P(x;{\boldsymbol {\mu }},{\boldsymbol {\tau }})={\sqrt {\frac {\tau }{2\pi }}}{\frac {1}{x}}\exp {\Big [}{-{\frac {\tau }{2}}(\log x-\mu )^{2}}{\Big ]}$

• LogNormal6(m,σg ₎ с медианой m и геометрическим стандартным отклонением σg _, оба в естественном масштабе.

$P(x;{\boldsymbol {m}},{\boldsymbol {\sigma _{g}}})={\frac {1}{x\log(\sigma _{g}){\sqrt {2\pi }}}}\exp {\Big [}{\frac {-[\log(x/m)]^{2}}{2\log ^{2}(\sigma _{g})}}{\Big ]}$

• LogNormal7(μ _N ,σ _N ) со средним значением μ _N и стандартным отклонением σ _N в естественной шкале.

$P(x;{\boldsymbol {\mu _{N}}},{\boldsymbol {\sigma _{N}}})={\frac {1}{x{\sqrt {2\pi \log {\Big (}1+\sigma _{N}^{2}/\mu _{N}^{2}{\Big )}}}}}\exp {\Bigg (}{\frac {-{\Big [}\log(x)-\log {\Big (}{\frac {\mu _{N}}{\sqrt {1+\sigma _{N}^{2}/\mu _{N}^{2}}}}{\Big )}{\Big ]}^{2}}{2\log {\Big (}1+\sigma _{N}^{2}/\mu _{N}^{2}{\Big )}}}{\Bigg )}$

В базе знаний ProbOnto хранятся такие формулы повторной параметризации, чтобы обеспечить правильный перевод моделей между инструментами.

Примеры повторной параметризации

Рассмотрим ситуацию, когда хотелось бы запустить модель с использованием двух разных оптимальных инструментов проектирования, например PFIM. и ПопЭД. Первый поддерживает параметризацию LN2, второй LN7 соответственно. Поэтому требуется повторная параметризация, иначе два инструмента дадут разные результаты.

Для перехода $LN2(\mu ,v)\rightarrow LN7(\mu _{N},\sigma _{N})$ следующие формулы имеют место $\mu _{N}=\exp(\mu +v/2){\text{ and }}\sigma _{N}=\exp(\mu +v/2){\sqrt {\exp(v)-1}}$.

Для перехода $LN7(\mu _{N},\sigma _{N})\rightarrow LN2(\mu ,v)$ следующие формулы имеют место $\mu =\log {\Big (}\mu _{N}/{\sqrt {1+\sigma _{N}^{2}/\mu _{N}^{2}}}{\Big )}{\text{ and }}v=\log(1+\sigma _{N}^{2}/\mu _{N}^{2})$.

Все остальные формулы перепараметризации можно найти в спецификации на сайте проекта.

Онтология

База знаний строится на основе простой онтологической модели. По своей сути распределение вероятностей представляет собой экземпляр своего класса, специализацию класса математических объектов. Распределение относится к ряду других индивидуумов, которые являются экземплярами различных категорий в онтологии. Например, это параметры и связанные с ними функции, связанные с заданным распределением вероятностей. Эта стратегия обеспечивает богатое представление атрибутов и связей между объектами предметной области. Онтологию можно рассматривать как концептуальную схему в области математики, и она реализована как база знаний PowerLoom. Версия OWL создается программно с использованием Jena API.

Результаты ProbOnto предоставляются в качестве дополнительных материалов и публикуются на веб-сайте probonto.org или ссылаются на него. Версия ProbOnto для OWL доступна через службу поиска онтологии (OLS). для облегчения простого поиска и визуализации контента. Кроме того, API OLS предоставляет методы для программного доступа к ProbOnto и его интеграции в приложения. ProbOnto также зарегистрирован на портале BioSharing.

ПробОнто в PharmML

Интерфейс PharmML предоставляется в виде общей схемы XML для определения распределений и их параметров. Доступ к определяющим функциям, таким как функция плотности вероятности (PDF), функция массы вероятности (PMF), функция риска (HF) и функция выживания (SF), можно получить с помощью методов, предусмотренных в схеме PharmML.

Используйте пример

В этом примере показано, как распределение Пуассона с нулевым расширением кодируется с использованием его кодового имени и объявления его параметров («rate» и «probabilityOfZero»). Параметрам модели Lambda и P0 присвоены кодовые имена параметров.

<Distribution>
    <po:ProbOnto name="ZeroInflatedPoisson1">
        <po:Parameter name="rate">
            <ct:Assign>
                <ct:SymbRef symbIdRef="Lambda" />
            </ct:Assign>
        </po:Parameter>
        <po:Parameter name="probabilityOfZero">
            <ct:Assign>
                <ct:SymbRef symbIdRef="P0" />
            </ct:Assign>
        </po:Parameter>
    </po:ProbOnto>
</Distribution>

Чтобы однозначно указать любой данный дистрибутив с помощью ProbOnto, достаточно объявить его кодовое имя и кодовые имена его параметров. Больше примеров и подробную спецификацию можно найти на сайте проекта.

См. также

• Список вероятностных распределений
• Онтология (информатика)
• Отношения между распределениями вероятностей
• Язык веб-онтологии

Внешние ссылки

• Официальный сайт
• Диаграмма Лимиса
• Ultimate Univariate Probability Distribution Explorer – скорее всего, самая большая бесплатная коллекция одномерных распределений и их функций.
• UncertML