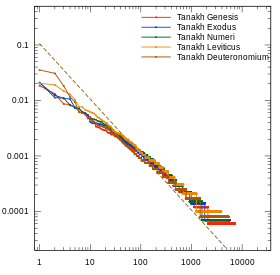Закон Ципфа

О лингвистическом законе о длине слова см. Закон сокращения Ципфа .

Закон Ципфа о войне и мире . Нижний график показывает остаток от разделения закона Ципфа. Это показывает, что сохраняется значительная закономерность, не подпадающая под закон Ципфа.

График частоты каждого слова в зависимости от его частотного ранга для двух англоязычных текстов: « Калпепера Полные травы» (1652 г.) и Герберта Уэллса » «Война миров (1898 г.) в логарифмической шкале. Пунктирная линия — идеальный закон y ∝ 1/ x .

Закон Ципфа ( / z ɪ f / , Немецкий: [t͡sɪpf] ) — это эмпирический закон , который часто приблизительно соблюдается, когда список измеренных значений отсортирован в порядке убывания. что значение n- й записи обратно пропорционально n Он утверждает , .

Самый известный пример закона Ципфа применим к таблице частот слов в тексте или корпусе естественного языка : $${\text{word frequency}}\propto {\frac {1}{\text{word rank}}}.$$ Обычно обнаруживается, что самое употребительное слово встречается примерно в два раза чаще, чем следующее по употреблению, в три раза чаще, чем третье по употреблению, и так далее. Например, в коричневом корпусе американского английского текста слово « the » является наиболее часто встречающимся словом и само по себе составляет почти 7% всех появлений слов (69 971 из чуть более 1 миллиона). В соответствии с законом Ципфа, слово « of » на втором месте составляет чуть более 3,5% слов (36 411 вхождений), за ним следуют « и » (28 852). Его часто используют в следующей форме, называемой законом Ципфа-Мандельброта : $${\text{frequency}}\propto {\frac {1}{({\text{rank}}+b)^{a}}}$$где $a,b$ являются подогнанными параметрами, при этом $a\approx 1$, и $b\approx 2.7$.

Этот закон назван в честь американского лингвиста Джорджа Кингсли Зипфа . и до сих пор является важным понятием в количественной лингвистике . Было обнаружено, что это применимо ко многим другим типам данных, изучаемых в физических и социальных науках.

В математической статистике эта концепция была формализована как распределение Ципфа : семейство связанных дискретных распределений вероятностей, чье частотно-ранговое распределение является соотношением обратного степенного закона . Они связаны с законом Бенфорда и распределением Парето .

Некоторые наборы эмпирических данных, зависящих от времени, несколько отклоняются от закона Ципфа. Такие эмпирические распределения называются квазизипфовыми .

История

В 1913 году немецкий физик Феликс Ауэрбах заметил обратную пропорциональность между численностью населения городов и их рангами при сортировке по убыванию этой переменной.

Закон Ципфа был открыт раньше Ципфа. французского стенографиста Жана-Батиста Эступа » « Gammes Stenographiques (4-е изд.) в 1916 г., с Дж. Дьюи в 1923 г., и с Э. Кондоном в 1928 г.

Такое же соотношение частот слов в текстах на естественном языке наблюдал Джордж Ципф в 1932 году. но он никогда не утверждал, что создал его. На самом деле Ципф не любил математику. В своей публикации 1932 г. автор с пренебрежением отзывается о причастности математики к языкознанию, там же, с. 21: (…) позвольте мне сказать здесь ради любого математика, который может планировать более точно сформулировать последующие данные, способность высокоинтенсивного положительного стать высокоинтенсивным отрицательным, по моему мнению, привносит дьявола в формулу в виде ${\sqrt {-i}}$. Единственное математическое выражение, которое использовал Зипф, выглядит . как б ² = константа, которую он «позаимствовал» из публикации Альфреда Дж. Лотки 1926 года.

Было обнаружено, что такая же взаимосвязь наблюдается во многих других контекстах и ​​для других переменных, помимо частоты. Например, когда корпорации ранжируются по убыванию размера, оказывается, что их размеры обратно пропорциональны рангу. Такое же соотношение наблюдается и для личных доходов (где оно называется принципом Парето). ), количество людей, смотрящих один и тот же телеканал, ноты в музыке, клеток транскриптомы , и многое другое.

В 1992 году биоинформатик Вэньтянь Ли опубликовал небольшую статью. показывая, что закон Ципфа проявляется даже в случайно сгенерированных текстах. Он включал доказательство того, что степенная форма закона Ципфа была побочным продуктом упорядочивания слов по рангу.

Формальное определение

Закон Ципфа

Функция массы вероятности PMF Zipf для N = 10 в логарифмическом масштабе. Горизонтальная ось — индекс k . (Функция определена только при целочисленных значениях k . Соединительные линии не указывают на непрерывность.)
Кумулятивная функция распределения Zipf CDF для N = 10. Горизонтальная ось — индекс k . (Функция определена только при целочисленных значениях k . Соединительные линии не указывают на непрерывность.)
Параметры	$s\geq 0\,$ ( настоящий ) $N\in \{1,2,3\ldots \}$ ( целое число )
Поддерживать	$k\in \{1,2,\ldots ,N\}$
ПМФ	${\frac {1/k^{s}}{H_{N,s}}}$ где H N,s — номер N -й обобщенной гармоники.
CDF	${\frac {H_{k,s}}{H_{N,s}}}$
Иметь в виду	${\frac {H_{N,s-1}}{H_{N,s}}}$
Режим	$1\,$
Дисперсия	${\frac {H_{N,s-2}}{H_{N,s}}}-{\frac {H_{N,s-1}^{2}}{H_{N,s}^{2}}}$
Энтропия	${\frac {s}{H_{N,s}}}\sum \limits _{k=1}^{N}{\frac {\ln(k)}{k^{s}}}+\ln(H_{N,s})$
МГФ	${\frac {1}{H_{N,s}}}\sum \limits _{n=1}^{N}{\frac {e^{nt}}{n^{s}}}$
CF	${\frac {1}{H_{N,s}}}\sum \limits _{n=1}^{N}{\frac {e^{int}}{n^{s}}}$

Формально распределение Ципфа на N элементах сопоставляет элементу ранга k (считая с 1) вероятность

$f(k;N)={\frac {1}{H_{N}}}\,{\frac {1}{k}}$

где H _N — нормировочная константа, N- й номер гармоники :

$H_{N}=\sum _{k=1}^{N}{\frac {1}{k}}\ .$

Распределение иногда обобщают до обратно-степенного закона с показателем степени s вместо 1. А именно,

$f(k;N,s)={\frac {1}{H_{N,s}}}\,{\frac {1}{k^{s}}}$

где H _{N , s} — номер обобщенной гармоники

$H_{N,s}=\sum _{k=1}^{N}{\frac {1}{k^{s}}}\ .$

Обобщенное распределение Ципфа можно расширить до бесконечного числа элементов ( N = ∞), только если показатель степени s превышает 1. В этом случае константа нормализации H _{N , s} становится дзета-функцией Римана ,

$\zeta (s)=\sum _{k=1}^{\infty }{\frac {1}{k^{s}}}<\infty \ .$

Если показатель степени s равен 1 или меньше, константа нормализации H _{N , s} расходится, когда N стремится к бесконечности.

Эмпирическое тестирование

Эмпирически набор данных можно проверить, чтобы увидеть, применим ли закон Ципфа, проверив степень соответствия эмпирического распределения гипотетическому степенному закону распределения с помощью теста Колмогорова-Смирнова , а затем сравнив (логарифмическое) отношение правдоподобия степенного закона. распределение на альтернативные распределения, такие как экспоненциальное распределение или логнормальное распределение.

Закон Ципфа можно визуализировать, нанеся данные о частоте элементов на логарифмический график, где оси представляют собой логарифм рангового порядка и логарифм частоты. Данные соответствуют закону Ципфа с показателем степени s в той степени, в которой график аппроксимирует линейную (точнее, аффинную ) функцию с наклоном - s . Для показателя степени s = 1 можно также построить график обратной зависимости частоты (среднего межсловного интервала) от ранга или обратной величины ранга от частоты и сравнить результат с линией, проходящей через начало координат, с наклоном 1.

Статистические объяснения

Хотя закон Ципфа справедлив для большинства естественных языков и даже для некоторых неестественных, таких как эсперанто. и Токи Пона , причина до сих пор не совсем понятна. Недавние обзоры генеративных процессов для закона Ципфа включают Митценмахера , «Краткую историю генеративных моделей для степенного закона и логнормального распределения», и Симкин, «Изобретая заново Уиллис».

Однако частично это можно объяснить статистическим анализом случайно сгенерированных текстов. Вэньтянь Ли показал, что в документе, в котором каждый символ выбирается случайным образом из равномерного распределения всех букв (плюс пробел), «слова» разной длины следуют макротенденции закона Ципфа (более вероятные слова являются самыми короткими и имеют одинаковую вероятность). В 1959 году Витольд Белевич с хорошим поведением заметил, что если какое-либо из большого класса статистических распределений (не только нормальное распределение ) выражается через ранги и разлагается в ряд Тейлора , то усечение этого ряда в первом порядке приводит к формуле Ципфа. закон. Далее, усечение ряда Тейлора во втором порядке привело к закону Мандельброта .

Другим возможным объяснением является принцип наименьших усилий :Сам Ципф предположил, что ни говорящие, ни слушающие, использующие данный язык, не хотят работать больше, чем необходимо, чтобы достичь понимания, и процесс, который приводит к примерно равному распределению усилий, приводит к наблюдаемому распределению Ципфа.

Минимальное объяснение предполагает, что слова генерируются обезьянами, печатающими случайным образом . Если язык генерируется случайным набором текста одной обезьяной с фиксированной и ненулевой вероятностью нажатия каждой буквенной клавиши или пробела, то слова (строки букв, разделенные пробелами), создаваемые обезьяной, подчиняются закону Ципфа.

Другой возможной причиной распределения Ципфа является процесс предпочтительной привязанности , при котором ценность x предмета имеет тенденцию расти со скоростью, пропорциональной x (интуитивно, « богатые становятся богаче » или «успех порождает успех»). Такой процесс роста приводит к распределению Юла-Саймона , которое, как было показано, соответствует частоте слов в зависимости от ранга в языке. и население в зависимости от ранга города лучше, чем закон Ципфа. Первоначально он был выведен Юлом для объяснения численности населения в зависимости от ранга вида, а Саймоном применён к городам.

Подобное объяснение основано на моделях атласов — системах сменных положительнозначных диффузионных процессов с параметрами дрейфа и дисперсии, зависящими только от ранга процесса. Математически было показано, что закон Ципфа справедлив для моделей Атласа, удовлетворяющих определенным естественным условиям регулярности.

Связанные законы

Обобщением закона Ципфа является закон Ципфа-Мандельброта , предложенный Бенуа Мандельбротом , частоты которого составляют:

$f(k;N,q,s)={\frac {1}{C}}\,{\frac {1}{(k+q)^{s}}}.\,$

Константа C представляет собой дзета-функцию Гурвица, оцениваемую в s .

Распределения Зипфа можно получить из распределений Парето путем замены переменных.

Распределение Ципфа иногда называют дискретным распределением Парето. потому что оно аналогично непрерывному распределению Парето точно так же, как дискретное равномерное распределение аналогично непрерывному равномерному распределению .

Хвостовые частоты распределения Юла – Саймона примерно равны

$f(k;\rho )\approx {\frac {[{\text{constant}}]}{k^{\rho +1}}}$

для любого выбора ρ > 0.

В параболическом фрактальном распределении логарифм частоты представляет собой квадратичный многочлен от логарифма ранга. Это может заметно улучшить соответствие по сравнению с простым степенным соотношением. Как и фрактальная размерность, можно рассчитать размерность Ципфа, которая является полезным параметром при анализе текстов.

Утверждалось, что закон Бенфорда представляет собой частный ограниченный случай закона Ципфа. причем связь между этими двумя законами объясняется тем, что оба они происходят из масштабно-инвариантных функциональных соотношений статистической физики и критических явлений. Отношения вероятностей в законе Бенфорда не постоянны. Старшие цифры данных, удовлетворяющих закону Ципфа с s = 1, удовлетворяют закону Бенфорда.

$n$	Закон Бенфорда: $P(n)=$ $\log _{10}(n+1)-\log _{10}(n)$	${\frac {\log(P(n)/P(n-1))}{\log(n/(n-1))}}$
1	0.30103000
2	0.17609126	−0.7735840
3	0.12493874	−0.8463832
4	0.09691001	−0.8830605
5	0.07918125	−0.9054412
6	0.06694679	−0.9205788
7	0.05799195	−0.9315169
8	0.05115252	−0.9397966
9	0.04575749	−0.9462848

События

Размеры города

После наблюдения Ауэрбаха 1913 года было проведено тщательное исследование закона Ципфа для размеров городов. Однако более поздние эмпирические и теоретический исследования поставили под сомнение актуальность закона Ципфа для городов.

Частоты слов в естественных языках

График закона Ципфа для первых 10 миллионов слов в 30 Arc.Ask3.Ruх (по состоянию на октябрь 2015 г.) в логарифмическом масштабе.

Во многих текстах на человеческих языках частота слов примерно соответствует распределению Ципфа с показателем степени , близким к 1: то есть наиболее распространенное слово встречается примерно в n раз чаще, чем n -е наиболее распространенное.

Фактический график ранг-частота текста на естественном языке в некоторой степени отклоняется от идеального распределения Ципфа, особенно на двух концах диапазона. Отклонения могут зависеть от языка, темы текста, автора, от того, был ли текст переведен с другого языка, от используемых правил правописания. Некоторые отклонения неизбежны из-за ошибки выборки .

На низкочастотном конце, где ранг приближается к N , график принимает форму лестницы, поскольку каждое слово может встречаться только целое число раз.

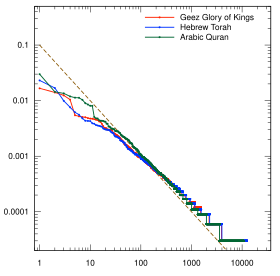
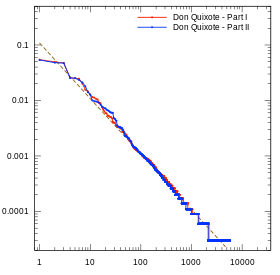
• Графики закона Ципфа для нескольких языков
• 
  Тексты на немецком (1669 г.), русском (1972 г.), французском (1865 г.), итальянском (1840 г.) и средневековом английском (1460 г.)
• 
  Сервантеса « Дон Кихот, часть I» ( испанский , 1605 г.) и Ассиса « Дом Касмурро» ( португальский , 1899 г.)
• 
  Геэз (14 век), арабский (~ 650), иврит (500–800), все с гласными.
• 
  Лхасский тибетский , китайский , вьетнамский , все с отдельными слогами.
• 
  Библейские тексты: Пятикнижие из латинской Вульгаты и русская Синодальная Библия , четыре Евангелия из византийского греческого большинства. версии
• 
  Дон Кихот Сервантеса, часть I (1605 г.) и часть II (1615 г.)
• 
  Первые пять книг Ветхого Завета ( Торы ) на иврите, с гласными.
• 
  Первые пять книг Ветхого Завета ( Пятикнижия ) в латинской Вульгаты . версии
• 
  Первые четыре книги Нового Завета ( Евангелия ) в латинской Вульгаты . версии

Логарифмический график частоты слов в Википедии (27 ноября 2006 г.). «Самыми популярными словами являются «the», «of» и «and», как и ожидалось. Закон Ципфа соответствует средней линейной части кривой, примерно следующей зеленой (1/ x ) линии, тогда как ранняя часть ближе к пурпурной (1/ x ^0.5 ) линия, а последняя часть ближе к голубому (1/( k + x ) ^2.0 ) линия. Эти линии соответствуют трем различным параметризациям распределения Ципфа – Мандельброта, в целом нарушенному степенному закону с тремя сегментами: головой, серединой и хвостом.

В некоторых романских языках частоты примерно дюжины наиболее частых слов значительно отклоняются от идеального распределения Ципфа, поскольку эти слова включают артикли, склоняемые по грамматическому роду и числу .

Во многих восточноазиатских языках, таких как китайский , лхасский тибетский и вьетнамский , каждое «слово» состоит из одного слога ; это английское слово часто переводится как соединение двух таких слогов. Таблица частотности рангов для этих «слов» значительно отклоняется от идеального закона Ципфа на обоих концах диапазона.

Даже в английском языке отклонения от идеального закона Ципфа становятся более очевидными при изучении больших коллекций текстов. Анализ корпуса из 30 000 английских текстов показал, что только около 15% текстов в нем хорошо соответствуют закону Ципфа. Небольшие изменения в определении закона Ципфа могут увеличить этот процент почти до 50%.

В этих случаях наблюдаемое частотно-ранговое соотношение можно более точно смоделировать с помощью отдельных распределений законов Ципфа – Мандельброта для разных подмножеств или подтипов слов. Так обстоит дело с частотно-ранговым графиком первых 10 миллионов слов английской Википедии. В частности, частоты закрытого класса служебных слов в английском языке лучше описываются значениями s ниже 1, в то время как рост словарного запаса открытого типа с увеличением размера документа и размера корпуса требует s больше 1 для сходимости Обобщенного гармонического ряда .

Уэллса «Война миров» в открытом тексте, в книжном коде и в шифре Виженера.

Когда текст шифруется таким образом, что каждое появление каждого отдельного слова открытого текста всегда отображается в одно и то же зашифрованное слово (как в случае шифров простой замены , таких как шифры Цезаря , или простых шифров кодовой книги ), частотный ранг распространение не затронуто. С другой стороны, если отдельные вхождения одного и того же слова могут быть сопоставлены с двумя или более разными словами (как это происходит с шифром Виженера ), распределение Ципфа обычно будет иметь плоскую часть на высокочастотном конце.

Приложения

Закон Ципфа использовался для извлечения параллельных фрагментов текстов из сопоставимых корпусов. Лоранс Дойл и другие предложили применить закон Ципфа для обнаружения инопланетного языка в поисках внеземного разума .

Частотно-ранговое распределение слов часто свойственно автору и мало меняется с течением времени. Эта особенность была использована при анализе текстов на предмет установления авторства.

группы словоподобных знаков в рукописи Войнича XV века удовлетворяют закону Ципфа, предполагая, что текст, скорее всего, не является мистификацией, а скорее написан на непонятном языке или зашифрован. Было обнаружено, что

См. также

• Правило 1% (Интернет-культура) – гипотеза о том, что в виртуальном сообществе будет скрываться больше людей, чем будет участвовать. Страницы с краткими описаниями целей перенаправления.
• Закон Бенфорда . Наблюдение: во многих реальных наборах данных первая цифра, скорее всего, будет маленькой.
• Закон Брэдфорда - Характер ссылок в научных журналах
• Закон о краткости – Закон о лингвистике
• Демографическая гравитация
• Список частот – пустой список слов языка в корпусной лингвистике. Страницы, отображающие краткие описания целей перенаправления.
• Закон Жибрата – Экономический принцип
• Hapax legomenon - слово, которое встречается в данном тексте или записи только один раз.
• Закон Кучи - эвристика для определения отдельных слов в документе
• Эффект Кинга - явление в статистике, когда точки данных с самым высоким рейтингом являются выбросами.
• Длинный хвост - особенность некоторых статистических распределений.
• Кривая Лоренца - графическое изображение распределения дохода или богатства.
• Закон Лотки - применение закона Ципфа, описывающее частоту публикаций авторов в любой данной области.
• Закон Менцерата - Лингвистический закон
• Распределение Парето – Распределение вероятностей
• Принцип Парето - статистический принцип соотношения последствий и причин, также известный как «правило 80–20».
• Закон Прайса - физик и историк науки (1922–1983). Страницы с краткими описаниями целей перенаправления.
• Принцип наименьших усилий . Идея о том, что агенты предпочитают делать то, что проще.
• Распределение по размеру — распределение размера по рангу. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Закон эпонимии Стиглера - наблюдение, что ни одно научное открытие не названо в честь его первооткрывателя.
• Частота букв
• Самые распространенные слова в английском языке

Дальнейшее чтение

• Александр Гельбух и Григорий Сидоров (2001) «Коэффициенты законов Ципфа и кучи зависят от языка» . Учеб. CICLing -2001, Конференция по интеллектуальной обработке текста и компьютерной лингвистике , 18–24 февраля 2001 г., Мехико. Конспект лекций по информатике N 2004, ISSN   0302-9743 , ISBN   3-540-41687-0 , Springer-Verlag: 332–335.
• Кали Р. (2003) «Город как гигантский компонент: подход к закону Ципфа на основе случайных графов», Applied Economics Letters 10 : 717–720 (4)
• Шикло А. (2017); Простое объяснение загадки Ципфа с помощью нового распределения рангов, полученного из комбинаторики процесса ранжирования , доступно на SSRN: https://ssrn.com/abstract=2918642 .
• Клара Московиц , Джен Кристиансен и Ни-Ка Форд , «Клетки по количеству и размеру: чем крупнее тип клеток, тем реже они встречаются в организме – и наоборот», Scientific American , vol. 330, нет. 1 (январь 2024 г.), стр. 94–95. «Когда вы удваиваете объем клетки, частота появления клеток такого размера уменьшается вдвое», — обнаружили эколог Ян А. Хаттон из Университета Макгилла и его коллеги-исследователи закона Ципфа, говорит Хаттон. «Маленькие, безъядерные эритроциты являются, безусловно, наиболее распространенными клетками в нашем организме, тогда как сравнительно гигантские мышечные клетки в наших руках и ногах являются самыми редкими. Возможность использовать размер клетки для оценки ее частоты в организме может помочь врачам лучше понять определенные системы организма и типы клеток, которые трудно подсчитать... Исследование показывает, например, что иммунные клетки , называемые лимфоцитами, встречаются гораздо чаще, чем предполагали биологи». (стр. 94.)

Внешние ссылки

• Строгац, Стивен (29 мая 2009 г.). «Гостевая рубрика: Математика и город» . Нью-Йорк Таймс . Архивировано из оригинала 27 сентября 2015 г. Проверено 29 мая 2009 г. -Статья о законе Ципфа применительно к городскому населению.
• Видение за углом (искусственные общества подтверждают закон Ципфа)
• Статья PlanetMath о законе Ципфа
• Распределения типа «фрактальной параболики» в природе (на французском языке, с резюме на английском языке). Архивировано 24 октября 2004 г. в Wayback Machine.
• Анализ распределения доходов
• Список французских слов Zipf. Архивировано 23 июня 2007 г. в Wayback Machine.
• Список Zipf для английского, французского, испанского, итальянского, шведского, исландского, латыни, португальского и финского языков от Gutenberg Project и онлайн-калькулятор для ранжирования слов в текстах. Архивировано 8 апреля 2011 г. на Wayback Machine.
• Цитаты и закон Ципфа – Мандельброта.
• Примеры и моделирование закона Ципфа (1985)
• Сложные системы: распаковка закона Ципфа (2011)
• Закон Бенфорда, закон Ципфа и распределение Парето Теренса Тао.
• «Закон Ципфа» , Математическая энциклопедия , EMS Press , 2001 [1994]