Резонанс

Эта статья о резонансе в физике. Чтобы узнать о других значениях, см. Резонанс (значения) .

«Резонировать» перенаправляется сюда. Чтобы узнать о других значениях, см. Резонировать (значения) .

«Резонансный» перенаправляется сюда. Чтобы узнать о фонологическом термине, см. Sonorant .

Увеличение амплитуды по мере уменьшения затухания и приближения частоты к резонансной частоте ведомого затухающего простого гармонического генератора .

Резонанс возникает в колебательных динамических системах , когда внешняя изменяющаяся во времени сила совпадает с собственной частотой системы. Резонанс может возникать в различных системах, таких как механические, электрические или акустические системы, и он желателен в некоторых приложениях, таких как музыкальные инструменты или радиоприемники. Резонанс также может быть нежелательным, приводя в некоторых случаях к чрезмерным вибрациям или даже к разрушению конструкции.

Все системы, включая молекулярные системы и частицы, имеют тенденцию вибрировать с собственной частотой, зависящей от их структуры; эта частота известна как резонансная частота или резонансная частота . Когда осциллирующая сила, внешняя вибрация, применяется на резонансной частоте динамической системы, объекта или частицы, внешняя вибрация заставит систему колебаться с более высокой амплитудой (с большей силой), чем при приложении той же силы. на других, нерезонансных частотах.

Резонансные частоты системы можно определить, когда реакция на внешнюю вибрацию создает амплитуду, которая является относительным максимумом внутри системы. Небольшие периодические силы, находящиеся вблизи резонансной частоты системы, способны вызывать в системе колебания большой амплитуды за счет накопления колебательной энергии .

Резонансные явления происходят со всеми типами вибраций или волн : существует механический резонанс , орбитальный резонанс , акустический резонанс , электромагнитный резонанс, ядерный магнитный резонанс (ЯМР), электронный спиновый резонанс (ЭПР) и резонанс квантовых волновых функций . Резонансные системы можно использовать для генерации вибраций определенной частоты (например, музыкальных инструментов ) или выделения определенных частот из сложной вибрации, содержащей множество частот (например, фильтров).

Термин «резонанс» (от латинского resonantia , «эхо», от resonare , «звучать») возник из области акустики, в частности, из симпатического резонанса, наблюдаемого в музыкальных инструментах, например, когда одна струна начинает вибрировать и издавать звук после другой. поражен.

Обзор

Резонанс возникает, когда система способна хранить и легко передавать энергию между двумя или более различными режимами хранения (например, кинетическую энергию и потенциальную энергию в случае простого маятника). Однако от цикла к циклу происходят некоторые потери, называемые демпфированием . При малом затухании резонансная частота примерно равна собственной частоте системы, представляющей собой частоту невынужденных колебаний. Некоторые системы имеют несколько различных резонансных частот.

Примеры

Толкание человека на качелях — типичный пример резонанса. Нагруженные качели, маятник , имеют собственную частоту колебаний, свою резонансную частоту, и сопротивляются более быстрому или медленному толканию.

Знакомый пример — качели на детской площадке , которые действуют как маятник . Если толкнуть человека на качелях вовремя с естественным интервалом качания (его резонансной частотой), то качели будут идти все выше и выше (максимальная амплитуда), тогда как попытки толкнуть качели в более быстром или медленном темпе приводят к образованию меньших дуг. Это связано с тем, что энергия, поглощаемая качелями, максимальна, когда толчки соответствуют естественным колебаниям качелей.

Резонанс широко распространен в природе и используется во многих устройствах. Это механизм, с помощью которого практически все синусоидальные генерируются волны и вибрации. Например, при ударе по твердым предметам, таким как металл , стекло или дерево , в объекте возникают краткие резонансные вибрации. Свет и другое коротковолновое электромагнитное излучение возникает в результате резонанса на атомном уровне , например, электронов в атомах. Другие примеры резонанса включают:

• Механизмы хронометража современных часов, например балансовое колесо в механических часах и кристалл кварца в кварцевых часах.
• Приливный резонанс залива Фанди
• Акустические резонансы музыкальных инструментов человека и речевого тракта
• Разрушение хрустального бокала под воздействием музыкального тона правильной высоты (его резонансной частоты)
• Идиофоны трения , например, заставляют стеклянный предмет (стакан, бутылку, вазу) вибрировать , потирая его край кончиком пальца.
• Электрический резонанс настроенных цепей в радиоприемниках и телевизорах , позволяющих избирательно принимать радиочастоты.
• Создание когерентного света путем оптического резонанса в лазера резонаторе
• Орбитальный резонанс на примере некоторых спутников Солнечной системы . планет-гигантов и резонансных групп, таких как плутино
• Резонансы материалов в атомном масштабе лежат в основе нескольких спектроскопических методов, используемых в физике конденсированного состояния.
  • Электронный спиновый резонанс
  • Эффект Мессбауэра
  • Ядерный магнитный резонанс

Линейные системы

Резонанс проявляется во многих линейных и нелинейных системах как колебания вокруг точки равновесия. Когда система управляется синусоидальным внешним входным сигналом, измеренный выходной сигнал системы может колебаться в ответ. Отношение амплитуды установившихся колебаний на выходе к колебаниям на входе называется коэффициентом усиления, и коэффициент усиления может быть функцией частоты синусоидального внешнего входного сигнала. Пики усиления на определенных частотах соответствуют резонансам, где амплитуда колебаний измеряемого выходного сигнала непропорционально велика.

Поскольку многие линейные и нелинейные колеблющиеся системы моделируются как гармонические осцилляторы вблизи их состояния равновесия, показан вывод резонансной частоты для ведомого затухающего гармонического осциллятора. Схема RLC используется для иллюстрации связи между резонансом и передаточной функцией системы, частотной характеристикой, полюсами и нулями. На примере схемы RLC эти соединения для линейных систем более высокого порядка с несколькими входами и выходами обобщаются.

генератор

Основная статья: Гармонический генератор § Управляемые гармонические генераторы

Рассмотрим демпфированную массу на пружине, приводимую в движение синусоидальной внешней силой. Второй закон Ньютона принимает вид

$$m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}},$$

( 1 )

где m — масса, x — смещение массы от точки равновесия, F ₀ — амплитуда движения, ω — движущая угловая частота, k — жесткость пружины, с — коэффициент вязкого демпфирования. Это можно переписать в виде

$${\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\sin(\omega t),$$

( 2 )

где

• ${\textstyle \omega _{0}={\sqrt {k/m}}}$ называется незатухающей угловой частотой генератора или собственной частотой ,
• $\zeta ={\frac {c}{2{\sqrt {mk}}}}$ называется коэффициентом демпфирования .

Многие источники также называют ω ₀ резонансной частотой . Однако, как показано ниже, при анализе колебаний смещения x ( t ) резонансная частота близка, но не равна ω ₀ . В общем, резонансная частота близка к собственной частоте, но не обязательно равна ей. Пример схемы RLC в следующем разделе дает примеры различных резонансных частот для одной и той же системы.

Общее решение уравнения ( 2 ) представляет собой сумму переходного решения, которое зависит от начальных условий, и установившегося решения, которое не зависит от начальных условий и зависит только от амплитуды возбуждения F ₀ , частоты возбуждения ω , незатухающей угловой частоты ω ₀ и коэффициент демпфирования ζ . Переходное решение затухает за относительно короткий промежуток времени, поэтому для изучения резонанса достаточно рассмотреть стационарное решение.

Можно записать установившееся решение для x ( t ) как функцию, пропорциональную движущей силе с индуцированным фазы изменением φ ,

$$x(t)={\frac {F_{0}}{m{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}}\sin(\omega t+\varphi ),$$

( 3 )

где $\varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .$

Значение фазы обычно принимается в диапазоне от -180° до 0, поэтому оно представляет собой задержку фазы как для положительных, так и для отрицательных значений аргумента арктанга.

Стационарное изменение амплитуды в зависимости от относительной частоты $\omega /\omega _{0}$ и демпфирование $\zeta$ ведомого простого гармонического генератора

Резонанс возникает, когда на определенных частотах возбуждения установившаяся амплитуда x ( t ) велика по сравнению с ее амплитудой на других частотах возбуждения. Для массы на пружине резонанс физически соответствует колебаниям массы с большими смещениями от положения равновесия пружины на определенных частотах движения. Глядя на амплитуду x ( t ) как функцию частоты возбуждения ω , амплитуда максимальна на частоте возбуждения

$$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.$$

ω _r – резонансная частота этой системы. Опять же, резонансная частота не равна незатухающей угловой частоте ω ₀ генератора. Они пропорциональны, и если коэффициент демпфирования стремится к нулю, они остаются одинаковыми, но при ненулевом демпфировании они имеют разную частоту. Как показано на рисунке, резонанс может возникать и на других частотах вблизи резонансной частоты, включая ω ₀ , но максимальный отклик приходится на резонансную частоту.

Кроме того, ω _r веществен и отличен от нуля только в том случае, если ${\textstyle \zeta <1/{\sqrt {2}}}$, поэтому эта система может резонировать только тогда, когда гармонический осциллятор значительно затухает. Для систем с очень малым коэффициентом демпфирования и частотой возбуждения, близкой к резонансной частоте, установившиеся колебания могут стать очень большими.

Маятник

Для других приводных, затухающих гармонических осцилляторов, уравнения движения которых не выглядят точно так же, как масса на примере пружины, резонансная частота остается

$$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}},$$

но определения ω ₀ и ζ меняются в зависимости от физики системы. Для маятника длины ℓ и небольшого угла смещения θ уравнение ( 1 ) принимает вид

$$m\ell {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-mg\theta -c\ell {\frac {\mathrm {d} \theta }{\mathrm {d} t}}$$

и поэтому

• $\omega _{0}={\sqrt {\frac {g}{\ell }}},$
• $\zeta ={\frac {c}{2m}}{\sqrt {\frac {\ell }{g}}}.$

Схемы серии RLC

См. Также: Схема RLC § Последовательная схема.

Последовательная схема RLC

Рассмотрим цепь, состоящую из резистора с сопротивлением R , катушки индуктивности с индуктивностью L и конденсатора емкостью C, соединенных последовательно с током i ( t ) и управляемых источником напряжения с напряжением v _in ( t ). Падение напряжения в цепи равно

$L{\frac {di(t)}{dt}}+Ri(t)+V(0)+{\frac {1}{C}}\int _{0}^{t}i(\tau )d\tau =v_{\text{in}}(t).$ ( 4 )

Вместо анализа возможного решения этого уравнения, как в примере с пружиной выше, в этом разделе будет проанализирована частотная характеристика этой схемы. Принимая преобразование Лапласа уравнения ( 4 ),

$$sLI(s)+RI(s)+{\frac {1}{sC}}I(s)=V_{\text{in}}(s),$$

где I ( s ) и V _in ( s ) — преобразование Лапласа тока и входного напряжения соответственно, а s — комплексный частотный параметр в области Лапласа. Перестановка терминов,

$$I(s)={\frac {s}{s^{2}L+Rs+{\frac {1}{C}}}}V_{\text{in}}(s).$$

Напряжение на конденсаторе

Последовательная цепь RLC предоставляет несколько вариантов измерения выходного напряжения. Предположим, что интересующее выходное напряжение — это падение напряжения на конденсаторе. Как показано выше, в области Лапласа это напряжение равно

$$V_{\text{out}}(s)={\frac {1}{sC}}I(s)$$

или

$$V_{\text{out}}={\frac {1}{LC(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{\text{in}}(s).$$

Определим для этой схемы собственную частоту и коэффициент затухания:

$$\omega _{0}={\frac {1}{\sqrt {LC}}},$$

$$\zeta ={\frac {R}{2}}{\sqrt {\frac {C}{L}}}.$$

Отношение выходного напряжения к входному напряжению становится

$$H(s)\triangleq {\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}$$

H ( s ) — передаточная функция между входным напряжением и выходным напряжением. Эта передаточная функция имеет два полюса – корни многочлена в знаменателе передаточной функции – при

$$s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}}$$

( 5 )

и отсутствие нулей – корней многочлена в числителе передаточной функции. При этом при ζ ≤ 1 величина этих полюсов равна собственной частоте ω ₀ , а при ζ < 1/ ${\sqrt {2}}$, наше условие резонанса в примере с гармоническим осциллятором, полюса находятся ближе к мнимой оси, чем к реальной оси.

Оценивая H ( s ) вдоль мнимой оси s = iω , передаточная функция описывает частотную характеристику этой схемы. Аналогично, частотную характеристику можно проанализировать, приняв преобразование Фурье уравнения ( 4 ) вместо преобразования Лапласа. Передаточную функцию, которая также является сложной, можно записать как коэффициент усиления и фазу:

$$H(i\omega )=G(\omega )e^{i\Phi (\omega )}.$$

График величины Боде для напряжения на элементах последовательной цепи RLC. Собственная частота ω ₀ = 1 рад/с , коэффициент затухания ζ = 0,4 . Максимальное напряжение конденсатора ниже собственной частоты схемы, пиковое напряжение дросселя выше собственной частоты, а пиковое напряжение резистора соответствует собственной частоте с пиковым коэффициентом усиления, равным единице. Коэффициент усиления напряжения на конденсаторе и катушке индуктивности, соединенных последовательно, демонстрирует антирезонанс, при этом коэффициент усиления стремится к нулю на собственной частоте.

Синусоидальное входное напряжение на частоте ω приводит к выходному напряжению на той же частоте, которое масштабируется G ( ω ) и имеет фазовый сдвиг Φ ( ω ). Коэффициент усиления и фаза могут быть отображены в зависимости от частоты на графике Боде . Для напряжения конденсатора цепи RLC коэффициент усиления передаточной функции H ( iω ) равен

$$G(\omega )={\frac {\omega _{0}^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

( 6 )

Обратите внимание на сходство между усилением здесь и амплитудой в уравнении ( 3 ). Опять же, коэффициент усиления максимизируется на резонансной частоте.

$$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.$$

Здесь резонанс физически соответствует относительно большой амплитуде установившихся колебаний напряжения на конденсаторе по сравнению с его амплитудой на других частотах возбуждения.

Напряжение на индукторе

Резонансная частота не всегда должна принимать форму, приведенную в примерах выше. Для схемы RLC предположим, что интересующее выходное напряжение — это напряжение на катушке индуктивности. Как показано выше, в области Лапласа напряжение на катушке индуктивности равно

$$V_{\text{out}}(s)=sLI(s),$$

$$V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s),$$

$$V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}V_{\text{in}}(s),$$

используя те же определения для ω ₀ и ζ , что и в предыдущем примере. Передаточная функция между V _in ( s ) и этим новым V _out ( s ) на индукторе равна

$$H(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$$

Эта передаточная функция имеет те же полюса, что и передаточная функция в предыдущем примере, но также имеет два нуля в числителе при s = 0 . Оценивая H ( s ) вдоль мнимой оси, его коэффициент усиления становится

$$G(\omega )={\frac {\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

По сравнению с коэффициентом усиления в уравнении ( 6 ), использующим напряжение конденсатора в качестве выходного сигнала, этот коэффициент усиления равен ω. ² в числителе и, следовательно, будет иметь другую резонансную частоту, которая максимизирует усиление. Эта частота

$$\omega _{r}={\frac {\omega _{0}}{\sqrt {1-2\zeta ^{2}}}},$$

Таким образом, для той же схемы RLC, но с напряжением на катушке индуктивности в качестве выходного, резонансная частота теперь больше собственной частоты, хотя она все еще стремится к собственной частоте, поскольку коэффициент затухания стремится к нулю. То, что одна и та же схема может иметь разные резонансные частоты для разных выходных сигналов, не является противоречием. Как показано в уравнении ( 4 ), падение напряжения в цепи делится между тремя элементами схемы, и каждый элемент имеет разную динамику. Напряжение конденсатора растет медленно за счет интегрирования тока с течением времени и, следовательно, более чувствительно к более низким частотам, тогда как напряжение дросселя растет, когда ток быстро изменяется, и поэтому более чувствительно к более высоким частотам. Хотя схема в целом имеет собственную частоту, на которой она имеет тенденцию колебаться, различная динамика каждого элемента схемы заставляет каждый элемент резонировать на несколько разной частоте.

Напряжение на резисторе

Предположим, что интересующее выходное напряжение — это напряжение на резисторе. В области Лапласа напряжение на резисторе равно

$$V_{\text{out}}(s)=RI(s),$$

$$V_{\text{out}}(s)={\frac {Rs}{L\left(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}\right)}}V_{\text{in}}(s),$$

и используя ту же собственную частоту и коэффициент затухания, что и в примере с конденсатором, передаточная функция равна

$$H(s)={\frac {2\zeta \omega _{0}s}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$$

Эта передаточная функция также имеет те же полюса, что и предыдущие примеры схем RLC, но имеет только один ноль в числителе при s = 0. Для этой передаточной функции ее коэффициент усиления равен

$$G(\omega )={\frac {2\zeta \omega _{0}\omega }{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

Резонансная частота, которая максимизирует этот коэффициент усиления, равна

$$\omega _{r}=\omega _{0},$$

и коэффициент усиления равен единице на этой частоте, поэтому напряжение на резисторе резонирует на собственной частоте схемы, и на этой частоте амплитуда напряжения на резисторе равна амплитуде входного напряжения.

Антирезонанс

Основная статья: Антирезонанс

В некоторых системах наблюдается антирезонанс, который можно анализировать так же, как и резонанс. Для антирезонанса амплитуда отклика системы на определенных частотах не пропорционально мала велика, а непропорционально . В примере схемы RLC это явление можно наблюдать, анализируя одновременно катушку индуктивности и конденсатор.

Предположим, что интересующее выходное напряжение в цепи RLC представляет собой напряжение на катушке индуктивности и конденсаторе, соединенных последовательно. Уравнение ( 4 ) показало, что сумма напряжений на трех элементах схемы равна входному напряжению, поэтому измерение выходного напряжения как суммы объединенных напряжений катушки индуктивности и конденсатора равнозначно v _минус падение напряжения на резисторе. . Предыдущий пример показал, что на собственной частоте системы амплитуда падения напряжения на резисторе равна амплитуде v _in , и, следовательно, напряжение на катушке индуктивности и конденсаторе вместе взятое имеет нулевую амплитуду. Мы можем показать это с помощью передаточной функции.

Сумма напряжений катушки индуктивности и конденсатора равна

$$V_{\text{out}}(s)=(sL+{\frac {1}{sC}})I(s),$$

$$V_{\text{out}}(s)={\frac {s^{2}+{\frac {1}{LC}}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s).$$

Используя ту же собственную частоту и коэффициенты затухания, что и в предыдущих примерах, передаточная функция имеет вид

$$H(s)={\frac {s^{2}+\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$$

Этот перенос имеет те же полюса, что и предыдущие примеры, но имеет нули в точке.

$$s=\pm i\omega _{0}.$$

( 7 )

Оценивая передаточную функцию вдоль мнимой оси, ее коэффициент усиления равен

$$G(\omega )={\frac {\omega _{0}^{2}-\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$$

Вместо того, чтобы искать резонанс, т.е. пики усиления, обратите внимание, что усиление стремится к нулю при ω = ω ₀ , что дополняет наш анализ напряжения резистора. Это называется антирезонансом , который оказывает эффект, противоположный резонансу. Вместо того, чтобы приводить к непропорционально большим выходным сигналам на этой частоте, эта схема с таким выбором выходного сигнала вообще не реагирует на этой частоте. Отфильтрованная частота точно соответствует нулям передаточной функции, которые показаны в уравнении ( 7 ) и расположены на мнимой оси.

схемы серии

Эти примеры схем RLC иллюстрируют, как резонанс связан с частотной характеристикой системы. В частности, эти примеры иллюстрируют:

• Как можно найти резонансные частоты, ища пики коэффициента усиления передаточной функции между входом и выходом системы, например, на графике величины Боде
• Как резонансная частота одной системы может различаться при разных вариантах выходного сигнала системы
• Связь между собственной частотой системы, коэффициентом затухания системы и резонансной частотой системы.
• Связь между собственной частотой системы и величиной полюсов передаточной функции, указанная в уравнении ( 5 ), и, следовательно, связь между полюсами и резонансной частотой
• Связь между нулями передаточной функции и формой коэффициента усиления как функции частоты и, следовательно, связь между нулями и резонансной частотой, которая максимизирует коэффициент усиления.
• Связь между нулями передаточной функции и антирезонансом

В следующем разделе эти концепции расширяются на случай резонанса в общей линейной системе.

Обобщающий резонанс и антирезонанс для линейных систем

Далее рассмотрим произвольную линейную систему с несколькими входами и выходами. Например, в представлении в пространстве состояний третьего порядка линейная стационарная система с тремя входами и двумя выходами может быть записана как

$${\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\end{bmatrix}}=A{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+B{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},$$

$${\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}=C{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+D{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},$$

где ui ₍ ( t входные данные, xi ₍ t) — переменные состояния, y _i ) — t ) — выходные данные, а A , B , C и D — матрицы, описывающие динамику между переменными.

Эта система имеет матрицу передаточных функций , элементами которой являются передаточные функции между различными входами и выходами. Например,

$${\begin{bmatrix}Y_{1}(s)\\Y_{2}(s)\end{bmatrix}}={\begin{bmatrix}H_{11}(s)&H_{12}(s)&H_{13}(s)\\H_{21}(s)&H_{22}(s)&H_{23}(s)\end{bmatrix}}{\begin{bmatrix}U_{1}(s)\\U_{2}(s)\\U_{3}(s)\end{bmatrix}}.$$

Каждый H _ij ( s ) представляет собой скалярную передаточную функцию, связывающую один из входов с одним из выходов. Приведенные выше примеры схем RLC имели одно входное напряжение и показывали четыре возможных выходных напряжения — на конденсаторе, на катушке индуктивности, на резисторе и на конденсаторе и катушке индуктивности, соединенных последовательно, — каждое со своей собственной передаточной функцией. Если бы схема RLC была настроена для измерения всех четырех выходных напряжений, эта система имела бы матрицу передаточной функции 4×1, связывающую один вход с каждым из четырех выходов.

Оцениваемое вдоль мнимой оси, каждое H _ij ( iω ) можно записать как коэффициент усиления и фазовый сдвиг:

$$H_{ij}(i\omega )=G_{ij}(\omega )e^{i\Phi _{ij}(\omega )}.$$

Пики усиления на определенных частотах соответствуют резонансам между входом и выходом этой передаточной функции, при условии, что система стабильна .

Каждую передаточную функцию H _ij ( s ) также можно записать как дробь, числитель и знаменатель которой являются полиномами от s .

$$H_{ij}(s)={\frac {N_{ij}(s)}{D_{ij}(s)}}.$$

Комплексные корни числителя называются нулями, а комплексные корни знаменателя — полюсами. Для стабильной системы положения этих полюсов и нулей на комплексной плоскости дают некоторое представление о том, может ли система резонировать или антирезонансировать и на каких частотах. В частности, любую стабильную или минимально стабильную комплексно-сопряженную пару полюсов с мнимыми компонентами можно записать через собственную частоту и коэффициент затухания как

$$s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}},$$

как в уравнении ( 5 ). Собственная частота ω ₀ этого полюса представляет собой величину положения полюса на комплексной плоскости, а коэффициент затухания этого полюса определяет, насколько быстро затухают колебания. В общем,

• Комплексно-сопряженные пары полюсов вблизи мнимой оси соответствуют пику или резонансу частотной характеристики вблизи собственной частоты полюса. Если пара полюсов находится на воображаемой оси, коэффициент усиления на этой частоте бесконечен.
• Комплексно-сопряженные пары нулей вблизи мнимой оси соответствуют провалу или антирезонансу в частотной характеристике вблизи частоты нуля, т. е. частоты, равной величине нуля. Если пара нулей находится на мнимой оси, усиление равно нулю на этой частоте.

В примере схемы RLC первое обобщение, касающееся полюсов и резонанса, наблюдается в уравнении ( 5 ). Второе обобщение, связывающее нули с антирезонансом, наблюдается в уравнении ( 7 ). В примерах гармонического генератора, напряжения конденсатора цепи RLC и напряжения катушки индуктивности цепи RLC «полюса вблизи мнимой оси» соответствуют значительному затуханию ζ < 1/. ${\sqrt {2}}$.

Стоячие волны

Основная статья: Стоячая волна

Масса на пружине имеет одну собственную частоту , так как имеет одну степень свободы.

Физическая система может иметь столько собственных частот, сколько у нее степеней свободы , и может резонировать вблизи каждой из этих собственных частот. Масса на пружине, имеющая одну степень свободы, имеет одну собственную частоту. Двойной маятник , имеющий две степени свободы, может иметь две собственные частоты. По мере увеличения числа связанных гармонических осцилляторов время, необходимое для передачи энергии от одного к другому, становится значительным. Системы с очень большим числом степеней свободы можно рассматривать как непрерывные , а не как имеющие дискретные осцилляторы.

Энергия передается от одного генератора к другому в виде волн. Например, струну гитары или поверхность воды в чаше можно смоделировать как континуум небольших связанных осцилляторов, по которым могут распространяться волны. Во многих случаях эти системы могут резонировать на определенных частотах, образуя стоячие волны с колебаниями большой амплитуды в фиксированных положениях. Резонанс в виде стоячих волн лежит в основе многих известных явлений, таких как звук музыкальных инструментов, электромагнитные полости, используемые в лазерах и микроволновых печах, а также энергетические уровни атомов.

Стоячие волны на верёвке

( Стоячая волна черным цветом), возникающая, когда две волны, движущиеся слева и справа, встречаются и накладываются друг на друга.

Когда струна фиксированной длины приводится в движение с определенной частотой, волна распространяется вдоль струны с той же частотой. Волны отражаются от концов струны, и в конечном итоге устойчивое состояние достигается , когда волны распространяются в обоих направлениях. Форма волны представляет собой суперпозицию волн.

На определенных частотах кажется, что установившийся сигнал не распространяется по струне. В фиксированных положениях, называемых узлами , строка никогда не смещается . Между узлами струна колеблется и ровно на полпути между узлами – в положениях, называемых антиузлами – колебания имеют наибольшую амплитуду.

Стоячие волны в струне – основная мода и первые 5 гармоник .

Для строки длиной $L$ с фиксированными концами, смещение $y(x,t)$ струны, перпендикулярной $x$-ось во времени $t$ является

$$y(x,t)=2y_{\text{max}}\sin(kx)\cos(2\pi ft),$$

где

• $y_{\text{max}}$ - амплитуда левых и правых бегущих волн, мешающих образованию стоячей волны,
• $k$ это волновое число ,
• $f$ это частота .

Частоты, которые резонируют и образуют стоячие волны, связаны с длиной струны следующим образом:

$$f={\frac {nv}{2L}},$$

$$n=1,2,3,\dots$$

где $v$ - скорость волны и целое число $n$ обозначает различные моды или гармоники . Стоячая волна с n = 1 колеблется на основной частоте и имеет длину волны, в два раза превышающую длину струны. Возможные формы колебаний образуют гармонический ряд .

Резонанс в сложных сетях

Обобщение на сложные сети связанных гармонических осцилляторов показывает, что такие системы имеют конечное число собственных резонансных частот, связанных с топологической структурой самой сети. В частности, такие частоты связаны с собственными значениями матрицы Лапласа сети. Позволять ${\bf {A}}$ — матрица смежности, описывающая топологическую структуру сети и ${\bf {L}}={\bf {K}}-{\bf {A}}$ соответствующую матрицу Лапласа , где ${\bf {K}}={\rm {diag}}\,\{k_{i}\}$ — диагональная матрица степеней узлов сети. Тогда для сети классических и идентичных гармонических осцилляторов, когда синусоидальная движущая сила $f(t)=F_{0}\sin \omega t$ применяется к конкретному узлу, глобальные резонансные частоты сети определяются выражением $\omega _{i}={\sqrt {1+\mu _{i}}}$ где $\mu _{i}$ являются собственными значениями лапласиана ${\bf {L}}$.

Типы

Механический и акустический

Основные статьи: Механический резонанс , Акустический резонанс и Струнный резонанс.

Школьный эксперимент с резонансной массой

Механический резонанс — это тенденция механической системы поглощать больше энергии, когда частота системы, ее колебаний соответствует собственной частоте вибрации чем на других частотах. Это может вызвать сильные раскачивания и даже катастрофические разрушения неправильно построенных конструкций, включая мосты, здания, поезда и самолеты. При проектировании объектов инженеры должны гарантировать, что частоты механического резонанса составных частей не совпадают с частотами движущих колебаний двигателей или других колеблющихся частей — явление, известное как резонансная катастрофа .

зданий, башен и мостов строительства Предотвращение резонансных катастроф является серьезной проблемой в каждом проекте . В качестве контрмеры можно установить амортизаторы для поглощения резонансных частот и, таким образом, рассеивания поглощенной энергии. В здании « Тайбэй 101» используется маятник массой 660 тонн (730 коротких тонн) — настроенный демпфер масс — для подавления резонанса. Более того, конструкция спроектирована так, чтобы резонировать на частоте, которая обычно не встречается. Здания в сейсмических зонах часто строятся с учетом частот колебаний ожидаемого движения грунта . Кроме того, инженеры, проектирующие объекты с двигателями, должны гарантировать, что механические резонансные частоты составных частей не совпадают с частотами движущих колебаний двигателей или других сильно колеблющихся частей.

Часы отсчитывают время посредством механического резонанса в балансовом колесе , маятнике или кристалле кварца .

Было высказано предположение, что частота шагов бегунов энергетически выгодна из-за резонанса между упругой энергией, запасенной в нижней конечности, и массой бегуна.

Акустический резонанс — это ветвь механического резонанса, которая связана с механическими вибрациями в диапазоне частот человеческого слуха, другими словами, звука . У людей слух обычно ограничен частотами от 20 Гц до 20 000 Гц (20 кГц ). Многие объекты и материалы действуют как резонаторы с резонансными частотами в этом диапазоне и при ударе механически вибрируют, толкая окружающий воздух, создавая звуковые волны. Это источник многих ударных звуков, которые мы слышим.

Акустический резонанс является важным фактором для производителей инструментов, поскольку в большинстве акустических инструментов используются резонаторы , такие как струны и корпус скрипки , длина трубки флейты , а также форма и натяжение мембраны барабана.

Как и механический резонанс, акустический резонанс может привести к катастрофическому выходу объекта из строя при резонансе. Классический пример — разбивание бокала со звуком точной резонансной частоты бокала, хотя на практике это сложно.

Международная космическая станция

Ракетные двигатели Международной космической станции (МКС) управляются автопилотом . Обычно загруженные параметры управления системой управления двигателями модуля «Звезда» заставляют ракетные двигатели вывести Международную космическую станцию ​​на более высокую орбиту. Ракетные двигатели шарнирно закреплены, и экипаж обычно не замечает их работы. Однако 14 января 2009 года загруженные параметры заставили автопилот раскачивать ракетные двигатели все сильнее и сильнее с частотой 0,5 Гц. Эти колебания были зафиксированы на видео и продолжались 142 секунды.

Электрика

Основная статья: Электрический резонанс

Анимация, иллюстрирующая электрический резонанс в настроенной цепи , состоящей из конденсатора (C) и катушки индуктивности (L), соединенных вместе. Заряд течет туда и обратно между пластинами конденсатора через индуктор. конденсатора Энергия колеблется взад и вперед между электрическим полем ( E индуктора ) и магнитным полем ( B ).

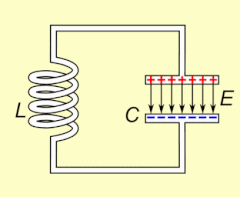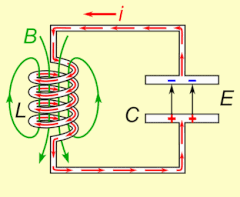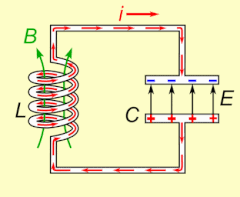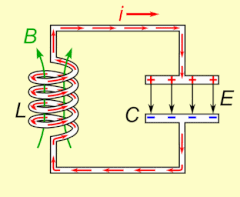
Электрический резонанс возникает в электрической цепи на определенной резонансной частоте , когда полное сопротивление цепи минимально в последовательной цепи или максимально в параллельной цепи (обычно, когда передаточная функция достигает максимума по абсолютному значению). Резонанс в цепях используется как для передачи, так и для приема беспроводной связи, такой как телевидение, сотовые телефоны и радио.

Оптический

Основная статья: Оптический резонатор

Оптический резонатор , также называемый оптическим резонатором , представляет собой систему зеркал , которая образует резонатор стоячей волны для световых волн . Оптические резонаторы являются основным компонентом лазеров , окружающим усиливающую среду и обеспечивающим обратную связь лазерного луча. Они также используются в оптических параметрических генераторах и некоторых интерферометрах . Свет, заключенный в полости, многократно отражается, создавая стоячие волны для определенных резонансных частот. Создаваемые модели стоячих волн называются «модами». Продольные моды различаются только по частоте, тогда как поперечные моды различаются для разных частот и имеют разную картину интенсивности по поперечному сечению пучка. Кольцевые резонаторы и шепчущие галереи являются примерами оптических резонаторов, не образующих стоячие волны.

Различные типы резонаторов различаются фокусными расстояниями двух зеркал и расстоянием между ними; плоские зеркала используются нечасто из-за сложности их точного выравнивания. Геометрию (тип резонатора) необходимо выбирать так, чтобы луч оставался стабильным, т. е. размер луча не продолжал расти с каждым отражением. Типы резонаторов также разработаны с учетом других критериев, таких как минимальная перетяжка луча или отсутствие фокусной точки (и, следовательно, интенсивного света в этой точке) внутри резонатора.

Оптические резонаторы спроектированы так, чтобы иметь очень добротность большую . Луч отражается большое количество раз с небольшим затуханием частотной , поэтому ширина линии луча мала по сравнению с частотой лазера.

Дополнительными оптическими резонансами являются резонансы направленной моды и поверхностный плазмонный резонанс , которые приводят к аномальному отражению и сильным затухающим полям при резонансе. В этом случае резонансными модами являются направленные моды волновода или поверхностные плазмонные моды границы раздела диэлектрик-металл. Эти моды обычно возбуждаются субволновой решеткой.

Орбитальный

Основная статья: Орбитальный резонанс

В небесной механике орбитальный резонанс возникает, когда два вращающихся тела оказывают регулярное, периодическое гравитационное влияние друг на друга, обычно из-за того, что их орбитальные периоды связаны соотношением двух небольших целых чисел. Орбитальные резонансы значительно усиливают взаимное гравитационное влияние тел. В большинстве случаев это приводит к нестабильному взаимодействию, при котором тела обмениваются импульсом и смещают орбиты до тех пор, пока резонанс не перестанет существовать. При некоторых обстоятельствах резонансная система может быть стабильной и самокорректирующейся, так что тела остаются в резонансе. Примерами являются резонанс 1:2:4 Юпитера спутников Ганимеда , Европы и Ио , а также резонанс 2:3 между Плутоном и Нептуном . Нестабильные резонансы с внутренними спутниками Сатурна приводят к образованию разрывов в кольцах Сатурна . Особый случай резонанса 1:1 (между телами с одинаковыми орбитальными радиусами) заставляет большие тела Солнечной системы очищать окрестности вокруг своих орбит, выбрасывая почти все остальное вокруг себя; этот эффект используется в текущем определение планеты .

Атомные, элементарные и молекулярные

Основные статьи: Ядерный магнитный резонанс и резонанс (физика элементарных частиц)

Магнит ЯМР в HWB-NMR, Бирмингем, Великобритания. В сильном поле 21,2 Тл протонный резонанс находится на частоте 900 МГц.

Ядерный магнитный резонанс (ЯМР) — это название явления физического резонанса, связанного с наблюдением специфических квантово-механических магнитных свойств атомного ядра в присутствии приложенного внешнего магнитного поля. Многие научные методы используют явления ЯМР для изучения молекулярной физики , кристаллов и некристаллических материалов посредством ЯМР-спектроскопии . ЯМР также обычно используется в передовых методах медицинской визуализации, таких как магнитно-резонансная томография (МРТ).

Все ядра, содержащие нечетное число нуклонов, обладают собственным магнитным моментом и угловым моментом . Ключевой особенностью ЯМР является то, что резонансная частота конкретного вещества прямо пропорциональна силе приложенного магнитного поля. Именно эта особенность используется в методах визуализации; если образец помещен в неоднородное магнитное поле, то резонансные частоты ядер образца зависят от того, в каком месте поля они расположены. Поэтому частицу можно довольно точно локализовать по ее резонансной частоте.

Электронный парамагнитный резонанс , также известный как электронный спиновый резонанс (ЭПР), представляет собой спектроскопический метод, аналогичный ЯМР, но вместо этого использует неспаренные электроны. Материалы, к которым это можно применить, гораздо более ограничены, поскольку материал должен одновременно иметь неспаренный спин и быть парамагнитным .

Эффект Мёссбауэра — это резонансное без отдачи излучение и поглощение гамма-квантов атомами, связанными в твердой форме.

Резонанс в физике элементарных частиц возникает при тех же обстоятельствах, что и в классической физике, на уровне квантовой механики и квантовой теории поля . Резонансы также можно рассматривать как нестабильные частицы, при этом формула, приведенная в разделе «Кривая универсального резонанса» статьи, применяется, если Γ частицы — скорость распада , а Ω — масса частицы M. этой частицы В этом случае формула исходит от пропагатора с заменой ее массы на комплексное число M + iΓ . Формула дополнительно связана со скоростью распада частицы оптической теоремой .

Недостатки

Колонна солдат, идущая ровным шагом по узкому и конструктивно гибкому мосту, может привести к его опасно большой амплитуды колебаниям . 12 апреля 1831 года подвесной мост Бротон недалеко от Солфорда, Англия, обрушился, когда по нему шла группа британских солдат. С тех пор в британской армии действует постоянный приказ солдатам сбавлять темп при марше по мостам, чтобы избежать резонанса от их обычного марша, влияющего на мост.

Вибрации двигателя или двигателя могут вызывать резонансные вибрации в его опорных конструкциях, если их собственная частота близка к частоте колебаний двигателя. Типичным примером является дребезжащий звук кузова автобуса, когда двигатель работает на холостом ходу.

Структурный резонанс подвесного моста, вызванный ветром, может привести к его катастрофическому обрушению. Несколько первых подвесных мостов в Европе и США были разрушены из-за структурного резонанса, вызванного умеренными ветрами. Обрушение моста через пролив Такома 7 ноября 1940 года характеризуется в физике как классический пример резонанса. и другие утверждали, Роберт Х. Сканлан что разрушение было вызвано аэроупругим флаттером , сложным взаимодействием между мостом и проходящим через него ветром — примером автоколебания или своего рода «самоподдерживающейся вибрации». ", как говорится в нелинейной теории вибраций.

Q-фактор

Основная статья: Q-фактор

Высокая и низкая добротность

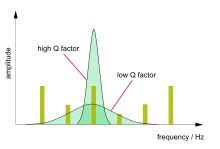
Добротность параметр, который описывает , или добротность — это безразмерный насколько затухает генератор или резонатор, и характеризует полосу пропускания резонатора относительно его центральной частоты. Высокое значение Q указывает на более низкую скорость потерь энергии по сравнению с запасенной энергией, т. е. система слегка демпфируется. Параметр определяется уравнением:

$$Q=2\pi {\text{ }}{\frac {\text{ maximum energy stored}}{\text{total energy lost per cycle at resonance}}}$$

.

Чем выше добротность, тем больше амплитуда на резонансной частоте и тем меньше полоса пропускания или диапазон частот вокруг резонанса. При электрическом резонансе цепь с высокой добротностью в радиоприемнике сложнее настроить, но она имеет большую избирательность и поэтому лучше фильтрует сигналы других станций. Генераторы с высокой добротностью более стабильны.

Примерами, которые обычно имеют низкий коэффициент добротности, являются дверные доводчики (Q=0,5). К системам с высокой добротностью относятся камертоны (Q=1000), атомные часы и лазеры (Q≈10 ¹¹ ).

Кривая

«Универсальная резонансная кривая», симметричное приближение к нормированному отклику резонансного контура; Значения по оси абсцисс представляют собой отклонение от центральной частоты в единицах центральной частоты, разделенных на 2Q; по ординате — относительная амплитуда и фаза в циклах; пунктирные кривые сравнивают диапазон срабатываний реальных двухполюсных цепей при значении Q, равном 5; для более высоких значений Q отклонение от универсальной кривой меньше. Крестиками отмечены края полосы пропускания 3 дБ (усиление 0,707, фазовый сдвиг 45° или цикл 0,125).

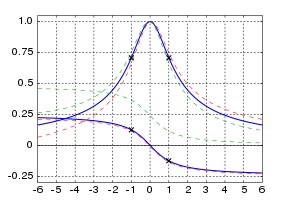
Точный отклик резонанса, особенно на частотах, далеких от резонансной частоты, зависит от деталей физической системы и обычно не совсем симметричен относительно резонансной частоты, как показано для простого гармонического генератора выше .Для слегка затухающего линейного генератора с резонансной частотой Ω интенсивность колебаний : I при движении системы с возбуждающей частотой ω обычно аппроксимируется формулой, симметричной относительно резонансной частоты

$$I(\omega )\equiv |\chi |^{2}\propto {\frac {1}{(\omega -\Omega )^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}.$$

Где восприимчивость $\chi (\omega )$ связывает амплитуду генератора с движущей силой в частотном пространстве:

$$x(\omega )=\chi (\omega )F(\omega )$$

Интенсивность определяется как квадрат амплитуды колебаний. Это функция Лоренца или распределение Коши , и этот отклик встречается во многих физических ситуациях, связанных с резонансными системами. Γ — параметр, зависящий от затухания генератора, известный как ширина линии резонанса. Сильно демпфированные генераторы, как правило, имеют широкую ширину линии и реагируют на более широкий диапазон возбуждающих частот вокруг резонансной частоты. Ширина линии обратно пропорциональна , добротности которая является мерой остроты резонанса.

В радиотехнике и электронике этот приблизительный симметричный отклик известен как универсальная резонансная кривая — концепция, введенная Фредериком Э. Терманом в 1932 году для упрощения приблизительного анализа радиосхем с диапазоном центральных частот и значений добротности .

См. также

• Киматика
• Приведенное гармоническое движение
• Сейсмостойкая инженерия
• Электрический дипольный спиновый резонанс
• Форманта
• Лимбический резонанс
• Нелинейный резонанс
• Обычный режим
• Положительный отзыв
• Шумановский резонанс
• Простое гармоническое движение
• Стохастический резонанс
• Симпатическая струна

Ссылки

• Аспельмейер, М ; Киппенберг, Тобиас Дж.; Марквардт, Флориан (30 декабря 2014 г.). «Резонаторная оптомеханика» . Обзоры современной физики . 86 (4): 1391. arXiv : 1303.0733 . Бибкод : 2014РвМП...86.1391А . дои : 10.1103/RevModPhys.86.1391 . hdl : 11858/00-001M-0000-002D-6464-3 . S2CID   119252645 .
• Биллах, К. Юсуф; Сканлан, Роберт Х (1991). «Резонанс, разрушение моста в Такоме и учебники физики для студентов» (PDF) . Американский журнал физики . 59 (2): 118–124. Бибкод : 1991AmJPh..59..118B . дои : 10.1119/1.16590 . Архивировано (PDF) из оригинала 19 сентября 2000 г. Проверено 1 января 2021 г.
• Гатак, Аджой (2005). Оптика (3-е изд.). Нью-Дели: Тата МакГроу-Хилл. ISBN  978-0-07-058583-6 .
• Холлидей, Дэвид ; Резник, Роберт ; Уокер, Джерл (2005). Основы физики . Том. часть 2 (7-е изд.). John Wiley & Sons Ltd. ISBN компании  978-0-471-71716-4 .
• Хардт, Дэвид (2004). «Понимание полюсов и нулей» (PDF) . 2.14 Анализ и проектирование систем управления с обратной связью . Массачусетский технологический институт . Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 18 апреля 2020 г.
• Харлоу, Джеймс Х., изд. (2004). Электротрансформаторостроение . Лондон: CRC Press. ISBN  978-0-8493-1704-0 .
• Огата, Кацухико (2005). Системная динамика (4-е изд.). Харлоу: Пирсон. ISBN  978-1-292-02608-4 .
• Олсон, Гарри Ф. (1967). Музыка, физика и инженерия . Том. 2. Нью-Йорк: Dover Publications. ISBN  978-0-486-21769-7 .
• Сервей, Раймонд А.; Фон, Джерри С. (1992). Колледж физики (3-е изд.). Издательство Колледжа Сондерса. ISBN  0-03-076377-0 .
• Зиберт, Уильям МакК. (1986). Цепи, сигналы и системы . Лондон; Нью-Йорк: Книжная компания McGraw Hill MIT Press. ISBN  978-0-262-19229-3 .
• Зигман, AE (1986). Лазеры . Университетские научные книги. ISBN  978-0-935702-11-8 .
• Снайдер, Кристин Л.; Фарли, Клэр Т. (2011). «Энергетически оптимальная частота шагов при беге: влияние наклона и снижения» . Журнал экспериментальной биологии . 214 (12): 2089–2095. дои : 10.1242/jeb.053157 . ПМИД   21613526 .
• Терман, Фредерик Эммонс (1932). Радиотехника (1-е изд.). Нью-Йорк: Книжная компания McGraw-Hill. OCLC   1036819790 .
• Тули, Майкл Х. (2006). Электронные схемы: основы и приложения . Оксфорд: Тейлор и Фрэнсис. ISBN  978-0-7506-6923-8 .

Внешние ссылки

• Фейнмановские лекции по физике Vol. Я Ч. 23: Резонанс
• Резонанс - глава из онлайн-учебника
• Грин, Брайан , « Резонанс в струнах ». Элегантная вселенная , NOVA ( PBS )
• Раздел гиперфизики, посвященный концепциям резонанса
• Резонанс против резонанса (употребление терминов)
• Древесный и воздушный резонанс в клавесине.
• Java-апплет, демонстрирующий резонансы струны при изменении частоты движущей силы
• Java-апплет, демонстрирующий возникновение резонанса, когда частота возбуждения совпадает с собственной частотой генератора.
• Разбивание стекла со звуком , включая высокоскоростную запись разбивания стекла.