График Боде

Рисунок 1А: Фильтр верхних частот (1-го порядка, однополюсный). График амплитуды Боде (вверху) и фазовый график Боде (внизу). Красная кривая данных аппроксимирована прямой черной линией.

Рисунок 1B: Фильтр нижних частот (1-го порядка, однополюсный). График амплитуды Боде (вверху) и график фазы Боде (внизу). Красная кривая данных аппроксимирована прямой черной линией.

В электротехнике и теории управления график Боде / ˈ b oʊ d i / представляет собой график частотной характеристики системы. Обычно это комбинация графика амплитуды Боде , выражающего величину (обычно в децибелах ) частотной характеристики, и фазового графика Боде , выражающего фазовый сдвиг .

Согласно первоначальной задумке Хендрика Уэйда Боде в 1930-х годах, график представляет собой асимптотическую аппроксимацию частотной характеристики с использованием отрезков прямых линий .

Обзор

Среди его нескольких важных вкладов в теорию цепей и теорию управления инженер Хендрик Уэйд Боде , работая в Bell Labs в 1930-х годах, разработал простой, но точный метод построения графиков усиления и фазового сдвига. Они носят его имя: график усиления Боде и фазовый график Боде . «Боде» часто произносится / ˈ b oʊ d i / BOH -dee , хотя голландское произношение Голландский: [ˈboːdə] BOH -duh .

Боде столкнулся с проблемой разработки стабильных усилителей с обратной связью для использования в телефонных сетях. Он разработал метод графического проектирования графиков Боде, чтобы показать запас по усилению и запас по фазе, необходимый для поддержания стабильности при изменениях характеристик схемы, возникающих во время производства или во время эксплуатации. Разработанные принципы были применены к задачам проектирования следящих механизмов и других систем управления с обратной связью. График Боде является примером анализа в частотной области .

Определение

График Боде для линейной, постоянной во времени системы с передаточной функцией $H(s)$ ( $s$ будучи комплексной частотой в области Лапласа ) состоит из графика величины и графика фазы.

График величины Боде представляет собой график функции $|H(s=j\omega )|$ частоты $\omega$ (с $j$ мнимая единица ). $\omega$-ось графика магнитуды логарифмическая, а магнитуда указана в децибелах , т. е. значение магнитуды $|H|$ откладывается на оси в $20\log _{10}|H|$.

Фазовый график Боде представляет собой график фазы передаточной функции, обычно выражаемой в градусах. $\arg \left(H(s=j\omega )\right)$ как функция $\omega$. Фаза отображается в том же логарифмическом виде. $\omega$-ось в качестве графика величины, но значение фазы отображается на линейной вертикальной оси.

Частотная характеристика

В этом разделе показано, что график Боде представляет собой визуализацию частотной характеристики системы.

Рассмотрим линейную стационарную систему с передаточной функцией $H(s)$. Предположим, что на систему воздействует синусоидальный входной сигнал с частотой $\omega$,

$u(t)=\sin(\omega t),$

который применяется настойчиво, т.е. время от времени $-\infty$ до времени $t$. Ответ будет иметь вид

$y(t)=y_{0}\sin(\omega t+\varphi ),$

т. е. также синусоидальный сигнал с амплитудой $y_{0}$ сдвинутый на фазу $\varphi$ относительно ввода.

Это можно показать что величина ответа

$y_{0}=|H(\mathrm {j} \omega )|$ ( 1 )

и что фазовый сдвиг

$\varphi =\arg H(\mathrm {j} \omega ).$ ( 2 )

Таким образом, при воздействии с частотой $\omega$, система реагирует на той же частоте выходным сигналом, который усиливается в коэффициент $|H(\mathrm {j} \omega )|$ и сдвинут по фазе на $\arg H(\mathrm {j} \omega )$. Таким образом, эти величины характеризуют частотную характеристику и отображаются на графике Боде.

Правила построения сюжета Боде своими руками

Для многих практических задач подробные графики Боде можно аппроксимировать отрезками прямых, которые являются асимптотами точного отклика. Влияние каждого из членов многоэлементной передаточной функции можно аппроксимировать набором прямых линий на графике Боде. Это позволяет графически решить общую функцию частотной характеристики. До широкого распространения цифровых компьютеров широко использовались графические методы, чтобы уменьшить необходимость утомительных вычислений; графическое решение может быть использовано для определения возможных диапазонов параметров новой конструкции.

Суть графика Боде заключается в том, что можно рассматривать журнал функции в виде

$f(x)=A\prod (x-c_{n})^{a_{n}}$

как сумма логарифмов его нулей и полюсов :

$\log(f(x))=\log(A)+\sum a_{n}\log(x-c_{n}).$

Эта идея явно используется в методе построения фазовых диаграмм. Метод построения графиков амплитуд неявно использует эту идею, но поскольку логарифм амплитуды каждого полюса или нуля всегда начинается с нуля и имеет только одно изменение асимптоты (прямые линии), метод можно упростить.

Прямолинейный график амплитуды

Амплитуда в децибелах обычно определяется с помощью ${\text{dB}}=20\log _{10}(X)$ определить децибелы. Учитывая передаточную функцию в виде

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}},$

где $x_{n}$ и $y_{n}$ являются константами, $s=\mathrm {j} \omega$, $a_{n},b_{n}>0$, и $H$ передаточная функция:

• При каждом значении s где $\omega =x_{n}$ (ноль), увеличьте наклон линии на $20a_{n}\ {\text{dB}}$ за десятилетие .
• При каждом значении s где $\omega =y_{n}$ (столб), уменьшите наклон линии на $20b_{n}\ {\text{dB}}$ за десятилетие.
• Начальное значение графа зависит от границ. Начальную точку можно найти, положив начальную угловую частоту $\omega$ в функцию и найти $|H(\mathrm {j} \omega )|$.
• Начальный наклон функции при начальном значении зависит от количества и порядка нулей и полюсов, находящихся при значениях ниже начального значения, и находится с помощью первых двух правил.

Для обработки неприводимых полиномов 2-го порядка: $ax^{2}+bx+c$ во многих случаях может быть аппроксимировано как $({\sqrt {a}}x+{\sqrt {c}})^{2}$.

Обратите внимание, что нули и полюса возникают, когда $\omega$ равен ​ определенному $x_{n}$ или $y_{n}$. Это связано с тем, что рассматриваемая функция представляет собой величину $H(\mathrm {j} \omega )$, и поскольку это сложная функция, $|H(\mathrm {j} \omega )|={\sqrt {H\cdot H^{*}}}$. Таким образом, в любом месте, где есть ноль или полюс, включающий член $(s+x_{n})$, величина этого члена равна ${\sqrt {(x_{n}+\mathrm {j} \omega )(x_{n}-\mathrm {j} \omega )}}={\sqrt {x_{n}^{2}+\omega ^{2}}}$.

График скорректированной амплитуды

Чтобы исправить прямолинейный график амплитуды:

• У каждого нуля ставим точку $3a_{n}\ {\text{dB}}$ над линией.
• На каждом полюсе поставьте точку $3b_{n}\ {\text{dB}}$ ниже линии.
• Нарисуйте плавную кривую через эти точки, используя прямые линии в качестве асимптот (линии, к которым приближается кривая).

Обратите внимание, что этот метод коррекции не включает обработку комплексных значений $x_{n}$ или $y_{n}$. В случае неприводимого полинома лучший способ исправить график — это фактически вычислить величину передаточной функции в полюсе или нуле, соответствующую неприводимому полиному, и поставить эту точку над или под линией в этом полюсе или нуле. .

Прямолинейный фазовый график

Учитывая передаточную функцию в той же форме, что и выше,

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}},$

идея состоит в том, чтобы нарисовать отдельные графики для каждого полюса и нуля, а затем сложить их. Фактическая фазовая кривая определяется выражением

$\varphi (s)=-\arctan {\frac {\operatorname {Im} [H(s)]}{\operatorname {Re} [H(s)]}}.$

Чтобы нарисовать фазовый график для каждого полюса и нуля:

• Если $A$ положителен, стартовая линия (с нулевым наклоном) равна 0°.
• Если $A$ отрицательна, стартовая линия (с нулевым наклоном) равна -180°.
• Если сумма количества нестабильных нулей и полюсов нечетна, прибавьте к этому базису 180°.
• Каждый раз $\omega =|x_{n}|$ (для устойчивых нулей $-\operatorname {Re} (z)<0$), увеличить наклон на $45a_{n}$ градусов за десятилетие, начиная с десятилетия назад $\omega =|x_{n}|$ (например, $|x_{n}|/10$).
• Каждый раз $\omega =|y_{n}|$ (для устойчивых опор $-\operatorname {Re} (p)<0$), уменьшите наклон на $45b_{n}$ градусов за десятилетие, начиная с десятилетия назад $\omega =|y_{n}|$ (например, $|y_{n}|/10$).
• «Нестабильные» (правая полуплоскость) полюса и нули ( $\operatorname {Re} (s)>0$) имеют противоположное поведение.
• Снова сгладьте наклон, когда фаза изменится на $90a_{n}$ градусов (для нуля) или $90b_{n}$ градусов (для полюса).
• После построения одной линии для каждого полюса или нуля сложите линии вместе, чтобы получить окончательный фазовый график; то есть график последней фазы представляет собой суперпозицию каждого графика предыдущей фазы.

Пример

Чтобы построить прямолинейный график для фильтра нижних частот первого порядка (однополюсного), рассматривается нормированная форма передаточной функции через угловую частоту:

$H_{\text{lp}}(\mathrm {j} \omega )={\frac {1}{1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}}}.$

График Боде показан на рисунке 1(b) выше, а построение линейной аппроксимации обсуждается далее.

График магнитуды

Величина (в децибелах ) приведенной выше передаточной функции (нормализованная и преобразованная в форму угловой частоты), определяемая выражением усиления в децибелах. $A_{\text{vdB}}$:

${\begin{aligned}A_{\text{vdB}}&=20\log |H_{\text{lp}}(\mathrm {j} \omega )|\\&=20\log {\frac {1}{\left|1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}\right|}}\\&=-20\log \left|1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}\right|\\&=-10\log \left(1+{\frac {\omega ^{2}}{\omega _{\text{c}}^{2}}}\right).\end{aligned}}$

Затем построили график зависимости входной частоты. $\omega$ в логарифмическом масштабе может быть аппроксимирован двумя линиями , образующими асимптотический (приблизительный) график Боде по величине передаточной функции:

• Первая строка для угловых частот ниже $\omega _{\text{c}}$ представляет собой горизонтальную линию на уровне 0 дБ, поскольку на низких частотах $\omega /\omega _{\text{c}}$ Этот член мал, и им можно пренебречь, в результате чего приведенное выше уравнение усиления децибел будет равно нулю.
• Вторая строка для угловых частот выше $\omega _{\text{c}}$ представляет собой линию с наклоном −20 дБ за декаду, поскольку на высоких частотах $\omega /\omega _{\text{c}}$ термин доминирует, и приведенное выше выражение усиления в децибелах упрощается до $-20\log(\omega /\omega _{\text{c}})$, который представляет собой прямую линию с наклоном −20 дБ за декаду.

Эти две линии встречаются на угловой частоте $\omega _{\text{c}}$. Из графика видно, что для частот значительно ниже угловой частоты схема имеет затухание 0 дБ, что соответствует единичному коэффициенту усиления полосы пропускания, т. е. амплитуда выходного сигнала фильтра равна амплитуде входного сигнала. Частоты выше угловой частоты ослабляются – чем выше частота, тем выше затухание .

Фазовый график

Фазовый график Боде получается путем построения фазового угла передаточной функции, определяемой выражением

$\arg H_{\text{lp}}(\mathrm {j} \omega )=-\tan ^{-1}{\frac {\omega }{\omega _{\text{c}}}}$

против $\omega$, где $\omega$ и $\omega _{\text{c}}$ — входная и граничная угловые частоты соответственно. Для входных частот, намного меньших угловых, соотношение $\omega /\omega _{\text{c}}$ мала, поэтому фазовый угол близок к нулю. С увеличением отношения абсолютное значение фазы увеличивается и становится -45°, когда $\omega =\omega _{\text{c}}$. По мере увеличения соотношения для входных частот, намного превышающих угловую частоту, фазовый угол асимптотически приближается к -90°. Частотная шкала фазового графика является логарифмической.

Нормализованный график

Горизонтальная ось частот как на графике амплитуды, так и на фазовом графике может быть заменена нормализованным (безразмерным) отношением частот. $\omega /\omega _{\text{c}}$. В таком случае говорят, что график нормализован, и единицы измерения частот больше не используются, поскольку все входные частоты теперь выражаются как кратные частоте среза. $\omega _{\text{c}}$.

Пример с нулем и полюсом

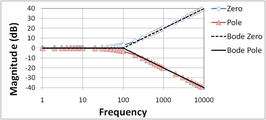
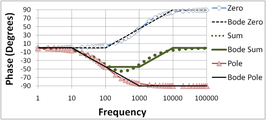
Рисунки 2-5 дополнительно иллюстрируют построение графиков Боде. Этот пример с полюсом и нулем показывает, как использовать суперпозицию. Для начала компоненты представлены отдельно.

На рисунке 2 показан график величины Боде для нулевого и низкочастотного полюса, а также их сравнение с прямыми графиками Боде. Прямолинейные графики горизонтальны до положения полюса (нуля), а затем падают (поднимаются) со скоростью 20 дБ/декада. Второй рисунок 3 делает то же самое для фазы. Фазовые графики горизонтальны до частотного коэффициента в десять ниже положения полюса (нуля), а затем падают (поднимаются) на 45°/декаду, пока частота не станет в десять раз выше, чем положение полюса (нуля). Затем графики снова становятся горизонтальными на более высоких частотах с окончательным полным изменением фазы на 90 °.

На рисунках 4 и 5 показано, как осуществляется суперпозиция (простое сложение) графика полюса и нуля. Прямые графики Боде снова сравниваются с точными графиками. Ноль был перенесен на более высокую частоту, чем полюс, чтобы сделать пример более интересным. Обратите внимание, что на рисунке 4 падение полюса на 20 дБ/декада сдерживается повышением нуля на 20 дБ/декада, что приводит к построению горизонтального графика магнитуды для частот выше нулевого местоположения. Обратите внимание на рисунке 5 на фазовом графике, что линейное приближение довольно приблизительное в области, где и полюс, и ноль влияют на фазу. Также обратите внимание на рисунок 5, что диапазон частот, где изменяется фаза на прямолинейном графике, ограничен частотами в десять раз выше и ниже положения полюса (нуля). Там, где присутствуют и фаза полюса, и ноль, прямолинейный фазовый график является горизонтальным, поскольку падение полюса на 45 °/декаду останавливается перекрывающимся подъемом нуля на 45 °/декаду в ограниченном диапазоне частот. где оба являются активными участниками фазы.

• Пример с полюсом и нулем
• 
  Рисунок 2: График величины Боде для нулевого и низкочастотного полюса; кривые с надписью «Боде» представляют собой прямолинейные графики Боде.
• 
  Рисунок 3: Фазовый график Боде для нулевого и низкочастотного полюса; кривые с надписью «Боде» представляют собой прямолинейные графики Боде.
• 
  Рисунок 4: График величины Боде для комбинации полюс-ноль; расположение нуля в десять раз выше, чем на рисунках 2 и 3; кривые с надписью «Боде» представляют собой прямолинейные графики Боде.
• 
  Рисунок 5: Фазовый график Боде для комбинации полюс-ноль; расположение нуля в десять раз выше, чем на рисунках 2 и 3; кривые с надписью «Боде» представляют собой прямолинейные графики Боде.

усиления и запас

См. также: Запас по фазе

Графики Боде используются для оценки стабильности усилителей с отрицательной обратной связью путем определения запаса усиления и фазы усилителя. Понятие коэффициента усиления и запаса по фазе основано на выражении усиления для усилителя с отрицательной обратной связью, определяемом выражением

$A_{\text{FB}}={\frac {A_{\text{OL}}}{1+\beta A_{\text{OL}}}},$

где A _FB — коэффициент усиления усилителя с обратной связью ( коэффициент усиления с обратной связью ), β — коэффициент обратной связи , а A _OL — коэффициент усиления без обратной связи ( коэффициент усиления с разомкнутым контуром ). Коэффициент усиления A _OL представляет собой сложную функцию частоты, имеющую как величину, так и фазу. Исследование этого соотношения показывает возможность бесконечного выигрыша (интерпретируемого как нестабильность), если произведение β A _OL = −1 (т. е. величина β A _OL равна единице, а его фаза равна −180°, так называемая устойчивость Баркгаузена критерий ). Графики Боде используются для определения того, насколько близок усилитель к удовлетворению этого условия.

Ключом к этому определению являются две частоты. Первый, обозначенный здесь как f ₁₈₀ , представляет собой частоту, на которой коэффициент усиления разомкнутого контура меняет знак. Второй, обозначенный здесь f _{0 дБ} , представляет собой частоту, на которой величина произведения |β A _OL | = 1 = 0 дБ. То есть частота f ₁₈₀ определяется условием

$\beta A_{\text{OL}}(f_{180})=-|\beta A_{\text{OL}}(f_{180})|=-|\beta A_{\text{OL}}|_{180},$

где вертикальные черточки обозначают величину комплексного числа , а частота f _{0 дБ} определяется условием

$|\beta A_{\text{OL}}(f_{\text{0 dB}})|=1.$

Одним из показателей близости к нестабильности является запас усиления . Фазовый график Боде определяет частоту, на которой фаза β A _OL достигает -180°, обозначенную здесь как частота f ₁₈₀ . Используя эту частоту, график величины Боде находит величину β A _OL . Если |β A _OL | ₁₈₀ ≥ 1, как уже упоминалось, усилитель неустойчив. Если |β A _OL | ₁₈₀ < 1 нестабильности не происходит, и разделение в дБ по величине |β A _OL | ₁₈₀ от |β A _OL | = 1 называется запасом усиления . Поскольку величина 1 равна 0 дБ, запас усиления представляет собой одну из эквивалентных форм: $20\log _{10}|\beta A_{\text{OL}}|_{180}=20\log _{10}|A_{\text{OL}}|-20\log _{10}\beta ^{-1}$.

Другой эквивалентной мерой близости к нестабильности является запас по фазе . График Боде определяет частоту, на которой величина |β A _OL | достигает единицы, обозначенной здесь как частота f _{0 дБ} . Используя эту частоту, фазовый график Боде находит фазу β A _OL . Если фаза β A _OL ( f _{0 дБ} ) > −180°, условие нестабильности не может быть выполнено ни на какой частоте (поскольку его величина будет < 1 при f = f ₁₈₀ ), а расстояние фазы при f _{0 дБ} в градусах выше −180° называется запасом по фазе .

Если достаточно просто ответить «да» или «нет» по вопросу стабильности, то усилитель стабилен, если f _{0 дБ} < f ₁₈₀ . Этого критерия достаточно для прогнозирования стабильности только для усилителей, удовлетворяющих некоторым ограничениям на положение полюса и нуля ( системы с минимальной фазой ). Хотя эти ограничения обычно соблюдаются, в противном случае необходимо использовать другой метод, например график Найквиста . Оптимальные запасы по усилению и фазе можно рассчитать с использованием теории интерполяции Неванлинны – Пика .

Примеры использования графиков Боде

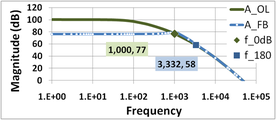
Рисунки 6 и 7 иллюстрируют поведение коэффициента усиления и терминологию. Для трехполюсного усилителя на рисунке 6 сравнивается график Боде для коэффициента усиления без обратной связи ( коэффициент усиления с разомкнутым контуром ) A _OL с коэффициентом усиления с обратной связью A _FB ( коэффициент усиления с обратной связью ). см. в разделе «Усилитель с отрицательной обратной связью» Более подробную информацию .

В данном примере A _OL = 100 дБ на низких частотах и ​​1/β = 58 дБ. На низких частотах A _FB также ≈ 58 дБ.

Поскольку на графике отображается коэффициент усиления разомкнутого контура A _OL , а не произведение β A _OL , условие A _OL = 1/β определяет f _{0 дБ} . Коэффициент усиления обратной связи на низких частотах и ​​при большом коэффициенте усиления A _OL равен A _FB ≈ 1/β (см. формулу коэффициента усиления обратной связи в начале этого раздела для случая большого коэффициента усиления A _OL ), поэтому эквивалентный способ найти f _{0 дБ} означает, что коэффициент усиления обратной связи пересекает коэффициент усиления разомкнутого контура. (Частота f _{0 дБ} потребуется позже для определения запаса по фазе.)

Вблизи этого пересечения двух коэффициентов усиления при f _{0 дБ} критерии Баркгаузена в этом примере почти удовлетворяются, а усилитель с обратной связью демонстрирует огромный пик усиления (он был бы бесконечен, если бы β A _OL = −1). За пределами частоты единичного усиления f _{0 дБ} усиление в разомкнутом контуре достаточно мало, что A _FB ≈ A _OL (рассмотрите формулу в начале этого раздела для случая малого A _OL ).

На рисунке 7 показано соответствующее сравнение фаз: фаза усилителя обратной связи близка к нулю до частоты f ₁₈₀ , где коэффициент усиления в разомкнутом контуре имеет фазу -180°. В этой области фаза усилителя обратной связи резко падает вниз и становится почти такой же, как фаза усилителя с разомкнутым контуром. (Напомним, A _FB ≈ A _OL для маленького A _OL .)

Сравнивая отмеченные точки на рисунках 6 и 7, видно, что частота единичного усиления f _{0 дБ} и частота переворота фазы f ₁₈₀ в этом усилителе практически равны: f ₁₈₀ ≈ f _{0 дБ} ≈ 3,332 кГц, что означает запас по усилению и запас по фазе практически равны нулю. Усилитель практически стабилен.

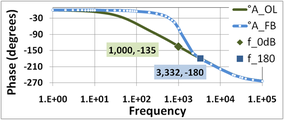
На рисунках 8 и 9 показаны запас по усилению и запас по фазе для различной величины обратной связи β. Коэффициент обратной связи выбирается меньшим, чем на рисунке 6 или 7, сдвигая условие | β А _ОЛ | = 1 для понижения частоты. В данном примере 1/β = 77 дБ, а на низких частотах A _FB ≈ 77 дБ.

На рисунке 8 показан график усиления. Из рисунка 8 видно, что пересечение 1/β и A _OL происходит при f _{0 дБ} = 1 кГц. Обратите внимание, что пик усиления A _FB вблизи f _{0 дБ} почти исчез.

Рисунок 9 представляет собой фазовый график. Используя значение f _{0 дБ} = 1 кГц, полученное выше из графика амплитуды на рисунке 8, фаза разомкнутого контура при f _{0 дБ} составляет -135°, что представляет собой запас по фазе на 45° выше -180°.

Используя рисунок 9, для фазы −180° значение f ₁₈₀ = 3,332 кГц (конечно, тот же результат, что и ранее полученный ). Усиление разомкнутого контура на рисунке 8 при f ₁₈₀ составляет 58 дБ, а 1/β = 77 дБ, поэтому запас по усилению составляет 19 дБ.

Стабильность не является единственным критерием отклика усилителя, и во многих приложениях более строгим требованием, чем стабильность, является хорошая реакция на скачок . Как правило , для хорошей реакции на скачок требуется запас по фазе не менее 45°, и часто рекомендуется запас более 70°, особенно там, где изменение компонентов из-за производственных допусков является проблемой. См. также обсуждение запаса по фазе в статье о переходном процессе .

• Примеры
• 
  Рисунок 6: Коэффициент усиления усилителя обратной связи A _FB в дБ и соответствующего усилителя с разомкнутым контуром A _OL . Параметр 1/β = 58 дБ, а на низких частотах A _FB ≈ 58 дБ. Запас усиления в этом усилителе почти равен нулю, поскольку | β А _ОЛ | = 1 происходит почти при f = f _180° .
• 
  Рисунок 7: Фаза усилителя обратной связи °A _FB в градусах и соответствующего усилителя с разомкнутым контуром °A _OL . Запас по фазе в этом усилителе почти равен нулю, поскольку переворот фазы происходит почти при единичной частоте усиления f = f _{0 дБ} , где | β А _ОЛ | = 1.
• 
  Рисунок 8: Коэффициент усиления усилителя обратной связи A _FB в дБ и соответствующего усилителя с разомкнутым контуром A _OL . В этом примере 1/β = 77 дБ. Запас усиления в этом усилителе составляет 19 дБ.
• 
  Рисунок 9: Фаза усилителя обратной связи A _FB в градусах и соответствующего усилителя с разомкнутым контуром A _OL . Запас по фазе в этом усилителе составляет 45°.

Плоттер Боде

Рисунок 10: Амплитудная диаграмма электронного фильтра 10-го порядка , построенная с помощью графопостроителя Боде.

Плоттер Боде — это электронный инструмент, напоминающий осциллограф , который создает диаграмму Боде или график коэффициента усиления напряжения или фазового сдвига схемы в зависимости от частоты в системе управления с обратной связью или фильтре. Пример этого показан на рисунке 10. Он чрезвычайно полезен для анализа и тестирования фильтров и стабильности систем управления с обратной связью посредством измерения угловых частот (граничных частот), а также запасов усиления и фазы.

Это идентично функции, выполняемой векторным анализатором цепей , но анализатор цепей обычно используется на гораздо более высоких частотах.

В образовательных и исследовательских целях построение диаграмм Боде для заданных передаточных функций способствует лучшему пониманию и более быстрому получению результатов (см. Внешние ссылки).

Связанные сюжеты

Основные статьи: сюжет Найквиста и сюжет Николса

Два связанных графика, которые отображают одни и те же данные в разных системах координат, — это график Найквиста и график Николса . Это параметрические графики с частотой в качестве входных данных и величиной и фазой частотной характеристики в качестве выходных данных. График Найквиста отображает их в полярных координатах с отображением величины на радиус и фазу на аргумент (угол). На графике Николса они отображаются в прямоугольных координатах в логарифмическом масштабе .

• 
  Рисунок 11: График Найквиста .
• 
  Рисунок 12: График Николса того же ответа, что и на рисунке 11.

См. также

• Аналоговая обработка сигналов
• Запас по фазе
• Интеграл чувствительности Боде
• Отношение величины (усиления) Боде к фазе
• Электрохимическая импедансная спектроскопия

Внешние ссылки

• Как рисовать кусочно-асимптотические графики Боде
• Код Gnuplot для создания графика Боде: шаблон для печати DIN-A4 (pdf)