Маятник

Маятник – это устройство, состоящее из груза, подвешенного к шарниру так, что оно может свободно качаться. [1] Когда маятник смещается в сторону от своего положения покоя, равновесия , на него действует восстанавливающая сила гравитации , которая ускоряет его обратно к положению равновесия. При отпускании восстанавливающая сила, действующая на массу маятника, заставляет его колебаться около положения равновесия, раскачиваясь вперед и назад. Время одного полного цикла, левого и правого колебаний, называется периодом . Период зависит от длины маятника, а также в некоторой степени от амплитуды , ширины качания маятника.
Регулярное движение маятников использовалось для измерения времени и было самой точной технологией измерения времени в мире до 1930-х годов. [2] Маятниковые часы, изобретенные Христианом Гюйгенсом в 1656 году, стали мировым стандартом хронометриста, использовались в домах и офисах в течение 270 лет и достигали точности около одной секунды в год, прежде чем их заменили в качестве эталона времени кварцевые часы в 1930-х годах . Маятники также используются в научных приборах, таких как акселерометры и сейсмометры . Исторически они использовались в качестве гравиметров для измерения ускорения силы тяжести при геофизических исследованиях и даже в качестве эталона длины. Слово «маятник» — неолатинское , от латинского pendulus , что означает « подвешивание » . [3]
Простой гравитационный маятник [ править ]
Простой гравитационный маятник [4] представляет собой идеализированную математическую модель маятника. [5] [6] [7] Это груз (или боб ) на конце невесомого шнура подвешенного на шарнире , без трения . При первом толчке он будет раскачиваться вперед и назад с постоянной амплитудой . Настоящие маятники подвержены трению и сопротивлению воздуха , поэтому амплитуда их колебаний уменьшается.
Период колебаний [ править ]
Период качания простого гравитационного маятника зависит от его длины , местной силы тяжести и в небольшой степени от максимального угла , на который маятник отклоняется от вертикали, θ 0 , называемого амплитудой . [8] Это не зависит от массы боба. Если амплитуда ограничена небольшими колебаниями, [Примечание 1] период Т : простого маятника, время, необходимое для полного цикла, равен [9]
| ( 1 ) |
где длина маятника и - местное ускорение силы тяжести .
Для небольших колебаний период колебаний примерно одинаков для колебаний разного размера: то есть период не зависит от амплитуды . Это свойство, называемое изохронизмом , является причиной того, что маятники так полезны для измерения времени. [10] Последовательные колебания маятника, даже меняющиеся по амплитуде, занимают одинаковое количество времени.
Для больших амплитуд период постепенно увеличивается с амплитудой, поэтому он больше, чем определяется уравнением (1). Например, при амплитуде θ 0 = 0,4 радиана (23°) это на 1% больше, чем дает формула (1). Период асимптотически увеличивается (до бесконечности) по мере приближения θ 0 к π радиан (180°), поскольку значение θ 0 = π является неустойчивой точкой равновесия маятника. Истинный период идеального простого гравитационного маятника можно записать в нескольких различных формах (см. маятник (механика) ), одним из примеров является бесконечный ряд : [11] [12]
Разница между этим истинным периодом и периодом небольших колебаний (1), указанным выше, называется круговой ошибкой . В случае типичных напольных часов, маятник которых имеет поворот 6° и, следовательно, амплитуду 3° (0,05 радиан), разница между истинным периодом и приближением малого угла (1) составляет около 15 секунд в день.
При небольших колебаниях маятник приближается к гармоническому осциллятору , и его движение как функция времени t представляет собой приблизительно простое гармоническое движение : [5]
Для настоящих маятников период немного варьируется в зависимости от таких факторов, как плавучесть и вязкое сопротивление воздуха, масса нити или стержня, размер и форма качания и способ его прикрепления к веревке, а также гибкость и растяжение маятника. строка. [11] [13] В прецизионных приложениях может потребоваться внесение поправок на эти факторы в уравнение. (1) точно указать период.
Затухающий приводной маятник представляет собой хаотическую систему. [ нужна ссылка ]
Сложный маятник [ править ]
Любое качающееся твердое тело, свободно вращающееся вокруг неподвижной горизонтальной оси, называется составным маятником или физическим маятником . Сложный маятник имеет тот же период, что и простой гравитационный маятник длиной , называемая эквивалентной длиной или радиусом колебания , равная расстоянию от оси вращения до точки, называемой центром колебания . [14] Эта точка расположена под центром масс маятника, на расстоянии, которое зависит от распределения массы маятника. Если большая часть массы сосредоточена в относительно небольшом шарике по сравнению с длиной маятника, центр колебаний будет близок к центру масс. [15]
Радиус колебания или эквивалентная длина можно показать, что любой физический маятник
где - момент инерции маятника относительно точки поворота , - общая масса маятника, а — расстояние между точкой поворота и центром масс .Подставив это выражение в (1) выше, период составного маятника определяется выражением
Например, жесткий однородный стержень длиной повернутый вокруг одного конца имеет момент инерции . Центр масс расположен в центре стержня, поэтому Подстановка этих значений в приведенное выше уравнение дает . Это показывает, что маятник с жестким стержнем имеет тот же период, что и простой маятник, составляющий две трети его длины.
Христиан Гюйгенс доказал в 1673 году, что точка поворота и центр колебаний взаимозаменяемы. [17] Это означает, что если какой-либо маятник перевернуть и качнуть от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, и новый центр колебаний будет в старой точке вращения. В 1817 году Генри Катер использовал эту идею для создания обратимого маятника, теперь известного как маятник Катера , для улучшения измерения ускорения свободного падения.
История [ править ]

Одним из первых известных применений маятника был сейсмометр I века , созданный из династии Хань китайским ученым Чжан Хэном . [18] Его функция заключалась в том, чтобы раскачивать и активировать один из ряда рычагов после того, как его потревожило землетрясение вдалеке . [19] Высвобожденный рычагом, небольшой шарик выпадал из устройства в форме урны в одну из восьми пастей металлических жаб внизу, в восьми точках компаса, обозначая направление, в котором произошло землетрясение. [19]
Множество источников [20] [21] [22] [23] утверждают, что египетский астроном X века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году у британского историка Эдварда Бернарда . [24] [25] [26] [27]
В эпоху Возрождения большие маятники с ручным насосом использовались в качестве источников энергии для ручных возвратно-поступательных машин, таких как пилы, сильфоны и насосы. [28] Леонардо да Винчи сделал множество рисунков движения маятников, хотя и не осознавал его значения для измерения времени.
Галилея исследования 1602 :
Итальянский учёный Галилео Галилей первым начал изучать свойства маятников, начиная примерно с 1602 года. [29] Первое упоминание об интересе к маятникам, проявленное Галилеем, относится примерно к 1588 году в его посмертно опубликованных заметках под названием « О движении» . [30] [31] в котором он отметил, что более тяжелые объекты будут продолжать колебаться большее время, чем более легкие. Самый ранний из сохранившихся отчетов о его экспериментальных исследованиях содержится в письме Гвидо Убальдо даль Монте из Падуи от 29 ноября 1602 года. [32] Его биограф и ученик Винченцо Вивиани утверждал, что его интерес возник примерно в 1582 году благодаря раскачиванию люстры в Пизанском соборе . [33] [34] Галилей обнаружил важнейшее свойство, которое делает маятники полезными в качестве хронометристов, — изохронизм; период маятника примерно не зависит от амплитуды или ширины качания. [35] Он также обнаружил, что период не зависит от массы груза и пропорционален квадратному корню из длины маятника. Он впервые применил свободно раскачивающиеся маятники в простых приложениях для измерения времени. Санторио Сантори пациента в 1602 году изобрел устройство, измеряющее пульс по длине маятника; пульсилогиум . [36] В 1641 году Галилей продиктовал своему сыну Винченцо проект механизма, поддерживающего колебание маятника, который был описан как первые часы с маятником; [35] Винченцо начал строительство, но не завершил его, когда умер в 1649 году. [37]
: Часы маятником с 1656
В 1656 году голландский учёный Христиан Гюйгенс построил первые маятниковые часы . [38] Это было большим улучшением по сравнению с существующими механическими часами; их лучшая точность была улучшена с отклонения примерно с 15 минут в день до примерно 15 секунд в день. [39] Маятники распространились по Европе, поскольку были модернизированы существующие часы. ими [40]
Примерно в 1666 году английский учёный Роберт Гук изучил конический маятник , состоящий из маятника, который мог свободно качаться в двух измерениях, с качанием, вращающимся по кругу или эллипсу. [41] использовал движения этого устройства в качестве модели для анализа орбитальных движений планет Он . [42] Гук предположил Исааку Ньютону в 1679 году, что компоненты орбитального движения состоят из инерционного движения по касательной плюс движения притяжения в радиальном направлении. Это сыграло роль в формулировке Ньютоном закона всемирного тяготения . [43] [44] Роберт Гук также был ответственен за предположение еще в 1666 году о том, что маятник можно использовать для измерения силы гравитации. [41]
Во время своей экспедиции в Кайенну , Французская Гвиана , в 1671 году Жан Рише обнаружил, что часы маятниковые На 2 + 1 ⁄ . минуты в день медленнее в Кайенне, чем в Париже Из этого он пришел к выводу, что сила тяжести в Кайенне была ниже. [45] [46] В 1687 году Исаак Ньютон в «Принципах математики» показал, что это произошло потому, что Земля не была настоящей сферой, а слегка сплюснутой (сплюснутой на полюсах) из-за воздействия центробежной силы из-за ее вращения, заставляющей гравитацию увеличиваться с широтой . [47] Портативные маятники стали брать с собой в путешествия к далеким землям в качестве прецизионных гравиметров для измерения ускорения силы тяжести в различных точках Земли, что в конечном итоге привело к созданию точных моделей формы Земли . [48]
Гюйгенса : Колебательные часы . 1673
В 1673 году, через 17 лет после изобретения часов с маятником, Христиан Гюйгенс опубликовал свою теорию маятника « Horologium Oscillatorium sive de motu pendulorum» . [49] [50] Около 1636 года Марин Мерсенн и Рене Декарт обнаружили, что маятник не совсем изохронен; его период несколько увеличивался вместе с его амплитудой. [51] Гюйгенс проанализировал эту проблему, определив, по какой кривой должен следовать объект, чтобы под действием силы тяжести спуститься в одну и ту же точку за один и тот же интервал времени, независимо от начальной точки; так называемая таутохронная кривая . С помощью сложного метода, который был одним из первых методов исчисления , он показал, что эта кривая представляет собой циклоиду , а не дугу окружности маятника. [52] подтверждая, что маятник не был изохронным, а наблюдение изохронности Галилеем было точным только для небольших колебаний. [53] Гюйгенс также решил задачу о том, как вычислить период маятника произвольной формы (называемого составным маятником ), обнаружив центр колебаний и его взаимозаменяемость с точкой поворота. [54]
Существующий механизм часов, а именно верхний спусковой механизм , заставлял маятники раскачиваться по очень широким дугам, около 100°. [55] Гюйгенс показал, что это было источником неточности, вызывающей изменение периода в зависимости от изменений амплитуды, вызванных небольшими неизбежными изменениями в движущей силе часов. [56] Чтобы сделать его период изохронным, Гюйгенс установил металлические направляющие циклоидальной формы рядом с осями своих часов, которые ограничивали подвесной шнур и заставляли маятник следовать по циклоидной дуге (см. Циклоидальный маятник ). [57] Это решение оказалось не таким практичным, как простое ограничение качания маятника небольшими углами в несколько градусов. Осознание того, что лишь небольшие колебания были изохронными, привело к созданию около 1670 года якорного спуска , который уменьшил поворот маятника в часах до 4–6 °. [55] [58] Это стало стандартным спусковым механизмом, используемым в маятниковых часах.
: Маятники с температурной компенсацией 1721

В XVIII и XIX веках роль маятниковых часов как самого точного хронометриста стимулировала множество практических исследований по совершенствованию маятников. Было обнаружено, что основным источником ошибок было то, что стержень маятника расширялся и сжимался при изменении температуры окружающей среды, изменяя период качания. [8] [59] Проблема была решена с изобретением маятников с температурной компенсацией, ртутного маятника в 1721 году. [60] и маятник-решетка в 1726 году, что уменьшило погрешность точных маятниковых часов до нескольких секунд в неделю. [57]
Точность гравитационных измерений, производимых маятниками, была ограничена трудностью определения положения их центра колебаний . В 1673 году Гюйгенс обнаружил, что период маятника, подвешенного за центр его колебаний, совпадает с периодом, когда он подвешен за ось. [17] а расстояние между двумя точками было равно длине простого гравитационного маятника того же периода. [14] В 1818 году британский капитан Генри Катер изобрел обратимый маятник Катера. [61] который использовал этот принцип, сделав возможным очень точные измерения гравитации. В течение следующего столетия обратимый маятник был стандартным методом измерения абсолютного гравитационного ускорения.
: Фуко маятник 1851
В 1851 году Жан Бернар Леон Фуко показал, что плоскость колебаний маятника, например гироскопа , имеет тенденцию оставаться постоянной независимо от движения оси вращения, и что это можно использовать для демонстрации вращения Земли . Он подвесил свободно качающийся в двух измерениях маятник (позже названный маятником Фуко ) на куполе Пантеона в Париже. Длина шнура составляла 67 м (220 футов). После того, как маятник был приведен в движение, было замечено, что плоскость его качания прецессировала или вращалась на 360° по часовой стрелке примерно за 32 часа. [62] Это была первая демонстрация вращения Земли, не зависящая от небесных наблюдений. [63] и вспыхнула «маятниковая мания», поскольку маятники Фуко были выставлены во многих городах и привлекли большие толпы людей. [64] [65]
использования Снижение 1930 :
Около 1900 года материалы с низким тепловым расширением начали использоваться для изготовления стержней маятника в часах высочайшей точности и других инструментах: сначала инвар , сплав никелевой стали, а затем плавленый кварц , что сделало температурную компенсацию тривиальной. [66] Прецизионные маятники размещались в резервуарах низкого давления, которые поддерживали постоянное давление воздуха, чтобы предотвратить изменения периода из-за изменения плавучести маятника из-за изменения атмосферного давления . [66] Лучшие маятниковые часы достигали точности около секунды в год. [67] [68]
Точность измерения времени маятника была превзойдена кварцевым генератором , изобретенным в 1921 году, а кварцевые часы , изобретенные в 1927 году, заменили маятниковые часы как лучшие в мире хронометры. [2] Маятниковые часы использовались в качестве эталонов времени до Второй мировой войны, хотя Французская служба времени продолжала использовать их в своем официальном ансамбле эталонов времени до 1954 года. [69] Маятниковые гравиметры были заменены гравиметрами «свободного падения» в 1950-х годах. [70] но маятниковые инструменты продолжали использоваться и в 1970-е годы.
Использование для измерения времени [ править ]
На протяжении 300 лет, с момента своего открытия около 1582 года до разработки кварцевых часов в 1930-х годах, маятник был мировым стандартом точного измерения времени. [2] [71] Помимо часовых маятников, свободно качающиеся секундные маятники в качестве точных таймеров в научных экспериментах в 17-18 веках широко использовались . Маятники требуют большой механической стабильности: изменение длины всего на 0,02% (0,2 мм в маятнике старинных часов) приведет к ошибке в минуту в неделю. [72]
Часовые маятники [ править ]
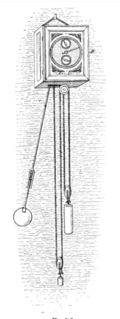
Маятники в часах (см. пример справа) обычно состоят из гири или груза (б), подвешенного на деревянном или металлическом стержне (а) . [8] [73] Чтобы уменьшить сопротивление воздуха (которое является причиной большей части потерь энергии в точных часах) [74] Боб традиционно представляет собой гладкий диск с поперечным сечением в форме линзы, хотя в старинных часах он часто имел резьбу или украшения, характерные для типа часов. В качественных часах боб делается настолько тяжелым, насколько его может выдержать подвеска и двигаться, поскольку это улучшает регулирование часов (см. «Точность» ниже). Обычный вес секундного маятникового бобса составляет 15 фунтов (6,8 кг). [75] Вместо того, чтобы подвешиваться на оси , маятники часов обычно поддерживаются короткой прямой пружиной (d) из гибкой металлической ленты. Это позволяет избежать трения и «люфта», вызванного шарниром, а небольшая изгибающая сила пружины просто увеличивает восстанавливающую силу маятника . В часах высочайшей точности стержни лезвий-ножей опираются на агатовые пластины. Импульсы для поддержания раскачивания маятника обеспечиваются рукой, висящей за маятником называемой костылем , (e) , которая заканчивается вилкой ( зубцы f), которой охватывают стержень маятника. Костыль перемещается вперед и назад с помощью спускового механизма часов (g,h) .
Каждый раз, когда маятник проходит через свое центральное положение, он освобождает один зуб спускового колеса (g) . часов Сила ходовой пружины часов или движущего груза, свисающего со шкива, передаваемая через зубчатую передачу , заставляет колесо вращаться, и зубец прижимается к одному из поддонов (h) , давая маятнику короткий толчок. Колеса часов, прикрепленные к спусковому колесу, перемещаются вперед на фиксированную величину при каждом повороте маятника, продвигая стрелки часов с постоянной скоростью.
Маятник всегда имеет средства регулировки периода, обычно с помощью регулировочной гайки (с) под качанием, которая перемещает его вверх или вниз на стержне. [8] [76] Перемещение качания вверх уменьшает длину маятника, заставляя маятник качаться быстрее, а часы ускоряют ход. Некоторые точные часы имеют небольшой вспомогательный регулировочный грузик на резьбовом валу на бобе, позволяющий осуществлять более точную регулировку. В некоторых башенных и прецизионных часах используется поднос, прикрепленный рядом с серединой стержня маятника, к которому можно добавлять или снимать небольшие грузики. Это эффективно смещает центр колебаний и позволяет регулировать скорость, не останавливая часы. [77] [78]
Маятник необходимо подвешивать на жесткой опоре. [8] [79] Во время работы любая упругость допускает малейшие незаметные покачивания опоры, что нарушает ход часов и приводит к ошибке. Маятниковые часы следует прочно прикрепить к прочной стене.
Наиболее распространенной длиной маятника в качественных часах, которая всегда используется в напольных часах , является секундный маятник , длиной около 1 метра (39 дюймов). В каминных часах используются полусекундные маятники длиной 25 см (9,8 дюйма) или короче. Лишь в нескольких больших башенных часах используются более длинные маятники: 1,5-секундный маятник длиной 2,25 м (7,4 фута) или иногда двухсекундный маятник длиной 4 м (13 футов). [8] [80] который используется в Биг Бене . [81]
Температурная компенсация [ править ]

Самым большим источником ошибок в ранних маятниках были небольшие изменения длины из-за теплового расширения и сжатия стержня маятника при изменении температуры окружающей среды. [82] Это было обнаружено, когда люди заметили, что маятниковые часы летом идут медленнее, на целую минуту в неделю. [59] [83] (одним из первых был Годфруа Венделен , о чем сообщил Гюйгенс в 1658 году). [84] Тепловое расширение стержней маятника было впервые изучено Жаном Пикаром в 1669 году. [85] [86] Маятник со стальным стержнем будет расширяться примерно на 11,3 частей на миллион (ppm) с каждым градусом Цельсия, в результате чего он будет терять около 0,27 секунды в день на каждый градус Цельсия повышения температуры или 9 секунд в день при повышении температуры на 33 °C. (59 °F) изменить. Деревянные стержни расширяются меньше, теряя всего около 6 секунд в день при изменении температуры на 33 ° C (59 ° F), поэтому в качественных часах часто использовались деревянные стержни маятника. Древесину пришлось покрыть лаком, чтобы предотвратить попадание водяного пара, ведь на длину влияла и перепады влажности.
Маятник Меркурия [ править ]
Первым устройством, компенсирующим эту ошибку, стал ртутный маятник, изобретенный Джорджем Грэмом. [60] в 1721 году. [8] [83] Жидкая металлическая ртуть увеличивается в объеме при повышении температуры. В ртутном маятнике груз маятника (качалка) представляет собой контейнер с ртутью. С повышением температуры стержень маятника удлиняется, но ртуть также расширяется, и уровень ее поверхности в сосуде несколько повышается, перемещая ее центр масс ближе к оси маятника. При использовании правильной высоты ртути в контейнере эти два эффекта будут компенсироваться, оставляя центр масс маятника и его период неизменными в зависимости от температуры. Его основным недостатком было то, что при изменении температуры стержень быстро достигал новой температуры, но массе ртути могло потребоваться день или два, чтобы достичь новой температуры, что приводило к отклонению скорости в течение этого времени. [87] Для улучшения теплопроводности часто использовались несколько тонких металлических контейнеров. Маятники Меркурия были стандартом, используемым в прецизионных часах с регулятором в 20 веке. [88]
Маятник Gridiron [ править ]
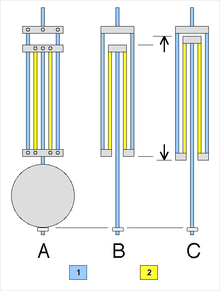
- внешняя схема
- нормальная температура
- более высокая температура
Наиболее широко используемым компенсированным маятником был маятник с решеткой , изобретенный в 1726 году Джоном Харрисоном . [8] [83] [87] Он состоит из чередующихся стержней из двух разных металлов: одного с более низким тепловым расширением ( КТР ) из стали , а другого - с более высоким тепловым расширением ( цинка или латуни) . Стержни соединены рамкой, как показано на рисунке справа, так что увеличение длины цинковых стержней подталкивает боб вверх, укорачивая маятник. При повышении температуры стальные стержни с низким расширением удлиняют маятник, а цинковые стержни с высоким расширением — короче. При изготовлении стержней правильной длины большее расширение цинка компенсирует расширение стальных стержней, которые имеют большую общую длину, и маятник остается одинаковой длины при изменении температуры.
Маятники из цинково-стальной решетки состоят из 5 стержней, но тепловое расширение латуни ближе к стали, поэтому для латунно-стальных решеток обычно требуется 9 стержней. Маятники с решеткой приспосабливаются к изменениям температуры быстрее, чем ртутные маятники, но ученые обнаружили, что трение стержней, скользящих в отверстиях в раме, заставляет маятники с решеткой регулироваться серией крошечных прыжков. [87] В высокоточных часах это приводило к внезапному изменению хода часов при каждом скачке. Позже было установлено, что цинк подвержен ползучести . По этим причинам ртутные маятники использовались в часах высочайшей точности, а в часах с качественным регулятором использовались решётки.
Маятники Gridiron настолько стали ассоциироваться с хорошим качеством, что по сей день многие обычные маятники для часов имеют декоративные «фальшивые» решётки, которые на самом деле не имеют никакой функции температурной компенсации.
Инвар и плавленый кварц [ править ]
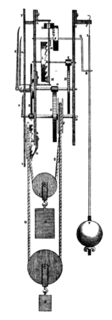
Примерно в 1900 году были разработаны материалы с низким тепловым расширением, которые можно было использовать в качестве маятниковых стержней, чтобы сделать ненужной сложную температурную компенсацию. [8] [83] Они использовались лишь в некоторых часах высочайшей точности, прежде чем маятник устарел как стандарт времени. В 1896 году Шарль Эдуард Гийом изобрел никелевой стали сплав инвар . Его КТР составляет около 0,9 частей на миллион /°C ( 0,5 частей на миллион/°F ), что приводит к ошибкам температуры маятника выше 22 °C (71 °F) всего на 1,3 секунды в день, и эта остаточная ошибка может быть скомпенсирована до нуля с помощью несколько сантиметров алюминия под качанием маятника [2] [87] (это можно увидеть на изображении часов Riefler выше). Инваровые маятники впервые были использованы в 1898 году в часах-регуляторах Рифлера. [89] который достиг точности 15 миллисекунд в день. Пружины подвески Элинвар пружины были использованы для устранения температурного изменения восстанавливающей силы на маятнике. Позже стал использоваться плавленый кварц с еще меньшим КТР. Эти материалы являются выбором для современных маятников высокой точности. [90]
Атмосферное давление [ править ]
Влияние окружающего воздуха на движущийся маятник сложное и требует точного расчета механики жидкости , но для большинства целей его влияние на период можно объяснить тремя эффектами: [66] [91]
- По принципу Архимеда эффективный вес качания масса уменьшается за счет плавучести воздуха, который он вытесняет, в то время как ( инерция ) остается прежней, что уменьшает ускорение маятника во время его качания и увеличивает период. Это зависит от давления воздуха и плотности маятника, но не от его формы.
- При качании маятник несет с собой некоторое количество воздуха, и масса этого воздуха увеличивает инерцию маятника, снова уменьшая ускорение и увеличивая период. Это зависит как от его плотности, так и от формы.
- Вязкое сопротивление воздуха замедляет скорость маятника. Это оказывает незначительное влияние на период, но рассеивает энергию, уменьшая амплитуду. маятника Это уменьшает добротность , требуя более сильной движущей силы от механизма часов, чтобы поддерживать его движение, что приводит к увеличению нарушения периода.
Увеличение барометрического давления немного увеличивает период маятника из-за первых двух эффектов, примерно на 0,11 секунды в день на килопаскаль (0,37 секунды в день на дюйм ртутного столба ; 0,015 секунды в день на торр ). [66] Исследователям, использующим маятники для измерения ускорения силы тяжести, пришлось корректировать период давления воздуха на высоте измерения, вычисляя эквивалентный период маятника, раскачивающегося в вакууме. Впервые маятниковые часы были использованы в резервуаре с постоянным давлением Фридрихом Тиде в 1865 году в Берлинской обсерватории . [92] [93] а к 1900 году часы высочайшей точности были установлены в резервуарах, в которых поддерживалось постоянное давление, чтобы исключить изменения атмосферного давления. Альтернативно, в некоторых случаях этот эффект компенсировался небольшим механизмом барометра-анероида, прикрепленным к маятнику.
Гравитация [ править ]
На маятники влияют изменения гравитационного ускорения, которое варьируется на целых 0,5% в разных местах Земли, поэтому точные маятниковые часы необходимо перекалибровывать после перемещения. Даже перемещение маятниковых часов на вершину высокого здания может привести к тому, что они потеряют измеримое время из-за уменьшения гравитации.
маятников хронометристов Точность как
Элементы измерения времени во всех часах, к которым относятся маятники, балансовые колеса , кристаллы кварца , используемые в кварцевых часах , и даже вибрирующие атомы в атомных часах , в физике называются гармоническими осцилляторами . Причина, по которой гармонические генераторы используются в часах, заключается в том, что они вибрируют или колеблются с определенной резонансной частотой или периодом и сопротивляются колебаниям с другими скоростями. Однако резонансная частота не является бесконечно «острой». Вокруг резонансной частоты существует узкая естественная полоса частот (или периодов), называемая шириной резонанса или полосой пропускания , в которой будет колебаться гармонический генератор. [94] [95] В часах фактическая частота маятника может случайным образом изменяться в пределах этой ширины резонанса в ответ на возмущения, но на частотах за пределами этого диапазона часы вообще не будут работать. Ширина резонанса определяется затуханием — потерей энергии на трение при каждом качании маятника.
Q- фактор [ править ]

Мерой устойчивости гармонического генератора к возмущениям его периода колебаний является безразмерный параметр, называемый добротностью, равный резонансной частоте, деленной на ширину резонанса . [95] [96] Чем выше Q , тем меньше ширина резонанса и тем более постоянна частота или период генератора для данного возмущения. [97] Обратная величина Q примерно пропорциональна предельной точности, достижимой с помощью гармонического генератора в качестве эталона времени. [98]
Q связана с тем , сколько времени требуется, чтобы колебания осциллятора затухли. Добротность маятника можно измерить, подсчитав количество колебаний , необходимое для того, чтобы амплитуда качания маятника затухала до 1/ e = 36,8% от его первоначального колебания, и умножив его на 'π .
часов, В часах маятник должен получать толчки от движения чтобы поддерживать его колебание, чтобы восполнить энергию, которую маятник теряет из-за трения. Эти толчки, применяемые механизмом, называемым спусковым механизмом , являются основным источником нарушения движения маятника. Q кратной энергии, запасенной в маятнике, разделенной на энергию , равен 2 π- теряемую на трение в течение каждого периода колебаний, что равно энергии, добавляемой спусковым механизмом за каждый период. Можно видеть, что чем меньшая часть энергии маятника теряется на трение, тем меньше энергии нужно добавить, тем меньше возмущение от спускового механизма, тем более «независим» маятник от часового механизма, и более постоянным является его период. Q : маятника определяется выражением
ω фиксируется периодом маятника, а M ограничивается грузоподъемностью и жесткостью подвески. Таким образом, добротность маятников часов увеличивается за счет минимизации потерь на трение (Γ). Прецизионные маятники подвешены на шарнирах с низким коэффициентом трения, состоящих из «ножевых» кромок треугольной формы, опирающихся на агатовые пластины. Около 99% потерь энергии в свободно качающемся маятнике происходит из-за трения воздуха, поэтому установка маятника в вакуумном резервуаре может увеличить Q и, следовательно, точность в 100 раз. [99]
Добротность маятников колеблется от нескольких тысяч у обычных часов до нескольких сотен тысяч у маятников прецизионных регуляторов, качающихся в вакууме. [100] Качественные домашние маятниковые часы могут иметь добротность 10 000 и точность 10 секунд в месяц. Самыми точными коммерчески выпускаемыми маятниковыми часами были часы со свободным маятником Shortt-Synchronome , изобретенные в 1921 году. [2] [67] [101] [102] [103] Его главный маятник из инвара , качающийся в вакуумном резервуаре, имел добротность 110 000. [100] и частота ошибок около секунды в год. [67]
Их вопрос из 10 3 –10 5 Это одна из причин, почему маятники являются более точными хронометристами чем балансовые колеса , в часах с добротностью около 100–300, но менее точными, чем кристаллы кварца в кварцевых часах с добротностью 10. 5 –10 6 . [2] [100]
Спуск [ править ]
Маятники (в отличие, например, от кристаллов кварца) имеют достаточно низкую добротность , поэтому возмущения, вызываемые импульсами, заставляющими их двигаться, обычно являются ограничивающим фактором для точности их измерения времени. Следовательно, конструкция спускового механизма , механизма, обеспечивающего эти импульсы, оказывает большое влияние на точность маятника часов. Если бы импульсы, передаваемые маятнику при каждом качании спуска, были бы совершенно одинаковыми, реакция маятника была бы одинаковой, а его период был бы постоянным. Однако это недостижимо; неизбежные случайные колебания силы из-за трения паллет часов, изменений смазки и изменений крутящего момента, обеспечиваемого источником питания часов по мере его истощения, означают, что сила импульса, приложенного спусковым механизмом, меняется.
Если эти изменения силы спуска вызывают изменения ширины (амплитуды) качания маятника, это вызовет соответствующие небольшие изменения периода, поскольку (как обсуждалось выше) маятник с конечным колебанием не совсем изохронен. Таким образом, цель традиционной конструкции спускового механизма состоит в том, чтобы приложить силу с правильным профилем и в правильной точке цикла маятника, чтобы изменения силы не влияли на амплитуду маятника. Это называется изохронным спуском .
Состояние Эйри [ править ]
Часовщики на протяжении веков знали, что возмущающее воздействие движущей силы спускового механизма на период маятника будет минимальным, если оно будет дано в виде короткого импульса, когда маятник проходит через свое нижнее положение равновесия . [2] Если импульс возникает до того, как маятник достигнет дна, во время движения вниз, это приведет к сокращению естественного периода маятника, поэтому увеличение движущей силы уменьшит период. Если импульс возникает после того, как маятник достигнет дна, во время подъема, он удлинит период, поэтому увеличение движущей силы увеличит период маятника. в 1826 году британский астроном Джордж Эйри Это доказал ; в частности, он доказал, что если маятник приводится в движение импульсом, симметричным относительно его нижнего положения равновесия, на период маятника не будут влиять изменения движущей силы. [104] Наиболее точные спусковые механизмы, такие как «мертвый» спуск , примерно удовлетворяют этому условию. [105]
Измерение силы тяжести [ править ]
Наличие ускорения свободного падения g в уравнении периодичности (1) для маятника означает, что местное ускорение свободного падения Земли можно вычислить по периоду маятника. Таким образом, маятник можно использовать в качестве гравиметра для измерения местной силы тяжести , которая варьируется более чем на 0,5% по поверхности Земли. [106] [Примечание 2] Маятник в часах расстраивается из-за толчков, которые он получает от часового механизма, поэтому использовались свободно качающиеся маятники, которые были стандартными инструментами гравиметрии до 1930-х годов.
Разница между маятниками-часами и маятниками-гравиметрами заключается в том, что для измерения силы тяжести необходимо измерить длину маятника, а также его период. Период свободного качания маятников можно было определить с большой точностью, сравнив их колебания с точными часами, которые были настроены так, чтобы показывать точное время по прохождению звезд над головой. В первых измерениях перед маятником часов подвешивался груз на шнуре, и его длина регулировалась до тех пор, пока два маятника не качались точно синхронно. Затем измерили длину шнура. Зная длину и период, g можно рассчитать по уравнению (1).
Секундный маятник [ править ]
Секундный маятник , маятник с периодом в две секунды, так что каждое колебание занимает одну секунду, широко использовался для измерения гравитации, потому что его период можно было легко измерить, сравнивая его с часами с точным регулятором , у всех которых были секундные маятники. К концу 17 века длина секундного маятника стала стандартной мерой силы гравитационного ускорения в определенном месте. К 1700 году его длина была измерена с точностью до миллиметра в нескольких городах Европы. Для секундного маятника g пропорционально его длине:
Ранние наблюдения [ править ]
- 1620 : Британский учёный Фрэнсис Бэкон был одним из первых, кто предложил использовать маятник для измерения гравитации. Он предложил подняться на гору и посмотреть, меняется ли сила тяжести с высотой. [107]
- 1644 : Еще до появления часов с маятником французский священник Марин Мерсенн впервые определил, что длина секундного маятника составляет 39,1 дюйма (990 мм), сравнив колебание маятника со временем, за которое груз упал на измеренное расстояние. Он также был первым, кто обнаружил зависимость периода от амплитуды колебаний.
- 1669 : Жан Пикард определил длину секундного маятника в Париже, используя медный шарик диаметром 1 дюйм (25 мм), подвешенный на волокне алоэ, и получил 39,09 дюйма (993 мм). [108] Он также провел первые эксперименты по тепловому расширению и сжатию стержней маятника при изменении температуры.
- 1672 : Первое наблюдение того, что сила тяжести различается в разных точках Земли, было сделано в 1672 году Жаном Рише , который привез маятниковые часы в Кайенну , Французская Гвиана , и обнаружил, что они теряют 2 + 1 / 2 минуты в день; его секундный маятник пришлось укоротить на 1 + 1 ⁄ На линии (2,6 мм) короче, чем в Париже, для точного времени. [109] [110] В 1687 году Исаак Ньютон в «Принципах математики» показал, что это произошло потому, что Земля имела слегка сплюснутую форму (сплюснутую у полюсов), вызванную центробежной силой ее вращения. В более высоких широтах поверхность была ближе к центру Земли, поэтому сила тяжести увеличивалась с широтой. [110] С этого времени маятники стали возить в дальние страны для измерения гравитации и составляли таблицы длины секундного маятника в разных местах Земли. В 1743 году Алексис Клод Клеро создал первую гидростатическую модель Земли — теорему Клеро . [108] что позволило рассчитать эллиптичность Земли на основе гравитационных измерений. Затем последовали все более точные модели формы Земли.
- 1687 : Ньютон экспериментировал с маятниками (описанными в «Принципах» ) и обнаружил, что маятники одинаковой длины с качаниями, сделанными из разных материалов, имеют одинаковый период, доказав, что сила гравитации, действующая на разные вещества, точно пропорциональна их массе (инерции). Этот принцип, получивший название принципа эквивалентности , подтвержденный с большей точностью в более поздних экспериментах, стал основой, на которой Альберт Эйнштейн основал свою общую теорию относительности .

- 1737 : Французский математик Пьер Буге провел сложную серию маятниковых наблюдений в Андах , Перу. [111] Он использовал медный маятник в форме двузаостренного конуса, подвешенный на нити; боб можно было перевернуть, чтобы устранить эффекты неравномерной плотности. Он рассчитал длину до центра колебаний нити и боба вместе, вместо того, чтобы использовать центр боба. Он сделал поправку на тепловое расширение измерительного стержня и барометрическое давление, получив результаты для маятника, раскачивающегося в вакууме. Буге раскачивал один и тот же маятник на трех разных высотах: от уровня моря до вершины высокогорного перуанского альтиплано . Гравитация должна падать обратно пропорционально квадрату расстояния от центра Земли. Бугер обнаружил, что он падал медленнее, и правильно объяснил «дополнительную» гравитацию гравитационным полем огромного Перуанского плато. По плотности образцов горных пород он рассчитал примерное влияние альтиплано на маятник и, сравнив это с гравитацией Земли, смог сделать первую приблизительную оценку плотности Земли. .
- 1747 : Даниэль Бернулли показал, как исправить удлинение периода из-за конечного угла поворота θ 0 , используя поправку первого порядка θ 0. 2 /16, что дает период маятника с чрезвычайно малым колебанием. [111]
- 1792 : Чтобы определить эталон длины маятника для использования в новой метрической системе , в 1792 году Жан-Шарль де Борда и Жан-Доминик Кассини произвели точное измерение секундного маятника в Париже. Они использовали 1 + 1 ⁄ 2 дюйма (14 мм) [ нужны разъяснения ] платиновый шар, подвешенный на железной проволоке длиной 12 футов (3,7 м). Их главным нововведением был метод, названный « методом совпадений », который позволял с большой точностью сравнивать период маятников. (Бугер также использовал этот метод). Был рассчитан временной интервал Δt между повторяющимися моментами, когда два маятника качались синхронно. разницу между периодами маятников Т 1 и Т 2 : Отсюда можно вычислить
- 1821 : Франческо Карлини провел маятниковые наблюдения на вершине горы Сени в Италии, на основе которых, используя методы, аналогичные методам Буге, он рассчитал плотность Земли. [112] Он сравнил свои измерения с оценкой силы тяжести в том месте, где он находился, предполагая, что горы там нет, рассчитанной на основе предыдущих измерений маятника на уровне моря. Его измерения показали «избыточную» гравитацию, которую он объяснил влиянием горы. Смоделировав гору как сегмент сферы диаметром 11 миль (18 км) и высотой 1 милю (1,6 км), он по образцам горных пород рассчитал ее гравитационное поле и оценил плотность Земли в 4,39 раза больше плотности воды. Более поздние перерасчеты, проведенные другими, дали значения 4,77 и 4,95, что иллюстрирует неопределенность этих географических методов.
Kater's pendulum [ edit ]
 |  |

была ограничена трудностью измерения длины маятника L. Точность первых измерений силы тяжести, описанных выше , L была длиной идеализированного простого гравитационного маятника (описанного вверху), вся масса которого сосредоточена в точке на конце шнура. В 1673 году Гюйгенс показал, что период маятника с жестким стержнем (названного составным маятником ) равен периоду простого маятника с длиной, равной расстоянию между точкой поворота и точкой, называемой центром колебаний , расположенной под центр тяжести , который зависит от распределения массы вдоль маятника. Но точного способа определения центра колебаний реального маятника не существовало.
Чтобы обойти эту проблему, первые исследователи, описанные выше, максимально приблизили идеальный простой маятник, используя металлическую сферу, подвешенную на световом проводе или шнуре. Если проволока была достаточно легкой, центр колебаний находился близко к центру тяжести шара, в его геометрическом центре. Этот маятник типа «шарик и проволока» не был очень точным, потому что он не качался как твердое тело, а эластичность проволоки приводила к незначительному изменению его длины при качании маятника.
Однако Гюйгенс также доказал, что в любом маятнике точка поворота и центр колебаний взаимозаменяемы. [17] То есть, если маятник перевернуть и повесить за его центр колебаний, он будет иметь тот же период, что и в предыдущем положении, а старая точка поворота будет новым центром колебаний.
Британский физик и армейский капитан Генри Катер в 1817 году понял, что принцип Гюйгенса можно использовать для определения длины простого маятника с тем же периодом, что и у настоящего маятника. [61] Если маятник был построен со второй регулируемой точкой поворота рядом с нижней частью, чтобы его можно было подвешивать вверх ногами, а второй шарнир регулировался до тех пор, пока периоды подвешивания на обоих шарнирах не стали одинаковыми, второй шарнир находился бы в центре колебаний. , а расстояние между двумя точками опоры будет равно длине L простого маятника с тем же периодом.
Катер построил обратимый маятник ( см. рисунок ), состоящий из латунного стержня с двумя противоположными шарнирами, сделанными из коротких треугольных «ножевых» лезвий (а) на обоих концах. Его можно было поворачивать на любой оси, при этом лезвия ножа опирались на агатовые пластины. Вместо того, чтобы сделать один шарнир регулируемым, он прикрепил шарниры на расстоянии метра друг от друга и вместо этого регулировал периоды с помощью подвижного груза на стержне маятника (b,c) . Во время работы маятник подвешивают перед точными часами и отсчитывают время, затем переворачивают и снова отсчитывают период. Вес регулируется регулировочным винтом до тех пор, пока периоды не станут равными. гравитационное ускорение g Тогда помещение этого периода и расстояния между точками опоры в уравнение (1) дает очень точное .
Катер рассчитал время качания маятника, используя « метод совпадений », и измерил расстояние между двумя точками опоры с помощью микрометра. После внесения поправок на конечную амплитуду качания, плавучесть качания, барометрическое давление, высоту и температуру он получил значение 39,13929 дюймов для секундного маятника в Лондоне, в вакууме, на уровне моря, при температуре 62 ° F. . Наибольшее отклонение от среднего значения из его 12 наблюдений составило 0,00028 дюйма. [113] что соответствует точности измерения силы тяжести 7×10. −6 (7 мГал или 70 мкм/с 2 ). Измерение Катера использовалось в качестве официального стандарта длины Великобритании (см. ниже ) с 1824 по 1855 год.
Реверсивные маятники (известные технически как «конвертируемые» маятники), использующие принцип Катера, использовались для измерений абсолютной силы тяжести в 1930-х годах.
маятниковые поздние Более гравиметры
Повышенная точность, ставшая возможной благодаря маятнику Катера, помогла сделать гравиметрию стандартной частью геодезии . Поскольку точное местоположение (широта и долгота) «станции», где производились измерения силы тяжести, было необходимо, измерения силы тяжести стали частью геодезических работ , а маятники использовались в великих геодезических исследованиях 18-го века, в частности в Великой тригонометрической съемке 18 -го века. Индия.

- Неизменные маятники: Катер представил идею измерений относительной силы тяжести в дополнение к абсолютным измерениям, выполняемым маятником Катера. [114] Сравнение гравитации в двух разных точках было более простым процессом, чем абсолютное ее измерение методом Катера. Все, что было необходимо, — это замерить период обычного (одноповоротного) маятника в первой точке, затем перевезти маятник в другую точку и засечь там его период. Поскольку длина маятника была постоянной, из (1) соотношение гравитационных ускорений было равно обратному отношению квадратов периодов, и никаких точных измерений длины не требовалось. Таким образом, как только гравитация была абсолютно измерена на какой-то центральной станции с помощью Катера или другого точного метода, гравитацию в других точках можно было определить, раскачивая маятники на центральной станции, а затем перенося их в другое место и рассчитывая время их качания там. Катер создал набор «неизменных» маятников только с одной ножевой осью, которые были перевезены во многие страны после того, как их впервые раскачали на центральной станции обсерватории Кью в Великобритании.
- Эксперименты Эйри с угольной ямой . Начиная с 1826 года, используя методы, аналогичные методу Бугера, британский астроном Джордж Эйри попытался определить плотность Земли с помощью маятниковых гравитационных измерений наверху и внизу угольной шахты. [115] [116] Гравитационная сила под поверхностью Земли с глубиной уменьшается, а не увеличивается, поскольку по закону Гаусса масса сферической оболочки коры над точкой недр не вносит вклад в силу тяжести. Эксперимент 1826 года был прерван из-за затопления шахты, но в 1854 году он провел улучшенный эксперимент на угольной шахте Хартон, используя секундные маятники, качающиеся на агатовых пластинах, синхронизированные точными хронометрами, синхронизированными электрической цепью. Он обнаружил, что нижний маятник работал медленнее на 2,24 секунды в день. Это означало, что гравитационное ускорение на дне шахты, на высоте 1250 футов под поверхностью, было на 1/14 000 меньше, чем должно было быть по закону обратных квадратов; то есть притяжение сферической оболочки составляло 1/14 000 притяжения Земли. По образцам поверхностных пород он оценил массу сферической оболочки коры и на основании этого пришел к выводу, что плотность Земли в 6,565 раз превышает плотность воды. Фон Штернек попытался повторить эксперимент в 1882 году, но получил противоречивые результаты.

- Маятник Репсольда-Бесселя: многократное раскачивание маятника Катера и корректировка весов до тех пор, пока периоды не станут равными, требовали много времени и были подвержены ошибкам. Фридрих Бессель в 1835 году показал, что в этом нет необходимости. [117] Пока периоды были близки друг к другу, силу тяжести можно было рассчитать по двум периодам и центру тяжести маятника. [118] Таким образом, реверсивный маятник не нужно было регулировать, это могла быть просто штанга с двумя шарнирами. Бессель также показал, что если маятник сделать симметричным по форме относительно своего центра, но иметь внутренний вес на одном конце, ошибки, связанные с сопротивлением воздуха, будут компенсированы. Кроме того, еще одна ошибка, связанная с конечным диаметром кромок ножа, может быть устранена, если их менять местами между измерениями. Бессель не сконструировал такой маятник, но в 1864 году Адольф Репсольд по контракту Швейцарской геодезической комиссии изготовил маятник по этому принципу. Маятник Репсольда имел длину около 56 см и период около 3/4 секунды . Он широко использовался европейскими геодезическими агентствами, а также вместе с маятником Катера в Обзоре Индии. Подобные маятники этого типа были разработаны Ч. Пирсом и К. Дефоржем.

- Гравиметры фон Штернека и Менденхолла: в 1887 году австро-венгерский ученый Роберт фон Штернек разработал небольшой маятник гравиметра, установленный в вакуумном резервуаре с регулируемой температурой, чтобы исключить влияние температуры и давления воздуха. В нем использовался «полсекундный маятник» с периодом около одной секунды и длиной около 25 см. Маятник был необратимым, поэтому прибор использовался для измерений относительной силы тяжести, но небольшой размер делал его небольшим и портативным. Период маятника определялся путем отражения изображения электрической искры , создаваемой точным хронометром, от зеркала, установленного наверху стержня маятника. Инструмент фон Штернека и аналогичный инструмент, разработанный Томасом К. Менденхоллом из Береговой и геодезической службы США в 1890 году, [119] широко использовались для исследований в 1920-е годы.
- Маятник Менденхолла фактически был более точным хронометристом, чем самые точные часы того времени, и как «лучшие в мире часы» он использовался Альбертом А. Майкельсоном в его измерениях скорости света в 1924 году на горе Вильсон, Калифорния. [119]
- Гравиметры с двойным маятником: начиная с 1875 года повышение точности маятниковых измерений выявило еще один источник ошибок в существующих инструментах: качание маятника вызывало небольшое покачивание штатива, используемого для поддержки переносных маятников, что вносило ошибку. В 1875 году Чарльз С. Пирс подсчитал, что измерения длины секундного маятника, выполненные с помощью инструмента Репсольда, требуют поправки на 0,2 мм из-за этой ошибки. [120] В 1880 году К. Дефорж использовал интерферометр Майкельсона для динамического измерения раскачивания стенда, а к стандартному аппарату Менденхолла были добавлены интерферометры для расчета поправок на раскачивание. [121] Метод предотвращения этой ошибки был впервые предложен в 1877 году Эрве Фаем и предложен Пирсом, Селлерье и Фуртвенглером: установить на одной опоре два одинаковых маятника, качающихся с одинаковой амплитудой и сдвинутыми по фазе на 180°. Противоположное движение маятников нейтрализует любые боковые силы, действующие на опору. Идея встретила сопротивление из-за ее сложности, но к началу 20-го века устройство фон Штернека и другие инструменты были модифицированы для одновременного качания нескольких маятников.

- Гравиметр Gulf : Одним из последних и наиболее точных маятниковых гравиметров был аппарат, разработанный в 1929 году компанией Gulf Research and Development Co. [122] [123] В нем использовались два маятника из плавленого кварца , каждый длиной 10,7 дюйма (270 мм) с периодом 0,89 секунды, качающиеся на шарнирах с ножевой кромкой из пирекса, сдвинутые по фазе на 180 °. Они были установлены в постоянно герметичной вакуумной камере с контролируемой температурой и влажностью. Случайные электростатические заряды на кварцевых маятниках необходимо было снять, подвергнув их воздействию радиоактивной соли перед использованием. Период определялся путем отражения светового луча от зеркала в верхней части маятника, записывался самописцем и сравнивался с прецизионным кварцевым генератором, откалиброванным по WWV радиосигналу времени . Этот прибор имел точность в пределах (0,3–0,5)×10. −7 (30–50 микрогал или 3–5 нм/с 2 ). [122] Его использовали в 1960-х годах.
Относительные маятниковые гравиметры были заменены более простым весенним гравиметром LaCoste с нулевой длиной, изобретенным в 1934 году Люсьеном Лакостом . [119] Абсолютные (обратимые) маятниковые гравиметры были заменены в 1950-х годах гравиметрами свободного падения, в которых груз падает в вакуумный резервуар, а его ускорение измеряется оптическим интерферометром . [70]
Стандарт длины [ править ]
Поскольку ускорение силы тяжести в данной точке Земли постоянно, период простого маятника в данном месте зависит только от его длины. Кроме того, гравитация лишь незначительно различается в разных местах. Практически с момента открытия маятника до начала 19 века это свойство побудило ученых предложить использовать маятник определенного периода в качестве эталона длины .
До XIX века страны основывали свои системы измерения длины на прототипах, первичных эталонах металлических стержней , таких как стандартный ярд в Великобритании, хранящийся в здании парламента, и стандартный туаз во Франции, хранящийся в Париже. На протяжении многих лет они были уязвимы для повреждений или разрушения, а из-за сложности сравнения прототипов одни и те же устройства часто имели разную длину в отдаленных городах, что создавало возможности для мошенничества. [124] В эпоху Просвещения ученые выступали за стандарт длины, основанный на каком-то свойстве природы, которое можно было определить путем измерения, создавая неразрушимый универсальный стандарт. Период маятников можно было очень точно измерить, синхронизируя их с часами, установленными по звездам. Стандарт маятника сводился к определению единицы длины силой гравитации Земли, по сути постоянной, и секунды, которая определялась скоростью вращения Земли , также постоянной. Идея заключалась в том, что любой человек в любой точке Земли мог воссоздать стандарт, построив маятник, который качался с определенным периодом, и измерив его длину.
Практически все предложения основывались на секундном маятнике , у которого каждое колебание (полупериода ) занимает одну секунду, что составляет около метра (39 дюймов) в длину, поскольку к концу 17 века он стал эталоном измерения силы тяжести (см. предыдущий раздел). К XVIII веку его длину измеряли с точностью до миллиметра в ряде городов Европы и мира.
Первоначальной привлекательностью стандарта длины маятника было то, что считалось (ранние ученые, такие как Гюйгенс и Рен), что гравитация постоянна над поверхностью Земли, поэтому данный маятник имел одинаковый период в любой точке Земли. [124] Таким образом, длину стандартного маятника можно было измерить в любом месте и не привязывать к какой-либо конкретной стране или региону; это был бы поистине демократический всемирный стандарт. Хотя в 1672 году Ричер обнаружил, что сила тяжести варьируется в разных точках земного шара, идея стандарта длины маятника оставалась популярной, поскольку было обнаружено, что сила тяжести меняется только в зависимости от широты . Гравитационное ускорение плавно увеличивается от экватора к полюсам из- за сплюснутой формы Земли, поэтому на любой заданной широте (линия восток-запад) гравитация была достаточно постоянной, чтобы длина секундного маятника была одинаковой в пределах возможностей измерения. XVIII века. Таким образом, единицу длины можно было определить на данной широте и измерить в любой точке этой широты. Например, популярный маятниковый стандарт, определенный на 45° северной широты, может быть измерен в некоторых частях Франции, Италии, Хорватии, Сербии, Румынии, России, Казахстана, Китая, Монголии, США и Канады. Кроме того, его можно было воссоздать в любом месте, где было точно измерено гравитационное ускорение.
К середине 19-го века все более точные маятниковые измерения Эдварда Сабина и Томаса Янга показали, что сила тяжести и, следовательно, длина любого маятникового стандарта заметно различаются в зависимости от местных геологических особенностей, таких как горы и плотные подземные породы. [125] Таким образом, стандарт длины маятника должен был быть определен в одной точке Земли и мог быть измерен только там. Это лишило концепцию большей привлекательности, и попытки принять маятниковые стандарты были оставлены.
Ранние предложения
Одним из первых, кто предложил определять длину с помощью маятника, был фламандский учёный Исаак Бекман. [126] который в 1631 году рекомендовал сделать секундный маятник «неизменной мерой для всех людей, во все времена и во всех местах». [127] Это предположил и Марин Мерсенн , который впервые измерил секундный маятник в 1644 году. Первое официальное предложение о стандарте маятника было сделано Британским королевским обществом в 1660 году, его отстаивали Христиан Гюйгенс и Оле Рёмер , основываясь на работе Мерсенна. [128] и Гюйгенс в «Horologium Oscillatorium» предложили «часовой фут», определяемый как 1/3 секунды маятника. Кристофер Рен был еще одним ранним сторонником. Идея маятникового эталона длины, должно быть, была знакома людям еще в 1663 году, потому что Сэмюэл Батлер высмеивает ее в «Худибрасе» : [129]
- На скамейке я с ними разберусь
- Что вибрация этого маятника
- Сделаем все портные дворы одним
- Единогласное мнение
В 1671 году Жан Пикард » предложил маятниковую «универсальную стопу» в своей влиятельной работе «Mesure de la Terre . [130] Габриэль Мутон около 1670 года предложил определять туаз либо по секундному маятнику, либо по минуте земного градуса. План создания полной системы единиц на основе маятника был предложен в 1675 году итальянским эрудитом Тито Ливио Бурратини. Во Франции в 1747 году географ Шарль Мари де ла Кондамин предложил определять длину с помощью секундного маятника на экваторе; поскольку в этом месте колебание маятника не будет искажаться вращением Земли. Джеймс Стюарт (1780 г.) и Джордж Скин Кейт также были сторонниками.
К концу 18-го века, когда многие страны реформировали свои системы измерения и веса , секундный маятник стал основным выбором для нового определения длины, за которое выступали выдающиеся ученые в нескольких крупных странах. В 1790 году тогдашний госсекретарь США Томас Джефферсон предложил Конгрессу всеобъемлющую десятичную «метрическую систему» США, основанную на секундном маятнике на 38 ° северной широты, средней широте Соединенных Штатов. [131] Никаких действий по этому предложению предпринято не было. В Великобритании ведущим сторонником маятника был политик Джон Риггс Миллер . [132] Когда в 1790 году его усилия по продвижению совместной британо-французско-американской метрической системы провалились, он предложил британскую систему, основанную на длине секундного маятника в Лондоне. Этот стандарт был принят в 1824 году (ниже).
Метр [ править ]
В дискуссиях, приведших к принятию во Франции метрической системы в 1791 году, ведущим кандидатом на определение новой единицы длины, метра , был секундный маятник на 45° северной широты. За это выступала группа во главе с французским политиком Талейраном и математиком Антуаном Николя Каритатом де Кондорсе . Это был один из трех окончательных вариантов, рассмотренных комитетом Французской академии наук . Однако 19 марта 1791 года комитет вместо этого решил основывать метр на длине меридиана, проходящего через Париж. Определение маятника было отвергнуто из-за его изменчивости в разных местах и потому, что оно определяло длину в единице времени. (Однако с 1983 года метр официально определялся как длина секунды и скорость света.) Возможная дополнительная причина заключается в том, что радикальная Французская академия не хотела основывать свою новую систему на секунде, традиционная и недесятичная единица из древнего режима .
Хотя это и не определяется маятником, окончательная длина, выбранная для метра, составляет 10 −7 от полюса до экватора дуги меридиана , была очень близка к длине секундного маятника (0,9937 м), с точностью до 0,63%. Хотя в то время не было указано никаких причин для этого конкретного выбора, вероятно, это было сделано для облегчения использования секундного маятника в качестве вторичного стандарта, как было предложено в официальном документе. Таким образом, стандартная единица длины современного мира, безусловно, исторически тесно связана с секундным маятником.
Великобритания и Дания [ править ]
Великобритания и Дания, по-видимому, являются единственными странами, которые (в течение короткого времени) основывали свои единицы длины на маятнике. В 1821 году датский дюйм был определен как 1/38 длины среднего солнечного секундного маятника на 45° широты на меридиане Скагена , на уровне моря, в вакууме. [133] [134] В 1824 году британский парламент принял Закон об имперских мерах и весах , реформу британской стандартной системы, в которой говорилось, что, если прототип стандартного ярда будет разрушен, он будет восстановлен путем определения дюйма так, чтобы длина маятника солнечных секунд в Лондоне На уровне моря , в вакууме, при температуре 62 °F было 39,1393 дюйма. [135] Это также стало стандартом США, поскольку в то время США использовали британские меры. Однако, когда верфь прототипа была потеряна во время пожара в здании парламента в 1834 году , оказалось невозможным точно воссоздать его на основе определения маятника, и в 1855 году Великобритания отменила стандарт маятника и вернулась к стандартам прототипа.
Другое использование [ править ]
Сейсмометры [ править ]
Маятник, у которого стержень расположен не вертикально, а почти горизонтально, использовался в первых сейсмометрах для измерения земных толчков. Боб маятника не движется при его креплении, а разница в движениях фиксируется на барабанной диаграмме.
Тюнинг Шулера [ править ]
Как впервые объяснил Максимилиан Шулер в статье 1923 года, маятник, период которого точно равен периоду обращения гипотетического спутника, вращающегося по орбите чуть выше поверхности Земли (около 84 минут), будет стремиться продолжать указывать на центр Земли, когда его поддержка внезапно смещается. Этот принцип, получивший название настройки Шулера , используется в инерциальных системах наведения кораблей и самолетов, работающих на поверхности Земли. Физический маятник не используется, но система управления , обеспечивающая устойчивость инерционной платформы , содержащей гироскопы , модифицирована таким образом, что устройство действует так, как если бы оно было прикреплено к такому маятнику, удерживая платформу всегда обращенной вниз, когда транспортное средство движется по изогнутой поверхности. Земля.
Спаренные маятники [ править ]


В 1665 году Гюйгенс сделал любопытное наблюдение о маятниковых часах. были помещены двое часов На его мантию , и он заметил, что они приобрели противоположный ход. То есть их маятники бились в унисон, но в противоположном направлении; 180° Смещение по фазе на . Независимо от того, как были запущены два часа, он обнаружил, что они в конечном итоге вернутся в это состояние, сделав, таким образом, первое зарегистрированное наблюдение связанного осциллятора . [136]
Причиной такого поведения было то, что два маятника влияли друг на друга посредством небольших движений поддерживающей мантии. Этот процесс в физике называется увлечением или синхронизацией мод и наблюдается в других связанных генераторах. Синхронизированные маятники использовались в часах и широко использовались в гравиметрах в начале 20 века. Хотя Гюйгенс наблюдал только противофазную синхронизацию, недавние исследования показали существование синфазной синхронизации, а также состояний «смерти», при которых одни или оба часа останавливаются. [137] [138]
Религиозная практика [ править ]

Маятниковое движение появляется и в религиозных церемониях. Качающаяся курильница , называемая курильницей , также известная как кадило , является примером маятника. [139] Маятники также можно увидеть на многих собраниях в восточной Мексике, где они отмечают поворот прилива в тот день, когда приливы достигают своей высшей точки. См. также маятники для гадания и лозоходства .
Образование [ править ]
Маятники широко используются в естественнонаучном образовании как пример гармонического осциллятора для обучения динамике и колебательному движению . Одно из применений — демонстрация закона сохранения энергии . [140] [141] Тяжелый предмет, например шар для боулинга. [142] или разрушающий шар [140] прикреплен к веревке. Затем груз перемещают на расстояние нескольких дюймов от лица добровольца, затем отпускают и позволяют раскачиваться и возвращаться обратно. В большинстве случаев груз меняет направление, а затем возвращается (почти) в то же положение, что и исходное место выброса, т. е . на небольшое расстояние от лица добровольца, оставляя, таким образом, добровольца невредимым. Иногда волонтер получает травму, если волонтер не стоит на месте. [143] или маятник сначала отпускают толчком (так что при возвращении он превосходит положение отпускания).
Устройство для пыток [ править ]

Утверждается, что маятник использовался испанской инквизицией в качестве и казней . орудия пыток [144] в 18 веке. Обвинение содержится в книге 1826 года « История инквизиции Испании» испанского священника, историка и либерального активиста Хуана Антонио Льоренте . [145] Качающийся маятник, край которого представляет собой лезвие ножа, медленно опускается к связанному заключенному, пока не врезается в его тело. [146] Этот метод пыток пришел в общественное сознание благодаря рассказу По « Яма и маятник » 1842 года. американского писателя Эдгара Аллана [147] но существует значительный скептицизм в отношении того, что его действительно использовали.
Большинство осведомленных источников скептически относятся к тому, что эта пытка вообще когда-либо применялась. [148] [149] [150] Единственным свидетельством его использования является один абзац в предисловии к «Истории» Льоренте 1826 года : [145] рассказывает рассказ из вторых рук одного заключенного, освобожденного из мадридской темницы инквизиции в 1820 году, который якобы описал метод пыток маятником. Современные источники отмечают, что из-за предостережения Иисуса против кровопролития инквизиторам было разрешено использовать только те методы пыток, которые не проливали кровь, а метод маятника нарушил бы это ограничение. Одна из теорий состоит в том, что Льоренте неправильно понял услышанное; на самом деле заключенный имел в виду еще одну распространенную пытку инквизиции - страппадо (гарруча), при которой заключенному связывают руки за спиной и поднимают с пола с помощью веревки, привязанной к его рукам. [150] Этот метод также был известен как «маятник». Популярная страшилка По и осведомленность общественности о других жестоких методах инквизиции сохранили миф об этом сложном методе пыток.
Волна маятника [ править ]
— Волна маятника это демонстрация физики и кинетического искусства, состоящая из нескольких несвязанных маятников разной длины. Когда маятники колеблются, они создают бегущие и стоячие волны, биение и хаотическое движение. [151]
См. также [ править ]
- маятники Бартона
- Маятник Блэкберна
- Конический маятник
- Циклоидальный маятник
- Двойной маятник
- Двойной перевернутый маятник
- маятник Дубочинского
- Маятник Фуко
- Украденный кулон
- Решетчатый маятник
- Гармонограф (он же «маятник Лиссажу»)
- Маятник с инерционным колесом
- Перевернутый маятник
- маятник Капицы
- Kater's pendulum
- Метроном
- N-маятник [152]
- Маятник (механика)
- Маятниковые часы
- Ошибка маятниковой ракеты
- Столько же, сколько маятник
- Маятник Рэлея – Лоренца
- Секундный маятник
- Простое гармоническое движение
- Сферический маятник
- Пружинный маятник
- Крутильный маятник
Примечания [ править ]
Значение g, отражаемое периодом маятника, варьируется от места к месту. Гравитационная сила меняется в зависимости от расстояния от центра Земли, т.е. с высотой – или потому, что форма Земли сплюснута, g меняется в зависимости от широты.Более важная причина этого уменьшения g на экваторе заключается в том, что экватор вращается со скоростью один оборот в день, поэтому ускорение гравитационной силы там частично компенсируется центробежной силой .
Ссылки [ править ]
- ^ "Маятник". Университетская энциклопедия Мириам Вебстер . Мириам Вебстер. 2000. с. 1241. ИСБН 978-0-87779-017-4 .
- ^ Jump up to: Перейти обратно: а б с д и ж г Маррисон, Уоррен (1948). «Эволюция кварцевых часов» . Технический журнал Bell System . 27 (3): 510–588. дои : 10.1002/j.1538-7305.1948.tb01343.x . Архивировано из оригинала 17 июля 2011 г.
- ^ Моррис, Уильям, Эд. (1979). Словарь американского наследия, New College Ed . Нью-Йорк: Хоутон-Миффлин. п. 969 . ISBN 978-0-395-20360-6 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ определено Кристианом Гюйгенсом: Гюйгенс, Кристиан (1673). «Horologium Oscillatorium» (PDF) . Математика 17 века . 17th Centurymaths.com . Проверено 1 марта 2009 г. , Часть 4, Определение 3, перевод Яна Брюса, июль 2007 г.
- ^ Jump up to: Перейти обратно: а б Нейв, Карл Р. (2006). «Простой маятник» . Гиперфизика . Государственный университет Джорджии . Проверено 10 декабря 2008 г.
- ^ Сюэ, Линьвэй (2007). «Маятниковые системы» . Видеть и трогать структурные концепции . Кафедра гражданского строительства, унив. Манчестера, Великобритания . Проверено 10 декабря 2008 г.
- ^ Вайсштейн, Эрик В. (2007). «Простой маятник» . Мир науки Эрика Вайсштейна . Вольфрамовые исследования . Проверено 9 марта 2009 г.
- ^ Jump up to: Перейти обратно: а б с д и ж г час я Милхэм, Уиллис И. (1945). Время и хронометристы . Макмиллан. , стр.188-194
- ^ Холлидей, Дэвид; Роберт Резник; Джерл Уокер (1997). Основы физики, 5-е изд . Нью-Йорк: Джон Уайли и сыновья. п. 381 . ISBN 978-0-471-14854-8 .
- ^ Купер, Герберт Дж. (2007). Научные инструменты . Нью-Йорк: Хатчинсон. п. 162. ИСБН 978-1-4067-6879-4 .
- ^ Jump up to: Перейти обратно: а б Нельсон, Роберт; М.Г. Олссон (февраль 1987 г.). «Маятник – богатая физика из простой системы» (PDF) . Американский журнал физики . 54 (2): 112–121. Бибкод : 1986AmJPh..54..112N . дои : 10.1119/1.14703 . S2CID 121907349 . Проверено 29 октября 2008 г.
- ^ Пендерел-Бродхерст, Джеймс Джордж Джозеф (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 06 (11-е изд.). Издательство Кембриджского университета. стр. 536–553, см. стр. 538.
Маятник. Предположим, что у нас есть тело...
включает вывод - ^ Дешен, Дж.С.; Костюмы, БХ (2008). «Висячий шнур с настоящей массой на конце». Европейский журнал физики . 29 (6): 1211–1222. Бибкод : 2008EJPh...29.1211D . дои : 10.1088/0143-0807/29/6/010 . S2CID 122637957 .
- ^ Jump up to: Перейти обратно: а б Гюйгенс, Кристиан (1673). «Часовой осцилляторий» . Математика 17 века . Перевод Брюса, Яна. 17th Centurymaths.com . Проверено 1 марта 2009 г. , часть 4, предложение 5
- ^ Глазго, Дэвид (1885). Изготовление часов и часов . Лондон: Cassel & Co. 278 .
- ^ Фаулз, Грант Р. (1986). Аналитическая механика, 4-е изд . Нью-Йорк, Нью-Йорк: Сондерс. стр. 202 и далее.
- ^ Jump up to: Перейти обратно: а б с Гюйгенс (1673) Колебательные часы , Часть 4, Предложение 20
- ^ Мортон, В. Скотт и Чарльтон М. Льюис (2005). Китай: его история и культура. Нью-Йорк: McGraw-Hill, Inc., с. 70
- ^ Jump up to: Перейти обратно: а б Нидэм, том 3, 627–629.
- ^ Хорошо, Грегори (1998). Науки о Земле: Энциклопедия событий, людей и явлений . Рутледж. п. 394. ИСБН 978-0-8153-0062-5 .
- ^ "ibn+yunus"+pendulum&pg=RA2-PA126 "Маятник" . Американская энциклопедия . Том. 21. Американская корпорация, 1967. с. 502. ИСБН 978-0-19-538207-5 . Проверено 20 февраля 2009 г.
- ^ Бейкер, Сирил Кларенс Томас (1961). Словарь математики . Г. Ньюнс. п. 176.
- ^ Ньютон, Роджер Г. (2004). Маятник Галилея: от ритма времени к созданию материи . США: Издательство Гарвардского университета. п. 52 . ISBN 978-0-674-01331-5 .
- ^ Кинг, Д.А. (1979). «Ибн Юнус и маятник: история ошибок». Международные архивы истории наук . 29 (104): 35–52. , перепечатано на сайте «Мусульманское наследие» .
- ^ Холл, Берт С. (сентябрь 1978 г.). «Схоластический маятник». Анналы науки . 35 (5): 441–462. дои : 10.1080/00033797800200371 . ISSN 0003-3790 .
- ^ О'Коннор, Джей-Джей; Робертсон, EF (ноябрь 1999 г.). «Абу'л-Хасан Али ибн Абд ар-Рахман ибн Юнус» . Университет Сент-Эндрюс . Проверено 29 мая 2007 г.
- ^ Акьемпонг, Эммануэль К.; Гейтс, Генри Луи (2012). "ibn+yunus"+pendulum&pg=RA2-PA126 Африканский биографический словарь, Vol. 1 . Оксфордский университет. Нажимать. п. 126. ИСБН 9780195382075 .
- ^ Мэтьюз, Майкл Р. (2000). Время научного образования . Спрингер. п. 87. ИСБН 978-0-306-45880-4 .
- ^ Дрейк, Стиллман (2003). Галилей за работой: Его научная биография . США: Курьер Дувр. стр. 20–21. ISBN 978-0-486-49542-2 .
- ^ Галилей, Галилей; Драбкин, ИП; Дрейк, Стиллман (1960). О движении и о механике . Мэдисон: Университет Висконсина. п. 108.
- ^ Дрейк, Стиллман (2003). Галилей за работой: Его научная биография . США: Курьер Дувр. п. 17. ISBN 978-0-486-49542-2 .
- ^ Галилей, Галилей (1909). Фаваро, Антонио [на итальянском языке] (ред.). Галилео Галилея, национальное издание ] Работы (на итальянском языке). Флоренция : Барбера. ISBN 978-88-09-20881-0 .
- ^ Мёрдин, Пол (2008). Полный меридиан славы: опасные приключения в соревновании по измерению Земли . Спрингер. п. 41. ИСБН 978-0-387-75533-5 .
- ^ Лампа Галилея , работа Франческо Малагуцци Валери, для Архива истории искусств, том 6 (1893); редактор Доменико Ньоли; Издательство Danesi, Рим; Страницы 215-218.
- ^ Jump up to: Перейти обратно: а б Ван Хелден, Альберт (1995). «Маятниковые часы» . Проект Галилео . Райс Унив . Проверено 25 февраля 2009 г.
- ^ Биготти, Фабрицио; Тейлор, Дэвид (2017). «Пульсилогиум Санторио: новый взгляд на технологии и измерения в ранней современной медицине» . Societate Si Politica . 11 (2): 53–113. ISSN 1843-1348 . ПМК 6407692 . ПМИД 30854144 .
- ^ Дрейк 2003 , стр.419–420.
- ^ хотя есть необоснованные ссылки на предыдущие маятниковые часы, сделанные другими: Ашер, Эбботт Пейсон (1988). История механических изобретений . Курьер Дувр. стр. 310–311. ISBN 978-0-486-25593-4 .
- ^ Эйдсон, Джон К. (2006). Измерение, управление и связь с использованием IEEE 1588 . Буркхаузен. п. 11. ISBN 978-1-84628-250-8 .
- ^ Милхэм 1945, стр.145
- ^ Jump up to: Перейти обратно: а б О'Коннор, Джей-Джей; Э. Ф. Робертсон (август 2002 г.). «Роберт Гук» . Биографии, Архив истории математики MacTutor . Школа математики и статистики, Univ. Сент-Эндрюс, Шотландия. Архивировано из оригинала 3 марта 2009 г. Проверено 21 февраля 2009 г.
- ^ Науенберг, Майкл (2006). «Основной вклад Роберта Гука в орбитальную динамику». Роберт Гук: Исследования трехсотлетия . Издательство Эшгейт. стр. 17–19. ISBN 0-7546-5365-Х .
- ^ Науенберг, Майкл (2004). «Гук и Ньютон: предсказание планетарных движений» . Физика сегодня . 57 (2): 13. Бибкод : 2004ФТ....57б..13Н . дои : 10.1063/1.1688052 . Проверено 30 мая 2007 г.
- ^ Группа компаний КГМ, Инк. (2004 г.). «Гелиоцентрические модели» . Магистр наук. Архивировано из оригинала 13 июля 2007 г. Проверено 30 мая 2007 г.
- ^ Ленцен, Виктор Ф.; Роберт П. Мультауф (1964). «Документ 44: Развитие гравитационных маятников в 19 веке» . Бюллетень 240 Национального музея США: Материалы Музея истории и технологий перепечатаны в Бюллетене Смитсоновского института . Вашингтон: Издательство Смитсоновского института. п. 307 . Проверено 28 января 2009 г.
- ^ Ричер, Жан (1679). Астрономические и физические наблюдения, произведенные на острове Кайенна . Мемуары Королевской академии наук. Бибкод : 1679oaep.book.....R . цитируется по Lenzen & Multauf, 1964 , стр.307.
- ^ Ленцен и Мультауф, 1964 , стр.307.
- ^ Пойнтинг, Джон Генри; Джозеф Джон Томпсон (1907). Учебник физики, 4-е изд . Лондон: Charles Griffin & Co., стр. 20–22 .
- ^ Гюйгенс, Кристиан; перевод Яна Брюса (июль 2007 г.). «Horologium Oscillatorium» (PDF) . Математика 17 века . 17th Centurymaths.com . Проверено 1 марта 2009 г.
- ↑ созвездие Часов . В честь этой книги позже было названо
- ^ Мэтьюз, Майкл Р. (1994). Преподавание естественных наук: роль истории и философии науки . Психология Пресс. стр. 121–122. ISBN 978-0-415-90899-3 .
- ^ Гюйгенс, Колебательные часы , Часть 2, Предложение 25
- ^ Махони, Майкл С. (19 марта 2007 г.). «Христиан Гюйгенс: измерение времени и долготы на море» . Принстонский университет. Архивировано из оригинала 4 декабря 2007 года . Проверено 27 мая 2007 г.
- ^ Бевилаква, Фабио; Лидия Фаломо; Лусио Фрегонезе; Энрико Джанетто; Франко Джудизе; Паоло Маскеретти (2005). «Маятник: от вынужденного падения к концепции потенциала» . Маятник: научные, исторические, философские и образовательные перспективы . Спрингер. стр. 195–200. ISBN 1-4020-3525-Х . Проверено 26 февраля 2008 г. дает подробное описание методов Гюйгенса.
- ^ Jump up to: Перейти обратно: а б Хедрик, Майкл (2002). «Происхождение и эволюция спускового механизма якорных часов» . Журнал «Системы управления», Inst. Инженеров по электротехнике и электронике . 22 (2). Архивировано из оригинала 25 октября 2009 года . Проверено 6 июня 2007 г.
- ^ " ...на это влияет либо невоздержание воздуха, либо какие-либо неисправности в механизме, поэтому QR-костыль не всегда активируется одной и той же силой... При больших дугах качания занимают больше времени, как я объяснил , следовательно, по этой причине существуют некоторые неравенства в движении часов... ", Гюйгенс, Христиан (1658). Часы (PDF) . Гаага: Адриан Влак. , перевод Эрнеста Л. Эдвардса (декабрь 1970 г.) Antiquarian Horology , Vol.7, No.1
- ^ Jump up to: Перейти обратно: а б Эндрюс, WJH Часы: скачок к точности в Мейси, Сэмюэл (1994). Энциклопедия времени . Тейлор и Фрэнсис. стр. 123–125. ISBN 978-0-8153-0615-3 .
- ^ Ашер, 1988 , стр.312.
- ^ Jump up to: Перейти обратно: а б Беккет, Эдмунд (1874). Элементарный трактат о часах, часах и колоколах, 6-е изд . Лондон: Lockwood & Co., с. 50.
- ^ Jump up to: Перейти обратно: а б Грэм, Джордж (1726). «Устройство, позволяющее избежать неравномерностей в движении часов, вызванных действием тепла и холода на стержень маятника» . Философские труды Королевского общества . 34 (392–398): 40–44. дои : 10.1098/rstl.1726.0006 . S2CID 186210095 . цитируется в Дэй, Лэнс; Ян МакНил (1996). Биографический словарь истории техники . Тейлор и Фрэнсис. п. 300. ИСБН 978-0-415-06042-4 .
- ^ Jump up to: Перейти обратно: а б Катер, Генри (1818). «Отчет об экспериментах по определению продолжительности секунд колебаний маятника на широте Лондона» . Фил. Пер. Р. Сок . 104 (33): 109 . Проверено 25 ноября 2008 г.
- ^ Опрея, Джон (1995). «Геометрия и маятник Фо» (PDF) . Американский математический ежемесячник . 102 (6). Математическая ассоциация Америки: 515–522. дои : 10.1080/00029890.1995.12004611 . Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 13 апреля 2021 г.
- ^ Амир Аксель (2003) Леон Фуко: Его жизнь, времена и достижения, в Мэтьюз, Майкл Р.; Колин Ф. Голд; Артур Стиннер (2005). Маятник: научные, исторические, образовательные и философские перспективы . Спрингер. п. 177. ИСБН 978-1-4020-3525-8 .
- ^ Джованнанжели, Франсуаза (ноябрь 1996 г.). «Вращающийся маятник Фуко в Пантеоне» . Парижские страницы. Архивировано из оригинала 9 июня 2007 г. Проверено 25 мая 2007 г.
- ^ Тобин, Уильям (2003). Жизнь и наука Леона Фуко: Человек, доказавший, что Земля вращается . Великобритания: Издательство Кембриджского университета. стр. 148–149. ISBN 978-0-521-80855-2 .
- ^ Jump up to: Перейти обратно: а б с д Пендерел-Бродхерст, Джеймс Джордж Джозеф (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 06 (11-е изд.). Издательство Кембриджского университета. стр. 536–553, см. стр. 540 и 541.
- ^ Jump up to: Перейти обратно: а б с Джонс, Тони (2000). Разделение секунды: история атомного времени . ЦРК Пресс. п. 30. ISBN 978-0-7503-0640-9 .
- ^ Калер, Джеймс Б. (2002). Постоянно меняющееся небо: Путеводитель по небесной сфере . Великобритания: Кембриджский университет. Нажимать. п. 183. ИСБН 978-0-521-49918-7 .
- ^ Одуэн, Клод; Бернар Гино; Стивен Лайл (2001). Измерение времени: время, частота и атомные часы . Великобритания: Кембриджский университет. Нажимать. п. 83. ИСБН 978-0-521-00397-1 .
- ^ Jump up to: Перейти обратно: а б Торге, Вольфганг (2001). Геодезия: Введение . Вальтер де Грюйтер. п. 177. ИСБН 978-3-11-017072-6 .
- ^ Милхэм 1945, стр.334
- ^ рассчитано по уравнению (1)
- ^ Глазго, Дэвид (1885). Изготовление часов и часов . Лондон: Кассель и Ко, стр. 279–284 .
- ^ Мэттис, Роберт Дж. (2004). Точные маятниковые часы . Великобритания: Оксфордский университет. Нажимать. п. 4. ISBN 978-0-19-852971-2 .
- ^ Маттейс, 2004, с. 13
- ^ Маттис 2004 , стр.91-92.
- ^ Беккет 1874 , стр.48
- ^ «Регулирование» . Энциклопедия часов . Рынок старого и проданного антиквариата. 2006 год . Проверено 9 марта 2009 г.
- ^ Беккет 1874 , стр.43
- ^ Глазго 1885 , стр.282.
- ^ «Факты о Великих часах» . Биг Бен . Лондон: Парламент Великобритании. 13 ноября 2009 г. Архивировано из оригинала 7 октября 2009 г. . Проверено 31 октября 2012 г.
- ^ Маттис 2004 , стр.3
- ^ Jump up to: Перейти обратно: а б с д Пендерел-Бродхерст, Джеймс Джордж Джозеф (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 06 (11-е изд.). Издательство Кембриджского университета. стр. 536–553, см. стр. 539 и 540.
- ^ Гюйгенс, Христиан (1658). Часы (PDF) . Гаага: Адриан Влак. , перевод Эрнеста Л. Эдвардса (декабрь 1970 г.) Antiquarian Horology , Vol.7, No.1
- ^ Зупко, Рональд Эдвард (1990). Революция в измерениях: западноевропейские меры и веса со времен науки . Издательство Диана. п. 131. ИСБН 978-0-87169-186-6 .
- ^ Пикард, Жан (1671). La Mesure de la Terre [ Измерение Земли ] (на французском языке). Париж, Франция: Imprimerie Royale. п. 4. Пикард описал маятник, состоящий из медного шара диаметром дюйм (2,54 мм), подвешенного на нити пита — волокна растения алоэ. Затем Пикард упоминает, что температура незначительно влияет на длину этого маятника: «Il est vray que cette longueur ne s'est pas toûjours trouvées si точные, & qu'il a semblé qu'elle devoit estre toûjours un peu Accourcie en Hyver, & allongée en esté; mais c'est seulement de la dixieme partie d'une ligne ...» («Это правда, что эта длина [маятника] не всегда оказывается [] столь точной, и кажется, что она такова». зимой всегда должна быть немного укорочена, а летом удлиннена, но это лишь на десятую часть линии...") [1 ligne (линия) = 2,2558 мм].
- ^ Jump up to: Перейти обратно: а б с д Маттис 2004 , стр.7-12.
- ^ Милхэм 1945, стр.335
- ^ Милхэм 1945, стр.331-332.
- ^ Маттис 2004 , Часть 3, стр.153-179.
- ^ Пойнтинг и Томпсон, 1907, стр.13-14.
- ^ Апдеграфф, Милтон (7 февраля 1902 г.). «Об измерении времени» . Наука . 15 (371): 218–219. doi : 10.1126/science.ns-15.374.218-a . ПМИД 17793345 . S2CID 21030470 . Проверено 13 июля 2009 г.
- ^ Данвуди, Хэлси (1917). Заметки, задачи и лабораторные упражнения по механике, звуку, свету, термомеханике и гидравлике, 1-е изд . Нью-Йорк: Джон Уайли и сыновья. п. 87.
- ^ «Ширина резонанса» . Глоссарий . Отдел времени и частоты, Национальный институт стандартов и технологий США. 2009. Архивировано из оригинала 30 января 2009 г. Проверено 21 февраля 2009 г.
- ^ Jump up to: Перейти обратно: а б Джесперсен, Джеймс; Фитц-Рэндольф, Джейн; Робб, Джон (1999). От солнечных часов до атомных часов: понимание времени и частоты . Нью-Йорк: Курьер Дувр. стр. 41–50. ISBN 978-0-486-40913-9 . стр.39
- ^ Мэттис, Роберт Дж. (2004). Точные маятниковые часы . Великобритания: Оксфордский университет. Нажимать. стр. 27–36. ISBN 978-0-19-852971-2 . имеет превосходное всестороннее обсуждение споров по поводу применимости Q к точности маятников.
- ^ «Показатель качества, Q» . Глоссарий . Отдел времени и частоты, Национальный институт стандартов и технологий США. 2009. Архивировано из оригинала 4 мая 2008 г. Проверено 21 февраля 2009 г.
- ^ Маттис, 2004, стр.32, рис. 7.2 и текст
- ^ Маттис, 2004, стр.81.
- ^ Jump up to: Перейти обратно: а б с «Q, Фактор качества» . Журнал «Часы и часы» . Сайт Орологерии Ламберлина . Проверено 21 февраля 2009 г.
- ^ Милхэм 1945, стр.615
- ^ «Часы Райфлера и Шортта» . Институт времени и технологий JagAir . Проверено 29 декабря 2009 г.
- ^ Беттс, Джонатан (22 мая 2008 г.). «Заявление эксперта, случай 6 (2008-09) регулятор Уильяма Гамильтона Шортта» . Слушания по вопросу лицензирования экспорта, Наблюдательная комиссия по экспорту произведений искусства и предметов культурного интереса . Совет музеев, библиотек и архивов Великобритании. Архивировано из оригинала (DOC) 25 октября 2009 года . Проверено 29 декабря 2009 г.
- ^ Эйри, Джордж Биддл (26 ноября 1826 г.). «О возмущениях маятников и весов и теории спусков» . Труды Кембриджского философского общества . 3 (Часть 1): 105 . Проверено 25 апреля 2008 г.
- ^ Беккет 1874 , стр.75-79.
- ^ Вочадло, Лидунка. «Гравитация, форма Земли, изостазия, момент инерции» . Проверено 5 ноября 2012 г.
- ^ Бейкер, Лайман А. (весна 2000 г.). «Канцлер Бэкон» . Английский 233 – Введение в западные гуманитарные науки . Кафедра английского языка, Университет штата Канзас . Проверено 20 февраля 2009 г.
- ^ Jump up to: Перейти обратно: а б Пойнтинг и Томпсон, 1907, стр. 9.
- ^ Пойнтинг, Джон Генри; Джозеф Джон Томпсон (1907). Учебник физики, 4-е изд . Лондон: Charles Griffin & Co., с. 20 .
- ^ Jump up to: Перейти обратно: а б Виктор Ф., Ленцен; Роберт П. Мультауф (1964). «Документ 44: Развитие гравитационных маятников в 19 веке» . Бюллетень 240 Национального музея США: Материалы Музея истории и технологий перепечатаны в Бюллетене Смитсоновского института . Вашингтон: Издательство Смитсоновского института. п. 307 . Проверено 28 января 2009 г.
- ^ Jump up to: Перейти обратно: а б Пойнтинг и Томпсон, 1907, стр.10.
- ^ Пойнтинг, Джон Генри (1894). Средняя плотность Земли . Лондон: Чарльз Гриффин. стр. 22–24 .
- ^ Кокс, Джон (1904). Механика . Кембридж, Великобритания: Кембриджский университет. Нажимать. стр. 311–312 .
- ^ Пойнтинг и Томсон 1904, стр.23
- ^ Пойнтинг, Джон Генри (1894). Средняя плотность Земли . Лондон: Charles Griffin & Co., стр. 24–29 .
- ^ Пойнтинг, Джон Генри (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 12 (11-е изд.). Издательство Кембриджского университета. стр. 384–389, см. стр. 386.
Эксперимент Эйри. — В 1854 году сэр Г.Б. Эйри…
- ^ Ленцен и Мультауф 1964, стр.320
- ^ Пойнтинг и Томпсон 1907, стр.18
- ^ Jump up to: Перейти обратно: а б с «Пады и взлеты гравиметрических исследований» . НОАА отмечает 200-летие . Национальное управление океанографии и атмосферы США. 09.07.2007.
- ^ Ленцен и Мультауф 1964, стр.324
- ^ Ленцен и Мультауф 1964, стр.329
- ^ Jump up to: Перейти обратно: а б Вулард, Джордж П. (28–29 июня 1957 г.). «Гравитационные наблюдения во время МГГ» . Геофизика и МГГ: Материалы симпозиума по случаю открытия Международного геофизического года . Вашингтон, округ Колумбия: Американский геофизический союз, Национальная академия наук. п. 200 . Проверено 27 мая 2009 г.
- ^ Ленцен и Мультауф 1964, стр.336, рис.28.
- ^ Jump up to: Перейти обратно: а б Майкл Р., Мэтьюз (2001). «Методология и политика в науке: судьба предложения Гюйгенса 1673 года о маятнике как международного стандарта длины и некоторые образовательные предложения» . Наука, образование и культура: вклад истории и философии науки . Спрингер. п. 296. ИСБН 0-7923-6972-6 .
- ^ Ренвик, Джеймс (1832). Элементы механики . Филадельфия: Кэри и Леа. стр. 286–287 .
- ^ Олдер, Кен (2003). Мера всех вещей: Семилетняя одиссея и скрытая ошибка, изменившая мир . США: Саймон и Шустер. п. 88. ИСБН 978-0-7432-1676-0 .
- ^ цитируется в Журдан, Луи (22 октября 2001 г.). «Re: СИ и словари» . USMA (список рассылки) . Проверено 27 января 2009 г.
- ^ Аньоли, Паоло; Джулио Д'Агостини (декабрь 2004 г.). «Почему метр бьет второй?». arXiv : физика/0412078 .
- ^ цитируется в ЛеКонте, Джон (август 1885 г.). «Метрическая система» . Оверленд Ежемесячник . 6 (2): 178 . Проверено 4 марта 2009 г.
- ^ Зупко, 1990, с.131.
- ^ Зупко, 1990, с.140-141.
- ^ Зупко, 1990, стр.93.
- ^ Шумахер, Генрих (1821). «Датский стандарт длины» . Ежеквартальный журнал науки, литературы и искусства . 11 (21): 184–185 . Проверено 17 февраля 2009 г.
- ^ «Шумахер, Генрих Кристиан» . Американская циклопедия . Том. 14. Д. Эпплтон и Ко, Лондон. 1883. с. 686 . Проверено 17 февраля 2009 г.
- ^ Траутвайн, Джон Крессон (1907). Карманный справочник инженера-строителя, 18-е изд . Нью-Йорк: Джон Уайли. п. 216.
- ^ Тун, Джон (8 сентября 2000 г.). «Вне времени: исследователи воссоздают эксперимент с часами 1665 года, чтобы получить представление о современных синхронизированных генераторах» . Технологический институт Джорджии . Проверено 31 мая 2007 г.
- ^ А. Л. Фрадков и Б. Андриевский, "Синхронизация и фазовые соотношения в движении двухмаятниковой системы", Международный журнал нелинейной механики, том. 42 (2007), стр. 895–901.
- ^ И.И. Блехман, «Синхронизация в науке и технике», ASME Press, Нью-Йорк, 1988, (перевод с русского на английский)
- ^ Интересную симуляцию движения кадильницы можно найти на этом сайте. Архивировано 23 мая 2011 г. в Wayback Machine .
- ^ Jump up to: Перейти обратно: а б Харт, Мэтью (2 февраля 2016 г.). «Физика рискует умереть, если сломает мяч ради науки» . Нердист . Архивировано из оригинала 15 марта 2017 года . Проверено 14 марта 2017 г.
- ^ Соренсон, Рой (2014). «Мысленные эксперименты для новичков» . В Буте, Энтони Роберт; Роуботтом, Даррелл П. (ред.). Интуиции . Оксфордский университет Pr. п. 139. ИСБН 9780199609192 . Проверено 15 марта 2017 г.
- ^ «Маятник из шара для боулинга» . Чудеса физики . Университет Висконсина-Мэдисона . Проверено 14 марта 2017 г.
- ^ weknowmemes (8 августа 2014 г.). «Тест по физике прошел не так» . Ютуб . Архивировано из оригинала 10 ноября 2021 г. Проверено 14 марта 2017 г.
- ^ Скотт, Джордж Райли (2009). История пыток на протяжении веков . Рутледж. п. 242. ИСБН 978-1136191602 .
- ^ Jump up to: Перейти обратно: а б Льоренте, Хуан Антонио (1826). История инквизиции Испании. Сокращено и переведено Джорджем Б. Уиттакером . Оксфордский университет. стр. XX, предисловие.
- ^ Эбботт, Джеффри (2006). Казнь: гильотина, маятник, тысяча порезов, испанский осел и 66 других способов казнить человека . Пресса Святого Мартина. ISBN 978-0-312-35222-6 .
- ^ По, Эдгар Аллан (1842). Яма и маятник . Книжная классика. ISBN 978-9635271900 .
- ^ Рот, Сесил (1964). Испанская инквизиция . WW Нортон и компания. стр. 258 . ISBN 978-0-393-00255-3 .
маятник.
- ^ Манникс, Дэниел П. (2014). История пыток . ЭНет Пресс. п. 76. ИСБН 978-1-61886-751-3 .
- ^ Jump up to: Перейти обратно: а б Павлак, Брайан (2009). Охота на ведьм в западном мире: преследования и наказания со стороны инквизиции на протяжении Салемского процесса . АВС-КЛИО. п. 152. ИСБН 978-0-313-34874-7 .
- ^ Демонстрации лекций Гарвардского университета по естественным наукам, Волны маятника
- ^ Юрченко Д.; Алеврас, П. (2013). «Динамика N-маятника и ее применение к концепции преобразователя волновой энергии» . Международный журнал динамики и управления . 1 (4): 4. дои : 10.1007/s40435-013-0033-x .
Дальнейшее чтение [ править ]
- Г. Л. Бейкер и Дж. А. Блэкберн (2009). Маятник: пример из физики (издательство Оксфордского университета).
- М. Гиттерман (2010). Хаотический маятник (World Scientific).
- Майкл Р. Мэтьюз, Артур Стиннер, Колин Ф. Голд (2005) Маятник: научные, исторические, философские и образовательные перспективы , Спрингер
- Мэтьюз, Майкл Р.; Голд, Колин; Стиннер, Артур (2005). «Маятник: его место в науке, культуре и педагогике». Наука и образование . 13 (4/5): 261–277. Бибкод : 2004Sc&Ed..13..261M . doi : 10.1023/b:sced.0000041867.60452.18 . S2CID 195221704 .
- Шломо Зильберманн, (2014) «Основы маятника; путь в никуда» (книга)
- Мэттис, Роберт Дж. (2004). Точные маятниковые часы . Великобритания: Оксфордский университет. Нажимать. ISBN 978-0-19-852971-2 .
- Нельсон, Роберт; М.Г. Олссон (февраль 1986 г.). «Маятник – богатая физика из простой системы». Американский журнал физики . 54 (2): 112–121. Бибкод : 1986AmJPh..54..112N . дои : 10.1119/1.14703 . S2CID 121907349 .
- ЛП Пук (2011). Понимание маятников: краткое введение (Спрингер).
Внешние ссылки [ править ]
![]() СМИ, связанные с маятниками, на Викискладе?
СМИ, связанные с маятниками, на Викискладе?
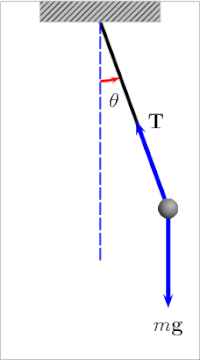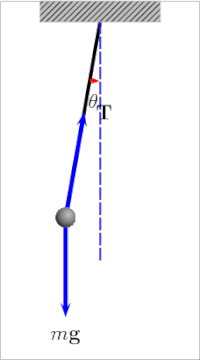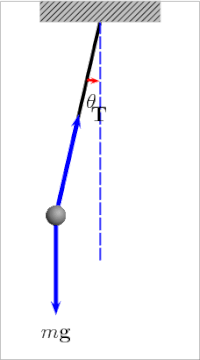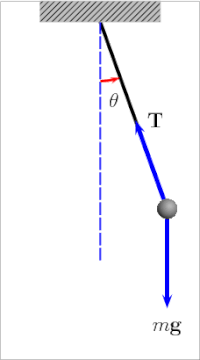







![{\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}\left[\sum _{n=0}^{\infty }\left({\frac {\left(2n\) вправо)!}{2^{2n}\left(n!\right)^{2}}}\right)^{2}\sin ^{2n}\left({\frac {\theta _{0} }{2}}\right)\right]=2\pi {\sqrt {\frac {L}{g}}}\left(1+{\frac {1}{16}}\theta _{0} ^{2}+{\frac {11}{3072}}\theta _{0}^{4}+\cdots \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8421cbd1dd0d5564c5f84120bb9f8a68e7e6312)