Центр удара

Центр удара — это точка на вытянутом массивном объекте, прикрепленном к стержню, где перпендикулярный удар не вызывает реактивного удара по стержню. Поступательные и вращательные движения прекращаются в шарнире, когда импульсивный удар наносится в центр удара. Центр удара часто обсуждается в контексте биты, ракетки , двери, меча или другого вытянутого предмета, удерживаемого за один конец.

Одна и та же точка называется центром колебаний объекта, подвешенного на оси маятника , что означает, что простой маятник, вся его масса сосредоточена в этой точке, будет иметь тот же период колебаний, что и составной маятник.

В спорте центр удара биты, ракетки или клюшки связан с так называемой « сладкой точкой », но последняя также связана с вибрационным изгибом предмета.

Объяснение

Последствия удара по висячей балке. CP — центр удара, а CM — центр масс луча.

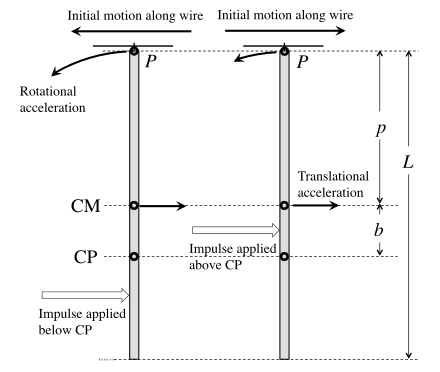
Представьте себе жесткую балку, подвешенную к проволоке с помощью приспособления, которое может свободно скользить по проволоке в точке P, как показано на рисунке. Импульсивный удар наносится слева. Если он находится ниже центра масс (ЦМ), это приведет к вращению луча против часовой стрелки вокруг ЦМ, а также к перемещению ЦМ вправо. Центр перкуссии (ЦП) находится ниже ЦМ. Если удар падает выше CP, поступательное движение вправо будет больше, чем вращательное движение влево в точке P, в результате чего чистое начальное движение приспособления будет вправо. Если удар упадет ниже CP, произойдет обратное: вращательное движение в точке P будет больше, чем поступательное движение, и приспособление сначала переместится влево. Только если удар приходится точно на CP, два компонента движения взаимно компенсируются, создавая нулевое чистое начальное движение в точке P.

Когда скользящее приспособление заменяется шарниром, который не может перемещаться влево или вправо, импульсивный удар где-либо, кроме CP, приводит к возникновению первоначальной реактивной силы на шарнире.

Вычисление центра удара

Для свободной жесткой балки импульс $Fdt$ наносится под прямым углом на расстоянии $b$ от центра масс (ЦМ) приведет к изменению скорости ЦМ $dv_{cm}$ по отношению:

F=M{\frac {dv_{cm}}{dt}},

где $M$ - масса балки. Аналогично, крутящий момент вокруг ЦМ изменит угловую скорость $\omega$ в соответствии с:

Fb=I{\frac {d\omega }{dt}},

где $I$ – момент инерции вокруг ЦМ.

Для любой точки P расстояние $p$ на противоположной от точки удара стороне ЦМ изменение скорости точки Р равно

dv_{net}=dv_{cm}-pd\omega \,

где $p$ - расстояние P от CM. Следовательно, ускорение в точке P из-за импульсивного удара равно:

{\frac {dv_{net}}{dt}}=\left({\frac {1}{M}}-{\frac {pb}{I}}\right)F.

Когда это ускорение равно нулю, $b$ определяет центр удара. Следовательно, расстояние CP, $b$ , из CM, определяется выражением

b={\frac {I}{pM}}.

Обратите внимание, что P, ось вращения, не обязательно должна находиться на конце балки, ее можно выбрать на любом расстоянии. $p$ .

Длина $b+p$ также определяет центр колебаний физического маятника , то есть положение массы простого маятника, имеющего тот же период, что и физический маятник. ^[1]

Центр удара равномерного луча

Для частного случая балки одинаковой плотности по длине $L$ , момент инерции вокруг ЦМ равен:

I={\frac {1}{12}}ML^{2}

( см. в моменте инерции ), доказательство

и для вращения вокруг оси на конце,

p=L/2

.

Это приводит к:

b={\frac {L^{2}}{12p}}={\frac {1}{6}}L

.

Отсюда следует, что ЦП составляет 2/3 длины однородного луча. $L$ от поворотного конца.

Некоторые приложения

Например, распашная дверь, которая останавливается дверным упором, расположенным на 2/3 ширины двери, будет выполнять свою работу с минимальным встряхиванием двери, поскольку шарнирный конец не подвергается результирующей реактивной силе. (Эта точка также является узлом второй вибрационной гармоники, которая также минимизирует вибрацию.)

Наилучшая точка удара бейсбольной битой обычно определяется как точка, в которой удар ощущается бьющим лучше всего. Центр удара определяет место, где, если бита ударяет по мячу и руки бьющего находятся в точке поворота, бьющий не чувствует внезапной реактивной силы. Однако, поскольку бита не является твердым предметом, свою роль также играют вибрации, возникающие при ударе. Кроме того, точка поворота замаха может находиться не в том месте, где находятся руки бьющего. Исследования показали, что доминирующий физический механизм определения наилучшего положения возникает из-за расположения узлов в колебательных режимах летучей мыши, а не из-за местоположения центра удара. ^[2]

Концепция центра удара может быть применена к мечам . Будучи гибкими объектами, «золотая середина» такого режущего оружия зависит не только от центра удара, но также от характеристик изгиба и вибрации. ^[3]^[4]

Ссылки

^ Рассел, Дэниел А. (16 июня 2005 г.). «Что такое КС и имеет ли это значение?» . Физика и акустика бейсбольных и софтбольных бит . Пенсильванский государственный университет . Архивировано из оригинала 5 апреля 2009 года . Проверено 24 мая 2012 г.
^ Кросс, Род (2004). «Центр ударов ручного орудия» (PDF) . Американский журнал физики . 72 (5): 622–630. Бибкод : 2004AmJPh..72..622C . дои : 10.1119/1.1634965 .
^ Тернер, Джордж (1999). «Движения и удары меча: исследование и анализ» . Ассоциация боевых искусств эпохи Возрождения . Проверено 24 мая 2012 г.
^ Гейслер, Роберт (2014). «О динамике мечей» . ХРОАРР. Архивировано из оригинала 05 марта 2021 г. Проверено 30 марта 2021 г.

[1] Рассел, Дэниел А. (16 июня 2005 г.). «Что такое КС и имеет ли это значение?» . Физика и акустика бейсбольных и софтбольных бит . Пенсильванский государственный университет . Архивировано из оригинала 5 апреля 2009 года . Проверено 24 мая 2012 г.

[2] Кросс, Род (2004). «Центр ударов ручного орудия» (PDF) . Американский журнал физики . 72 (5): 622–630. Бибкод : 2004AmJPh..72..622C . дои : 10.1119/1.1634965 .

[Turner-3] Тернер, Джордж (1999). «Движения и удары меча: исследование и анализ» . Ассоциация боевых искусств эпохи Возрождения . Проверено 24 мая 2012 г.

[4] Гейслер, Роберт (2014). «О динамике мечей» . ХРОАРР. Архивировано из оригинала 05 марта 2021 г. Проверено 30 марта 2021 г.

[1]

[2]

[3]

[4]