Столько же, сколько маятник

Квантовый маятник имеет фундаментальное значение для понимания затрудненного внутреннего вращения в химии, квантовых особенностей рассеяния атомов, а также многих других квантовых явлений. Хотя маятнику, не подпадающему под действие приближения малых углов, присуща нелинейность, уравнение Шредингера для квантованной системы можно решить относительно легко.

Уравнение Шрёдингера

Используя лагранжеву механику из классической механики, можно разработать гамильтониан для системы. Простой маятник имеет одну обобщенную координату (угловое смещение $\phi$) и два ограничения (длина струны и плоскость движения). Кинетическая и потенциальная энергии системы могут быть найдены как

$T={\frac {1}{2}}ml^{2}{\dot {\phi }}^{2},$

$U=mgl(1-\cos \phi ).$

Это приводит к гамильтониану

${\hat {H}}={\frac {{\hat {p}}^{2}}{2ml^{2}}}+mgl(1-\cos \phi ).$

Зависящее от времени уравнение Шредингера для системы имеет вид

$i\hbar {\frac {d\Psi }{dt}}=-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {d^{2}\Psi }{d\phi ^{2}}}+mgl(1-\cos \phi )\Psi .$

Чтобы найти уровни энергии и соответствующие им собственные состояния, необходимо решить независимое от времени уравнение Шредингера. Лучше всего это сделать, изменив независимую переменную следующим образом:

$\eta =\phi +\pi ,$

$\Psi =\psi e^{-iEt/\hbar },$

$E\psi =-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {d^{2}\psi }{d\eta ^{2}}}+mgl(1+\cos \eta )\psi .$

Это просто дифференциальное уравнение Матье

${\frac {d^{2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,$

решениями которых являются функции Матье .

Решения

Энергии

Данный $q$, для счетного числа специальных значений $a$, называемые характеристическими значениями , уравнение Матье допускает решения, периодические с периодом $2\pi$. Характеристические значения функций косинуса и синуса Матье соответственно записываются $a_{n}(q),b_{n}(q)$, где $n$ является натуральным числом . Периодические частные случаи функций косинуса и синуса Матье часто записывают $CE(n,q,x),SE(n,q,x)$ соответственно, хотя им традиционно придается иная нормировка (а именно, что их $L^{2}$норма равна $\pi$).

Граничные условия в квантовом маятнике означают, что $a_{n}(q),b_{n}(q)$ для данного $q$:

${\frac {d^{2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,$

$a_{n}(q),b_{n}(q)={\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}.$

Энергии системы, $E=mgl+{\frac {\hbar ^{2}a_{n}(q),b_{n}(q)}{2ml^{2}}}$ для четных/нечетных решений соответственно квантуются на основе характеристических значений, найденных путем решения уравнения Матье.

Эффективную потенциальную глубину можно определить как

$q={\frac {m^{2}gl^{3}}{\hbar ^{2}}}.$

Глубокий потенциал дает динамику частицы в независимом потенциале. Напротив, в мелком потенциале важное значение приобретают волны Блоха , а также квантовое туннелирование .

Общее решение

Общее решение приведенного выше дифференциального уравнения для заданного значения a и q представляет собой набор линейно независимых косинусов и синусов Матье, которые являются четными и нечетными решениями соответственно. В общем случае функции Матье апериодичны; однако для характеристических значений $a_{n}(q),b_{n}(q)$косинус и синус Матье становятся периодическими с периодом $2\pi$.

собственные состояния

Для положительных значений q справедливо следующее:

$C(a_{n}(q),q,x)={\frac {CE(n,q,x)}{CE(n,q,0)}},$

$S(b_{n}(q),q,x)={\frac {SE(n,q,x)}{SE'(n,q,0)}}.$

Вот несколько первых периодических косинусных функций Матье для $q=1$.

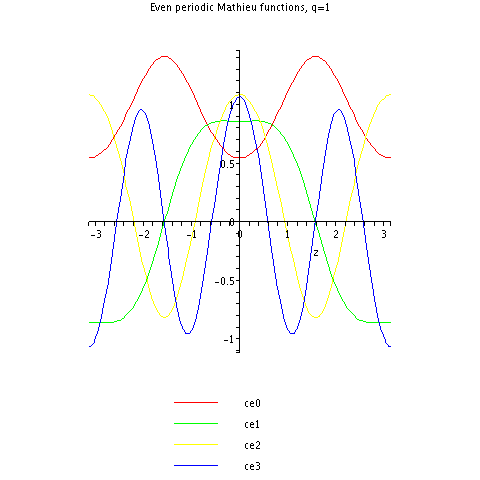
Обратите внимание, что, например, $CE(1,1,x)$ (зеленый) напоминает функцию косинуса, но с более плоскими холмами и более мелкими долинами.

См. также

• Квантовый гармонический осциллятор

Библиография

• Брансден, Британская Колумбия; Хоахейн, CJ (2000). Квантовая механика (2-е изд.). Эссекс: Pearson Education. ISBN  0-582-35691-1 .
• Дэвис, Джон Х. (2006). Физика низкоразмерных полупроводников: Введение (6-е переиздание). Издательство Кембриджского университета. ISBN  0-521-48491-Х .
• Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Прентис Холл. ISBN  0-13-111892-7 .
• Мухаммад Аюб, Квантовый маятник атомной оптики , 2011, Исламабад, Пакистан, https://arxiv.org/abs/1012.6011