Распространение Гумбеля

Гумбель

Функция плотности вероятности
Кумулятивная функция распределения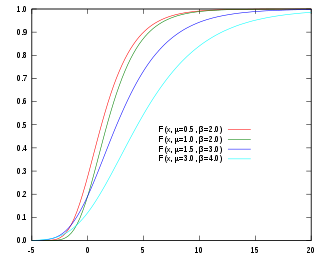
Обозначения	${\text{Gumbel}}(\mu ,\beta )$
Параметры	$\mu ,$ местоположение ( реальное ) $\beta >0,$ масштаб (реальный)
Поддерживать	$x\in \mathbb {R}$
PDF	${\frac {1}{\beta }}e^{-(z+e^{-z})}$ где $z={\frac {x-\mu }{\beta }}$
CDF	$e^{-e^{-(x-\mu )/\beta }}$
Квантиль	$\mu -\beta \ln(-\ln(p))$
Иметь в виду	$\mu +\beta \gamma$ где $\gamma$ постоянная Эйлера -Машерони
медиана	$\mu -\beta \ln(\ln 2)$
Режим	$\mu$
Дисперсия	${\frac {\pi ^{2}}{6}}\beta ^{2}$
асимметрия	${\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1.14$
Избыточный эксцесс	${\frac {12}{5}}$
Энтропия	$\ln(\beta )+\gamma +1$
МГФ	$\Gamma (1-\beta t)e^{\mu t}$
CF	$\Gamma (1-i\beta t)e^{i\mu t}$

В теории вероятностей и статистике распределение Гамбеля (также известное как типа I обобщенное распределение экстремальных значений ) используется для моделирования распределения максимума (или минимума) ряда выборок различных распределений.

Это распределение можно было бы использовать для представления распределения максимального уровня реки в конкретном году, если бы существовал список максимальных значений за последние десять лет. Это полезно для прогнозирования вероятности возникновения сильного землетрясения, наводнения или другого стихийного бедствия. Потенциальная применимость распределения Гамбеля для представления распределения максимумов связана с теорией экстремальных значений , которая указывает на то, что оно может быть полезным, если распределение основных выборочных данных имеет нормальный или экспоненциальный тип.

Распределение Гамбеля является частным случаем обобщенного распределения экстремальных значений (также известного как распределение Фишера – Типпетта). Оно также известно как логарифмическое распределение Вейбулла и двойное экспоненциальное распределение (термин, который альтернативно иногда используется для обозначения распределения Лапласа ). Это связано с распределением Гомпертца : когда его плотность сначала отражается относительно начала координат, а затем ограничивается положительной полупрямой, получается функция Гомпертца.

В формулировке латентной переменной полиномиальной логит- модели, распространенной в теории дискретного выбора , ошибки латентных переменных подчиняются распределению Гамбеля. Это полезно, поскольку разница двух случайных величин , распределенных по Гамбелу, имеет логистическое распределение .

Распределение Гамбеля названо в честь Эмиля Юлиуса Гамбеля (1891–1966) на основе его оригинальных статей, описывающих это распределение.

Определения

Кумулятивная функция распределения распределения Гамбеля равна

$F(x;\mu ,\beta )=e^{-e^{-(x-\mu )/\beta }}\,$

Стандартное распространение Gumbel

Стандартное распределение Гамбеля — это случай, когда $\mu =0$ и $\beta =1$ с кумулятивной функцией распределения

$F(x)=e^{-e^{(-x)}}\,$

и функция плотности вероятности

$f(x)=e^{-(x+e^{-x})}.$

В этом случае мода равна 0, медиана равна $-\ln(\ln(2))\approx 0.3665$, среднее значение $\gamma \approx 0.5772$ ( константа Эйлера-Машерони ), а стандартное отклонение равно $\pi /{\sqrt {6}}\approx 1.2825.$

Кумулянты для > 1 n имеют вид

$\kappa _{n}=(n-1)!\zeta (n).$

Характеристики

Мода равна µ, а медиана равна $\mu -\beta \ln \left(\ln 2\right),$ и среднее значение определяется выражением

$\operatorname {E} (X)=\mu +\gamma \beta$,

где $\gamma$ – постоянная Эйлера–Машерони .

Стандартное отклонение $\sigma$ является $\beta \pi /{\sqrt {6}}$ следовательно $\beta =\sigma {\sqrt {6}}/\pi \approx 0.78\sigma .$

В режиме, где $x=\mu$, значение $F(x;\mu ,\beta )$ становится $e^{-1}\approx 0.37$, независимо от стоимости $\beta .$

Если $G_{1},...,G_{k}$ являются случайными величинами iid Gumbel с параметрами $(\mu ,\beta )$ затем $\max\{G_{1},...,G_{k}\}$ также является случайной величиной Гамбеля с параметрами $(\mu +\beta \ln k,\beta )$.

Если $G_{1},G_{2},...$ являются iid случайными величинами такими, что $\max\{G_{1},...,G_{k}\}-\beta \ln k$ имеет то же распределение, что и $G_{1}$ для всех натуральных чисел $k$, затем $G_{1}$ обязательно распределяется по Гамбелю с параметром масштаба $\beta$ (на самом деле достаточно рассмотреть только два различных значения k>1, которые взаимно просты).

Связанные дистрибутивы

• Если $X$ имеет распределение Гамбеля, то условное распределение Y = − X при условии, что Y положительное, или, что то же самое, при условии, что X отрицательное, имеет распределение Гомпертца . CDF G Y X связан с , cdf F , по формуле $G(y)=P(Y\leq y)=P(X\geq -y\mid X\leq 0)=(F(0)-F(-y))/F(0)$ при y > 0. Следовательно, плотности связаны соотношением $g(y)=f(-y)/F(0)$: плотность Гомпертца пропорциональна отраженной плотности Гамбеля, ограниченной положительной полуосью.
• Если X — экспоненциально распределенная переменная со средним значением 1, то −log( X ) имеет стандартное распределение Гамбеля.
• Если $X\sim \mathrm {Gumbel} (\alpha _{X},\beta )$ и $Y\sim \mathrm {Gumbel} (\alpha _{Y},\beta )$ независимы, то $X-Y\sim \mathrm {Logistic} (\alpha _{X}-\alpha _{Y},\beta )\,$ (см. Логистическое распределение ).
• Если $X,Y\sim \mathrm {Gumbel} (\alpha ,\beta )$ независимы, то $X+Y\nsim \mathrm {Logistic} (2\alpha ,\beta )$. Обратите внимание, что $E(X+Y)=2\alpha +2\beta \gamma \neq 2\alpha =E\left(\mathrm {Logistic} (2\alpha ,\beta )\right)$. В более общем смысле, распределение линейных комбинаций независимых случайных величин Гамбеля может быть аппроксимировано распределениями GNIG и GIG.

Теория, связанная с обобщенным многомерным лог-гамма-распределением, представляет собой многомерную версию распределения Гамбеля.

Возникновение и применение

Распределение соответствует доверительному интервалу кумулятивного распределения Гамбеля для максимального количества осадков за один день в октябре.

Гамбел показал, что максимальное значение (или статистика последнего порядка ) в выборке случайных величин, следующих экспоненциальному распределению, минус натуральный логарифм размера выборки. приближается к распределению Гамбеля по мере увеличения размера выборки.

Конкретно, пусть $\rho (x)=e^{-x}$ быть распределением вероятностей $x$ и $Q(x)=1-e^{-x}$ его кумулятивное распределение. Тогда максимальное значение из $N$ реализации $x$ меньше, чем $X$ тогда и только тогда, когда все реализации меньше, чем $X$. Таким образом, совокупное распределение максимального значения ${\tilde {x}}$ удовлетворяет

$P({\tilde {x}}-\log(N)\leq X)=P({\tilde {x}}\leq X+\log(N))=[Q(X+\log(N))]^{N}=\left(1-{\frac {e^{-X}}{N}}\right)^{N},$

и, по большому счету $N$, правая часть сходится к $e^{-e^{(-X)}}.$

Поэтому в гидрологии распределение Гумбеля используется для анализа таких переменных, как месячные и годовые максимальные значения суточного количества осадков и объемы речного стока, а также для описания засух.

Гамбель также показал, что оценка r ⁄ ( n +1) для вероятности события — где r — ранг наблюдаемого значения в ряду данных, а — общее количество наблюдений — является несмещенной оценкой кумулятивной вероятности вокруг режима n распределение. Поэтому эта оценка часто используется в качестве позиции для построения графика .

В теории чисел распределение Гамбеля аппроксимирует количество членов в случайном разделе целого числа. а также скорректированные по тренду размеры максимальных промежутков между простыми созвездиями и максимальных промежутков между простыми созвездиями .

Это появляется в задаче сборщика купонов .

Трюки с репараметризацией Gumbel

В машинном обучении распределение Гамбеля иногда используется для создания выборок из категориального распределения . Этот метод называется «трюком Гамбел-макса» и представляет собой особый пример « трюков репараметризации ».

Подробно, пусть $(\pi _{1},\ldots ,\pi _{n})$ неотрицательны и не все равны нулю, и пусть $g_{1},\ldots ,g_{n}$ быть независимыми выборками Gumbel(0, 1), затем путем обычного интегрирования $$Pr(j=\arg \max _{i}(g_{i}+\log \pi _{i}))={\frac {\pi _{j}}{\sum _{i}\pi _{i}}}$$То есть, $\arg \max _{i}(g_{i}+\log \pi _{i})\sim {\text{Categorical}}\left({\frac {\pi _{j}}{\sum _{i}\pi _{i}}}\right)_{j}$

Эквивалентно, учитывая любой $x_{1},...,x_{n}\in \mathbb {R}$, мы можем выполнить выборку из распределения Больцмана по формуле

$$Pr(j=\arg \max _{i}(g_{i}+x_{i}))={\frac {e^{x_{j}}}{\sum _{i}e^{x_{i}}}}$$Связанные уравнения включают:

• Если $x\sim \operatorname {Exp} (\lambda )$, затем $(-\ln x-\gamma )\sim {\text{Gumbel}}(-\gamma +\ln \lambda ,1)$.
• $\arg \max _{i}(g_{i}+\log \pi _{i})\sim {\text{Categorical}}\left({\frac {\pi _{j}}{\sum _{i}\pi _{i}}}\right)_{j}$.
• $\max _{i}(g_{i}+\log \pi _{i})\sim {\text{Gumbel}}\left(\log \left(\sum _{i}\pi _{i}\right),1\right)$. То есть дистрибутив Гамбеля представляет собой максимально стабильное семейство дистрибутивов.
• $\mathbb {E} [\max _{i}(g_{i}+\beta x_{i})]=\log \left(\sum _{i}e^{\beta x_{i}}\right)+\gamma .$

Генерация случайной переменной

Дополнительная информация: Генерация неоднородных случайных величин.

Поскольку функция квантиля (обратная кумулятивная функция распределения ), $Q(p)$, распределения Гамбеля определяется выражением

$Q(p)=\mu -\beta \ln(-\ln(p)),$

вариант $Q(U)$ имеет распределение Гамбеля с параметрами $\mu$ и $\beta$ когда случайная величина $U$ извлекается из равномерного распределения на интервале $(0,1)$.

Вероятностная бумага

Кусок миллиметровой бумаги, включающий распределение Гамбеля.

Во времена, когда еще не было программного обеспечения, для изображения распределения Гамбеля использовалась вероятностная бумага (см. Иллюстрацию). Работа основана на линеаризации кумулятивной функции распределения. $F$ :

$-\ln[-\ln(F)]={\frac {x-\mu }{\beta }}$

В статье горизонтальная ось построена в двойном логарифмическом масштабе. Вертикальная ось линейна. Построив график $F$ на горизонтальной оси бумаги и $x$-переменная по вертикальной оси, распределение представлено прямой линией с наклоном 1 $/\beta$. Когда для определения распределения, стало доступно программное обеспечение такое как CumFreq , задача построения графика распределения стала проще.

См. также

• Распространение гумбеля типа 2
• Теория экстремальных ценностей
• Обобщенное распределение экстремальных значений
• Теорема Фишера – Типпета – Гнеденко.
• Эмиль Юлиус Гумбель