Премьер-разрыв

простых чисел Распределение частот для простых чисел до 1,6 миллиарда. Пики возникают при кратности 6.

Промежуток между простыми числами — это разница между двумя последовательными простыми числами . n - й простой пробел, обозначаемый gn _n или g ( pn ₎ , представляет собой разность между ( т.е. + 1)-м и n -м простыми числами,

$g_{n}=p_{n+1}-p_{n}.\$

Имеем g ₁ = 1, g ₂ = g ₃ = 2 и g ₄ = 4. Последовательность ( g _n ) простых пробелов тщательно изучена; однако многие вопросы и предположения остаются без ответа.

Первые 60 простых пробелов:

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ... (последовательность A001223 в OEIS ).

По определению g _n каждое простое число можно записать как

$p_{n+1}=2+\sum _{i=1}^{n}g_{i}.$

Простые наблюдения

Первый, наименьший и единственный нечетный простой пробел — это разрыв размером 1 между 2, единственным четным простым числом, и 3, первым нечетным простым числом. Все остальные простые промежутки четные. Существует только одна пара последовательных пробелов длиной 2: пробелы g2 _. и g3 ₇ между простыми числами 3, 5 и

Для любого числа n факториал n ! целого является произведением всех положительных целых чисел до n включительно . Тогда в последовательности

$n!+2,\;n!+3,\;\ldots ,\;n!+n$

первое слагаемое делится на 2, второе слагаемое делится на 3 и так далее. Таким образом, это последовательность из n - 1 последовательных составных целых чисел, и она должна принадлежать промежутку между простыми числами, имеющими длину не менее n . числами есть сколь угодно большие промежутки, то есть для любого целого числа N существует целое число m с g _m ≥ N. Отсюда следует, что между простыми

Однако пробелы между простыми числами из n чисел могут возникать и в числах, намного меньших, чем n !. Например, первый пробел между простыми числами размером больше 14 возникает между простыми числами 523 и 541, а 15! это гораздо большее число 1307674368000.

Средний разрыв между простыми числами увеличивается пропорционально натуральному логарифму этих простых чисел, и, следовательно, отношение разрыва между простыми числами к участвующим простым числам уменьшается (и асимптотически равно нулю). Это следствие теоремы о простых числах . С эвристической точки зрения мы ожидаем, что вероятность того, что отношение длины промежутка к натуральному логарифму больше или равно фиксированному положительному числу k, будет равна e ^{- к} ; следовательно, отношение может быть сколь угодно большим. Действительно, отношение пробела к количеству цифр задействованных целых чисел действительно неограниченно увеличивается. Это следствие результата Вестзинтиуса.

В противоположном направлении гипотеза о простых числах-близнецах утверждает, что g _n = 2 для бесконечного числа целых чисел n .

Численные результаты

Обычно соотношение ${\textstyle {\frac {g_{n}}{\ln(p_{n})}}}$ называется достоинством зазора g _n . Неформально, достоинство пробела g _n можно рассматривать как отношение размера пробела к средним размерам простого пробела в окрестности p _n .

Самый большой из известных пробелов в простых числах с идентифицированными вероятными концами пробелов в простых числах имеет длину 16 045 848, с 385 713-значными вероятными простыми числами и достоинством M = 18,067, найденный Андреасом Хёглундом в марте 2024 года. Самый большой известный пробел между простыми числами с идентифицированными проверенными простыми числами на концах пробела имеет длину 1 113 106 и ценность 25,90, при этом 18 662-значные простые числа были найдены П. Ками, М. Янсеном и Дж. К. Андерсеном.

По состоянию на сентябрь 2022 г. , самое большое известное значение качества и первое значение с достоинством более 40, как обнаружила сеть Gapcoin , составляет 41,93878373 с 87-значным простым числом 2 9 3 7 0 3 2 3 4 0 6 8 0 2 2 5 9 0 1 5 8 7 2 3 7 6 6 1 0 4 4 1 9 4 6 3 4 2 5 7 0 9 0 7 5 5 7 4 8 1 1 7 6 2 0 9 8 5 8 8 7 9 8 2 1 7 8 9 5 7 2 8 8 5 8 6 7 6 7 2 8 1 4 3 2 2 7. Разница между этим простым числом и следующим простым числом равна 8350.

Наибольшие известные значения достоинств (по состоянию на октябрь 2020 г.) )

Заслуга	г н	цифры	п н	Дата	Первооткрыватель
41.938784	0 8350	00 87	см. выше	2017	Гапкоин
39.620154	15900	0 175	3483347771 × 409 # / 00 30 − 7016	2017	Дана Якобсен
38.066960	18306	0 209	0 650094367 × 491#/2310 − 8936	2017	Дана Якобсен
38.047893	35308	0 404	0 100054841 × 953#/ 0 210 − 9670	2020	Сет Троизи
37.824126	0 8382	00 97	0 512950801 × 229#/5610 − 4138	2018	Дана Якобсен

Отношение Крамера-Шенкса-Гранвилля представляет собой отношение g _n / (ln( p _n )) ² . Если отбросить аномально высокие значения отношения для простых чисел 2, 3, 7, то наибольшее известное значение этого отношения составляет 0,9206386 для простого числа 1693182318746371. Другие рекордные термины можно найти на сайте OEIS : A111943 .

Мы говорим, что g _n является максимальным разрывом , если g _m < g _n для всех m < n . По состоянию на май 2024 г. , самый большой известный максимальный пробел между простыми числами имеет длину 1572, найденный Крейгом Лойзидесом. Это 82-й максимальный разрыв между простыми числами, и он происходит после простого числа 18571673432051830099. Другие рекордные (максимальные) размеры разрыва можно найти в OEIS : A005250 , с соответствующими простыми числами p _n в OEIS : A002386 и значениями n в OEIS : A005669 . последовательность максимальных пробелов до n- го простого числа имеет около Предполагается, что $2\ln n$ условия (см. таблицу ниже).

82 известных максимальных пробела в простых числах

Номера от 1 до 27 # г н п н н 1 1 2 1 2 2 3 2 3 4 7 4 4 6 23 9 5 8 89 24 6 14 113 30 7 18 523 99 8 20 887 154 9 22 1,129 189 10 34 1,327 217 11 36 9,551 1,183 12 44 15,683 1,831 13 52 19,609 2,225 14 72 31,397 3,385 15 86 155,921 14,357 16 96 360,653 30,802 17 112 370,261 31,545 18 114 492,113 40,933 19 118 1,349,533 103,520 20 132 1,357,201 104,071 21 148 2,010,733 149,689 22 154 4,652,353 325,852 23 180 17,051,707 1,094,421 24 210 20,831,323 1,319,945 25 220 47,326,693 2,850,174 26 222 122,164,747 6,957,876 27 234 189,695,659 10,539,432

Номера с 28 по 54 # г н п н н 28 248 191,912,783 10,655,462 29 250 387,096,133 20,684,332 30 282 436,273,009 23,163,298 31 288 1,294,268,491 64,955,634 32 292 1,453,168,141 72,507,380 33 320 2,300,942,549 112,228,683 34 336 3,842,610,773 182,837,804 35 354 4,302,407,359 203,615,628 36 382 10,726,904,659 486,570,087 37 384 20,678,048,297 910,774,004 38 394 22,367,084,959 981,765,347 39 456 25,056,082,087 1,094,330,259 40 464 42,652,618,343 1,820,471,368 41 468 127,976,334,671 5,217,031,687 42 474 182,226,896,239 7,322,882,472 43 486 241,160,624,143 9,583,057,667 44 490 297,501,075,799 11,723,859,927 45 500 303,371,455,241 11,945,986,786 46 514 304,599,508,537 11,992,433,550 47 516 416,608,695,821 16,202,238,656 48 532 461,690,510,011 17,883,926,781 49 534 614,487,453,523 23,541,455,083 50 540 738,832,927,927 28,106,444,830 51 582 1,346,294,310,749 50,070,452,577 52 588 1,408,695,493,609 52,302,956,123 53 602 1,968,188,556,461 72,178,455,400 54 652 2,614,941,710,599 94,906,079,600

Номера с 55 по 82 # г н п н н 55 674 7,177,162,611,713 251,265,078,335 56 716 13,829,048,559,701 473,258,870,471 57 766 19,581,334,192,423 662,221,289,043 58 778 42,842,283,925,351 1,411,461,642,343 59 804 90,874,329,411,493 2,921,439,731,020 60 806 171,231,342,420,521 5,394,763,455,325 61 906 218,209,405,436,543 6,822,667,965,940 62 916 1,189,459,969,825,483 35,315,870,460,455 63 924 1,686,994,940,955,803 49,573,167,413,483 64 1,132 1,693,182,318,746,371 49,749,629,143,526 65 1,184 43,841,547,845,541,059 1,175,661,926,421,598 66 1,198 55,350,776,431,903,243 1,475,067,052,906,945 67 1,220 80,873,624,627,234,849 2,133,658,100,875,638 68 1,224 203,986,478,517,455,989 5,253,374,014,230,870 69 1,248 218,034,721,194,214,273 5,605,544,222,945,291 70 1,272 305,405,826,521,087,869 7,784,313,111,002,702 71 1,328 352,521,223,451,364,323 8,952,449,214,971,382 72 1,356 401,429,925,999,153,707 10,160,960,128,667,332 73 1,370 418,032,645,936,712,127 10,570,355,884,548,334 74 1,442 804,212,830,686,677,669 20,004,097,201,301,079 75 1,476 1,425,172,824,437,699,411 34,952,141,021,660,495 76 1,488 5,733,241,593,241,196,731 135,962,332,505,694,894 77 1,510 6,787,988,999,657,777,797 160,332,893,561,542,066 78 1,526 15,570,628,755,536,096,243 360,701,908,268,316,580 79 1,530 17,678,654,157,568,189,057 408,333,670,434,942,092 80 1,550 18,361,375,334,787,046,697 423,731,791,997,205,041 81 1,552 18,470,057,946,260,698,231 426,181,820,436,140,029 82 1,572 18,571,673,432,051,830,099 428,472,240,920,394,477

Дальнейшие результаты

Верхние границы

Постулат Бертрана , доказанный всегда есть простое число в 1852 году, гласит, что между k и 2 k , поэтому, в частности, p _{n +1} < 2 p _n , что означает g _n < p _n .

Теорема о простых числах , доказанная в 1896 году, гласит, что средняя длина промежутка между простым числом p и следующим простым числом будет асимптотически приближаться к ln( p ), натуральному логарифму числа p , для достаточно больших простых чисел. Фактическая длина зазора может быть намного больше или меньше этой. Однако из теоремы о простых числах можно вывести верхнюю оценку длины пробелов в простых числах:

Для каждого $\epsilon >0$, есть номер $N$ такой, что для всех $n>N$

$g_{n}<p_{n}\epsilon$.

Можно также сделать вывод, что промежутки становятся сколь угодно меньшими пропорционально простым числам: частное

$\lim _{n\to \infty }{\frac {g_{n}}{p_{n}}}=0.$

Хохайзель (1930) был первым, кто показал что существует константа θ < 1 такая, что

$\pi (x+x^{\theta })-\pi (x)\sim {\frac {x^{\theta }}{\log(x)}}{\text{ as }}x\to \infty ,$

следовательно, показывая, что

$g_{n}<p_{n}^{\theta },\,$

для достаточно большого   n .

Хохайзель получил возможное значение 32999/33000 для θ . улучшил это значение до 249/250 Хайльбронн . и θ = 3/4 + ε для любого ε > 0 — по Чудакову .

Значительное улучшение произошло благодаря Ингхэму . который показал, что для некоторой положительной константы c ,

если $\zeta (1/2+it)=O(t^{c})$ затем $\pi (x+x^{\theta })-\pi (x)\sim {\frac {x^{\theta }}{\log(x)}}$ для любого $\theta >(1+4c)/(2+4c).$

Здесь O относится к большому обозначению O , ζ обозначает дзета-функцию Римана , а π — функцию подсчета простых чисел . Зная, что любое c > 1/6 допустимо, получаем, что θ может быть любым числом, большим 5/8.

Непосредственным следствием результата Ингэма является то, что между n и n всегда существует простое число. ³ и ( п + 1) ³ , если n достаточно велико. Гипотеза Линделёфа подразумевала бы, что формула Ингема справедлива для c любого положительного числа: но даже этого было бы недостаточно, чтобы предположить, что между n и существует простое число. ² и ( п + 1) ² при достаточно большом n (см. гипотезу Лежандра ). более сильный результат, такой как гипотеза Крамера Чтобы проверить это, потребуется .

Хаксли в 1972 году показал, что можно выбрать θ = 7/12 = 0,58(3).

Результат, полученный Бейкером, Харманом и Пинцем в 2001 году, показывает, что θ можно принять равным 0,525.

В 2005 году Дэниел Голдстон , Янош Пинц и Джем Йылдырым доказали, что

$\liminf _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=0$

и через 2 года улучшил это к

$\liminf _{n\to \infty }{\frac {g_{n}}{{\sqrt {\log p_{n}}}(\log \log p_{n})^{2}}}<\infty .$

В 2013 году Итан Чжан доказал, что

$\liminf _{n\to \infty }g_{n}<7\cdot 10^{7},$

это означает, что существует бесконечно много пробелов, не превышающих 70 миллионов. Совместными усилиями проекта Polymath Project по оптимизации границы Чжана удалось снизить ее до 4680 20 июля 2013 года. В ноябре 2013 года Джеймс Мейнард представил новое уточнение решета GPY , позволяющее ему уменьшить оценку до 600 и показать, что для любого m существует ограниченный интервал с бесконечным количеством переводов, каждый из которых содержит m простых чисел. Используя идеи Мейнарда, проект Polymath улучшил оценку до 246; предполагая гипотезу Эллиотта – Хальберштама и ее обобщенную форму , оценка была уменьшена до 12 и 6 соответственно.

Нижние границы

В 1931 году Эрик Вестзинтиус доказал, что максимальные пробелы в простых числах растут более чем логарифмически. То есть,

$\limsup _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=\infty .$

В 1938 году Роберт Рэнкин доказал существование константы c > 0 такой, что неравенство

$g_{n}>{\frac {c\ \log n\ \log \log n\ \log \log \log \log n}{(\log \log \log n)^{2}}}$

справедливо для бесконечно многих значений n , улучшая результаты Вестзинтиуса и Пауля Эрдеша . Позже он показал, что можно взять любую константу c < e ^с , где γ — постоянная Эйлера–Машерони . Значение константы c было улучшено в 1997 году до любого значения меньше 2 e. ^с .

Пол Эрдеш предложил премию в 10 000 долларов за доказательство или опровержение того, что константу c в приведенном выше неравенстве можно считать сколь угодно большой. Это подтвердили в 2014 году Форд-Грин-Конягин-Тао и независимо Джеймс Мейнард.

Результат был дополнительно улучшен до

$g_{n}>{\frac {c\ \log n\ \log \log n\ \log \log \log \log n}{\log \log \log n}}$

для бесконечно многих значений n по Форду–Грину–Конягину–Мейнарду–Тао.

В духе первоначальной премии Эрдеша Теренс Тао предложил 10 000 долларов США за доказательство того, что в этом неравенстве c можно взять сколь угодно большим.

Также были определены нижние оценки для цепочек простых чисел.

Гипотезы о промежутках между простыми числами

Функция простого разрыва

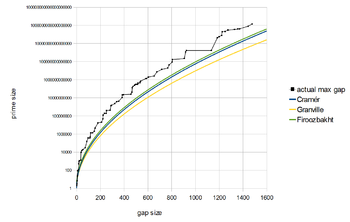
Еще лучшие результаты возможны в рамках гипотезы Римана . Харальд Крамер доказал что из гипотезы Римана следует, что разрыв g _n удовлетворяет

$g_{n}=O({\sqrt {p_{n}}}\log p_{n}),$

используя большое обозначение О. (На самом деле для этого результата требуется только более слабая гипотеза Линделёфа , если можно допустить бесконечно больший показатель степени. )Позже он предположил, что разрывы еще меньше. Грубо говоря, гипотеза Крамера утверждает, что

$g_{n}=O\!\left((\log p_{n})^{2}\right)\!.$

Гипотеза Фирозбахта утверждает, что $p_{n}^{1/n}\!$ (где $p_{n}$ — n- е простое число) является строго убывающей функцией от n , т. е.

$p_{n+1}^{1/(n+1)}\!<p_{n}^{1/n}{\text{ for all }}n\geq 1.$

Если эта гипотеза верна, то функция $g_{n}=p_{n+1}-p_{n}$ удовлетворяет $g_{n}<(\log p_{n})^{2}-\log p_{n}{\text{ for all }}n>4.$ Это подразумевает сильную форму гипотезы Крамера, но несовместимо с эвристикой Гранвилля и Пинца. которые предполагают, что $g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}$ бесконечно часто для любого $\varepsilon >0,$ где $\gamma$ обозначает константу Эйлера–Машерони .

Между тем гипотеза Оппермана слабее гипотезы Крамера. Ожидаемый размер разрыва с гипотезой Оппермана составляет порядка

$g_{n}<{\sqrt {p_{n}}}.$

В результате по гипотезе Оппермана существует $m$ (вероятно $m=30$), для которого каждое натуральное число $n>m$ удовлетворяет $g_{n}<{\sqrt {p_{n}}}.$

Гипотеза Андрики , которая является более слабой, чем гипотеза Оппермана, утверждает, что

$g_{n}<2{\sqrt {p_{n}}}+1.$

Это небольшое усиление гипотезы Лежандра о том, что между последовательными квадратными числами всегда находится простое число.

Гипотеза Полиньяка утверждает, что каждое положительное четное число k бесконечно часто встречается как простое число. Случай k = 2 представляет собой гипотезу о простых числах-близнецах . Гипотеза еще не была доказана или опровергнута для какого-либо конкретного значения k , но обсуждавшиеся выше улучшения результата Чжана доказывают, что она верна по крайней мере для одного (на данный момент неизвестного) значения k ≤ 246.

Как арифметическая функция

Промежуток g _n между n -м и ( n + 1)-м простыми числами является примером арифметической функции . В этом контексте ее обычно обозначают d _n и называют функцией простой разности. Функция не является ни мультипликативной , ни аддитивной .

См. также

• Неравенство Бонса
• Гауссов ров
• Твин Прайм

Ссылки

• Гай, Ричард К. (2004). Нерешенные проблемы теории чисел (3-е изд.). Спрингер-Верлаг . ISBN  978-0-387-20860-2 . Збл   1058.11001 .

Дальнейшее чтение

• Саундарараджан, Каннан (2007). «Малые промежутки между простыми числами: работа Голдстона-Пинца-Йылдырыма». Бык. Являюсь. Математика. Соц . Новая серия. 44 (1): 1–18. arXiv : math/0605696 . дои : 10.1090/s0273-0979-06-01142-6 . S2CID   119611838 . Збл   1193.11086 .
• Михайлеску, Преда (июнь 2014 г.). «О некоторых гипотезах аддитивной теории чисел» (PDF) . Информационный бюллетень EMS (92): 13–16. дои : 10.4171/НОВОСТИ . hdl : 2117/17085 . ISSN   1027-488X .

Внешние ссылки

• Томас Р. Найсли , Некоторые результаты вычислительных исследований простых чисел - Вычислительная теория чисел . Этот справочный веб-сайт включает список всех первых известных пробелов в простых числах.
• Вайсштейн, Эрик В. «Функция простой разности» . Математический мир .
• «Функция простой разности» . ПланетаМатематика .
• Армин Шамс, расширяя теорему Чебышева о гипотезе Бертрана , не предполагает «произвольно большой» константы, как некоторые другие результаты.
• Крис Колдуэлл , Промежутки между простыми числами ; элементарное введение
• Эндрю Гранвилл , Простые числа в интервалах ограниченной длины ; обзор результатов, полученных на данный момент, вплоть до работы Джеймса Мейнарда в ноябре 2013 года.