Функция подсчета простых чисел

В этой статье используются технические математические обозначения логарифмов. Все экземпляры log( x ) без индексной базы следует интерпретировать как натуральный логарифм , обычно обозначаемый как ln( x ) или log _e ( x ).

В математике функция подсчета простых чисел — это функция , подсчитывающая количество простых чисел, меньших или равных некоторому действительному числу $x$ . ^[1]^[2] Он обозначается $π (x)$ (не связан с числом $π$ ).

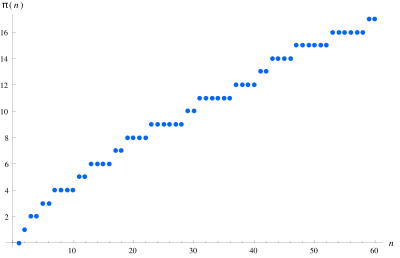
Значения $π (n)$ для первых 60 положительных целых чисел

Темпы роста [ править ]

Большой интерес в теории чисел представляет скорость роста функции подсчета простых чисел. ^[3]^[4] , что оно предположили В конце XVIII века Гаусс и Лежандр составляет примерно

{\frac {x}{\log(x)}}

где

log

— натуральный логарифм в том смысле, что

\lim _{x\rightarrow \infty }{\frac {\pi (x)}{x/\log(x)}}=1.

Это утверждение является теоремой о простых числах . Эквивалентное утверждение

\lim _{x\rightarrow \infty }{\frac {\pi (x)}{\operatorname {li} (x)}}=1

где

li

— логарифмическая интегральная функция. Теорема о простых числах была впервые доказана в 1896 году Жаком Адамаром и Шарлем де ла Валле Пуссеном независимо друг от друга с использованием свойств дзета-функции Римана , введенной Риманом доказательства теоремы о простых числах без использования дзета-функции или комплексного анализа в 1859 году. Были найдены . около 1948 года Атле Сельберг и Пол Эрдеш (по большей части независимо). ^[5]

точные оценки Более

В 1899 году де ла Валле Пуссен доказал, что ^[6]

\pi (x)=\operatorname {li} (x)+O\left(xe^{-a{\sqrt {\log x}}}\right)\quad {\text{as }}x\to \infty

для некоторой положительной константы

a

. Здесь

O (...)

— большое

O.

обозначение это

более точные оценки $π (x)$ Теперь известны . Например, в 2002 году Кевин Форд доказал, что ^[7]

\pi (x)=\operatorname {li} (x)+O\left(x\exp \left(-0.2098(\log x)^{3/5}(\log \log x)^{-1/5}\right)\right).

Мосингхофф и Труджиан доказали ^[8] явная верхняя граница разницы между $π (x)$ и $li(x)$ :

{\bigl |}\pi (x)-\operatorname {li} (x){\bigr |}\leq 0.2593{\frac {x}{(\log x)^{3/4}}}\exp \left(-{\sqrt {\frac {\log x}{6.315}}}\right)\quad {\text{for }}x\geq 229.

Для значений $x$ , которые не являются неоправданно большими, $li(x)$ больше $π (x)$ . Однако $, что π (x) - li(x)$ известно меняет знак бесконечное число раз. Обсуждение этого вопроса см. в номере Скьюза .

Точная форма [ править ]

Для $x > 1$ пусть $π 0 ( x ) = π ( x ) − .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/2 , — простое$ когда $x$ число, и $π 0 (x) = π (x)$ в противном случае. Бернхард Риман в своей работе « О числе простых чисел, меньших заданной величины» доказал, $π0 что (x)$ равно ^[9]

\pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho }),

где

\operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} \left(x^{1/n}\right),

µ (n)

— функция Мёбиуса ,

li(x)

— логарифмическая интегральная функция ,

ρ

индексирует каждый нуль дзета-функции Римана и

li(x р / н)

не оценивается с разрезом ветки , а вместо этого рассматривается как

Ei(ρ / n log x)

, где

Ei(x)

— экспоненциальный интеграл . Если собрать тривиальные нули и суммировать только по нетривиальным нулям

ρ

дзета-функции Римана, то

π 0 (x)

можно аппроксимировать выражением ^[10]

\pi _{0}(x)\approx \operatorname {R} (x)-\sum _{\rho }\operatorname {R} \left(x^{\rho }\right)-{\frac {1}{\log(x)}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\log(x)}}.

Гипотеза Римана предполагает, что каждый такой нетривиальный нуль лежит вдоль $Re(s) = 1 / 2$ .

Таблица $π (x)$ , $x / log(x)$ и $li(x)$ [ редактировать ]

В таблице сравниваются точные значения $π (x)$ с двумя приближениями $x / log x$ и $li (x)$ . Последний столбец, $x / π (x)$ , представляет собой средний разрыв простых чисел ниже $x$ .

$Икс$	$π (Икс)$	$π (Икс) - х / журнал(х)$	$li(Икс) - π (Икс)$	$х / журнал(х)$ % ошибка	$ли (х)$ % ошибка	$Икс / π (Икс)$
10	4	0	2	8.22%	42.606%	2.500
10 ²	25	3	5	14.06%	18.597%	4.000
10 ³	168	23	10	14.85%	5.561%	5.952
10 ⁴	1,229	143	17	12.37%	1.384%	8.137
10 ⁵	9,592	906	38	9.91%	0.393%	10.425
10 ⁶	78,498	6,116	130	8.11%	0.164%	12.739
10 ⁷	664,579	44,158	339	6.87%	0.051%	15.047
10 ⁸	5,761,455	332,774	754	5.94%	0.013%	17.357
10 ⁹	50,847,534	2,592,592	1,701	5.23%	3.34 × 10 ⁻³ %	19.667
10 ¹⁰	455,052,511	20,758,029	3,104	4.66%	6.82 × 10 ⁻⁴ %	21.975
10 ¹¹	4,118,054,813	169,923,159	11,588	4.21%	2.81 × 10 ⁻⁴ %	24.283
10 ¹²	37,607,912,018	1,416,705,193	38,263	3.83%	1.02 × 10 ⁻⁴ %	26.590
10 ¹³	346,065,536,839	11,992,858,452	108,971	3.52%	3.14 × 10 ⁻⁵ %	28.896
10 ¹⁴	3,204,941,750,802	102,838,308,636	314,890	3.26%	9.82 × 10 ⁻⁶ %	31.202
10 ¹⁵	29,844,570,422,669	891,604,962,452	1,052,619	3.03%	3.52 × 10 ⁻⁶ %	33.507
10 ¹⁶	279,238,341,033,925	7,804,289,844,393	3,214,632	2.83%	1.15 × 10 ⁻⁶ %	35.812
10 ¹⁷	2,623,557,157,654,233	68,883,734,693,928	7,956,589	2.66%	3.03 × 10 ⁻⁷ %	38.116
10 ¹⁸	24,739,954,287,740,860	612,483,070,893,536	21,949,555	2.51%	8.87 × 10 ⁻⁸ %	40.420
10 ¹⁹	234,057,667,276,344,607	5,481,624,169,369,961	99,877,775	2.36%	4.26 × 10 ⁻⁸ %	42.725
10 ²⁰	2,220,819,602,560,918,840	49,347,193,044,659,702	222,744,644	2.24%	1.01 × 10 ⁻⁸ %	45.028
10 ²¹	21,127,269,486,018,731,928	446,579,871,578,168,707	597,394,254	2.13%	2.82 × 10 ⁻⁹ %	47.332
10 ²²	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1,932,355,208	2.03%	9.59 × 10 ⁻¹⁰ %	49.636
10 ²³	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	7,250,186,216	1.94%	3.76 × 10 ⁻¹⁰ %	51.939
10 ²⁴	18,435,599,767,349,200,867,866	339,996,354,713,708,049,069	17,146,907,278	1.86%	9.31 × 10 ⁻¹¹ %	54.243
10 ²⁵	176,846,309,399,143,769,411,680	3,128,516,637,843,038,351,228	55,160,980,939	1.78%	3.21 × 10 ⁻¹¹ %	56.546
10 ²⁶	1,699,246,750,872,437,141,327,603	28,883,358,936,853,188,823,261	155,891,678,121	1.71%	9.17 × 10 ⁻¹² %	58.850
10 ²⁷	16,352,460,426,841,680,446,427,399	267,479,615,610,131,274,163,365	508,666,658,006	1.64%	3.11 × 10 ⁻¹² %	61.153
10 ²⁸	157,589,269,275,973,410,412,739,598	2,484,097,167,669,186,251,622,127	1,427,745,660,374	1.58%	9.05 × 10 ⁻¹³ %	63.456
10 ²⁹	1,520,698,109,714,272,166,094,258,063	23,130,930,737,541,725,917,951,446	4,551,193,622,464	1.53%	2.99 × 10 ⁻¹³ %	65.759

В Электронной энциклопедии целочисленных последовательностей столбец π $— (x)$ это последовательность OEIS : A006880 , $π (x) - x / log x$ — это последовательность OEIS : A057835 , а $li(x) - π (x)$ — это последовательность OEIS : A057752 .

Значение $π (10 24)$ первоначально была вычислена Дж. Бюте, Дж. Франке , А. Йостом и Т. Кляйнъунгом в предположении гипотезы Римана . ^[11] Позже это было безоговорочно подтверждено расчетами DJ Platt. ^[12] Значение $π (10 25)$ принадлежит Й. Бюте, Й. Франке , А. Йосту и Т. Кляйнъюнгу. ^[13] Значение $π (10 26)$ было рассчитано DB Staple. ^[14] Все остальные предыдущие записи в этой таблице также были проверены в рамках этой работы.

Значения для 10 ²⁷, 10 ²⁸, и 10 ²⁹ были объявлены Дэвидом Боугом и Ким Валишем в 2015 году, ^[15] 2020, ^[16] и 2022 год, ^[17] соответственно.

Алгоритмы вычисления $π (x)$ [ править ]

Простой способ найти $π (x)$ , если $x$ не слишком велик, — это использовать решето Эратосфена, чтобы получить простые числа, меньшие или равные $x$ , а затем посчитать их.

Более сложный способ нахождения $π (x)$ принадлежит Лежандру (с использованием принципа включения-исключения : при заданном $x$ , если $p1,) p2 различные простые,\dots, pn —$ числа, то количество целых чисел меньше или равный $x$ , который не делится ни на один $p i$ ,

\lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots

(где $⌊ x ⌋$ обозначает функцию пола ). Следовательно, это число равно

\pi (x)-\pi \left({\sqrt {x}}\right)+1

когда числа $p 1, p 2,\dots, p n$ являются простыми числами, меньшими или равными квадратному корню из $x$ .

Алгоритм Мейселя-Лемера [ править ]

В серии статей, опубликованных между 1870 и 1885 годами, Эрнст Мейсель описал (и использовал) практический комбинаторный способ вычисления $π (x)$ : пусть $p 1, p 2,\dots, p n$ — первые $n$ простых чисел и обозначают $Φ(m, n)$ количество натуральных чисел не больше $m$ , которые не делятся ни на одно из чисел $для pi$ любого $i \leq n$ . Затем

\Phi (m,n)=\Phi (m,n-1)-\Phi \left({\frac {m}{p_{n}}},n-1\right).

Учитывая натуральное число $m$ , если $n = π (3 \sqrt м),$ и если $µ знак равно π (\sqrt м) - п$ , то

\pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right).

Используя этот подход, Мейсель вычислил $π (x)$ для $x$ , равного 5 × 10 ⁵, 10 ⁶, 10 ⁷, и 10 ⁸.

В 1959 году Деррик Генри Лемер расширил и упростил метод Мейселя. Определите для действительных $m$ и натуральных чисел $n$ и $k$ m $P k (m, n)$ как количество чисел, не превышающих $,$ с ровно $k$ простыми делителями, все из которых больше $p n$ . Кроме того, установите $P 0 (m, n) = 1$ . Затем

\Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)

где сумма на самом деле имеет лишь конечное число ненулевых членов. Пусть $y$ обозначает целое число такое, что $3 \sqrt m \leq y \leq \sqrt m$ и положим $n знак равно π (y)$ . Тогда $п 1 (м, п) знак равно π (м) - п$ и $п k (м, п) = 0,$ когда $k \geq 3$ . Поэтому,

\pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)

Вычисление $P 2 (m, n)$ можно получить таким образом:

P_{2}(m,n)=\sum _{y<p\leq {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right)

где сумма ведется по простым числам.

С другой стороны, вычисление $Φ(m, n)$ может быть выполнено с использованием следующих правил:

$\Phi (m,0)=\lfloor m\rfloor$
$\Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)$

Используя свой метод и IBM 701 , Лемер смог вычислить правильное значение $π (10 9)$ и пропустил правильное значение $π (10 10)$ на 1. ^[18]

Дальнейшие усовершенствования этого метода были внесены Лагариасом, Миллером, Одлизко, Делеглизом и Риватом. ^[19]

подсчета простых чисел Другие функции

Используются и другие функции подсчета простых чисел, поскольку с ними удобнее работать.

Римана чисел Функция подсчета простых

Функция подсчета простых чисел Римана обычно обозначается как $Π 0 (x)$ или $J 0 (x)$ . Он имеет прыжки $1 / n$ в степенях простых чисел $p н$ и оно принимает значение на полпути между двумя сторонами на разрывах $π (x)$ . Эта дополнительная деталь используется, поскольку функция затем может быть определена с помощью обратного преобразования Меллина .

Формально мы можем определить $Π 0 (x)$ как

\Pi _{0}(x)={\frac {1}{2}}\left(\sum _{p^{n}<x}{\frac {1}{n}}+\sum _{p^{n}\leq x}{\frac {1}{n}}\right)\

где переменная $p$ в каждой сумме варьируется по всем простым числам в указанных пределах.

Мы также можем написать

\ \Pi _{0}(x)=\sum _{n=2}^{x}{\frac {\Lambda (n)}{\log n}}-{\frac {\Lambda (x)}{2\log x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}\left(x^{1/n}\right)

где $Λ$ — функция фон Мангольдта и

\pi _{0}(x)=\lim _{\varepsilon \to 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.

дает формула обращения Мёбиуса Тогда

\pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\ \Pi _{0}\left(x^{1/n}\right),

где $µ (n)$ – функция Мёбиуса .

Зная связь между логарифмом дзета-функции Римана и функцией фон Мангольдта $Λ$ , и используя формулу Перрона, имеем

\log \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,\mathrm {d} x

Функция Чебышева [ править ]

Функция Чебышева взвешивает простые числа или степени простых чисел $p н$ по $журналу (р)$ :

{\begin{aligned}\theta (x)&=\sum _{p\leq x}\log p\\\psi (x)&=\sum _{p^{n}\leq x}\log p=\sum _{n=1}^{\infty }\theta \left(x^{1/n}\right)=\sum _{n\leq x}\Lambda (n).\end{aligned}}

Для $x \geq 2$ , ^[20]

\vartheta (x)=\pi (x)\log x-\int _{2}^{x}{\frac {\pi (t)}{t}}\,\mathrm {d} t

и

\pi (x)={\frac {\vartheta (x)}{\log x}}+\int _{2}^{x}{\frac {\vartheta (t)}{t\log ^{2}(t)}}\mathrm {d} t.

Формулы для функций подсчета простых чисел [ править ]

Формулы для функций, считающих простые числа, бывают двух видов: арифметические формулы и аналитические формулы. Аналитические формулы для подсчета простых чисел были первыми, использованными для доказательства теоремы о простых числах . Они происходят из работ Римана и фон Мангольдта и обычно известны как явные формулы . ^[21]

Имеем следующее выражение для второй функции Чебышева $ψ$ :

\psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\log 2\pi -{\frac {1}{2}}\log \left(1-x^{-2}\right),

где

\psi _{0}(x)=\lim _{\varepsilon \to 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.

Здесь $ρ$ — нули дзета-функции Римана в критической полосе, где действительная часть $ρ$ находится между нулем и единицей. Формула действительна для значений $x$ больше единицы, что является областью интереса. Сумма по корням условно сходится, и ее следует брать в порядке возрастания абсолютного значения мнимой части. Обратите внимание, что та же самая сумма по тривиальным корням дает последнее вычитаемое в формуле.

Для $Π 0 (x)$ имеем более сложную формулу

\Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} \left(x^{\rho }\right)-\log 2+\int _{x}^{\infty }{\frac {\mathrm {d} t}{t\left(t^{2}-1\right)\log t}}.

Опять же, формула справедлива для $x > 1$ , а $ρ$ — нетривиальные нули дзета-функции, упорядоченные по их абсолютному значению. Интеграл равен ряду по тривиальным нулям:

\int _{x}^{\infty }{\frac {\mathrm {d} t}{t\left(t^{2}-1\right)\log t}}=\int _{x}^{\infty }{\frac {1}{t\log t}}\left(\sum _{m}t^{-2m}\right)\,\mathrm {d} t=\sum _{m}\int _{x}^{\infty }{\frac {t^{-2m}}{t\log t}}\,\mathrm {d} t\,\,{\overset {\left(u=t^{-2m}\right)}{=}}-\sum _{m}\operatorname {li} \left(x^{-2m}\right)

Первый член $li(x)$ представляет собой обычную логарифмическую интегральную функцию ; выражение $li(x р)$ во втором члене следует рассматривать как $Ei(ρ log x)$ , где $Ei$ — аналитическое продолжение экспоненциальной интегральной функции от отрицательных действительных чисел до комплексной плоскости с ветвью, разрезанной вдоль положительных действительных чисел.

Таким образом, формула обращения Мёбиуса дает нам ^[10]

\pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} \left(x^{\rho }\right)-\sum _{m}\operatorname {R} \left(x^{-2m}\right)

справедливо для $x > 1$ , где

\operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} \left(x^{1/n}\right)=1+\sum _{k=1}^{\infty }{\frac {\left(\log x\right)^{k}}{k!k\zeta (k+1)}}

это R-функция Римана ^[22]и $µ (n)$ — функция Мёбиуса . Последняя серия для него известна как серия Грама . ^[23]^[24] Поскольку $log x < x$ для всех $x > 0$ , этот ряд сходится для всех положительных $x$ по сравнению с рядом для $e Икс$ . Логарифм в ряду Грама суммы по нетривиальному нулевому вкладу следует оценивать как $ρ log x$ , а не $log x. р$ .

Фолькмар Борнеманн протестировал, ^[25] если принять гипотезу о том, что все нули дзета-функции Римана простые, ^{[примечание 1]} что

\operatorname {R} \left(e^{-2\pi t}\right)={\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}t^{-2k-1}}{(2k+1)\zeta (2k+1)}}+{\frac {1}{2}}\sum _{\rho }{\frac {t^{-\rho }}{\rho \cos {\frac {\pi \rho }{2}}\zeta '(\rho )}}

где $ρ$ пробегает нетривиальные нули дзета-функции Римана и $t > 0$ .

Сумма по нетривиальным дзета-нулям в формуле для $π 0 (x)$ описывает колебания $π 0 (x)$ , в то время как остальные члены дают «гладкую» часть функции подсчета простых чисел, ^[26] так что можно использовать

\operatorname {R} (x)-\sum _{m=1}^{\infty }\operatorname {R} \left(x^{-2m}\right)

как хорошая оценка $π (x)$ для $x > 1$ . Фактически, поскольку второй член приближается к 0 при $x \to \infty$ , а амплитуда «шумной» части эвристически равна примерно $\sqrt x / log x$ оценка $π (x)$ только по $R(x)$ столь же хороша, а колебания распределения простых чисел могут быть четко представлены с помощью функции

{\bigl (}\pi _{0}(x)-\operatorname {R} (x){\bigr )}{\frac {\log x}{\sqrt {x}}}.

Неравенства [ править ]

Вот несколько полезных неравенств для $π (x)$ .

{\frac {x}{\log x}}<\pi (x)<1.25506{\frac {x}{\log x}}

для $х \geq 17$ .

Левое неравенство справедливо для $x \geq 17$ , а правое неравенство справедливо для $x > 1$ . Константа 1,25506 равна $30 log 113/113 до как$ 5 десятичных знаков, $π (x) log x / x$ имеет максимальное значение при $x = 113$ . ^[27]

Пьер Дюсар доказал в 2010 году: ^[28]

{\frac {x}{\log x-1}}<\pi (x)\quad {\text{for }}x\geq 5393,

и

\pi (x)<{\frac {x}{\log x-1.1}}\quad {\text{for }}x\geq 60184.

Вот некоторые неравенства для $n$ -го простого $pn числа$ . Верхняя оценка принадлежит Россеру (1941): ^[29] нижний - Дюсарту (1999): ^[30]

$n(\log(n\log n)-1)<p_{n}<n{\log(n\log n)}\quad {\text{for }}n\geq 6.$

Левое неравенство справедливо для $n \geq 2$ , а правое неравенство справедливо для $n \geq 6$ .

Приближение n- го простого числа:

p_{n}=n(\log(n\log n)-1)+{\frac {n(\log \log n-2)}{\log n}}+O\left({\frac {n(\log \log n)^{2}}{(\log n)^{2}}}\right).

Рамануджан ^[31] доказал, что неравенство

\pi (x)^{2}<{\frac {ex}{\log x}}\pi \left({\frac {x}{e}}\right)

справедливо для всех достаточно больших значений $x$ .

В 2010 ^[28] Дюсарт доказал (предложение 6.6), что для $n \geq$ 688383

p_{n}\leq n\left(\log n+\log \log n-1+{\frac {\log \log n-2}{\log n}}\right),

и (предложение 6.7) что при $n \geq$ 3

p_{n}\geq n\left(\log n+\log \log n-1+{\frac {\log \log n-2.1}{\log n}}\right).

Совсем недавно Дюсарт ^[32] доказал (теорема 5.1), что при $x >$ 1

\pi (x)\leq {\frac {x}{\log x}}\left(1+{\frac {1}{\log x}}+{\frac {2}{\log ^{2}x}}+{\frac {7.59}{\log ^{3}x}}\right),

и что для $x \geq$ 88789

\pi (x)>{\frac {x}{\log x}}\left(1+{\frac {1}{\log x}}+{\frac {2}{\log ^{2}x}}\right).

Гипотеза Римана [ править ]

Гипотеза Римана предполагает гораздо более жесткую границу ошибки оценки $π (x)$ и, следовательно, более регулярное распределение простых чисел:

\pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\log {x}).

Конкретно, ^[33]

|\pi (x)-\operatorname {li} (x)|<{\frac {\sqrt {x}}{8\pi }}\,\log {x},\quad {\text{for all }}x\geq 2657.

Дудек (2015) доказал, что из гипотезы Римана следует, что для всех $x \geq 2$ существует простое число $p$ , удовлетворяющее условиям

x-{\frac {4}{\pi }}{\sqrt {x}}\log x<p\leq x.

См. также [ править ]

Ссылки [ править ]

^ Бах, Эрик; Шалит, Джеффри (1996). Алгоритмическая теория чисел . МТИ Пресс. том 1 стр. 234 раздел 8.8. ISBN 0-262-02405-5 .
^ Вайсштейн, Эрик В. «Счетная функция простых чисел» . Математический мир .
^ «Сколько существует простых чисел?» . Крис К. Колдуэлл. Архивировано из оригинала 15 октября 2012 г. Проверено 2 декабря 2008 г.
^ Диксон, Леонард Юджин (2005). История теории чисел, Том. Я: Делимость и первичность . Дуврские публикации. ISBN 0-486-44232-2 .
^ Ирландия, Кеннет; Розен, Майкл (1998). Классическое введение в современную теорию чисел (второе изд.). Спрингер. ISBN 0-387-97329-Х .
^ См. также теорему 23 из А.Э. Ингхэм (2000). Распределение простых чисел . Издательство Кембриджского университета. ISBN 0-521-39789-8 .
^ Кевин Форд (ноябрь 2002 г.). «Интеграл Виноградова и границы дзета-функции Римана» (PDF) . Учеб. Лондонская математика. Соц . 85 (3): 565–633. arXiv : 1910.08209 . дои : 10.1112/S0024611502013655 . S2CID 121144007 .
^ Моссингхофф, Майкл Дж.; Трудджиан, Тимоти С. (2015). «Неотрицательные тригонометрические полиномы и область без нуля для дзета-функции Римана». Дж. Теория чисел . 157 : 329–349. arXiv : 1410.3926 . дои : 10.1016/J.JNT.2015.05.010 . S2CID 117968965 .
^ Хутама, Дэниел (2017). «Реализация явной формулы Римана для рациональных и гауссовских простых чисел в Sage» (PDF) . Институт математических наук .
^ Перейти обратно: ^а ^б Ризель, Ганс ; Гёль, Гуннар (1970). «Некоторые расчеты, связанные с формулой простых чисел Римана» (PDF) . Математика вычислений . 24 (112). Американское математическое общество: 969–983. дои : 10.2307/2004630 . ISSN 0025-5718 . JSTOR 2004630 . МР 0277489 .
^ «Условное вычисление π(10 ²⁴)» . Крис К. Колдуэлл . Проверено 30 марта 2024 г. .
^ Платт, Дэвид Дж. (2012). «Аналитическое вычисление $π (x)$ ». arXiv : 1203.5712 [ math.NT ].
^ «Сколько существует простых чисел?» . Дж. Бюте . Проверено 1 сентября 2015 г.
^ Стейпл, Дуглас (19 августа 2015 г.). Комбинаторный алгоритм вычисления π(x) (Диссертация). Университет Далхаузи . Проверено 1 сентября 2015 г.
^ Валиш, Ким (6 сентября 2015 г.). «Новое подтвержденное π(10 ²⁷) функция подсчета простых чисел "запись" . Форум Мерсенна .
^ Боуг, Дэвид (30 августа 2020 г.). «Новая запись функции подсчета простых чисел, пи(10^28)» . Форум Мерсенна .
^ Валиш, Ким (4 марта 2022 г.). «Новая запись функции подсчета простых чисел: PrimePi(10^29)» . Форум Мерсенна .
^ Лемер, Деррик Генри (1 апреля 1958 г.). «О точном количестве простых чисел меньше заданного предела» . Иллинойс Дж. Математика . 3 (3): 381–388 . Проверено 1 февраля 2017 г.
^ Делеглиз, Марк; Риват, Джоэл (январь 1996 г.). «Вычисление $π (x)$ : метод Мейселя, Лемера, Лагариаса, Миллера, Одлизко» (PDF) . Математика вычислений . 65 (213): 235–245. дои : 10.1090/S0025-5718-96-00674-6 .
^ Апостол, Том М. (2010). Введение в аналитическую теорию чисел . Спрингер.
^ Титчмарш, EC (1960). Теория функций, 2-е изд . Издательство Оксфордского университета.
^ Вайсштейн, Эрик В. «Функция подсчета простых чисел Римана» . Математический мир .
^ Ризель, Ганс (1994). Простые числа и компьютерные методы факторизации . Прогресс в математике. Том. 126 (2-е изд.). Биркхойзер. стр. 50–51. ISBN 0-8176-3743-5 .
^ Вайсштейн, Эрик В. «Серия граммов» . Математический мир .
^ Борнеманн, Фолькмар. «Решение проблемы, поставленной Йоргом Вальдфогелем» (PDF) .
^ «Кодирование простого распределения дзета-нулями» . Мэтью Уоткинс . Проверено 14 сентября 2008 г.
^ Россер, Дж. Баркли ; Шенфельд, Лоуэлл (1962). «Приближенные формулы для некоторых функций простых чисел» . Иллинойс Дж. Математика . 6 : 64–94. дои : 10.1215/ijm/1255631807 . ISSN 0019-2082 . Збл 0122.05001 .
^ Перейти обратно: ^а ^б Дюсар, Пьер (2 февраля 2010 г.). «Оценки некоторых функций над простыми числами без RH». arXiv : 1002.0442v1 [ math.NT ].
^ Россер, Баркли (1941). «Явные оценки некоторых функций простых чисел». Американский журнал математики . 63 (1): 211–232. дои : 10.2307/2371291 . JSTOR 2371291 .
^ Дюсар, Пьер (1999). « К -е простое число больше k (ln k + ln ln k − 1) для k ≥ 2» . Математика вычислений . 68 (225): 411–415. дои : 10.1090/S0025-5718-99-01037-6 .
^ Берндт, Брюс К. (6 декабря 2012 г.). Записные книжки Рамануджана, часть IV . Springer Science & Business Media. стр. 112–113. ISBN 9781461269328 .
^ Дюсар, Пьер (январь 2018 г.). «Явные оценки некоторых функций над простыми числами». Журнал Рамануджана . 45 (1): 225–234. дои : 10.1007/s11139-016-9839-4 . S2CID 125120533 .
^ Шенфельд, Лоуэлл (1976). «Уточнение оценок функций Чебышева θ ( x ) и ψ ( x ). II». Математика вычислений . 30 (134). Американское математическое общество: 337–360. дои : 10.2307/2005976 . ISSN 0025-5718 . JSTOR 2005976 . МР 0457374 .

Примечания [ править ]

^ Монтгомери показал, что (при условии гипотезы Римана) по крайней мере две трети всех нулей простые.

Внешние ссылки [ править ]

Крис Колдуэлл, The Nth Prime Page в The Prime Pages .
Томас Оливейра и Сильва, Таблицы функций подсчета простых чисел .
Дудек, Адриан В. (2015), «О гипотезе Римана и разнице между простыми числами», Международный журнал теории чисел , 11 (3): 771–778, arXiv : 1402.6417 , Bibcode : 2014arXiv1402.6417D , doi : 10.1142/ С1793042115500426 , ISSN 1793-0421 , S2CID 119321107

[Bach-1] Бах, Эрик; Шалит, Джеффри (1996). Алгоритмическая теория чисел . МТИ Пресс. том 1 стр. 234 раздел 8.8. ISBN 0-262-02405-5 .

[mathworld_pcf-2] Вайсштейн, Эрик В. «Счетная функция простых чисел» . Математический мир .

[Caldwell-3] «Сколько существует простых чисел?» . Крис К. Колдуэлл. Архивировано из оригинала 15 октября 2012 г. Проверено 2 декабря 2008 г.

[Dickson-4] Диксон, Леонард Юджин (2005). История теории чисел, Том. Я: Делимость и первичность . Дуврские публикации. ISBN 0-486-44232-2 .

[Ireland-5] Ирландия, Кеннет; Розен, Майкл (1998). Классическое введение в современную теорию чисел (второе изд.). Спрингер. ISBN 0-387-97329-Х .

[6] См. также теорему 23 из А.Э. Ингхэм (2000). Распределение простых чисел . Издательство Кембриджского университета. ISBN 0-521-39789-8 .

[Ford-7] Кевин Форд (ноябрь 2002 г.). «Интеграл Виноградова и границы дзета-функции Римана» (PDF) . Учеб. Лондонская математика. Соц . 85 (3): 565–633. arXiv : 1910.08209 . дои : 10.1112/S0024611502013655 . S2CID 121144007 .

[8] Моссингхофф, Майкл Дж.; Трудджиан, Тимоти С. (2015). «Неотрицательные тригонометрические полиномы и область без нуля для дзета-функции Римана». Дж. Теория чисел . 157 : 329–349. arXiv : 1410.3926 . дои : 10.1016/J.JNT.2015.05.010 . S2CID 117968965 .

[9] Хутама, Дэниел (2017). «Реализация явной формулы Римана для рациональных и гауссовских простых чисел в Sage» (PDF) . Институт математических наук .

[RieselGohl-10] Перейти обратно: ^а ^б Ризель, Ганс ; Гёль, Гуннар (1970). «Некоторые расчеты, связанные с формулой простых чисел Римана» (PDF) . Математика вычислений . 24 (112). Американское математическое общество: 969–983. дои : 10.2307/2004630 . ISSN 0025-5718 . JSTOR 2004630 . МР 0277489 .

[Franke-11] «Условное вычисление π(10 ²⁴)» . Крис К. Колдуэлл . Проверено 30 марта 2024 г. .

[PlattARXIV2012-12] Платт, Дэвид Дж. (2012). «Аналитическое вычисление $π (x)$ ». arXiv : 1203.5712 [ math.NT ].

[Buethe-13] «Сколько существует простых чисел?» . Дж. Бюте . Проверено 1 сентября 2015 г.

[Staple-14] Стейпл, Дуглас (19 августа 2015 г.). Комбинаторный алгоритм вычисления π(x) (Диссертация). Университет Далхаузи . Проверено 1 сентября 2015 г.

[15] Валиш, Ким (6 сентября 2015 г.). «Новое подтвержденное π(10 ²⁷) функция подсчета простых чисел "запись" . Форум Мерсенна .

[16] Боуг, Дэвид (30 августа 2020 г.). «Новая запись функции подсчета простых чисел, пи(10^28)» . Форум Мерсенна .

[17] Валиш, Ким (4 марта 2022 г.). «Новая запись функции подсчета простых чисел: PrimePi(10^29)» . Форум Мерсенна .

[lehmer-18] Лемер, Деррик Генри (1 апреля 1958 г.). «О точном количестве простых чисел меньше заданного предела» . Иллинойс Дж. Математика . 3 (3): 381–388 . Проверено 1 февраля 2017 г.

[pix_comp-19] Делеглиз, Марк; Риват, Джоэл (январь 1996 г.). «Вычисление $π (x)$ : метод Мейселя, Лемера, Лагариаса, Миллера, Одлизко» (PDF) . Математика вычислений . 65 (213): 235–245. дои : 10.1090/S0025-5718-96-00674-6 .

[20] Апостол, Том М. (2010). Введение в аналитическую теорию чисел . Спрингер.

[Titchmarsh-21] Титчмарш, EC (1960). Теория функций, 2-е изд . Издательство Оксфордского университета.

[mathworld_r-22] Вайсштейн, Эрик В. «Функция подсчета простых чисел Римана» . Математический мир .

[Riesel94-23] Ризель, Ганс (1994). Простые числа и компьютерные методы факторизации . Прогресс в математике. Том. 126 (2-е изд.). Биркхойзер. стр. 50–51. ISBN 0-8176-3743-5 .

[mathworld_gram-24] Вайсштейн, Эрик В. «Серия граммов» . Математический мир .

[25] Борнеманн, Фолькмар. «Решение проблемы, поставленной Йоргом Вальдфогелем» (PDF) .

[Watkins-27] «Кодирование простого распределения дзета-нулями» . Мэтью Уоткинс . Проверено 14 сентября 2008 г.

[28] Россер, Дж. Баркли ; Шенфельд, Лоуэлл (1962). «Приближенные формулы для некоторых функций простых чисел» . Иллинойс Дж. Математика . 6 : 64–94. дои : 10.1215/ijm/1255631807 . ISSN 0019-2082 . Збл 0122.05001 .

[Dusart2010-29] Перейти обратно: ^а ^б Дюсар, Пьер (2 февраля 2010 г.). «Оценки некоторых функций над простыми числами без RH». arXiv : 1002.0442v1 [ math.NT ].

[30] Россер, Баркли (1941). «Явные оценки некоторых функций простых чисел». Американский журнал математики . 63 (1): 211–232. дои : 10.2307/2371291 . JSTOR 2371291 .

[31] Дюсар, Пьер (1999). « К -е простое число больше k (ln k + ln ln k − 1) для k ≥ 2» . Математика вычислений . 68 (225): 411–415. дои : 10.1090/S0025-5718-99-01037-6 .

[32] Берндт, Брюс К. (6 декабря 2012 г.). Записные книжки Рамануджана, часть IV . Springer Science & Business Media. стр. 112–113. ISBN 9781461269328 .

[33] Дюсар, Пьер (январь 2018 г.). «Явные оценки некоторых функций над простыми числами». Журнал Рамануджана . 45 (1): 225–234. дои : 10.1007/s11139-016-9839-4 . S2CID 125120533 .

[34] Шенфельд, Лоуэлл (1976). «Уточнение оценок функций Чебышева θ ( x ) и ψ ( x ). II». Математика вычислений . 30 (134). Американское математическое общество: 337–360. дои : 10.2307/2005976 . ISSN 0025-5718 . JSTOR 2005976 . МР 0457374 .

[26] Монтгомери показал, что (при условии гипотезы Римана) по крайней мере две трети всех нулей простые.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[примечание 1]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]