Экспоненциальный интеграл

Не путать с другими интегралами показательных функций .

График экспоненциальной интегральной функции E n(z) с n=2 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

В математике экспоненциальный интеграл Ei — это специальная функция на комплексной плоскости .

Он определяется как один определенный интеграл отношения между показательной функцией и ее аргументом .

Определения

Для действительных ненулевых значений x экспоненциальный интеграл Ei( x ) определяется как

$\operatorname {Ei} (x)=-\int _{-x}^{\infty }{\frac {e^{-t}}{t}}\,dt=\int _{-\infty }^{x}{\frac {e^{t}}{t}}\,dt.$

Алгоритм Риша показывает, что Ei не является элементарной функцией . Приведенное выше определение можно использовать для положительных значений x , но интеграл следует понимать в терминах главного значения Коши из -за особенности подынтегральной функции в нуле.

Для комплексных значений аргумента определение становится неоднозначным из-за точек ветвления в точках 0 и $\infty$. Вместо Ei используются следующие обозначения:

$E_{1}(z)=\int _{z}^{\infty }{\frac {e^{-t}}{t}}\,dt,\qquad |{\rm {Arg}}(z)|<\pi$

График экспоненциальной интегральной функции Ei(z) в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

Для положительных значений x мы имеем $-E_{1}(x)=\operatorname {Ei} (-x)$.

В общем случае разрез ветки делается на отрицательной действительной оси, и E ₁ может быть определен путем аналитического продолжения в другом месте комплексной плоскости.

При положительных значениях действительной части $z$, это можно написать

$E_{1}(z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}\,dt=\int _{0}^{1}{\frac {e^{-z/u}}{u}}\,du,\qquad \Re (z)\geq 0.$

Поведение E ₁ вблизи среза ветки можно увидеть по следующему соотношению:

$\lim _{\delta \to 0+}E_{1}(-x\pm i\delta )=-\operatorname {Ei} (x)\mp i\pi ,\qquad x>0.$

Свойства

Некоторые свойства экспоненциального интеграла, приведенные ниже, в некоторых случаях позволяют избежать его явного вычисления посредством приведенного выше определения.

Сходящийся ряд

Сюжет $E_{1}$ функция (вверху) и $\operatorname {Ei}$ функция (внизу).

Для реальных или сложных аргументов, выходящих за пределы отрицательной действительной оси, $E_{1}(z)$ может быть выражено как

$E_{1}(z)=-\gamma -\ln z-\sum _{k=1}^{\infty }{\frac {(-z)^{k}}{k\;k!}}\qquad (\left|\operatorname {Arg} (z)\right|<\pi )$

где $\gamma$ – постоянная Эйлера–Машерони . Сумма сходится для всех комплексных $z$, и берем обычное значение комплексного логарифма, имеющего разрез по отрицательной вещественной оси.

Эту формулу можно использовать для вычисления $E_{1}(x)$ с операциями с плавающей запятой на самом деле $x$ от 0 до 2,5. Для $x>2.5$, результат неточный из-за отмены .

нашел более быстро сходящийся ряд Рамануджан :

${\rm {Ei}}(x)=\gamma +\ln x+\exp {(x/2)}\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}x^{n}}{n!\,2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}$

(расходящийся

Относительная погрешность асимптотического приближения для разных чисел $~N~$ членов в усеченной сумме

К сожалению, сходимость приведенного выше ряда происходит медленно для аргументов большего модуля. Например, для получения правильного ответа с точностью до трех значащих цифр требуется более 40 терминов. $E_{1}(10)$. Однако для положительных значений x существует аппроксимация расходящимся рядом, которую можно получить путем интегрирования $xe^{x}E_{1}(x)$ по частям:

$E_{1}(x)={\frac {\exp(-x)}{x}}\left(\sum _{n=0}^{N-1}{\frac {n!}{(-x)^{n}}}+O(N!x^{-N})\right)$

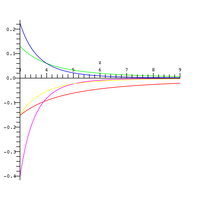
Относительная погрешность приведенного выше приближения показана на рисунке справа для различных значений $N$, количество членов в усеченной сумме ( $N=1$ в красном, $N=5$ розового цвета).

Асимптотика вне всех порядков

Интегрируя по частям, можно получить явную формулу

$$\operatorname {Ei} (z)={\frac {e^{z}}{z}}\left(\sum _{k=0}^{n}{\frac {k!}{z^{k}}}+e_{n}(z)\right),\quad e_{n}(z)\equiv (n+1)!\ ze^{-z}\int _{-\infty }^{z}{\frac {e^{t}}{t^{n+2}}}\,dt$$

Для любого фиксированного $z$, абсолютное значение ошибки $|e_{n}(z)|$ уменьшается, затем увеличивается. Минимум возникает при $n\sim |z|$, в этот момент $\vert e_{n}(z)\vert \leq {\sqrt {\frac {2\pi }{\vert z\vert }}}e^{-\vert z\vert }$. Эта граница называется «асимптотикой вне всех порядков».

Экспоненциальное и логарифмическое поведение: брекетинг

Брекетинг $E_{1}$ по элементарным функциям

Из двух серий, предложенных в предыдущих подразделах, следует, что $E_{1}$ ведет себя как отрицательная экспонента для больших значений аргумента и как логарифм для малых значений. Для положительных действительных значений аргумента $E_{1}$ могут быть заключены в скобки элементарными функциями следующим образом:

${\frac {1}{2}}e^{-x}\,\ln \!\left(1+{\frac {2}{x}}\right)<E_{1}(x)<e^{-x}\,\ln \!\left(1+{\frac {1}{x}}\right)\qquad x>0$

Левая часть этого неравенства показана на графике слева синим цветом; центральная часть $E_{1}(x)$ показан черным цветом, а правая часть — красным.

Определение Эйна

Оба $\operatorname {Ei}$ и $E_{1}$ можно записать проще, используя всю функцию $\operatorname {Ein}$ определяется как

$\operatorname {Ein} (z)=\int _{0}^{z}(1-e^{-t}){\frac {dt}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{k\;k!}}$

(обратите внимание, что это всего лишь знакопеременный ряд в приведенном выше определении $E_{1}$). Тогда у нас есть

$E_{1}(z)\,=\,-\gamma -\ln z+{\rm {Ein}}(z)\qquad \left|\operatorname {Arg} (z)\right|<\pi$

$\operatorname {Ei} (x)\,=\,\gamma +\ln {x}-\operatorname {Ein} (-x)\qquad x\neq 0$

Связь с другими функциями

Уравнение Куммера

$z{\frac {d^{2}w}{dz^{2}}}+(b-z){\frac {dw}{dz}}-aw=0$

обычно решается с помощью вырожденных гипергеометрических функций $M(a,b,z)$ и $U(a,b,z).$ Но когда $a=0$ и $b=1,$ то есть,

$z{\frac {d^{2}w}{dz^{2}}}+(1-z){\frac {dw}{dz}}=0$

у нас есть

$M(0,1,z)=U(0,1,z)=1$

для всех з . Второе решение тогда дается E ₁ (− z ). Фактически,

$E_{1}(-z)=-\gamma -i\pi +{\frac {\partial [U(a,1,z)-M(a,1,z)]}{\partial a}},\qquad 0<{\rm {Arg}}(z)<2\pi$

с производной, оцененной в $a=0.$ Другая связь с вырожденными гипергеометрическими функциями состоит в том, что E ₁ представляет собой экспоненциальное произведение функции U (1,1, z ):

$E_{1}(z)=e^{-z}U(1,1,z)$

Экспоненциальный интеграл тесно связан с логарифмической интегральной функцией li( x ) формулой

$\operatorname {li} (e^{x})=\operatorname {Ei} (x)$

для ненулевых действительных значений $x$.

Обобщение

Экспоненциальный интеграл также можно обобщить на

$E_{n}(x)=\int _{1}^{\infty }{\frac {e^{-xt}}{t^{n}}}\,dt,$

которую можно записать как частный случай верхней неполной гамма-функции :

$E_{n}(x)=x^{n-1}\Gamma (1-n,x).$

Обобщенную форму иногда называют функцией Мисры. $\varphi _{m}(x)$, определяемый как

$\varphi _{m}(x)=E_{-m}(x).$

Многие свойства этой обобщенной формы можно найти в цифровой библиотеке математических функций NIST.

Включение логарифма определяет обобщенную интегро-экспоненциальную функцию

$E_{s}^{j}(z)={\frac {1}{\Gamma (j+1)}}\int _{1}^{\infty }\left(\log t\right)^{j}{\frac {e^{-zt}}{t^{s}}}\,dt.$

Неопределенный интеграл:

$\operatorname {Ei} (a\cdot b)=\iint e^{ab}\,da\,db$

по форме аналогична обычной производящей функции для $d(n)$ количество делителей , $n$:

$\sum \limits _{n=1}^{\infty }d(n)x^{n}=\sum \limits _{a=1}^{\infty }\sum \limits _{b=1}^{\infty }x^{ab}$

Производные

Производные обобщенных функций $E_{n}$ можно рассчитать по формуле

$E_{n}'(z)=-E_{n-1}(z)\qquad (n=1,2,3,\ldots )$

Обратите внимание, что функция $E_{0}$ легко оценить (что делает эту рекурсию полезной), поскольку она просто $e^{-z}/z$.

Экспоненциальный интеграл от мнимого аргумента

$E_{1}(ix)$ против $x$; Реальная часть черная, мнимая часть красная.

Если $z$ является мнимым, имеет неотрицательную действительную часть, поэтому мы можем использовать формулу

$E_{1}(z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}\,dt$

чтобы получить связь с тригонометрическими интегралами $\operatorname {Si}$ и $\operatorname {Ci}$:

$E_{1}(ix)=i\left[-{\tfrac {1}{2}}\pi +\operatorname {Si} (x)\right]-\operatorname {Ci} (x)\qquad (x>0)$

Действительная и мнимая части $\mathrm {E} _{1}(ix)$ на рисунке справа изображены черными и красными кривыми.

Приближения

Существует ряд приближений экспоненциальной интегральной функции. К ним относятся:

• Приближение Свами и Охиджи
  $$E_{1}(x)=\left(A^{-7.7}+B\right)^{-0.13},$$
  где
  $${\begin{aligned}A&=\ln \left[\left({\frac {0.56146}{x}}+0.65\right)(1+x)\right]\\B&=x^{4}e^{7.7x}(2+x)^{3.7}\end{aligned}}$$
• Приближение Аллена и Гастингса
  $$E_{1}(x)={\begin{cases}-\ln x+{\textbf {a}}^{T}{\textbf {x}}_{5},&x\leq 1\\{\frac {e^{-x}}{x}}{\frac {{\textbf {b}}^{T}{\textbf {x}}_{3}}{{\textbf {c}}^{T}{\textbf {x}}_{3}}},&x\geq 1\end{cases}}$$
  где
  $${\begin{aligned}{\textbf {a}}&\triangleq [-0.57722,0.99999,-0.24991,0.05519,-0.00976,0.00108]^{T}\\{\textbf {b}}&\triangleq [0.26777,8.63476,18.05902,8.57333]^{T}\\{\textbf {c}}&\triangleq [3.95850,21.09965,25.63296,9.57332]^{T}\\{\textbf {x}}_{k}&\triangleq [x^{0},x^{1},\dots ,x^{k}]^{T}\end{aligned}}$$
• Продолжающееся расширение фракции
  $$E_{1}(x)={\cfrac {e^{-x}}{x+{\cfrac {1}{1+{\cfrac {1}{x+{\cfrac {2}{1+{\cfrac {2}{x+{\cfrac {3}{\ddots }}}}}}}}}}}}.$$
• Аппроксимация Barry et al.
  $$E_{1}(x)={\frac {e^{-x}}{G+(1-G)e^{-{\frac {x}{1-G}}}}}\ln \left[1+{\frac {G}{x}}-{\frac {1-G}{(h+bx)^{2}}}\right],$$
  где:
  $${\begin{aligned}h&={\frac {1}{1+x{\sqrt {x}}}}+{\frac {h_{\infty }q}{1+q}}\\q&={\frac {20}{47}}x^{\sqrt {\frac {31}{26}}}\\h_{\infty }&={\frac {(1-G)(G^{2}-6G+12)}{3G(2-G)^{2}b}}\\b&={\sqrt {\frac {2(1-G)}{G(2-G)}}}\\G&=e^{-\gamma }\end{aligned}}$$
  с $\gamma$ постоянная Эйлера -Машерони .

экспоненциального

Мы можем выразить обратную функцию экспоненциального интеграла в виде степенного ряда :

$\forall |x|<{\frac {\mu }{\ln(\mu )}},\quad \mathrm {Ei} ^{-1}(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}{\frac {P_{n}(\ln(\mu ))}{\mu ^{n}}}$

где $\mu$ – константа Рамануджана–Солднера и $(P_{n})$ представляет собой полиномиальную последовательность, определяемую следующим рекуррентным соотношением :

$P_{0}(x)=x,\ P_{n+1}(x)=x(P_{n}'(x)-nP_{n}(x)).$

Для $n>0$, $\deg P_{n}=n$ и у нас есть формула:

$P_{n}(x)=\left.\left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)^{n-1}\left({\frac {te^{x}}{\mathrm {Ei} (t+x)-\mathrm {Ei} (x)}}\right)^{n}\right|_{t=0}.$

Приложения

• Зависящая от времени теплопередача
• Неравновесный поток подземных вод в решении Тайса (называемый функцией скважины )
• Перенос излучения в звездных и планетных атмосферах
• Уравнение радиальной диффузии для переходного или нестационарного течения с линейными источниками и стоками
• Решения уравнения переноса нейтронов в упрощенной одномерной геометрии

См. также

• Интеграл Гудвина – Стейтона
• Функции Бикли – Нейлора

Ссылки

• Абрамовиц, Милтон; Ирен Стегун (1964). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Абрамовиц и Стегун . Нью-Йорк: Дувр. ISBN  978-0-486-61272-0 . , Глава 5 .
• Бендер, Карл М.; Стивен А. Орзаг (1978). Передовые математические методы для ученых и инженеров . МакГроу-Хилл. ISBN  978-0-07-004452-4 .
• Блейстейн, Норман; Ричард А. Хандельсман (1986). Асимптотические разложения интегралов . Дувр. ISBN  978-0-486-65082-1 .
• Басбридж, Ида В. (1950). «Об интегро-экспоненциальной функции и вычислении некоторых связанных с ней интегралов». Кварта. Дж. Математика. (Оксфорд) . 1 (1): 176–184. Бибкод : 1950QJMat...1..176B . дои : 10.1093/qmath/1.1.176 .
• Станкевич, А. (1968). «Таблицы интегро-показательных функций». Акта Астрономика . 18 : 289. Бибкод : 1968AcA....18..289S .
• Шарма, РР; Зохури, Бахман (1977). «Общий метод точного вычисления экспоненциальных интегралов E ₁ (x), x>0». Дж. Компьютер. Физ . 25 (2): 199–204. Бибкод : 1977JCoPh..25..199S . дои : 10.1016/0021-9991(77)90022-5 .
• Кёлбиг, К.С. (1983). «Об интеграле exp(− µt ) t ⁿ⁻¹ бревно ^м t   dt " . Math. Comput . 41 (163): 171–182. doi : 10.1090/S0025-5718-1983-0701632-1 .
• Милгрэм, MS (1985). «Обобщенная интегро-экспоненциальная функция» . Математика вычислений . 44 (170): 443–458. дои : 10.1090/S0025-5718-1985-0777276-4 . JSTOR   2007964 . МР   0777276 .
• Мишра, Рама Дхар; Борн, М. (1940). «Об устойчивости кристаллических решеток. II». Математические труды Кембриджского философского общества . 36 (2): 173. Бибкод : 1940PCPS...36..173M . дои : 10.1017/S030500410001714X . S2CID   251097063 .
• Чикколи, К.; Лоренцутта, С.; Майно, Г. (1988). «О вычислении обобщенных экспоненциальных интегралов E _ν (x)». Дж. Компьютер. Физ . 78 (2): 278–287. Бибкод : 1988JCoPh..78..278C . дои : 10.1016/0021-9991(88)90050-2 .
• Чикколи, К.; Лоренцутта, С.; Майно, Г. (1990). «Последние результаты для обобщенных экспоненциальных интегралов» . Компьютерная математика. Приложение . 19 (5): 21–29. дои : 10.1016/0898-1221(90)90098-5 .
• Маклауд, Аллан Дж. (2002). «Эффективное вычисление некоторых обобщенных экспоненциальных интегралов» . Дж. Компьютер. Прил. Математика . 148 (2): 363–374. дои : 10.1016/S0377-0427(02)00556-3 .
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 6.3. Экспоненциальные интегралы» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8 , заархивировано из оригинала 11 августа 2011 г. , получено 9 августа 2011 г.
• Темме, Нью-Мексико (2010), «Экспоненциальные, логарифмические, синусоидальные и косинусоидальные интегралы» , в Олвере, Фрэнке У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .

Внешние ссылки

• «Интегральная показательная функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Документация NIST по обобщенному экспоненциальному интегралу
• Вайсштейн, Эрик В. «Экспоненциальный интеграл» . Математический мир .
• Вайсштейн, Эрик В. « En -Function» . Математический мир .
• «Экспоненциальный интеграл Ei» . Wolfram . Сайт функций
• Экспоненциальные, логарифмические, синусоидальные и косинусоидальные интегралы в DLMF .