Решето Эратосфена

В математике решето Эратосфена — это древний алгоритм нахождения всех простых чисел до любого заданного предела.

Это достигается путем итеративной маркировки как составных (т. е. не простых) кратных каждого простого числа, начиная с первого простого числа, 2. Кратные данного простого числа генерируются как последовательность чисел, начиная с этого простого числа, с постоянной разницей. между ними , равное этому простому числу. ^[1] В этом ключевое отличие сита от использования пробного деления для последовательной проверки каждого числа-кандидата на делимость на каждое простое число. ^[2] Как только все кратные каждого обнаруженного простого числа будут помечены как составные, оставшиеся неотмеченные числа станут простыми.

Самое раннее известное упоминание о решете во Герасы « Введении . содержится Никомаха из » в арифметику ^[3]начало 2 в. Книга CE, которая приписывает его Эратосфену Киренскому , 3-му веку. до н.э. Греческий математик , хотя и описывал просеивание нечетными числами, а не простыми числами. ^[4]

Одно из множества сит простых чисел . Это один из наиболее эффективных способов найти все меньшие простые числа. Его можно использовать для нахождения простых чисел в арифметических прогрессиях . ^[5]

Обзор [ править ]

Просейте двойку и просейте тройку:
Решето Эратосфена.
Когда кратные возвышенны,
Оставшиеся числа являются простыми.

Анонимный ^[6]

Простое число — это натуральное число , которое имеет ровно два различных натуральных делителя : число 1 и само себя.

Чтобы найти все простые числа, меньшие или равные заданному целому $n,$ методом Эратосфена:

Создайте список последовательных целых чисел от 2 до $n$ : $(2, 3, 4, ..., n)$ .
Первоначально пусть $p$ равно 2, наименьшему простому числу.
Перечислите кратные $p$ , считая с шагом $p$ от $2 p$ до $n$ , и отметьте их в списке (это будут $2 p, 3 p, 4 p,...$ ; $сам p$ не должен быть отмечен).
Найдите в списке наименьшее число, большее $p$ , которое не отмечено. Если такого номера не было, остановитесь. В противном случае пусть $p$ теперь будет равно этому новому числу (которое является следующим простым числом) и повторите действия, начиная с шага 3.
Когда алгоритм завершает работу, все числа, оставшиеся незамеченными в списке, являются простыми числами ниже $n$ .

Основная идея здесь заключается в том, что каждое значение, присвоенное $p$ , будет простым, потому что, если бы оно было составным, оно было бы отмечено как кратное другому, меньшему простому числу. Обратите внимание, что некоторые числа могут быть отмечены более одного раза (например, 15 будет отмечено как для 3, так и для 5).

В качестве уточнения достаточно отметить числа в шаге 3, начиная с $p 2$ , поскольку все меньшие числа, кратные $p$ , уже будут отмечены в этот момент. Это означает, что алгоритм может завершиться на шаге 4, когда $p 2$ больше, чем $n$ . ^[1]

Другое усовершенствование состоит в том, чтобы изначально перечислять только нечетные числа $(3, 5, ..., n)$ и считать их с шагом $2 p$ на шаге 3, таким образом отмечая только нечетные числа, кратные $p$ . Это действительно присутствует в исходном алгоритме. ^[1]^[4] Это можно обобщить с помощью факторизации колеса , формируя исходный список только из чисел, взаимно простых с первыми несколькими простыми числами, а не только из чисел (т. е. чисел, взаимно простых с 2), и подсчитывая соответственно скорректированные приращения, чтобы только такие кратные $p$ были сгенерированные числа, взаимно простые с этими маленькими простыми числами. ^[7]

Пример [ править ]

Чтобы найти все простые числа, меньшие или равные 30, поступите следующим образом.

Сначала сгенерируйте список целых чисел от 2 до 30:

 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Первое число в списке — 2; вычеркнуть каждое 2-е число в списке после 2, считая от 2 с шагом 2 (это будут все кратные 2 в списке):

 2  3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30

Следующее число в списке после 2 — 3; вычеркнуть каждое 3-е число в списке после 3, считая от 3 с шагом 3 (это будут все кратные 3 в списке):

 2  3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30

Следующее еще не вычеркнутое число в списке после 3 — 5; вычеркнуть каждое пятое число в списке после 5, считая от 5 с шагом 5 (т.е. все числа, кратные 5):

 2  3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30

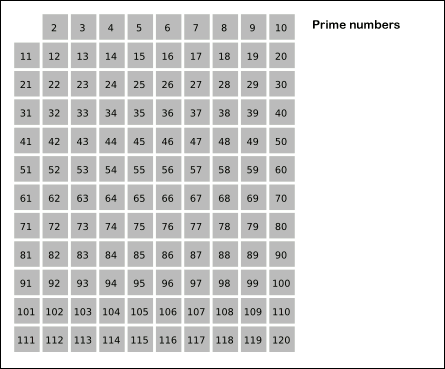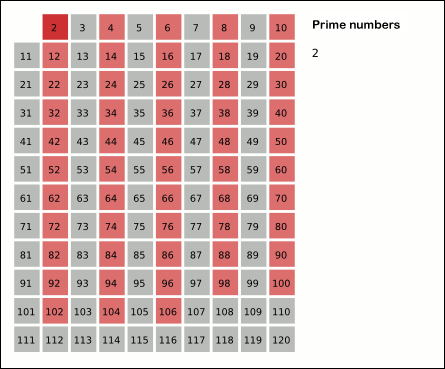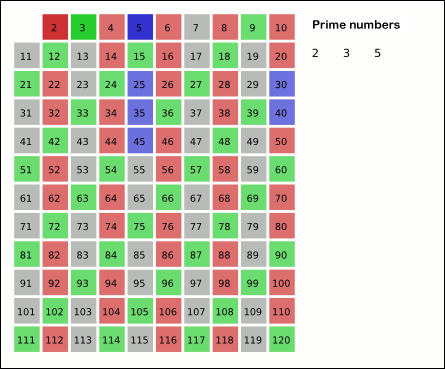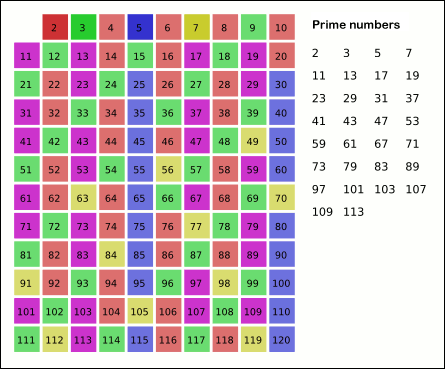
Следующее еще не вычеркнутое число в списке после 5 — это 7; следующим шагом будет вычеркивание каждого седьмого числа в списке после 7, но все они уже вычеркнуты на этом этапе, поскольку эти числа (14, 21, 28) также кратны меньшим простым числам, потому что 7 × 7 больше больше 30. Числа, не вычеркнутые на этом этапе списка, — это все простые числа ниже 30:

 2  3     5     7          11    13          17    19          23                29

Алгоритм и варианты [ править ]

Псевдокод [ править ]

Решето Эратосфена можно выразить в псевдокоде следующим образом: ^[8]^[9]

 алгоритма  Решето Эратосфена На 
     вход  : целое число  n  > 1. 
      вывод  : все простые числа от 2 до  n  . 

      пусть   A  будет  массивом  логических  значений, индексированных  целыми числами  от s 2 до  n  , 
      изначально все  установлено  в  true  . 
    
      для   i  = 2, 3, 4, ..., не превышающих  $\sqrt n$   делать 
         , если   A  [  i  ]  истинно   , 
             для   j  =  i ²,  я ²+  я  ,  я ²+2  я  ,  я ²+3  i  , ..., не превышающее  n,   сделать 
                 set   A  [  j  ] :=  false 

     вернуть  все  i  что  A  [  i  ]  истинно   такие ,  .

Этот алгоритм выдает все простые числа, не превышающие $n$ . Он включает в себя общую оптимизацию, которая заключается в том, чтобы начать перебор кратных каждого простого числа $i$ из $i. 2$ . Временная сложность этого алгоритма составляет $O (n log log n)$ , ^[9] при условии, что обновление массива представляет собой $операцию O (1)$ , как это обычно бывает.

Сегментированное сито [ править ]

Как отмечает Соренсон, проблема с решетом Эратосфена не в количестве операций, которые оно выполняет, а, скорее, в требованиях к памяти. ^[9]При больших $n$ диапазон простых чисел может не поместиться в памяти; хуже того, даже при умеренном $n$ крайне использование кэша неоптимально. Алгоритм проходит через весь массив $A$ , практически не обнаруживая локальности ссылки .

Решение этих проблем предлагают сегментированные сита, в которых одновременно просеивается только часть ассортимента. ^[10] Они известны с 1970-х годов и работают следующим образом: ^[9]^[11]

Разделите диапазон от 2 до $n$ на сегменты некоторого размера $Δ \leq \sqrt n$ .
Найдите простые числа в первом (то есть самом нижнем) сегменте, используя обычное сито.
Для каждого из следующих сегментов в порядке возрастания, где m — самое верхнее значение сегмента, найдите в нем простые числа следующим образом:
1. Настройте логический массив размера $Δ$ .
2. Отметьте как непростые позиции в массиве, соответствующие кратным каждому простому числу $p \leq \sqrt m$ , найденному на данный момент, путем перечисления его кратных с шагом $p$ , начиная с наименьшего кратного $p$ между $m - Δ$ и $m$ .
3. Остальные неотмеченные позиции в массиве соответствуют простым числам в отрезке. Нет необходимости отмечать кратные этим простым числам, поскольку все эти простые числа больше $\sqrt m$ , а для $k \geq 1$ имеем $(k\Delta +1)^{2}>(k+1)\Delta$ .

Если $Δ$ выбрано равным $\sqrt n$ , пространственная сложность алгоритма равна $O (\sqrt n)$ , а временная сложность такая же, как у обычного сита. ^[9]

Для диапазонов с верхним пределом $n$ настолько большим, что просеивающие простые числа ниже $\sqrt n$ , как того требует сегментированное по страницам решето Эратосфена, не могут поместиться в памяти, вместо этого можно использовать более медленное, но гораздо более экономное по пространству решето, такое как решето Соренсона . ^[12]

Инкрементное сито [ править ]

Инкрементная формулировка сита ^[2]генерирует простые числа бесконечно (т. е. без верхней границы), чередуя генерацию простых чисел с генерацией их кратных (так что простые числа можно найти в промежутках между кратными), где кратные каждому простому числу $p$ генерируются непосредственно путем подсчета от квадрата простого числа с шагом $p$ (или $2 p$ для нечетных простых чисел). Генерацию необходимо начинать только при достижении квадрата простого числа, чтобы избежать негативного влияния на эффективность. Это можно выразить символически в рамках парадигмы потока данных как

простые числа  = [  2  ,  3  , ...] \ [[  p  ²,  p  ²+  p  , ...] для  p  в  простых числах  ],

используя обозначение понимания списка с \ обозначающий множество вычитаний арифметических прогрессий чисел.

Простые числа также можно получить путем итеративного отсеивания составных чисел посредством проверки на делимость последовательными простыми числами, по одному простому числу за раз. Это не решето Эратосфена, но его часто путают, хотя решето Эратосфена непосредственно генерирует сложные соединения, а не проверяет их. Пробное деление имеет худшую теоретическую сложность , чем решето Эратосфена при создании диапазонов простых чисел. ^[2]

При проверке каждого простого числа алгоритм оптимального пробного деления использует все простые числа, не превышающие его квадратного корня, тогда как решето Эратосфена создает каждый составной элемент только из его простых множителей и получает простые числа «бесплатно» между составными числами. Широко известный код функционального сита 1975 года Дэвида Тернера. ^[13] часто представляют как пример решета Эратосфена. ^[7] но на самом деле это неоптимальное сито пробного деления. ^[2]

Алгоритмическая сложность [ править ]

Решето Эратосфена — популярный способ оценить производительность компьютера. ^[14]Временная сложность вычисления всех простых чисел ниже $n$ в модели машины произвольного доступа составляет $O (n log log n)$ операций, что является прямым следствием того факта, что ряд простых гармоник асимптотически приближается к $log log n$ . Однако он имеет экспоненциальную временную сложность относительно длины входных данных, что делает его псевдополиномиальным алгоритмом. Базовый алгоритм требует $O (n)$ памяти.

Битовая сложность алгоритма составляет $O (n (log n) (log log n))$ битовых операций с требуемым объемом памяти $O (n)$ . ^[15]

Обычно реализованная сегментированная версия страницы имеет ту же операционную сложность $O (n log log n)$ , что и несегментированная версия, но снижает требования к пространству до очень минимального размера страницы сегмента плюс память, необходимая для хранения базовых простых чисел меньше, чем квадратный корень из диапазона, используемого для отбора составных частей из последовательных сегментов страницы размером $O ( .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}√ п / журнал п )$ .

Специальная (редко реализуемая) сегментированная версия решета Эратосфена с базовыми оптимизациями использует $O (n)$ операций и $O (\sqrt n log log n / log n)$ биты памяти. ^[16]^[17]^[18]

Использование большого обозначения O игнорирует постоянные коэффициенты и смещения, которые могут быть очень существенными для практических диапазонов: сито варианта Эратосфена, известное как колесное сито Притчарда. ^[16]^[17]^[18]имеет $производительность O (n)$ , но его базовая реализация требует либо алгоритма «одного большого массива», который ограничивает его полезный диапазон объемом доступной памяти, либо его необходимо сегментировать по страницам, чтобы уменьшить использование памяти. При реализации с сегментацией страниц в целях экономии памяти базовый алгоритм по-прежнему требует около $O (n / log n)$ бит памяти (намного больше, чем требуется базовому сегментированному решету Эратосфена с использованием $O (\sqrt n / log n)$ бит памяти). Работа Причарда снизила требования к памяти за счет большого постоянного коэффициента. Хотя полученное колесное сито имеет $производительность O (n)$ и приемлемые требования к памяти, оно не быстрее, чем базовое сито Эратосфена с разумным коэффициентом колес для практических диапазонов просеивания.

Решето Эйлера [ править ]

Доказательство Эйлера формулы дзета-произведения содержит версию решета Эратосфена, в котором каждое составное число исключается ровно один раз. ^[9] и замечено То же самое сито было заново открыто Грисом и Мисрой (1978) . ^[19]Оно тоже начинается со списка чисел от 2 до $n$ по порядку. На каждом шаге первый элемент идентифицируется как следующее простое число, умножается на каждый элемент списка (таким образом, начиная с самого себя), а результаты отмечаются в списке для последующего удаления. Затем исходный элемент и отмеченные элементы удаляются из рабочей последовательности, и процесс повторяется:

 [2] (3) 5  7   9   11  13  15  17 19  21  23 25  27  29 31  33  35 37  39  41 43  45  47 49  51  53 55  57  59 61  63  65 67  69  71 73  75  77 79  ...
 [3]    (5) 7     11  13    17 19    23  25     29 31     35  37    41 43    47 49    53  55     59 61     65  67    71 73    77 79  ...
 [4]       (7)    11  13    17 19    23       29 31       37    41 43    47  49     53       59 61       67    71 73     77  79  ...
 [5]             (11) 13    17 19    23       29 31       37    41 43    47       53       59 61       67    71 73       79  ...
 [...]

Здесь пример показан начиная с коэффициентов после первого шага алгоритма. Таким образом, на $k$ -м шаге все оставшиеся кратные $k$ -му простому числу удаляются из списка, который после этого будет содержать только числа, взаимно простые с первыми $k$ простыми числами (ср. факторизация колеса ), так что список начнется со следующего простое число, и все числа в нем ниже квадрата его первого элемента тоже будут простыми.

Таким образом, при генерации ограниченной последовательности простых чисел, когда следующее идентифицированное простое число превышает квадратный корень из верхнего предела, все оставшиеся числа в списке являются простыми. ^[9] В приведенном выше примере это достигается путем определения 11 в качестве следующего простого числа и получения списка всех простых чисел, меньших или равных 80.

Обратите внимание, что числа, которые будут отброшены на шаге, по-прежнему используются при обозначении кратных на этом шаге, например, для кратных 3 это 3 × 3 = 9 , 3 × 5 = 15 , 3 × 7 = 21 , 3 × 9 = 27 , ..., 3 × 15 = 45 , ..., поэтому с этим нужно быть осторожным. ^[9]

См. также [ править ]

Ссылки [ править ]

^ Перейти обратно: ^а ^б ^с Хорсли, преподобный Сэмюэл, FRS, « Κόσκινον Ερατοσθένους или Решето Эратосфена. Отчет о его методе нахождения всех простых чисел», Philosophical Transactions (1683–1775), Vol. 62. (1772), стр. 327–347 .
^ Перейти обратно: ^а ^б ^с ^д О'Нил, Мелисса Э., «Настоящее решето Эратосфена» , Журнал функционального программирования , опубликовано онлайн издательством Cambridge University Press 9 октября 2008 г. doi : 10.1017/S0956796808007004 , стр. 10, 11 (содержит два инкрементных сита в Haskell: основанное на приоритетной очереди О'Нила и основанное на списках Ричарда Берда).
^ Хош, Ричард , изд. (1866), Никомахи Герасени Пифагор «Введение в арифметику», книга II, глава XIII, 3 , Лейпциг: Б. Г. Тойбнер, с. 30
^ Перейти обратно: ^а ^б Никомах из Герасы (1926), Введение в арифметику; переведен на английский Мартином Лютером Кингом; с исследованиями по греческой арифметике Фрэнка Эглстона Роббинса и Луи Чарльза Карпински, глава XIII, 3 , Нью-Йорк: The Macmillan Company, стр. 204
^ Дж. К. Морхед, «Распространение решета Эратосфена на арифметические прогрессии и приложения», Анналы математики, вторая серия 10 : 2 (1909), стр. 88–104 .
^ Клоксин, Уильям Ф., Кристофер С. Меллиш, Программирование на Прологе , 1984, стр. 170. ISBN 3-540-11046-1 .
^ Перейти обратно: ^а ^б Рансимен, Колин (1997). «Функциональная жемчужина: ленивые колесные сита и спирали простых чисел» (PDF) . Журнал функционального программирования . 7 (2): 219–225. дои : 10.1017/S0956796897002670 . S2CID 2422563 .
^ Седжвик, Роберт (1992). Алгоритмы на C++ . Аддисон-Уэсли. ISBN 978-0-201-51059-1 . , п. 16.
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Джонатан Соренсон, Введение в сита простых чисел , Технический отчет по компьютерным наукам № 909, факультет компьютерных наук Университета Висконсин-Мэдисон, 2 января 1990 г. (использование оптимизации, начиная с квадратов и, таким образом, используя только те числа, квадрат которых равен ниже верхнего предела).
^ Крэндалл и Померанс, Простые числа: вычислительная перспектива , второе издание, Springer: 2005, стр. 121–24.
^ Бэйс, Картер; Хадсон, Ричард Х. (1977). «Сегментированное решето Эратосфена и простые числа в арифметической прогрессии до 10». ¹²". BIT . 17 (2): 121–127. doi : 10.1007/BF01932283 . S2CID 122592488 .
^ Дж. Соренсон, «Простое решето псевдоквадратов» , Труды 7-го Международного симпозиума по алгоритмической теории чисел . (АНТС-VII, 2006).
^ Тернер, Дэвид А. Руководство по языку SASL. Тех. представитель CS/75/1. Департамент вычислительных наук, Университет Сент-Эндрюс, 1975 г. ( primes = sieve [2..]; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0). Но см. также Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976 , где мы находим следующее , приписываемое П. Куарендону: primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]; приоритет неясен.
^ Пэн, Т. А. (осень 1985 г.). «Один миллион простых чисел через сито» . БАЙТ . стр. 243–244 . Проверено 19 марта 2016 г.
^ Причард, Пол, «Линейные сита простых чисел: генеалогическое древо», Sci. Вычислить. Программирование 9 :1 (1987), стр. 17–35.
^ Перейти обратно: ^а ^б Пол Притчард, «Сублинейное аддитивное сито для поиска простых чисел», Сообщения ACM 24 (1981), 18–23. МИСТЕР 600730
^ Перейти обратно: ^а ^б Пол Причард, Объяснение колесного сита, Acta Informatica 17 (1982), 477–485. МИСТЕР 685983
^ Перейти обратно: ^а ^б Пол Притчард, «Быстрые компактные сита простых чисел» (среди прочего), Журнал алгоритмов 4 (1983), 332–344. МИСТЕР 729229
^ Грис, Дэвид ; Мисра, Джаядев (декабрь 1978 г.), «Алгоритм линейного сита для поиска простых чисел» (PDF) , Communications of the ACM , 21 (12): 999–1003, doi : 10.1145/359657.359660 , hdl : 1813/6407 , S2CID 11990373 .

Внешние ссылки [ править ]

primesieve — очень быстрое и оптимизированное C/C++ сегментированное решето Эратосфена.
Эратосфен, решето в Математической энциклопедии
Интерактивная страница JavaScript
Решето Эратосфена Джорджа Бека, Демонстрационный проект Вольфрама .
Решето Эратосфена в Хаскеле
Алгоритм «Решето Эратосфена» проиллюстрирован и объяснен. Реализации Java и C++.
Соответствующее сито, написанное на языке ассемблера x86.
Быстрое оптимизированное высокопараллельное сегментированное CUDA Решето Эратосфена на C
SieveOfEratosthenesInManyProgrammingLanguages c2 вики-страница
Искусство простого просеивания Решето Эратосфена на языке C 1998 года с объяснением интересных функций и алгоритмических приемов.

[horsley-1] Перейти обратно: ^а ^б ^с Хорсли, преподобный Сэмюэл, FRS, « Κόσκινον Ερατοσθένους или Решето Эратосфена. Отчет о его методе нахождения всех простых чисел», Philosophical Transactions (1683–1775), Vol. 62. (1772), стр. 327–347 .

[ONeill-2] Перейти обратно: ^а ^б ^с ^д О'Нил, Мелисса Э., «Настоящее решето Эратосфена» , Журнал функционального программирования , опубликовано онлайн издательством Cambridge University Press 9 октября 2008 г. doi : 10.1017/S0956796808007004 , стр. 10, 11 (содержит два инкрементных сита в Haskell: основанное на приоритетной очереди О'Нила и основанное на списках Ричарда Берда).

[nicomachus-3] Хош, Ричард , изд. (1866), Никомахи Герасени Пифагор «Введение в арифметику», книга II, глава XIII, 3 , Лейпциг: Б. Г. Тойбнер, с. 30

[nicomachus1926-4] Перейти обратно: ^а ^б Никомах из Герасы (1926), Введение в арифметику; переведен на английский Мартином Лютером Кингом; с исследованиями по греческой арифметике Фрэнка Эглстона Роббинса и Луи Чарльза Карпински, глава XIII, 3 , Нью-Йорк: The Macmillan Company, стр. 204

[5] Дж. К. Морхед, «Распространение решета Эратосфена на арифметические прогрессии и приложения», Анналы математики, вторая серия 10 : 2 (1909), стр. 88–104 .

[6] Клоксин, Уильям Ф., Кристофер С. Меллиш, Программирование на Прологе , 1984, стр. 170. ISBN 3-540-11046-1 .

[Runciman-7] Перейти обратно: ^а ^б Рансимен, Колин (1997). «Функциональная жемчужина: ленивые колесные сита и спирали простых чисел» (PDF) . Журнал функционального программирования . 7 (2): 219–225. дои : 10.1017/S0956796897002670 . S2CID 2422563 .

[sedgewick-8] Седжвик, Роберт (1992). Алгоритмы на C++ . Аддисон-Уэсли. ISBN 978-0-201-51059-1 . , п. 16.

[intro-9] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Джонатан Соренсон, Введение в сита простых чисел , Технический отчет по компьютерным наукам № 909, факультет компьютерных наук Университета Висконсин-Мэдисон, 2 января 1990 г. (использование оптимизации, начиная с квадратов и, таким образом, используя только те числа, квадрат которых равен ниже верхнего предела).

[10] Крэндалл и Померанс, Простые числа: вычислительная перспектива , второе издание, Springer: 2005, стр. 121–24.

[11] Бэйс, Картер; Хадсон, Ричард Х. (1977). «Сегментированное решето Эратосфена и простые числа в арифметической прогрессии до 10». ¹²". BIT . 17 (2): 121–127. doi : 10.1007/BF01932283 . S2CID 122592488 .

[12] Дж. Соренсон, «Простое решето псевдоквадратов» , Труды 7-го Международного симпозиума по алгоритмической теории чисел . (АНТС-VII, 2006).

[13] Тернер, Дэвид А. Руководство по языку SASL. Тех. представитель CS/75/1. Департамент вычислительных наук, Университет Сент-Эндрюс, 1975 г. ( primes = sieve [2..]; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0). Но см. также Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976 , где мы находим следующее , приписываемое П. Куарендону: primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]; приоритет неясен.

[peng1985fall-14] Пэн, Т. А. (осень 1985 г.). «Один миллион простых чисел через сито» . БАЙТ . стр. 243–244 . Проверено 19 марта 2016 г.

[15] Причард, Пол, «Линейные сита простых чисел: генеалогическое древо», Sci. Вычислить. Программирование 9 :1 (1987), стр. 17–35.

[Pritchard1-16] Перейти обратно: ^а ^б Пол Притчард, «Сублинейное аддитивное сито для поиска простых чисел», Сообщения ACM 24 (1981), 18–23. МИСТЕР 600730

[Pritchard2-17] Перейти обратно: ^а ^б Пол Причард, Объяснение колесного сита, Acta Informatica 17 (1982), 477–485. МИСТЕР 685983

[Pritchard3-18] Перейти обратно: ^а ^б Пол Притчард, «Быстрые компактные сита простых чисел» (среди прочего), Журнал алгоритмов 4 (1983), 332–344. МИСТЕР 729229

[19] Грис, Дэвид ; Мисра, Джаядев (декабрь 1978 г.), «Алгоритм линейного сита для поиска простых чисел» (PDF) , Communications of the ACM , 21 (12): 999–1003, doi : 10.1145/359657.359660 , hdl : 1813/6407 , S2CID 11990373 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

v т Это Теоретико-числовые алгоритмы
Тесты на примитивность	АКС АПРЕЛЬ Бэйли – PSW Эллиптическая кривая Поклингтон Ферма Лукас Лукас-Лемер Лукас-Лемер-Ризель Теорема Прота Пепина Квадратичный Фробениус Соловей-Штрассен Миллер-Рабин
Прайм-генерирующий	Сито Аткина Решето Эратосфена Сито Причарда Решето Сундарама Факторизация колес
Целочисленная факторизация	Непрерывная дробь (CFRAC) Диксона Эллиптическая кривая Ленстры (ECM) Эйлера Ро Полларда п - 1 р + 1 Квадратное сито (QS) Сито общего числового поля (GNFS) Сито специального числового поля (SNFS) Рациональное сито Ферма Квадратные формы Шанкса Пробное подразделение Шора
Умножение	Древний Египет Длинный Карацуба Тум-Кук Улицы Шенхаге Фюрера
Евклидово деление	Двоичный Разбивка на части Фурье Гольдшмидт Ньютон-Рафсон Длинный Короткий СТО
Дискретный логарифм	Бэби-шаг, гигантский шаг Поллард Ро Поллард кенгуру Полиг-Хеллман Индексное исчисление Функциональное поле сита
Наибольший общий делитель	Двоичный евклидов Расширенный евклидов Лемерс
Модульный квадратный корень	Лук Поклингтон Тонелли – Шанкс Берлекамп Кунерт
Другие алгоритмы	Чакравала Ворона Возведение в степень возведением в степень Целочисленный квадратный корень Целочисленное отношение ( LLL ; KZ ) Модульное возведение в степень Сокращение Монтгомери Пучок Система Трахтенберга
Курсивом обозначено, что алгоритм предназначен для чисел специальных форм.