Факторизация колес

Факторизация колес с n=2x3x5=30. В желтых областях штрихов не будет.

Факторизация колеса — это метод генерации последовательности натуральных чисел путем повторного сложения, определяемого количеством первых нескольких простых чисел, так что сгенерированные числа по построению являются взаимно простыми с этими простыми числами.

Описание

Для выбранного числа n (обычно не более 4 или 5 ) первые n простых чисел определяют конкретный способ создания последовательности натуральных чисел, о которых заранее известно, что они взаимно просты с этими простыми числами, т. е. о том, что все они не являются простыми. кратны любому из этих простых чисел.

Таким образом, этот метод можно использовать для улучшения метода пробного деления для факторизации целых чисел , поскольку ни одно из сгенерированных чисел не нужно проверять при пробном делении на эти маленькие простые числа.

Метод пробного деления состоит в последовательном делении числа, подлежащего факторизации, на целые числа в порядке возрастания (2, 3, 4, 5, ...). Общее улучшение состоит в проверке только простых чисел, т.е. 2, 3, 5, 7, 11,... .

При факторизации колеса каждый начинает с небольшого списка чисел, называемого базисом — обычно это несколько первых простых чисел ; затем генерируется список, называемый колесом , из целых чисел, взаимно простых со всеми числами в основе.

Тогда для чисел, полученных «вращением колеса», нужно рассматривать только простые числа, не входящие в основу, в качестве их возможных множителей. Это похоже на то, как если бы эти сгенерированные числа уже были проверены и выяснилось, что они не делятся ни на одно из простых чисел в основе. Это оптимизация, поскольку все эти операции становятся избыточными и вообще не выполняются.

При использовании для поиска простых чисел или просеивания в целом этот метод уменьшает количество чисел-кандидатов, которые следует рассматривать как возможные простые числа. С базисом {2, 3} сокращение составляет 1/3 < 34% всех чисел. Это означает, что 2/3 всех номеров-кандидатов автоматически пропускаются. Более крупные базы еще больше уменьшают эту долю; например, с базисом {2, 3, 5} до 8/30 <27% ; и с базисом {2, 3, 5, 7} до 48/210 <23% .

Однако чем больше колесо, тем больше задействованных вычислительных ресурсов и тем меньше дополнительных улучшений, поэтому это случай быстро уменьшающейся отдачи.

Введение

Натуральные числа от 1 и выше нумеруются путем многократного сложения 1:

1, 2, 3, 4, 5, ...

Рассматриваемые промежутками по два числа каждый, они нумеруются путем многократного сложения 2:

1, 2  ;  3, 4  ;  5, 6  ;  ...

Каждое второе таким образом сгенерированное число будет четным. Таким образом, шансы генерируются повторным добавлением 2:

1  ;  3  ;  5  ;  7  ;  ...

Рассматриваемые промежутки по три числа каждый, они нумеруются путем повторного сложения 2 × 3 = 6:

1, 3, 5  ;  7, 9, 11  ;  ...

Каждое второе число в этих тройках будет кратно 3, поскольку все числа вида 3 + 6k нечетно кратны 3. Таким образом, все числа взаимно просты с первыми двумя простыми числами, т. е. 2 и 3, т. е. 2 × 3 = 6–. взаимно простые числа будут генерироваться путем многократного сложения 6, начиная с {1, 5}:

1, 5  ;  7, 11  ;  13, 17  ;  ...

Одну и ту же последовательность можно создать путем многократного сложения 2 × 3 × 5 = 30, превращая каждые пять последовательных интервалов по два числа в каждом в один объединенный интервал из десяти чисел:

1, 5, 7, 11, 13, 17, 19, 23, 25, 29  ;  31, 35, 37, ...

Из каждых десяти из этих 6-взаимно простых чисел два кратны 5, таким образом, оставшиеся восемь будут 30-взаимно простыми:

1, 7, 11, 13, 17, 19, 23, 29  ;  31, 37, 41, 43, 47, 49, ...

Это, естественно, обобщено.

Выше показаны первые три колеса:

• {1} (содержащий одно число, т. е. (2−1)) с «окружностью» 2 для генерации последовательности 2-взаимно простых чисел, т. е. шансов, путем многократного сложения 2;
• {1, 5} (содержащий два числа, т.е. (2−1) × (3−1)) с «окружностью» 2 × 3 = 6, для генерации последовательности 6-взаимно простых чисел путем многократного сложения 6;
• {1, 7, 11, 13, 17, 19, 23, 29} (содержащие восемь чисел, т.е. (2−1) × (3−1) × (5−1)) с «окружностью» 2 × 3 × 5 = 30, для формирования последовательности 30-взаимно простых чисел путем многократного сложения 30; и т. д.

состоит в том, чтобы превратить номера колеса, как показано выше, в круговой список различий Другое представление этих колес между последовательными числами, а затем создать последовательность, начиная с 1, путем многократного добавления этих приращений одно за другим к последнему сгенерированному числу. на неопределенный срок. Это наиболее близко к метафоре «крутящегося колеса» .

Например, это превращает {1, 7, 11, 13, 17, 19, 23, 29, 31} в {6, 4, 2, 4, 2, 4, 6, 2}, а затем последовательность генерируется как

п =1; п +6=7; п +4=11; п +2=13; п +4=17; п +2=19; п +4=23; п +6=29; п +2=31; п +6=37; п +4=41; п +2=43; и т. д.

Типичный пример

При заданной основе первых нескольких простых чисел {2, 3, 5} «первый поворот» колеса состоит из:

7, 11, 13, 17, 19, 23, 29, 31 .

Второй ход получается добавлением 30, произведения основы, к числам первого хода. Третий ход получается добавлением 30 ко второму ходу и так далее.

Для реализации метода можно отметить, что приращения между двумя последовательными элементами колеса, т.е.

вкл = [4, 2, 4, 2, 4, 6, 2, 6],

остаются неизменными после каждого хода.

Предлагаемая ниже реализация использует вспомогательную функцию div( n , k ), которая проверяет, ли n делится нацело на k , и возвращает true в этом случае и false в противном случае. В этой реализации числом, подлежащим факторизации, является n , и программа возвращает наименьший делитель n – возвращая само n , если оно простое.

if div(n, 2) = true then return 2
if div(n, 3) = true then return 3
if div(n, 5) = true then return 5
k := 7; i := 0
while k * k ≤ n do
    if div(n, k) = true, then return k
    k := k + inc[i]
    if i < 7 then i := i + 1 else i := 0
return n

Чтобы получить полную факторизацию целого числа, вычисление можно продолжить, не перезапуская колесо в начале. Это приводит к следующей программе полной факторизации, в которой функция «add» добавляет свой первый аргумент в конец второго аргумента, который должен быть списком.

factors := [ ]
while div(n, 2) = true do
    factors := add(2, factors)
    n := n / 2
while div(n, 3) = true do
    factors := add(3, factors)
    n := n / 3
while div(n, 5) = true do
    factors := add(5, factors)
    n := n / 5
k := 7; i := 0
while k * k ≤ n do
    if div(n, k) = true then 
        add(k, factors)
        n := n / k
    else
        k := k + inc[i]
        if i < 7 then i := i + 1 else i := 0
if n > 1 then add(n, factors)
return factors

Еще одна презентация

Факторизация колеса используется для создания списков, в основном состоящих из простых чисел , из простой математической формулы и гораздо меньшего списка первых простых чисел. Эти списки затем можно использовать при пробном разделении или ситах . Поскольку не все числа в этих списках являются простыми, это приводит к неэффективным избыточным операциям. Однако сами генераторы требуют очень мало памяти по сравнению с хранением чистого списка простых чисел. Небольшой список начальных простых чисел представляет собой полные параметры алгоритма для генерации оставшейся части списка. Эти генераторы называются колесами . Хотя каждое колесо может генерировать бесконечный список чисел, после определенного момента числа перестают быть в основном простыми.

Этот метод может дополнительно применяться рекурсивно в качестве колесного сита с простыми числами для получения более точных колес. Большую исчерпывающую работу по факторизации колес, ситам, использующим факторизацию колес, и колесным решетам провел Пол Притчард. при разработке ряда различных алгоритмов. Чтобы наглядно представить использование колеса факторизации, можно начать с написания натуральных чисел вокруг кругов, как показано на диаграмме рядом. Число спиц выбирается таким образом, чтобы простые числа имели тенденцию накапливаться в меньшинстве спиц.

Пример графической процедуры

1. Найдите первые несколько простых чисел, которые составят основу колеса факторизации. Они известны или, возможно, определены из предыдущих применений меньших колес факторизации или путем быстрого их обнаружения с помощью Решета Эратосфена .
2. Умножьте основные простые числа, чтобы получить результат n , который представляет собой длину окружности колеса факторизации.
3. Напишите числа от 1 до n в кружке. Это будет самый внутренний круг, представляющий один оборот колеса.
4. Из чисел от 1 до n в самом внутреннем круге вычеркните все кратные базовым простым числам из первого шага, как это было применено в шаге 2. Это исключение составных чисел можно выполнить либо с помощью сита, такого как сито Эратосфена, либо с помощью результат применения меньших колес факторизации.
5. Принимая x за количество записанных на данный момент кругов, продолжайте писать от xn + 1 до xn + n концентрическими кругами вокруг самого внутреннего круга, так что xn + 1 находится в том же положении, что и ( x − 1) n + 1.
6. Повторяйте шаг 5 до тех пор, пока наибольший круг вращения не охватит наибольшее число, которое нужно проверить на простоту.
7. Вычеркните цифру 1.
8. Зачеркните спицы простых чисел, найденные на шаге 1 и примененные на шаге 2, во всех внешних кругах, не вычеркивая простые числа в самом внутреннем круге (в круге 1).
9. Зачеркните спицы всех кратных простых чисел, вычеркнутых из внутреннего круга 1 на шаге 4, так же, как зачеркните спицы основных простых чисел на шаге 8.
10. Остальные числа в колесе в основном являются простыми числами (вместе их называют «относительно простыми»). Используйте другие методы, такие как «Решето Эратосфена» или дальнейшее применение более крупных колес факторизации, чтобы удалить оставшиеся непростые числа.

Пример

Факторизация колес с n =2 × 3=6

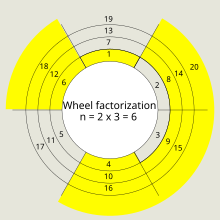
1. Найдите первые два простых числа: 2 и 3.
2. п = 2 × 3 = 6

3. 1  2  3  4  5  6

4. вычеркнуть коэффициенты 2 и 3, которые равны 4 и 6, как коэффициенты 2; 6, поскольку единственный коэффициент 3 уже вычеркнут:

   1  2  3  4  5  6

5. х = 1.
   хп + 1 = 1 ⋅ 6 + 1 = 7.
   ( х + 1) п = (1 + 1) · 6 = 12.
   Напишите от 7 до 12, расположив 7 рядом с 1.

     1  2  3  4  5  6
     7  8  9 10 11 12

6. х = 2.
   хп + 1 = 2 ⋅ 6 + 1 = 13.
   ( х + 1) п = (2 + 1) · 6 = 18.
   Напишите от 13 до 18.
   Повторите эти действия для следующих нескольких строк.

     1  2  3  4  5  6
     7  8  9 10 11 12
    13 14 15 16 17 18
    19 20 21 22 23 24
    25 26 27 28 29 30

7. просеивание

     1  2  3  4  5  6
     7  8  9 10 11 12
    13 14 15 16 17 18
    19 20 21 22 23 24
    25 26 27 28 29 30

8. просеивание

     1  2  3  4  5  6
     7  8  9 10 11 12
    13 14 15 16 17 18
    19 20 21 22 23 24
    25 26 27 28 29 30

9. Полученный список содержит непростое число 25, то есть 5. ² . Используйте другие методы, такие как сито, чтобы устранить его и получить

   2 3 5 7 11 13 17 19 23 29

Обратите внимание, что, используя ровно следующее простое число из 5 циклов колеса и исключив кратные этого простого числа (и только этого простого числа) из полученного списка, мы получили базовое колесо согласно шагу 4 для факторизационного колеса с базой простые числа 2, 3 и 5; это на одно колесо впереди предыдущего колеса факторизации 2/3. Затем можно было бы перейти к шагу 10, используя следующее простое число из 7 циклов и исключая только числа, кратные 7, из полученного списка на шаге 10 (оставив некоторые «относительные» простые числа в этом случае и во всех последующих случаях, т. е. некоторые из них не соответствуют действительности). полностью квалифицированные простые числа), чтобы получить следующее более продвинутое колесо, рекурсивно повторяя шаги по мере необходимости, чтобы получить колеса большего размера.

Анализ и компьютерная реализация

Формально метод использует следующие идеи: во-первых, набор базовых простых чисел, объединенный с его (бесконечным) набором взаимно простых чисел, является надмножеством простых чисел. Во-вторых, бесконечное множество взаимно простых чисел можно легко перечислить от взаимно простых чисел до базового набора между 2 и произведением базового набора. (Обратите внимание, что 1 требует особого обращения.)

Как видно из приведенного выше примера, результатом повторного применения описанной выше рекурсивной процедуры с этапов с 4 по 10 может быть список колес, который охватывает любой желаемый диапазон просеивания (до которого он может быть усечен), и результирующий список тогда включает только кратные значения. простых чисел, превышающих одно после последнего использованного базового простого числа.

Обратите внимание, что как только колесо достигает желаемого верхнего предела диапазона просеивания, можно прекратить создание дальнейших колес и использовать информацию, содержащуюся в этом колесе, для отбраковки оставшихся составных чисел из этого последнего списка колес, используя технику типа Решета Эратосфена, но с использованием зазора. рисунок, присущий кругу, чтобы избежать избыточной отбраковки; некоторые оптимизации могут быть сделаны на основе того факта (будет доказано в следующем разделе), что не будет повторного отбраковки какого-либо составного числа: каждое оставшееся составное число будет отбраковываться ровно один раз. В качестве альтернативы можно продолжать генерировать усеченные списки колес, используя простые числа до квадратного корня из желаемого диапазона сита, и в этом случае все оставшиеся представления чисел в колесе будут простыми; однако, хотя этот метод столь же эффективен, как и отсутствие отбраковки составных чисел более одного раза, он теряет много времени, не связанного с обычно рассматриваемыми операциями отбраковки, при обработке последовательных проходов колеса, поэтому это занимает гораздо больше времени. Исключение составных чисел с помощью колеса факторизации основано на следующем: Учитывая число ⁠ $k>n$⁠ мы знаем, что k не является простым, если k mod n и n не являются взаимно простыми. Отсюда можно определить долю чисел, которую удаляет колесное сито (хотя не все нужно физически вычеркивать; многие из них могут быть отбракованы автоматически в операциях копирования меньших колес на большие) как 1 − φ ( n ) / n , что также является эффективностью сита.

Известно, что

$\lim \inf {\frac {\varphi (n)}{n}}\log \log n=e^{-\gamma }\sim 0.56145948,$

где γ — постоянная Эйлера . Таким образом, phi(n)/n медленно стремится к нулю по мере увеличения n до бесконечности, и можно видеть, что эта эффективность очень медленно возрастает до 100% для бесконечно большого n. Из свойств фи легко увидеть, что наиболее эффективное сито меньше x — это то, на котором $n=p_{1}p_{2}...p_{i}<x$ и $np_{i+1}\geq x$ (т.е. генерация колес может прекратиться, когда последнее колесо пройдет мимо или будет иметь достаточную окружность, чтобы включить наибольшее число в диапазон просеивания).

Чтобы обеспечить максимальное использование на компьютере, нам нужны числа, меньшие n и относительно простые с ним, в виде набора. Используя несколько наблюдений, можно легко создать набор:

1. Начните с $S_{1}=\{1\}$, который является набором для $n=1$ с 2 в качестве первого простого числа. Этот первоначальный набор означает, что все числа, начинающиеся с двойки, включаются как «относительные» простые числа, поскольку длина окружности колеса равна 1.
2. Следующие наборы $S_{2}=\{1\}$ это означает, что он начинается с 3 для всех нечетных чисел с исключенными коэффициентами 2 (окружность 2), $S_{6}=\{1,5\}$ из него исключены коэффициенты 2 и 3 (окружность 6), как для исходного базового колеса в приведенном выше примере, и так далее.
3. Позволять $S_{n}+k$ быть набором, в котором k было добавлено к каждому элементу $S_{n}$.
4. Затем $S_{np_{i+1}}=F_{p_{i+1}}[S_{n}\cup S_{n}+n\cup S_{n}+2n\cup ...\cup S_{n}+n(p_{i+1}-1)]$ где $F_{x}$ представляет собой операцию удаления всех кратных x.
5. 1 и $p_{i+1}$ будут два самых маленьких из $S_{n}$ когда $n>2$ устранение необходимости отдельно вычислять простые числа, хотя алгоритму необходимо вести учет всех исключенных базовых простых чисел, которые больше не включены в последующие наборы.
6. Все наборы, где окружность $n>2$ симметричны вокруг $n/2$, что снижает требования к хранению. Следующий алгоритм не использует этот факт, но он основан на том факте, что промежутки между последовательными числами в каждом наборе симметричны относительно средней точки.

См. также

• Решето Сундарама
• Сито Аткина
• Сито Причарда
• Теория сита

Внешние ссылки

• Факторизация колес
• Улучшенные инкрементные сита простых чисел, разработанные Полом Притчардом.