Алгоритм Шора

Алгоритм Шора — это квантовый алгоритм нахождения простых множителей целого числа. Он был разработан в 1994 году американским математиком Питером Шором . Это один из немногих известных квантовых алгоритмов с убедительными потенциальными приложениями и убедительными доказательствами суперполиномиального ускорения по сравнению с наиболее известными классическими (неквантовыми) алгоритмами. С другой стороны, для факторизации чисел, имеющих практическое значение, требуется гораздо больше кубитов , чем доступно в ближайшем будущем. Другая проблема заключается в том, что шум в квантовых схемах может подорвать результаты. требующие дополнительных кубитов для квантовой коррекции ошибок .

Шор предложил несколько подобных алгоритмов для решения задачи факторизации , задачи дискретного логарифма и задачи нахождения периода. «Алгоритм Шора» обычно относится к алгоритму факторинга, но может относиться к любому из трех алгоритмов. Алгоритм дискретного логарифма и алгоритм факторизации являются экземплярами алгоритма поиска периода, и все три являются экземплярами проблемы скрытой подгруппы .

На квантовом компьютере, чтобы факторизовать целое число $N$Алгоритм Шора работает за полиномиальное время , то есть затраченное время полиномиально $\log N$, где $N$ — размер целого числа, заданного в качестве входных данных. В частности, требуются квантовые вентили порядка $O\!\left((\log N)^{2}(\log \log N)(\log \log \log N)\right)$ используя быстрое умножение, или даже $O\!\left((\log N)^{2}(\log \log N)\right)$ используя асимптотически самый быстрый алгоритм умножения, известный в настоящее время благодаря Харви и Ван Дер Ховену, тем самым демонстрируя, что задача целочисленной факторизации может быть эффективно решена на квантовом компьютере и, следовательно, относится к классу сложности BQP . Это значительно быстрее, чем самый эффективный известный классический алгоритм факторизации, решето общего числового поля , которое работает за субэкспоненциальное время : $O\!\left(e^{1.9(\log N)^{1/3}(\log \log N)^{2/3}}\right)$.

Осуществимость и влияние

Если бы квантовый компьютер с достаточным количеством кубитов мог работать, не поддаваясь квантовому шуму и другим явлениям квантовой декогеренции , то алгоритм Шора можно было бы использовать для взлома схем криптографии с открытым ключом , таких как

• Схема RSA ​
• с конечным полем Диффи-Хеллмана Обмен ключами
• Обмен ключами Диффи-Хеллмана на эллиптической кривой

RSA основан на предположении, что факторизация больших целых чисел вычислительно сложна. Насколько известно, это предположение справедливо для классических (неквантовых) компьютеров; неизвестен ни один классический алгоритм, который мог бы факторизовать целые числа за полиномиальное время. Однако алгоритм Шора показывает, что факторизация целых чисел эффективна на идеальном квантовом компьютере, поэтому может оказаться возможным победить RSA, построив большой квантовый компьютер. Это также послужило мощным стимулом для проектирования и создания квантовых компьютеров, а также для изучения новых алгоритмов квантовых компьютеров. Это также способствовало исследованиям новых криптосистем, защищенных от квантовых компьютеров, которые в совокупности называются постквантовой криптографией .

Физическая реализация

Учитывая высокий уровень ошибок современных квантовых компьютеров и слишком малое количество кубитов для использования квантовой коррекции ошибок , лабораторные демонстрации дают правильные результаты лишь за небольшую часть попыток.

В 2001 году алгоритм Шора был продемонстрирован группой из IBM , которая учла $15$ в $3\times 5$, используя ЯМР-реализацию квантового компьютера с семью кубитами. После внедрения IBM две независимые группы реализовали алгоритм Шора с использованием фотонных многокубитная запутанность . кубитов, подчеркнув, что при запуске схем алгоритма Шора наблюдалась В 2012 году факторизация $15$ было выполнено с использованием твердотельных кубитов. Позже, в 2012 году, факторизация $21$ было достигнуто. В 2016 году факторизация $15$ был выполнен снова с использованием кубитов с захваченными ионами с использованием метода рециркуляции. В 2019 году была предпринята попытка факторизовать количество $35$ используя алгоритм Шора на IBM Q System One , но алгоритм не удался из-за накопления ошибок. Однако во всех этих демонстрациях алгоритм компилировался с использованием предварительного знания ответа, а некоторые даже упрощали алгоритм до такой степени, что он был эквивалентен подбрасыванию монеты. Кроме того, были предприняты попытки использовать квантовые компьютеры с другими алгоритмами. Однако эти алгоритмы подобны классической проверке факторов методом перебора, поэтому, в отличие от алгоритма Шора, от них не ожидается, что они когда-либо будут работать лучше, чем классические алгоритмы факторинга.

Теоретический анализ алгоритма Шора предполагает, что квантовый компьютер свободен от шума и ошибок. Однако в ближайшем будущем практическим реализациям придется иметь дело с такими нежелательными явлениями (когда будет доступно больше кубитов, квантовая коррекция ошибок может помочь). В 2023 году Джин-И Цай показал, что при наличии шума алгоритм Шора асимптотически почти наверняка дает сбой для больших полупростых чисел, которые являются произведениями двух простых чисел в OEIS последовательности A073024 . Эти простые числа $p$ иметь собственность, которая $p-1$ имеет простой делитель больше, чем $p^{2/3}$, и имеют положительную плотность во множестве всех простых чисел. Следовательно, чтобы иметь возможность факторизовать все числа с помощью алгоритма Шора, потребуется коррекция ошибок.

Алгоритм

Проблема, которую мы пытаемся решить: учитывая нечетное составное число $N$, найдите его целые коэффициенты .

Для этого алгоритм Шора состоит из двух частей:

1. Классическое сведение задачи факторинга к задаче нахождения порядка . Это сокращение аналогично тому, которое используется для других алгоритмов факторизации , таких как квадратичное сито .
2. Квантовый алгоритм для решения задачи нахождения порядка.

Классическая редукция

Полный алгоритм факторизации возможен, если мы сможем эффективно факторизовать произвольные $N$ всего на два целых числа $p$ и $q$ больше 1, так как если либо $p$ или $q$ не являются простыми, то алгоритм факторинга, в свою очередь, может быть запущен на них до тех пор, пока не останутся только простые числа.

Основное наблюдение заключается в том, что, используя алгоритм Евклида , мы всегда можем эффективно вычислить НОД между двумя целыми числами. В частности, это означает, что мы можем эффективно проверить, $N$ четно, и в этом случае 2 тривиально является фактором. Предположим, таким образом, что $N$ странно для оставшейся части этой дискуссии. После этого мы можем использовать эффективные классические алгоритмы, чтобы проверить, $N$ это высшая сила . Для степеней простых чисел существуют эффективные классические алгоритмы факторизации: следовательно, остальная часть квантового алгоритма может предполагать, что $N$ не является основной силой.

Если эти простые случаи не приводят к нетривиальному множителю $N$, алгоритм переходит к обработке оставшегося случая. Мы выбираем случайное целое число $2\leq a<N$. Возможный нетривиальный делитель $N$ можно найти, вычислив $\gcd(a,N)$, что можно сделать классически и эффективно с помощью алгоритма Евклида . Если это дает нетривиальный фактор (т.е. $\gcd(a,N)\neq 1$), алгоритм закончен, и есть еще один нетривиальный фактор: ${\textstyle {\frac {N}{\gcd(a,N)}}}$. Если нетривиальный фактор не был выявлен, то это означает, что $N$ и выбор $a$ взаимнопросты поэтому , $a$ содержится в мультипликативной группе целых чисел по модулю $N$, имеющий мультипликативный обратный модуль $N$. Таким образом, $a$ имеет мультипликативный порядок $r$ модуль $N$, значение

$a^{r}\equiv 1{\bmod {N}}$

и $r$ — наименьшее положительное целое число, удовлетворяющее этому сравнению.

Квантовая подпрограмма находит $r$. Из сравнения видно, что $N$ делит $a^{r}-1$, написано $N\mid a^{r}-1$. Это можно факторизовать, используя разность квадратов : $$N\mid (a^{r/2}-1)(a^{r/2}+1)$$ Поскольку мы факторизовали выражение таким образом, алгоритм не работает для нечетных чисел. $r$ (потому что $a^{r/2}$ должно быть целым числом), что означает, что алгоритм придется перезапустить с новым $a$. Поэтому в дальнейшем мы можем предположить $r$ четный. Не может быть так, чтобы $N\mid a^{r/2}-1$, поскольку это означало бы $a^{r/2}\equiv 1{\bmod {N}}$, что противоречиво означало бы, что ${\textstyle {\frac {r}{2}}}$ был бы порядок $a$, что уже было $r$. На данный момент это может быть так, а может и не быть $N\mid a^{r/2}+1$. Если это не правда, что $N\mid a^{r/2}+1$, то это означает, что мы можем найти нетривиальный множитель $N$. Мы вычисляем $$d=\gcd(N,a^{r/2}-1)$$Если $d=1$, то это означает $N\mid a^{r/2}+1$ было правдой, и нетривиальный фактор $N$ не может быть достигнуто из $a$, и алгоритм должен перезапуститься с новым $a$. В противном случае мы нашли нетривиальный множитель $N$, а другое существо ${\textstyle {\frac {N}{d}}}$, и алгоритм закончен. Для этого шага это также эквивалентно вычислению $\gcd(N,a^{r/2}+1)$; это даст нетривиальный фактор, если $\gcd(N,a^{r/2}-1)$ нетривиален и не будет таковым, если он тривиален (где $N\mid a^{r/2}+1$).

Вскоре алгоритм будет сформулирован следующим образом: пусть $N$ быть нечетной, а не простой степенью. Мы хотим вывести два нетривиальных фактора $N$.

1. Выберите случайное число $1<a<N$.
2. Вычислить $K=\gcd(a,N)$, наибольший общий делитель $a$ и $N$.
3. Если $K\neq 1$, затем $K$ является нетривиальным фактором $N$, а другим фактором является ${\textstyle {\frac {N}{K}}}$ и мы закончили.
4. В противном случае используйте квантовую подпрограмму, чтобы найти порядок $r$ из $a$.
5. Если $r$ нечетно, то вернитесь к шагу 1.
6. Вычислить $g=\gcd(N,a^{r/2}+1)$. Если $g$ нетривиален, другой фактор ${\textstyle {\frac {N}{g}}}$, и мы закончили. В противном случае вернитесь к шагу 1.

Было показано, что это, скорее всего, удастся после нескольких запусков. На практике одного вызова подпрограммы поиска квантового порядка достаточно, чтобы полностью факторизовать $N$ с очень высокой вероятностью успеха, если использовать более продвинутую редукцию.

Подпрограмма квантового поиска порядка

Цель квантовой подпрограммы алгоритма Шора состоит в том, чтобы для заданных взаимно простых целых чисел $N$ и $1<a<N$, чтобы найти заказ $r$ из $a$ модуль $N$, которое является наименьшим положительным целым числом таким, что $a^{r}\equiv 1{\pmod {N}}$. Чтобы добиться этого, алгоритм Шора использует квантовую схему, включающую два регистра. Второй регистр использует $n$ кубиты, где $n$ — наименьшее целое число такое, что $N\leq 2^{n}$, то есть, $n=\left\lceil {\log _{2}N}\right\rceil$. Размер первого регистра определяет, насколько точное приближение производит схема. Можно показать, что использование $2n+1$ кубиты дают достаточную точность, чтобы найти $r$. Точная квантовая схема зависит от параметров $a$ и $N$, которые определяют проблему. В следующем описании алгоритма используется обозначение Бракета , а для обозначения квантовых состояний $\otimes$ для обозначения тензорного произведения , а не логического И.

Алгоритм состоит из двух основных шагов:

1. Используйте оценку квантовой фазы с унитарным $U$ представляет собой операцию умножения на $a$ (модуль $N$) и состояние ввода $|0\rangle ^{\otimes 2n+1}\otimes |1\rangle$ (где находится второй регистр $|1\rangle$ сделанный из $n$ кубиты). Собственные значения этого $U$ кодировать информацию о периоде и $|1\rangle$ можно рассматривать как записываемую как сумму собственных векторов. Благодаря этим свойствам этап оценки квантовой фазы выдает на выходе случайное целое число вида ${\frac {j}{r}}2^{2n+1}$ для случайного $j=0,1,...,r-1$.
2. Используйте алгоритм цепных дробей, чтобы извлечь период $r$ по результатам измерений, полученных на предыдущем этапе. Это процедура постобработки (с помощью классического компьютера) данных измерений, полученных в результате измерения выходных квантовых состояний, и извлечения периода.

Связь с квантовой оценкой фазы не обсуждалась в исходной формулировке алгоритма Шора, но позже был предложен Китаевым.

Оценка квантовой фазы

Квантовая подпрограмма в алгоритме Шора

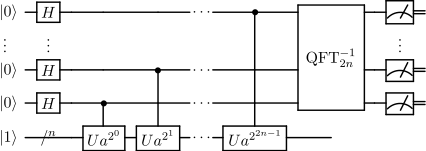
В общем , алгоритм оценки квантовой фазы для любой унитарной $U$ и собственное состояние $|\psi \rangle$ такой, что $U|\psi \rangle =e^{2\pi i\theta }|\psi \rangle$, отправляет состояния ввода $|0\rangle |\psi \rangle$ для вывода состояний, близких к $|\phi \rangle |\psi \rangle$, где $\phi$ целое число, близкое к $2^{2n+1}\theta$. Другими словами, он отправляет каждое собственное состояние $|\psi _{j}\rangle$ из $U$ в состояние, близкое к соответствующему собственному значению. Для целей нахождения квантового порядка мы используем эту стратегию, используя унитарную единицу, определяемую действием $$U|k\rangle ={\begin{cases}|ak{\pmod {N}}\rangle &0\leq k<N,\\|k\rangle &N\leq k<2^{n}.\end{cases}}$$Действие $U$ о штатах $|k\rangle$ с $N\leq k<2^{n}$ не имеет решающего значения для функционирования алгоритма, но его необходимо включить, чтобы гарантировать, что общее преобразование представляет собой четко определенный квантовый вентиль. Реализация схемы оценки квантовой фазы с помощью $U$ требует умения эффективно реализовывать ворота $U^{2^{j}}$. Этого можно добиться с помощью модульного возведения в степень , которое является самой медленной частью алгоритма. Определенные таким образом ворота удовлетворяют $U^{r}=I$, откуда сразу следует, что его собственные значения суть $r$-ые корни единства $\omega _{r}^{k}=e^{2\pi ik/r}$. При этом каждое собственное значение $\omega _{r}^{j}$ имеет собственный вектор вида ${\textstyle |\psi _{j}\rangle =r^{-1/2}\sum _{k=0}^{r-1}\omega _{r}^{-kj}|a^{k}\rangle }$, и эти собственные векторы таковы, что $${\begin{aligned}{\frac {1}{\sqrt {r}}}\sum _{j=0}^{r-1}|\psi _{j}\rangle &={\frac {1}{r}}\sum _{j=0}^{r-1}\sum _{k=0}^{r-1}\omega _{r}^{jk}|a^{k}\rangle \\&=|1\rangle +{\frac {1}{r}}\sum _{k=1}^{r-1}\left(\sum _{j=0}^{r-1}\omega _{r}^{jk}\right)|a^{k}\rangle =|1\rangle ,\end{aligned}}$$

где последнее тождество следует из формулы геометрической прогрессии , откуда следует ${\textstyle \sum _{j=0}^{r-1}\omega _{r}^{jk}=0}$.

Использование квантовой оценки фазы входного состояния $|0\rangle ^{\otimes 2n+1}|\psi _{j}\rangle$ затем вернет целое число $2^{2n+1}j/r$ с высокой вероятностью. Точнее, схема оценки квантовой фазы отправляет $|0\rangle ^{\otimes 2n+1}|\psi _{j}\rangle$ к $|\phi _{j}\rangle |\psi _{j}\rangle$ такое, что результирующее распределение вероятностей $p_{k}\equiv |\langle k|\phi _{j}\rangle |^{2}$ достигает максимума вокруг ${\textstyle k=2^{2n+1}j/r}$, с ${\textstyle p_{2^{2n+1}j/r}\geq {\frac {4}{\pi ^{2}}}\approx 0.4053}$. Эту вероятность можно сделать сколь угодно близкой к 1, используя дополнительные кубиты.

Применение приведенных выше рассуждений к входным данным $|0\rangle ^{\otimes 2n+1}|1\rangle$Таким образом, оценка квантовой фазы приводит к эволюции $$|0\rangle ^{\otimes 2n}|1\rangle ={\frac {1}{\sqrt {r}}}\sum _{j=0}^{r-1}|0\rangle ^{\otimes 2n}|\psi _{j}\rangle \to {\frac {1}{\sqrt {r}}}\sum _{j=0}^{r-1}|\phi _{j}\rangle |\psi _{j}\rangle .$$Измерив первый регистр, мы теперь имеем сбалансированную вероятность $1/r$ найти каждого $|\phi _{j}\rangle$, каждый из которых дает целочисленное приближение к $2^{2n+1}j/r$, который можно разделить на $2^{2n+1}$ чтобы получить десятичное приближение для $j/r$.

Алгоритм непрерывной дроби для получения периода

Затем мы применяем алгоритм цепных дробей для нахождения целых чисел. ${\textstyle b}$ и ${\textstyle c}$, где ${\textstyle {\frac {b}{c}}}$ дает наилучшее приближение дроби для приближения, измеренного по схеме, для ${\textstyle b,c<N}$ и взаимно простые ${\textstyle b}$ и ${\textstyle c}$. Количество кубитов в первом регистре, $2n+1$, определяющий точность аппроксимации, гарантирует, что $${\frac {b}{c}}={\frac {j}{r}}$$с учетом наилучшего приближения из суперпозиции ${\textstyle |\phi _{j}\rangle }$ был измерен (что можно сделать сколь угодно вероятным, используя дополнительные биты и усекая вывод). Однако в то время как ${\textstyle b}$ и ${\textstyle c}$ взаимнопросты, то может быть так, что ${\textstyle j}$ и ${\textstyle r}$ не являются взаимнопростыми. Из-за этого, ${\textstyle b}$ и ${\textstyle c}$ возможно, утратили некоторые факторы, которые были в ${\textstyle j}$ и ${\textstyle r}$. Это можно исправить, перезапустив процедуру поиска квантового порядка произвольное количество раз, чтобы получить список аппроксимаций дробей. $${\frac {b_{1}}{c_{1}}}_{\textstyle ,}\;{\frac {b_{2}}{c_{2}}}_{\textstyle ,}\ldots {\vphantom {\frac {b_{1}}{c_{1}}}}_{\textstyle ,}\;{\frac {b_{s}}{c_{s}}}$$где ${\textstyle s}$ — количество запусков подпрограммы. Каждый ${\textstyle c_{k}}$ из него будут исключены разные коэффициенты, поскольку схема (вероятно) измерит несколько различных возможных значений ${\textstyle j}$. Чтобы восстановить фактическое ${\textstyle r}$ значение, мы можем взять наименьшее общее кратное каждого ${\textstyle c_{k}}$: $$\mathrm {lcm} (c_{1},c_{2},\ldots ,c_{s})$$Наименьшим общим кратным будет порядок ${\textstyle r}$ исходного целого числа ${\textstyle a}$ с высокой вероятностью. На практике одного запуска подпрограммы поиска квантового порядка обычно бывает достаточно, если используется более совершенная постобработка.

Выбор размера первого регистра

Оценка фазы требует выбора размера первого регистра для определения точности алгоритма, а для квантовой подпрограммы алгоритма Шора $2n+1$ кубитов достаточно, чтобы гарантировать, что оптимальная битовая строка, измеренная на основе оценки фазы (то есть $|k\rangle$ где ${\textstyle k/2^{2n+1}}$ является наиболее точной аппроксимацией фазы на основе оценки фазы) позволит получить фактическое значение $r$ быть восстановлены.

Каждый $|\phi _{j}\rangle$ перед измерением в алгоритме Шора представляет собой суперпозицию целых чисел, приближающих $2^{2n+1}j/r$. Позволять $|k\rangle$ представляют наиболее оптимальное целое число в $|\phi _{j}\rangle$. Следующая теорема гарантирует, что алгоритм цепных дробей восстановит $j/r$ от $k/2^{2{n}+1}$:

Теорема — Если $j$ и $r$ являются $n$ битовые целые числа и $$\left\vert {\frac {j}{r}}-\phi \right\vert \leq {\frac {1}{2r^{2}}}$$ тогда алгоритм цепных дробей запускается $\phi$ восстановит оба ${\textstyle {\frac {j}{\gcd(j,\;r)}}}$ и ${\textstyle {\frac {r}{\gcd(j,\;r)}}}$.

Как $k$ — оптимальная битовая строка, полученная из оценки фазы, $k/2^{2{n}+1}$ является точным для $j/r$ к $2n+1$ биты. Таким образом, $$\left\vert {\frac {j}{r}}-{\frac {k}{2^{2n+1}}}\right\vert \leq {\frac {1}{2^{2{n}+1}}}\leq {\frac {1}{2N^{2}}}\leq {\frac {1}{2r^{2}}}$$что означает, что алгоритм цепных дробей восстановит $j$ и $r$ (или выкинув их наибольший общий делитель).

Узкое место

Узким местом времени выполнения алгоритма Шора является квантовое модульное возведение в степень , которое намного медленнее, чем квантовое преобразование Фурье и классическая пред-/пост-обработка. Существует несколько подходов к построению и оптимизации схем модульного возведения в степень. Самый простой и (на данный момент) наиболее практичный подход — имитировать обычные арифметические схемы с обратимыми вентилями , начиная с сумматоров с пульсирующим переносом . Знание базы и модуля возведения в степень облегчает дальнейшую оптимизацию. Реверсивные схемы обычно используют порядка $n^{3}$ ворота для $n$ кубиты. Альтернативные методы асимптотически улучшают количество вентилей за счет использования квантовых преобразований Фурье , но не могут конкурировать с кубитами менее 600 из-за высоких констант.

Нахождение периода и дискретные логарифмы

Алгоритмы Шора для дискретного логарифма и задач нахождения порядка являются примерами алгоритма, решающего задачу нахождения периода. . Все три являются примерами проблемы скрытой подгруппы .

Алгоритм Шора для дискретных логарифмов

Учитывая группу $G$ с заказом $p$ и генератор $g\in G$, предположим, мы это знаем $x=g^{r}\in G$, для некоторых $r\in \mathbb {Z} _{p}$, и мы хотим вычислить $r$, что является дискретным логарифмом : $r={\log _{g}}(x)$. Рассмотрим абелеву группу $\mathbb {Z} _{p}\times \mathbb {Z} _{p}$, где каждый фактор соответствует модульному сложению значений. Теперь рассмотрим функцию

$f\colon \mathbb {Z} _{p}\times \mathbb {Z} _{p}\to G\;;\;f(a,b)=g^{a}x^{-b}.$

Это дает нам абелеву задачу о скрытой подгруппе , где $f$ соответствует групповому гомоморфизму . Ядро соответствует кратным $(r,1)$. Итак, если мы сможем найти ядро, мы сможем найти $r$. Квантовый алгоритм решения этой проблемы существует. Этот алгоритм, как и алгоритм поиска коэффициентов, принадлежит Питеру Шору, и оба они реализованы путем создания суперпозиции с использованием вентилей Адамара с последующей реализацией $f$ как квантовое преобразование, за которым, наконец, следует квантовое преобразование Фурье. В связи с этим квантовый алгоритм вычисления дискретного логарифма также иногда называют «алгоритмом Шора».

Проблему поиска порядка можно также рассматривать как проблему скрытой подгруппы. Чтобы убедиться в этом, рассмотрим сложенную группу целых чисел и для заданного $a\in \mathbb {Z}$ такой, что: $a^{r}=1$, функция

$f\colon \mathbb {Z} \to \mathbb {Z} \;;\;f(x)=a^{x},\;f(x+r)=f(x).$

Для любой конечной абелевой группы $G$, существует квантовый алгоритм для решения скрытой подгруппы для $G$ за полиномиальное время.

См. также

• GEECM , алгоритм факторизации, который, как говорят, «часто намного быстрее, чем алгоритм Шора».
• Алгоритм Гровера

Дальнейшее чтение

• Нильсен, Майкл А.; Чуанг, Исаак Л. (2010). Квантовые вычисления и квантовая информация: издание к 10-летию . Издательство Кембриджского университета. ISBN  978-1-107-00217-3 .
• Кэй, Филипп; Лафламм, Раймонд; Моска, Мишель (2006). Введение в квантовые вычисления . дои : 10.1093/oso/9780198570004.001.0001 . ISBN  978-0-19-857000-4 .
• «Объяснение для обывателя» Скотта Ааронсона , « одобренное » Питером Шором. (Шор написал: «Отличная статья, Скотт! Это лучшая работа по объяснению квантовых вычислений обывателю, которую я когда-либо видел»). Альтернативная метафора QFT была представлена ​​в одном из комментариев . Скотт Ааронсон предлагает для дальнейшего чтения следующие 12 ссылок (из «10 ^{10 5000} учебные пособия по квантовым алгоритмам, которые уже есть в сети."):
• Шор, Питер В. (1997), «Алгоритмы полиномиального времени для факторизации простых чисел и дискретных логарифмов на квантовом компьютере», SIAM J. Comput. , 26 (5): 1484–1509, arXiv : quant-ph/9508027v2 , Bibcode : 1999SIAMR..41..303S , doi : 10.1137/S0036144598347011 . Пересмотренная версия оригинальной статьи Питера Шора («28 страниц, LaTeX. Это расширенная версия статьи, опубликованной в Трудах 35-го ежегодного симпозиума по основам компьютерных наук, Санта-Фе, Нью-Мексико, 20 ноября — 22, 1994. Незначительные изменения внесены в январе 1996 г.»).
• Квантовые вычисления и алгоритм Шора Мэтью Хейворда , Страница квантовых алгоритмов , 17 февраля 2005 г., imsa.edu, LaTeX2HTML-версия исходного документа LaTeX , также доступна в формате PDF или Postscript .
• Квантовые вычисления и алгоритм факторизации Шора , Рональд де Вольф, CWI и Амстердамский университет, 12 января 1999 г., 9-страничный постскриптум.
• Алгоритм факторинга Шора , Заметки из лекции 9 Беркли CS 294–2 от 4 октября 2004 г., 7-страничный постскриптум.
• Глава 6 «Квантовые вычисления». Архивировано 30 апреля 2020 г. в Wayback Machine , 91-страничный постскриптум, Калифорнийский технологический институт, Preskill, PH229.
• Квантовые вычисления: учебник Сэмюэля Л. Браунштейна .
• Квантовые состояния алгоритма Шора , Нил Янг, последнее изменение: вторник, 21 мая, 11:47:38 1996 г.
• III. Взлом шифрования RSA с помощью квантового компьютера: алгоритм факторизации Шора , конспекты лекций по квантовым вычислениям, Корнельский университет, физика 481–681, CS 483; Весна 2006 г., Н. Дэвид Мермин. Последняя редакция 28 марта 2006 г., 30-страничный PDF-документ.
• Лавор, К.; Мансур, ЛРУ; Португалия, Р. (2003). «Алгоритм Шора для факторизации больших целых чисел». arXiv : Quant-ph/0303175 .
• Ломонако-младший (2000). «Алгоритм квантового факторинга Шора». arXiv : Quant-ph/0010034 . Эта статья представляет собой письменную версию часовой лекции, посвященной алгоритму квантового факторинга Питера Шора. 22 страницы.
• Глава 20 «Квантовые вычисления» , из книги «Вычислительная сложность: современный подход» , черновик книги: датировано январем 2007 г., Санджив Арора и Боаз Барак, Принстонский университет. Опубликовано в главе 10 «Квантовые вычисления» Санджив Арора, Боаз Барак, «Сложность вычислений: современный подход», Cambridge University Press, 2009 г., ISBN   978-0-521-42426-4
• Шаг к квантовым вычислениям: запутанность 10 миллиардов частиц. Архивировано 20 января 2011 г. в Wayback Machine из журнала Discover Magazine от 19 января 2011 г.
• Йозеф Груска - Проблемы квантовых вычислений также в неограниченной математике: 2001 г. и далее , редакторы Бьёрн Энгквист, Вильфрид Шмид, Springer, 2001 г., ISBN   978-3-540-66913-5

Внешние ссылки

• Версия 1.0.0 libquantum : содержит реализацию алгоритма Шора на языке C с их библиотекой моделирования квантовых компьютеров, но переменная ширины в shor.c должна быть установлена ​​на 1, чтобы повысить сложность выполнения.
• PBS Infinite Series создала два видеоролика, объясняющих математические принципы алгоритма Шора: « Как взломать криптографию » и « Взлом на квантовой скорости с помощью алгоритма Шора ».
• Полная реализация алгоритма Шора с помощью Classiq