Сверхпроводящие квантовые вычисления

Сверхпроводящие квантовые вычисления — это отрасль твердотельных квантовых вычислений, в которой реализуются сверхпроводящие электронные схемы , использующие сверхпроводящие кубиты в качестве искусственных атомов или квантовых точек . Для сверхпроводящих кубитов два логических состояния — это основное состояние и возбужденное состояние , обозначаемые $|g\rangle {\text{ and }}|e\rangle$соответственно. Исследования в области сверхпроводящих квантовых вычислений проводят такие компании, как Google , ИБМ , ИМЭК , ББН Технологии , Сбрасывает , и Интел . Многие недавно разработанные QPU ( квантовые процессоры или квантовые чипы) используют сверхпроводящую архитектуру.

По состоянию на май 2016 г. до 9 полностью управляемых кубитов демонстрируется в 1D массиве , и до 16 в 2D-архитектуре. В октябре 2019 года группа Мартиниса в партнерстве с Google опубликовала статью, демонстрирующую новое квантовое превосходство с использованием чипа, состоящего из 53 сверхпроводящих кубитов.

Предыстория

Классические вычислительные модели опираются на физические реализации, соответствующие законам классической механики . Классические описания точны только для конкретных систем, состоящих из относительно большого числа атомов. Более общее описание природы даёт квантовая механика . Квантовые вычисления изучают приложения квантовых явлений, выходящие за рамки классического приближения, с целью выполнения квантовой обработки и передачи информации. Существуют различные модели квантовых вычислений, но наиболее популярные модели включают концепции кубитов и квантовых вентилей (или сверхпроводящих квантовых вычислений на основе вентилей).

Сверхпроводники реализуются благодаря тому, что при низких температурах они имеют бесконечную проводимость и нулевое сопротивление. Каждый кубит построен с использованием полупроводниковых схем с LC-цепью : конденсатора и катушки индуктивности.

Сверхпроводящие конденсаторы и катушки индуктивности используются для создания резонансного контура, который почти не рассеивает энергию, поскольку тепло может нарушить квантовую информацию. Сверхпроводящие резонансные контуры представляют собой класс искусственных атомов, которые можно использовать в качестве кубитов. Теоретические и физические реализации квантовых схем сильно различаются. Реализация квантовой схемы имела свои собственные проблемы и должна соответствовать критериям ДиВинченцо , условиям, предложенным физиком-теоретиком Дэвидом П. ДиВинченцо. который представляет собой набор критериев для физической реализации сверхпроводящих квантовых вычислений, где первоначальные пять критериев гарантируют, что квантовый компьютер соответствует постулатам квантовой механики, а остальные два относятся к передаче этой информации по сети.

Мы сопоставляем основное и возбужденное состояния этих атомов с состояниями 0 и 1, поскольку это дискретные и разные значения энергии, и, следовательно, это соответствует постулатам квантовой механики. Однако в такой конструкции электрон может переходить во множество других энергетических состояний и не ограничиваться нашим возбужденным состоянием; поэтому крайне важно, чтобы на систему воздействовали только фотоны с разницей в энергии, необходимой для перехода из основного состояния в возбужденное состояние. Однако при этом остается одна серьезная проблема: нам требуется неравномерное расстояние между нашими энергетическими уровнями, чтобы фотоны с одинаковой энергией не вызывали переходы между соседними парами состояний. Джозефсоновские переходы представляют собой сверхпроводящие элементы с нелинейной индуктивностью, что критически важно для реализации кубитов. Использование этого нелинейного элемента в резонансной сверхпроводящей цепи приводит к неравномерности расстояний между энергетическими уровнями.

Кубиты

Кубит — это обобщение бита ( системы с двумя возможными состояниями ), способного занимать квантовую суперпозицию обоих состояний. С другой стороны, квантовый вентиль — это обобщение логического вентиля, описывающее преобразование одного или нескольких кубитов после применения вентиля с учетом их начального состояния. Физическая реализация кубитов и вентилей является сложной задачей по той же причине, по которой квантовые явления трудно наблюдать в повседневной жизни, учитывая мельчайшие масштабы, в которых они происходят. Одним из подходов к созданию квантовых компьютеров является внедрение сверхпроводников , благодаря которым квантовые эффекты становятся макроскопически наблюдаемыми, хотя и ценой чрезвычайно низких рабочих температур .

Сверхпроводники

В отличие от типичных проводников, сверхпроводники обладают критической температурой , при которой удельное сопротивление падает почти до нуля, а проводимость резко возрастает. В сверхпроводниках основными носителями заряда являются пары электронов (известные как куперовские пары ), а не одиночные фермионы , как в типичных проводниках. Куперовы пары слабосвязаны и имеют энергетическое состояние ниже, чем у энергии Ферми . Электроны, образующие куперовские пары, обладают равным и противоположным импульсом и спином, так что общий спин куперовской пары является целым числом . Следовательно, куперовские пары являются бозонами . Двумя такими сверхпроводниками, которые использовались в моделях сверхпроводящих кубитов, являются ниобий и тантал , оба сверхпроводники d-диапазона.

Конденсаты Бозе-Эйнштейна

После охлаждения почти до абсолютного нуля группа бозонов коллапсирует в квантовое состояние с самой низкой энергией ( основное состояние ), образуя состояние материи, известное как конденсат Бозе-Эйнштейна . В отличие от фермионов, бозоны могут занимать один и тот же квантовый энергетический уровень (или квантовое состояние ) и не подчиняться принципу запрета Паули . Классически конденсат Бозе-Эйнштейна можно представить как множество частиц, занимающих одно и то же положение в пространстве и имеющих равный импульс . Поскольку силы взаимодействия между бозонами сведены к минимуму, конденсаты Бозе-Эйнштейна эффективно действуют как сверхпроводники. Таким образом, сверхпроводники используются в квантовых вычислениях, поскольку они обладают как почти бесконечной проводимостью , так и почти нулевым сопротивлением . Таким образом, преимущества сверхпроводника перед обычным проводником двояки: теоретически сверхпроводники могут передавать сигналы почти мгновенно и работать бесконечно без потерь энергии. Перспектива создания сверхпроводящих квантовых компьютеров становится еще более многообещающей, учитывая НАСА Недавнее развитие лаборатории холодного атома в космическом пространстве, где конденсаты Бозе-Эйнштейна легче получить и поддерживать (без быстрого рассеяния) в течение более длительных периодов времени без ограничений гравитации .

Электрические схемы

В каждой точке сверхпроводящей электронной схемы (сети электрических элементов конденсата, ) волновая функция описывающая поток заряда , четко определяется некоторой комплексной амплитудой вероятности . В типичных электрических цепях с проводниками то же самое описание справедливо для отдельных носителей заряда, за исключением того, что различные волновые функции усредняются при макроскопическом анализе, что делает невозможным наблюдение квантовых эффектов. конденсата Волновая функция становится полезной для разработки и измерения макроскопических квантовых эффектов. Подобно дискретным уровням атомной энергии в модели Бора , только дискретное количество квантов магнитного потока может проникнуть в сверхпроводящую петлю. В обоих случаях квантование является результатом комплексной амплитуды непрерывности . В отличие от микроскопических реализаций квантовых компьютеров (таких как атомы или фотоны ), параметры сверхпроводящих цепей разрабатываются путем задания (классических) значений составляющих их электрических элементов, например, путем регулировки емкости. или индуктивность .

Чтобы получить квантовомеханическое описание электрической цепи, необходимо выполнить несколько шагов. Во-первых, все электрические элементы должны описываться амплитудой и фазой волновой функции конденсата, а не тесно связанными макроскопическими описаниями тока и напряжения , используемыми для классических схем. Например, квадрат амплитуды волновой функции в любой произвольной точке пространства соответствует вероятности найти там носитель заряда. Следовательно, квадрат амплитуды соответствует классическому распределению заряда. Второе требование для получения квантовомеханического описания электрической цепи заключается в том, что обобщенные законы цепи Кирхгофа системы применяются в каждом узле электрической цепи для получения уравнений движения . Наконец, эти уравнения движения необходимо переформулировать в лагранжевой механике так, чтобы получить квантовый гамильтониан, описывающий полную энергию системы.

Технология

Производство

Сверхпроводящие квантовые вычислительные устройства обычно разрабатываются в радиочастотном диапазоне , охлаждаются в холодильниках разбавления ниже 15 мК и обрабатываются обычными электронными приборами, например, синтезаторами частот и анализаторами спектра . Типичные размеры находятся в диапазоне микрометров с разрешением субмикрометра, что позволяет удобно проектировать гамильтонову систему с использованием хорошо зарекомендовавшей себя технологии интегральных схем . Производство сверхпроводящих кубитов следует процессу, включающему литографию , осаждение металла, травление и контролируемое окисление , как описано в . Производители продолжают увеличивать срок службы сверхпроводящих кубитов и с начала 2000-х годов добились значительных улучшений.

Джозефсоновские переходы

Одиночный джозефсоновский переход, где C — тонкий слой изолятора, а A и B — (сверхпроводящие) токи с неэквивалентными волновыми функциями.

Одной из отличительных особенностей сверхпроводящих квантовых схем является использование джозефсоновских переходов . Джозефсоновские переходы представляют собой электрический элемент , которого нет в обычных проводниках . Напомним, что переход — это слабое соединение между двумя выводами провода (в данном случае сверхпроводящего провода) по обе стороны от тонкого слоя изоляционного материала толщиной всего в несколько атомов , обычно реализуемого с использованием теневого испарения метода . Полученное устройство с джозефсоновским переходом демонстрирует эффект Джозефсона , при котором переход создает сверхток . Справа показано изображение одиночного джозефсоновского перехода. Волновая функция конденсата на двух сторонах перехода слабо коррелирует, а это означает, что им разрешено иметь разные сверхпроводящие фазы. Это различие в нелинейности контрастирует с непрерывным сверхпроводящим проводом, для которого волновая функция на переходе должна быть непрерывной . Течение тока через переход происходит посредством квантового туннелирования , которое, кажется, мгновенно «туннелирует» от одной стороны перехода к другой. Это явление туннелирования уникально для квантовых систем. Таким образом, квантовое туннелирование используется для создания нелинейной индуктивности, необходимой для проектирования кубитов, поскольку оно позволяет создавать ангармонические осцилляторы , для которых уровни энергии дискретизированы (или квантованы ) с неравномерным расстоянием между уровнями энергии, обозначаются $\Delta E$. Напротив, квантовый гармонический осциллятор не может использоваться в качестве кубита, поскольку невозможно обратиться только к двум его состояниям, учитывая, что расстояние между каждым энергетическим уровнем и следующим абсолютно одинаково.

Архетипы кубитов

Три основных архетипа сверхпроводящих кубитов — это фазовый , зарядовый и потоковой кубиты. Существует множество гибридизаций этих архетипов, включая флюксоний, трансмон , Хмон, и квантроний. Для любой реализации кубита логические квантовые состояния $\{|0\rangle ,|1\rangle \}$ отображаются уровни в различные состояния физической системы (обычно в дискретные энергии или их квантовые суперпозиции ). Каждый из трех архетипов обладает определенным диапазоном соотношения энергии Джозефсона к энергии заряда. Энергия Джозефсона относится к энергии, запасенной в джозефсоновских переходах при прохождении тока, а энергия зарядки — это энергия, необходимая одной куперовской паре для зарядки полной емкости перехода. Энергию Джозефсона можно записать как

График различных архетипов сверхпроводящих кубитов по соотношению их энергии Джозефсона к энергии заряда с легендой справа. На верхнем левом рисунке изображена унимонная электрическая цепь.

$U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}\cos \delta$,

где $I_{0}$ – критический параметр тока джозефсоновского перехода, $\Phi _{0}={\frac {h}{2e}}$ (сверхпроводящий) квант потока , и $\delta$ - это разность фаз на переходе. Обратите внимание, что термин $cos\delta$ указывает на нелинейность джозефсоновского перехода. Энергия заряда записывается как

$E_{C}={\frac {e^{2}}{2C}}$,

где $C$ - емкость перехода и $e$ является зарядом электрона. Из трех архетипов фазовые кубиты позволяют большинству куперовских пар туннелировать через переход, за ними следуют потоковые кубиты, а зарядовые кубиты позволяют наименьшему количеству.

Фазовый кубит

Фазовый кубит обладает отношением джозефсоновской энергии к энергии заряда порядка величины $10^{6}$. Для фазовых кубитов уровни энергии соответствуют различным амплитудам колебаний квантового заряда на джозефсоновском переходе, где заряд и фаза аналогичны импульсу и положению соответственно, как аналогично квантовому гармоническому осциллятору . Обратите внимание, что в этом контексте фаза является комплексным аргументом сверхпроводящей волновой функции (также известной как параметр порядка сверхпроводимости ), а не фазой между различными состояниями кубита.

На крайнем левом изображении показана сверхпроводящая петля флуксония, состоящая из набора джозефсоновских переходов большей площади и одного джозефсоновского перехода меньшей площади, как показано с помощью электронного микроскопа. На верхнем правом изображении показаны компоненты флюксониевой схемы, а на нижнем правом изображении — джозефсоновский переход меньшей площади.

Поток кубита

Кубит потока (также известный как кубит постоянного тока) обладает отношением джозефсоновской энергии к энергии заряда порядка величины. $10$. Для кубитов потока уровни энергии соответствуют разным целым числам квантов магнитного потока, захваченных в сверхпроводящее кольцо.

Флюксоний

Флюксониевые кубиты представляют собой особый тип потокового кубита, джозефсоновский переход которого шунтируется линейным индуктором $E_{J}\gg E_{L}$ где $E_{L}=(\hbar /2e)^{2}/L$. На практике линейный индуктор обычно реализуется в виде массива джозефсоновских переходов, состоящего из большого количества (часто может быть $N>100$) крупногабаритных джозефсоновских переходов, соединенных последовательно. При этом условии гамильтониан флюксония можно записать как:

${\hat {H}}=4E_{C}{\hat {n}}^{2}+{\frac {1}{2}}E_{L}({\hat {\phi }}-\phi _{\mathrm {ext} })^{2}-E_{J}\cos {\hat {\phi }}$.

Одним из важных свойств кубита-флюксония является более длительное время жизни кубита в зоне наилучшего восприятия половинного потока, которое может превышать 1 миллисекунду. Еще одним решающим преимуществом смещения флюксониевого кубита в наилучшей зоне является большая ангармоничность, которая позволяет быстро локально управлять микроволновым излучением и смягчает проблемы спектральной скученности, что приводит к лучшей масштабируемости.

Зарядный кубит

Зарядовый кубит, также известный как ящик куперовской пары , имеет отношение джозефсоновской энергии к энергии заряда порядка величины. $<1$. Для зарядовых кубитов различные уровни энергии соответствуют целому числу куперовских пар на сверхпроводящем острове (небольшой сверхпроводящей области с контролируемым количеством носителей заряда). Действительно, первым экспериментально реализованным кубитом стал ящик пар Купера, созданный в 1999 году.

Устройство, состоящее из четырех сверхпроводящих трансмонных кубитов, четырех квантовых шин и четырех считывающих резонаторов , изготовленное IBM и опубликованное в журнале npj Quantum Information в январе 2017 года.

Трансмон

Трансмоны — это особый тип кубита с шунтирующим конденсатором, специально предназначенным для подавления шума . Модель трансмонного кубита была основана на парном ящике Купера. (показано в таблице выше в первой строке, первом столбце). Это был также первый кубит, продемонстрировавший квантовое превосходство . Увеличенное отношение джозефсоновской энергии к энергии заряда снижает шум. Два трансмона можно соединить с помощью разделительного конденсатора . Для этой двухкубитной системы гамильтониан записывается

${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$,

где $J$ и тока плотность $\sigma$ - поверхностная плотность заряда .

Хмон

Xmon по конструкции очень похож на трансмон, поскольку он создан на основе планарной модели трансмона. Xmon — это, по сути, настраиваемый трансмон. Основное различие между кубитами Transmon и Xmon заключается в том, что кубиты Xmon заземлены с помощью одной из площадок конденсатора.

Гейтмон

Другой вариант трансмонного кубита — Gatemon. Как и Xmon, Gatemon представляет собой настраиваемую вариацию трансмона. Gatemon настраивается с помощью напряжения на затворе .

Сверхпроводящая схема, состоящая из трех Unimons (синих), каждый из которых подключен к резонаторам (красный), линиям привода (зеленый) и линиям совместных зондов (желтый).

Унимон

В 2022 году исследователи из IQM Quantum Computers, Университета Аалто и Центра технических исследований VTT в Финляндии обнаружили новый сверхпроводящий кубит, известный как Unimon. Относительно простой кубит, Unimon состоит из одного джозефсоновского перехода, шунтированного линейным индуктором (обладающим индуктивностью, не зависящей от тока) внутри (сверхпроводящего) резонатора . Unimons обладают повышенной ангармоничностью и обеспечивают более быстрое время работы, что приводит к снижению восприимчивости к шумовым ошибкам. Помимо повышенной ангармоничности, другие преимущества кубита Unimon включают пониженную восприимчивость к шуму потока и полную нечувствительность к шуму заряда постоянного тока.

Архетипы сверхпроводящих кубитов

Тип Аспект	Зарядный кубит	RF-SQUID-кубит (прототип Flux-кубита)	Фазовый кубит
Схема	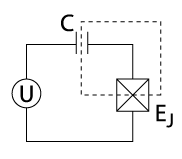Схема зарядного кубита. определен между выводами конденсатора емкостью Сверхпроводящий остров (обведен пунктирной линией ) $C$ и джозефсоновский переход с энергией $E_{J}$ смещен напряжением $U$.	Схема потока кубита. Сверхпроводящая петля с индуктивностью $L$ прерывается соединением с энергией Джозефсона $E_{J}$. Поток смещения $\Phi$ индуцируется линией потока с током $I_{0}$.	Схема фазового кубита. Джозефсоновский переход с энергетическим параметром $E_{J}$ смещается под действием тока $I_{0}$.
гамильтониан	$H=E_{C}(N-N_{g})^{2}-E_{J}\cos \phi$ В этом случае $N$ - количество куперовских пар, которые прокладывают туннель через соединение, $N_{g}=CV_{0}/2e$ – заряд конденсатора в единицах числа куперовских пар, $E_{C}=(2e)^{2}/2(C_{J}+C)$ - энергия заряда, связанная с обеими емкостью $C$ и емкость джозефсоновского перехода $C_{J}$.	$H={\frac {q^{2}}{2C_{J}}}+\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]$ Обратите внимание, что $\phi$ разрешено принимать только значения, превышающие $2\pi$ и альтернативно определяется как интеграл по времени от напряжения по индуктивности $L$.	$H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$Здесь $\Phi _{0}$ – квант магнитного потока.
Потенциал	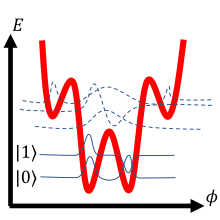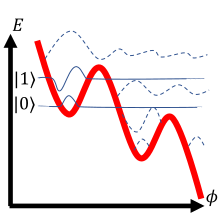$U=-E_{J}\cos \phi$ . Напряжение смещения устанавливается таким, что $N_{g}={\frac {1}{2}}$, минимизируя энергетический разрыв между $|0\rangle$ и $|1\rangle$, что позволяет отличить этот разрыв от других энергетических разрывов (например, разрыва между $|1\rangle$ и $|2\rangle$). Разница в пробелах позволяет решить проблему перехода от $|0\rangle$ к $|1\rangle$ и только наоборот, без заселения других государств.	$U=\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]$ Поток смещения ​ $\Phi =\Phi _{0}/2$. Разным ямам соответствует разное количество квантов потока, захваченных в сверхпроводящих петлях. Два нижних состояния соответствуют симметричной и антисимметричной суперпозиции нулевых или одиночных захваченных квантов потока, иногда обозначаемых как состояния контурного тока по часовой стрелке и против часовой стрелки: $|0\rangle =\left[|\circlearrowleft \rangle +|\circlearrowright \rangle \right]/{\sqrt {2}}$ и $|1\rangle =\left[|\circlearrowleft \rangle -|\circlearrowright \rangle \right]/{\sqrt {2}}$.	$U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$, также известный как потенциал «стиральной доски». Ток смещения регулируется так, чтобы ямы были достаточно мелкими, чтобы содержать ровно две локализованные волновые функции. Небольшое увеличение тока смещения вызывает селективный «выброс» более высокого энергетического состояния ( $|1\rangle$), выражаемый измеримым скачком напряжения (механизм, обычно используемый для измерения фазового кубита ).

В таблице выше рассмотрены три архетипа сверхпроводящих кубитов. В первой строке представлена ​​электрическая схема кубита. Во второй строке изображен квантовый гамильтониан, полученный из схемы. энергии системы Как правило, гамильтониан представляет собой сумму компонентов кинетической и потенциальной (аналог частицы в потенциальной яме ). Для обозначенных гамильтонианов $\phi$ - разность фаз сверхпроводящей волновой функции на переходе, $C_{J}$ - емкость, связанная с джозефсоновским переходом, и $q$ - заряд емкости перехода. Для каждого изображенного потенциала для расчета используются только сплошные волновые функции. Потенциал кубита обозначен толстой красной линией, а схематические решения волновой функции изображены тонкими линиями, поднятыми для ясности до соответствующего энергетического уровня.

Обратите внимание, что масса частицы соответствует обратной функции емкости цепи и что форма потенциала определяется регулярными индукторами и джозефсоновскими переходами. Схематические волновые решения в третьей строке таблицы показывают комплексную амплитуду фазовой переменной. В частности, если фаза кубита измеряется, когда кубит находится в определенном состоянии, существует ненулевая вероятность измерения определенного значения только там, где изображенная волновая функция колеблется. Все три строки представляют собой по существу разные представления одной и той же физической системы.

Одиночные кубиты

Энергетический разрыв в ГГц между энергетическими уровнями сверхпроводящего кубита спроектирован так, чтобы быть совместимым с доступным электронным оборудованием из-за терагерцового разрыва (отсутствия оборудования в более высокочастотном диапазоне ). предполагает Энергетическая щель сверхпроводника верхний предел работы ниже ~ 1 ТГц, за которым происходит разрыв куперовских пар, поэтому разделение энергетических уровней не может быть слишком высоким. С другой стороны, расстояние между уровнями энергии не может быть слишком маленьким из соображений охлаждения: температура 1 К предполагает колебания энергии 20 ГГц. Температуры в десятки милликельвинов достигаются в холодильниках разбавления и позволяют кубитам работать при разнице энергетических уровней ~ 5 ГГц. Разделение уровней энергии кубита часто регулируется путем управления специальной линией тока смещения , предоставляющей «ручку» для точной настройки параметров кубита.

Однокубитные вентили

Изображение сферы Блоха.

Однокубитный вентиль достигается за счет вращения в сфере Блоха . Вращение между различными уровнями энергии одного кубита индуцируется микроволновыми импульсами, посылаемыми на антенну или линию передачи , связанную с кубитом, с частотой, резонансной с энергетическим разделением между уровнями. Отдельные кубиты могут обращаться по выделенной линии передачи или по общей, если другие кубиты не находятся в резонансе . Ось вращения задается квадратурной амплитудной модуляцией СВЧ-импульса, а длина импульса определяет угол поворота .

Более формально (следуя обозначениям ) для сигнала движения

${\mathcal {E}}(t)={\mathcal {E}}^{x}(t)\cos(\omega _{d}t)+{\mathcal {E}}^{y}(t)\sin(\omega _{d}t)$

частоты $\omega _{d}$, гамильтониан ведомого кубита в приближении вращающейся волны равен

$H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$,

где $\omega$ - резонанс кубита и $\sigma _{x},\sigma _{y}$ являются матрицами Паули .

Чтобы реализовать вращение вокруг $X$ ось, можно установить ${\mathcal {E}}^{y}(t)=0$ и подать микроволновый импульс на частоте $\omega _{d}=\omega$ на время $t_{g}$. Результирующее преобразование

$U_{x}=\exp \left\{-{\frac {i}{\hbar }}\int _{0}^{t_{g}}H^{R}dt\right\}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}$.

Это и есть оператор вращения $R_{X}(\theta )$ по углу $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ о $X$ ось в сфере Блоха. Вращение вокруг $Y$ ось может быть реализована аналогичным образом. Показ двух операторов вращения достаточен для обеспечения универсальности , поскольку каждый унитарный оператор отдельного кубита $U$ может быть представлен как $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ (вплоть до глобальной фазы , которая физически несущественна) с помощью процедуры, известной как $X-Y$ разложение. Параметр $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ приводит к трансформации

$U_{x}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}=e^{-i\pi \sigma _{x}/2}=-i\sigma _{x}$

до глобальной фазы $-i$ и известен как ворота НЕ .

Связывание кубитов

Возможность связывать кубиты необходима для реализации двухкубитных вентилей . Соединение двух кубитов может быть достигнуто путем подключения обоих к промежуточной электрической цепи связи. Схема может быть либо фиксированным элементом (например, конденсатором), либо управляемой (например, DC-SQUID ). В первом случае развязка кубитов на время выключения вентиля достигается за счет вывода кубитов из резонанса друг от друга, делая энергетические зазоры между их вычислительными состояниями разными. Этот подход по своей сути ограничен связью ближайших соседей, поскольку между соединенными кубитами должна быть проложена физическая электрическая цепь. Примечательно, что D-Wave Systems соединение ближайших соседей обеспечивает сильно связанную элементарную ячейку из 8 кубитов в конфигурации графа Химеры. Квантовые алгоритмы обычно требуют связи между произвольными кубитами. Следовательно, необходимы несколько операций обмена , что ограничивает возможную длину квантовых вычислений до декогеренции процессора .

Сколько автобус

Другой метод соединения двух или более кубитов — с помощью квантовой шины , путем соединения кубитов с этим промежуточным звеном. Квантовая шина часто реализуется в виде микроволнового резонатора, моделируемого квантовым гармоническим генератором. Связанные кубиты могут входить в резонанс с шиной и друг с другом и выходить из него, устраняя ограничение на количество ближайших соседей. Формализм, описывающий взаимодействие, представляет собой квантовую электродинамику полости . В квантовой электродинамике резонаторов кубиты аналогичны атомам, взаимодействующим с оптическим фотонным резонатором с разницей в ГГц (а не в ТГц режиме электромагнитного излучения). Резонансный обмен возбуждениями между этими искусственными атомами потенциально полезен для прямой реализации многокубитных вентилей. темного состояния Следуя многообразию , схема Хазали-Мёлмера выполняет сложные многокубитные операции за один шаг, существенно упрощая традиционную модель схемы.

Перекрестный резонансный затвор

Один популярный механизм вентилирования использует два кубита и шину, каждый из которых настроен на разное разделение энергетических уровней. Применение микроволнового возбуждения к первому кубиту с частотой, резонансной со вторым кубитом, вызывает $\sigma _{x}$ вращение второго кубита. Направление вращения зависит от состояния первого кубита, что позволяет создать управляемую конструкцию фазового вентиля .

Следуя обозначениям гамильтониан движения, описывающий возбужденную систему через первую линию движения кубита, формально записывается

$H_{D}/\hbar =A(t)\cos({\tilde {\omega }}_{2}t)\left(\sigma _{x}\otimes I-{\frac {J}{\Delta _{12}}}\sigma _{z}\otimes \sigma _{x}+m_{12}I\otimes \sigma _{x}\right)$,

где $A(t)$ – форма микроволнового импульса во времени, ${\tilde {\omega }}_{2}$ — резонансная частота второго кубита, $\{I,\sigma _{x},\sigma _{y},\sigma _{z}\}$ – матрицы Паули , $J$ - коэффициент связи между двумя кубитами через резонатор, $\Delta _{12}\equiv \omega _{1}-\omega _{2}$ это расстройка кубита, $m_{12}$ это случайная (нежелательная) связь между кубитами, и $\hbar$ постоянная Планка, разделенная на $2\pi$. времени Интеграл по $A(t)$ определяет угол поворота. Нежелательные вращения первого и третьего членов гамильтониана можно компенсировать с помощью операций с одним кубитом. Оставшийся компонент в сочетании с вращениями одного кубита образует основу su(4) алгебры Ли .

Геометрические фазовые ворота

Более высокие уровни (за пределами вычислительного подпространства) пары связанных сверхпроводящих цепей можно использовать для индуцирования геометрической фазы в одном из вычислительных состояний кубитов. Это приводит к запутанному условному фазовому сдвигу соответствующих состояний кубита. Этот эффект был реализован путем настройки потока спектров кубитов. и с использованием избирательного микроволнового управления. Внерезонансное возбуждение можно использовать для индукции дифференциального сдвига переменного тока, что позволяет реализовать полностью микроволновые вентили с управляемой фазой.

Гейзенберговские взаимодействия

Модель взаимодействий Гейзенберга, записанная как

${\hat {\mathcal {H}}}_{\mathrm {XXZ} }/\hbar =\sum _{i,j}J_{\mathrm {XY} }({\hat {\sigma }}_{\text{x}}^{i}{\hat {\sigma }}_{\text{x}}^{j}+{\hat {\sigma }}_{\text{y}}^{i}{\hat {\sigma }}_{\text{y}}^{j})+J_{\mathrm {ZZ} }{\hat {\sigma }}_{\text{z}}^{i}{\hat {\sigma }}_{\text{z}}^{j}$,

служит основой для аналогового квантового моделирования спиновых систем и примитивом для выразительного набора квантовых вентилей, иногда называемых вентилями фермионного моделирования (или fSim ). В сверхпроводящих схемах эта модель взаимодействия была реализована с использованием настраиваемых по потоку кубитов с настраиваемой по потоку связью. позволяя продемонстрировать квантовое превосходство. Кроме того, это также может быть реализовано в кубитах с фиксированной частотой и фиксированной связью с использованием СВЧ-приводов. Семейство вентилей fSim включает произвольные двухкубитные унитарные элементы XY и ZZ, включая вентили iSWAP, CZ и SWAP (см. Квантовые логические вентили ).

Показания кубита

, зависящие от архитектуры Существуют механизмы считывания или измерения . Считывание фазового кубита объясняется в таблице архетипов кубита выше. Состояние потока кубита часто считывается с помощью регулируемого DC- SQUID магнитометра . Состояния также можно измерять с помощью электрометра . Более общая схема считывания включает связь с микроволновым резонатором , где резонансная частота резонатора дисперсионно смещается состоянием кубита. Многоуровневые системы (кудиты) можно считывать с помощью электронных стеллажей.

Критерии ДиВинченцо

Критерии ДиВинченцо представляют собой список, описывающий требования к физической системе, способной реализовать логический кубит. Критериям ДиВинченцо удовлетворяет реализация сверхпроводящих квантовых вычислений. Большая часть текущих усилий по разработке сверхпроводящих квантовых вычислений направлена ​​на достижение межсоединения, управления и считывания в 3-м измерении с дополнительными слоями литографии. Список критериев Ди Винченцо для физической системы, реализующей логический кубит, удовлетворяется реализацией сверхпроводящих кубитов. . Хотя первоначально предложенные критерии ДиВинченцо состоят из пяти критериев, необходимых для физической реализации квантового компьютера, более полный список состоит из семи критериев, поскольку он учитывает связь по компьютерной сети, способной передавать квантовую информацию между компьютерами, известную как «квантовый Интернет». ». Таким образом, первые пять критериев обеспечивают успешные квантовые вычисления, а последние два критерия обеспечивают квантовую связь.

1. Масштабируемая физическая система с хорошо охарактеризованными кубитами. «Хорошо охарактеризованная подразумевает, что эта функция Гамильтона должна быть четко определена, т.е. собственные состояния энергии кубита должны иметь возможность количественного определения. Больше кубитов В этом заключается основная проблема, с которой сталкиваются квантовые компьютеры, поскольку внедрение большего количества кубитов приводит к экспоненциальному увеличению стоимости и других физических реализаций, которые меркнут по сравнению с повышенной скоростью, которую они могут предложить. Поскольку сверхпроводящие кубиты изготавливаются на чипе, многокубитную систему легко масштабировать. Кубиты расположены на 2D-поверхности чипа. Потребность в хорошо охарактеризованных кубитах удовлетворяется за счет (а) нелинейности кубита (доступ только к двум доступным уровням энергии) и (б) доступа к одному кубиту за раз (а не ко всей многокубитной системе) посредством выделенные линии управления для каждого кубита и/или частотное разделение или отстройка разных кубитов.
2. Возможность инициализировать состояние кубитов до простого контрольного состояния. Фидуциальное состояние — это состояние, которое легко и последовательно воспроизвести и которое полезно в квантовых вычислениях, поскольку его можно использовать для гарантии исходного состояния кубитов. Один из простых способов инициализировать сверхпроводящий кубит — подождать достаточно долго, пока кубиты релаксируют до основного состояния. Управление потенциалом кубита с помощью ручек настройки позволяет ускорить механизмы инициализации.
3. Длительное время декогеренции . На декогерентность сверхпроводящих кубитов влияет множество факторов. Большая часть декогеренции связана с качеством джозефсоновского перехода и дефектами подложки чипа. Из-за своего мезоскопического масштаба сверхпроводящие кубиты относительно недолговечны. Тем не менее, в этих многокубитных системах были продемонстрированы тысячи операций вентиля. Недавние стратегии по улучшению когерентности устройств включают очистку материалов схемы и разработку кубитов с пониженной чувствительностью к источникам шума.
4. «Универсальный» набор квантовых вентилей. Сверхпроводящие кубиты допускают произвольные вращения в сфере Блоха с помощью импульсных микроволновых сигналов, реализуя одиночные кубитовые вентили. $\sigma _{z}\sigma _{z}$ и $\sigma _{x}\sigma _{x}$ муфты показаны для большинства реализаций и для дополнения универсального набора вентилей. Этот критерий также может быть удовлетворен путем соединения двух трансмонов с помощью разделительного конденсатора.
5. Возможность измерения кубитов. Обычно одиночные сверхпроводящие кубиты используются для управления или измерения.
6. Взаимоконвертируемость стационарных и летающих кубитов. В то время как стационарные кубиты используются для хранения информации или выполнения вычислений, летающие кубиты передают информацию макроскопически. Кубиты должны иметь возможность превращаться из стационарного кубита в летающий кубит и наоборот.
7. Надежная передача летающих кубитов между указанными местами.

Последние два критерия были экспериментально подтверждены исследованиями, проведенными ETH с двумя сверхпроводящими кубитами, соединенными коаксиальным кабелем .

Проблемы

Одной из основных проблем сверхпроводящих квантовых вычислений являются чрезвычайно низкие температуры, при которых существуют сверхпроводники, такие как конденсаты Бозе-Эйнштейна. Другими основными проблемами при проектировании сверхпроводящих кубитов являются формирование потенциальной ямы и выбор массы частиц таким образом, чтобы энергетическое разделение между двумя конкретными энергетическими уровнями было уникальным, отличающимся от всех других межуровневых энергетических разделений в системе, поскольку эти два уровня используются как логические состояния кубит.

Сверхпроводящие квантовые вычисления должны также смягчать квантовый шум (нарушения работы системы, вызванные ее взаимодействием с окружающей средой), а также утечку (потеря информации в окружающую среду). Одним из способов уменьшения утечки является измерение четности . Другая стратегия — использовать кубиты с большой ангармоничностью. Многие текущие проблемы, с которыми сталкиваются сверхпроводящие квантовые вычисления, лежат в области микроволновой техники. По мере того, как сверхпроводящие квантовые вычисления приближаются к более масштабным устройствам, исследователи сталкиваются с трудностями в обеспечении когерентности кубитов , масштабируемом программном обеспечении для калибровки , эффективном определении точности квантовых состояний по всему чипу, а также точности кубитов и вентилей. Более того, сверхпроводящие квантовые вычислительные устройства должны быть надежно воспроизводимы во все более крупных масштабах, чтобы они были совместимы с этими усовершенствованиями.

Путешествие сверхпроводящих квантовых вычислений:

Хотя это и не новейшая разработка, фокус начал смещаться на сверхпроводящие кубиты во второй половине 1990-х годов, когда стало очевидным квантовое туннелирование через джозефсоновские переходы, что позволило осознать, что с помощью этих сверхпроводящих кубитов можно реализовать квантовые вычисления.

В конце века, в 1999 году, была опубликована статья была опубликована Ясунобу Накамурой, в которой была представлена ​​первоначальная конструкция сверхпроводящего кубита, который теперь известен как «зарядовый кубит». Это основной базовый момент, на основе которого в более поздние проекты вносились поправки. Эти первоначальные кубиты имели свои ограничения в отношении поддержания длительного времени когерентности и разрушительных измерений. Дальнейшие поправки к этому первоначальному прорыву привели к изобретению фазового и потокового кубита, что впоследствии привело к созданию трансмон-кубита, который в настоящее время широко и в основном используется в сверхпроводящих квантовых вычислениях. Трансмон-кубит усовершенствовал первоначальную конструкцию и дополнительно смягчил зарядовый шум от кубит.

Этот путь был долгим, трудным и полным прорывов, но в новейшей истории мы увидели значительные достижения и обладают огромным потенциалом для революции в области вычислений.

Будущее сверхпроводящих квантовых вычислений:

Ведущие гиганты отрасли, такие как Google, IBM и Baidu, используют сверхпроводящие квантовые вычисления и трансмонные кубиты, чтобы добиться прогресса в области квантовых вычислений.

В августе 2022 года Baidu объявила о своих планах по созданию полностью интегрированного квантового компьютера, включающего сверхпроводящие кубиты. В этом компьютере будет полностью интегрировано аппаратное обеспечение, программное обеспечение и приложения. Это первый случай в мире квантовых вычислений, который приведет к революционным достижениям.

IBM публично опубликовала следующую дорожную карту, которую они установили для своих квантовых компьютеров, которая также включает сверхпроводящие кубиты и трансмон-кубиты.

2021: В 2021 году IBM выпустила свой 127-кубитный процессор.

2022: 9 ноября IBM анонсировала свой 433-кубитный процессор под названием Osprey.

2023: IBM планирует выпустить квантовый процессор Condor с 1121 кубитом.

2024: IBM планирует выпустить квантовый процессор Flamingo с более чем 1386 кубитами.

2025: IBM планирует выпустить квантовый процессор Kookaburra с более чем 4158 кубитами.

2026 год и далее: IBM планирует выпустить квантовый процессор, который можно масштабировать с 10 000 кубитов до 100 000 кубитов.

Google в 2016 году реализовал 16 кубитов для демонстрации модели Ферми-Хаббарда . В другом недавнем эксперименте Google использовал 17 кубитов для оптимизации модели Шеррингтона-Киркпатрика . Google создал квантовый компьютер Sycamore, который за 200 секунд выполнил задачу, на которую на классическом компьютере ушло бы 10 000 лет.

Дальнейшее чтение

• Стэнсил, Дэниел Д.; Берд, Грегори Т. (2022). Принципы сверхпроводящих квантовых компьютеров (1-е изд.). Хобокен, Нью-Джерси: John Wiley & Sons. ISBN  978-1-119-75072-7 . OCLC   1302334194 . 978-1-119-75074-1 (электронная книга).

Внешние ссылки

• IBM Quantum предлагает доступ к более чем 20 квантовым компьютерным системам.
• IBM Quantum Experience предлагает бесплатный доступ к написанию квантовых алгоритмов и их выполнению на 5-кубитных квантовых компьютерах.
• Дорожная карта IBM по квантовым вычислениям показывает, что 65 кубитных систем будут доступны в 2020 году, а 127 кубитов будут доступны где-то в 2021 году.