Квантовые вычисления

Quantum System One , квантовый компьютер IBM 2019 года с 20 сверхпроводящими кубитами.

Квантовый компьютер — это компьютер , который использует квантовомеханические явления. В малых масштабах физическая материя проявляет свойства как частиц, так и волн , и квантовые вычисления используют это поведение с помощью специализированного оборудования. Классическая физика не может объяснить работу этих квантовых устройств, а масштабируемый квантовый компьютер может выполнять некоторые вычисления экспоненциально быстрее, чем любой современный «классический» компьютер. В частности, крупномасштабный квантовый компьютер мог бы взламывать широко используемые схемы шифрования и помогать физикам выполнять физическое моделирование ; однако нынешний уровень техники в значительной степени экспериментальный и непрактичный, что затрудняет его полезное применение.

Основная единица информации в квантовых вычислениях, кубит (или «квантовый бит»), выполняет ту же функцию, что и бит в классических вычислениях. Однако, в отличие от классического бита, который может находиться в одном из двух состояний (двоичного ) , кубит может существовать в суперпозиции двух своих «базисных» состояний, что в общих чертах означает, что он находится в обоих состояниях одновременно. При измерении кубита результатом является вероятностный вывод классического бита. Если квантовый компьютер манипулирует кубитом определенным образом, эффекты волновой интерференции могут усилить желаемые результаты измерений. Разработка квантовых алгоритмов предполагает создание процедур, которые позволяют квантовому компьютеру выполнять вычисления эффективно и быстро.

Физическая разработка высококачественных кубитов оказалась сложной задачей. Если физический кубит недостаточно изолирован от своего окружения, он страдает от квантовой декогеренции , вносящей шум в вычисления. Национальные правительства вложили значительные средства в экспериментальные исследования, направленные на разработку масштабируемых кубитов с более длительным временем когерентности и меньшим уровнем ошибок. Двумя наиболее многообещающими технологиями являются сверхпроводники (которые изолируют электрический ток за счет устранения электрического сопротивления ) и ионные ловушки (которые удерживают одну атомную частицу с помощью электромагнитных полей ).

В принципе, классический компьютер может решить те же вычислительные задачи, что и квантовый компьютер, если дать ему достаточно времени. Квантовое преимущество проявляется в форме временной сложности, а не в вычислимости , а теория квантовой сложности показывает, что некоторые квантовые алгоритмы экспоненциально более эффективны, чем самые известные классические алгоритмы. Крупномасштабный квантовый компьютер теоретически мог бы решить вычислительные задачи, неразрешимые классическим компьютером, за любой разумный промежуток времени. Хотя заявления о таком квантовом превосходстве привлекли к этой дисциплине значительное внимание, варианты ее практического использования в краткосрочной перспективе остаются ограниченными.

История

Хронологическое руководство см. в разделе «Хронология квантовых вычислений и связи» .

Интерферометр Маха -Цендера показывает, что фотоны могут проявлять волновую интерференцию .

На протяжении многих лет области квантовой механики и информатики формировали отдельные академические сообщества. Современная квантовая теория была разработана в 1920-х годах для объяснения корпускулярно-волнового дуализма, наблюдаемого на атомных масштабах. а цифровые компьютеры в последующие десятилетия появились , которые заменили человеческие компьютеры для утомительных вычислений. Обе дисциплины имели практическое применение во время Второй мировой войны ; компьютеры сыграли важную роль в криптографии военного времени , а квантовая физика сыграла важную роль в ядерной физике, использованной в Манхэттенском проекте .

Когда физики применили квантово-механические модели к вычислительным задачам и заменили цифровые биты на кубиты , области квантовой механики и информатики начали сближаться.В 1980 году Пол Бениофф представил квантовую машину Тьюринга , которая использует квантовую теорию для описания упрощенного компьютера. Когда цифровые компьютеры стали быстрее, физики столкнулись с экспоненциальным увеличением накладных расходов при моделировании квантовой динамики . что побудило Юрия Манина и Ричарда Фейнмана независимо предположить, что аппаратное обеспечение, основанное на квантовых явлениях, может быть более эффективным для компьютерного моделирования. В статье 1984 года Чарльз Беннетт и Жиль Брассар применили квантовую теорию к протоколам криптографии и продемонстрировали, что квантовое распределение ключей может повысить информационную безопасность .

квантовые алгоритмы появились Затем для решения задач оракула , такие как алгоритм Дойча в 1985 году. алгоритм Бернштейна – Вазирани в 1993 г., и алгоритм Саймона в 1994 году. Эти алгоритмы не решали практических задач, но математически продемонстрировали, что можно получить больше информации, запрашивая черный ящик с квантовым состоянием в суперпозиции , что иногда называют квантовым параллелизмом .

Питер Шор (на фото в 2017 году) показал в 1994 году, что масштабируемый квантовый компьютер сможет взламывать шифрование RSA .

Питер Шор опирался на эти результаты в своих алгоритмах 1994 года для взлома широко используемых протоколов шифрования RSA и Диффи-Хеллмана . который привлек значительное внимание к области квантовых вычислений. В 1996 году алгоритм Гровера установил квантовое ускорение широко применимой задачи неструктурированного поиска. В том же году Сет Ллойд доказал, что квантовые компьютеры могут моделировать квантовые системы без экспоненциальных затрат, присутствующих в классическом моделировании. подтверждение гипотезы Фейнмана 1982 года.

За прошедшие годы экспериментаторы создали небольшие квантовые компьютеры, используя захваченные ионы и сверхпроводники . В 1998 году двухкубитный квантовый компьютер продемонстрировал осуществимость технологии. и последующие эксперименты увеличили количество кубитов и снизили частоту ошибок.

В 2019 году Google AI и NASA объявили, что они достигли квантового превосходства с помощью 54-кубитной машины, выполняющей вычисления, невозможные для любого классического компьютера. Однако обоснованность этого утверждения все еще активно исследуется.

показывает Пороговая теорема , как увеличение количества кубитов может уменьшить ошибки. однако полностью отказоустойчивые квантовые вычисления остаются «довольно далекой мечтой». По мнению некоторых исследователей, шумные квантовые машины промежуточного масштаба ( NISQ ) могут найти специализированное применение в ближайшем будущем, но шум в квантовых вентилях ограничивает их надежность.

Инвестиции в исследования в области квантовых вычислений увеличились в государственном и частном секторах. Как резюмировала одна консалтинговая фирма,

...   инвестиционные доллары текут потоком, а стартапы в области квантовых вычислений множатся.   ... Хотя квантовые вычисления обещают помочь предприятиям решать проблемы, которые находятся за пределами досягаемости и скорости обычных высокопроизводительных компьютеров , на этой ранней стадии варианты использования в основном носят экспериментальный и гипотетический характер.

С точки зрения управления бизнесом, потенциальные применения квантовых вычислений можно разделить на четыре основные категории: кибербезопасность, анализ данных и искусственный интеллект, оптимизация и моделирование, а также управление данными и поиск.

В декабре 2023 года физики впервые сообщили о запутанности отдельных молекул, которая может иметь важные применения в квантовых вычислениях. Также в декабре 2023 года ученые Гарвардского университета успешно создали «квантовые схемы», которые исправляют ошибки более эффективно, чем альтернативные методы, что потенциально может устранить серьезное препятствие для практических квантовых компьютеров. Исследовательскую группу из Гарварда поддерживали Массачусетский технологический институт , QuEra Computing , Калифорнийский технологический институт и Принстонский университет, а также финансировала программа DARPA по оптимизации с помощью квантовых устройств среднего масштаба с шумом (ONISQ). Продолжаются исследовательские усилия по запуску квантовых вычислений с помощью топологических и фотонных подходов.

обработка

См. Также: Введение в квантовую механику.

Компьютерные инженеры обычно описывают работу современного компьютера с точки зрения классической электродинамики .В этих «классических» компьютерах некоторые компоненты (такие как полупроводники и генераторы случайных чисел ) могут полагаться на квантовое поведение, но эти компоненты не изолированы от окружающей среды, поэтому любая квантовая информация быстро декогерируется .Хотя программисты могут полагаться на теорию вероятностей при разработке рандомизированных алгоритмов , квантово-механические понятия, такие как суперпозиция и интерференция, в значительной степени не имеют значения для анализа программ .

Квантовые программы , напротив, полагаются на точный контроль когерентных квантовых систем. Физики описывают эти системы математически, используя линейную алгебру . Комплексные числа моделируют амплитуды вероятности , векторы моделируют квантовые состояния , а матрицы моделируют операции, которые можно выполнять над этими состояниями. Программирование квантового компьютера — это вопрос составления операций таким образом, чтобы полученная программа выдавала полезный результат в теории и была реализуема на практике.

Как физик Чарли Беннетт описывает взаимосвязь между квантовыми и классическими компьютерами:

Классический компьютер — это квантовый компьютер... поэтому нам не следует задаваться вопросом: «Откуда берется квантовое ускорение?» Мы должны сказать: «Ну, все компьютеры квантовые… Откуда берутся классические замедления?»

Квантовая информация

Представление кубита в сфере Блоха . Государство $|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$ — точка на поверхности сферы, находящаяся на полпути между полюсами, $|0\rangle$ и $|1\rangle$.

Подобно тому, как бит является основной концепцией классической теории информации, кубит является фундаментальной единицей квантовой информации . Тот же термин «кубит» используется для обозначения абстрактной математической модели и любой физической системы, представленной этой моделью. Классический бит по определению существует в любом из двух физических состояний, которые можно обозначить 0 и 1. Кубит также описывается состоянием, и два состояния часто обозначаются $|0\rangle$ и $|1\rangle$ служат квантовыми аналогами классических состояний 0 и 1. Однако квантовые состояния $|0\rangle$ и $|1\rangle$ принадлежат векторному пространству , а это означает, что их можно умножать на константы и складывать вместе, и результатом снова будет действительное квантовое состояние. комбинация называется суперпозицией Такая $|0\rangle$ и $|1\rangle$.

Двумерный вектор математически представляет состояние кубита. Физики обычно используют обозначение Дирака для квантовомеханической линейной алгебры , записывая $|\psi \rangle$ ' ket psi ' для вектора с меткой $\psi$ . Поскольку кубит представляет собой систему с двумя состояниями, любое состояние кубита принимает форму $\alpha |0\rangle +\beta |1\rangle$ , где $|0\rangle$ и $|1\rangle$ являются стандартными базисными состояниями , и $\alpha$ и $\beta$ являются амплитудами вероятности , которые в общем являются комплексными числами . Если либо $\alpha$ или $\beta$ равен нулю, кубит фактически является классическим битом; когда оба не равны нулю, кубит находится в суперпозиции. Такой вектор квантового состояния действует аналогично (классическому) вектору вероятности , с одним ключевым отличием: в отличие от вероятностей, амплитуды вероятности не обязательно являются положительными числами. Отрицательные амплитуды допускают деструктивную интерференцию волн.

Когда кубит измеряется в стандартном базисе , результатом является классический бит.Правило Борна описывает соответствие между амплитудами и вероятностями в квадрате нормы - при измерении кубита $\alpha |0\rangle +\beta |1\rangle$ государство разваливается , $|0\rangle$ с вероятностью $|\alpha |^{2}$, или чтобы $|1\rangle$ с вероятностью $|\beta |^{2}$.Любое допустимое состояние кубита имеет коэффициенты $\alpha$ и $\beta$ такой, что $|\alpha |^{2}+|\beta |^{2}=1$.Например, измерение кубита $1/{\sqrt {2}}|0\rangle +1/{\sqrt {2}}|1\rangle$ произведет либо $|0\rangle$ или $|1\rangle$ с равной вероятностью.

Каждый дополнительный кубит удваивает размерность состояний пространства . Например, вектор 1 / √2 |00⟩ + 1 / √2 |01⟩ представляет двухкубитное состояние, тензорное произведение кубита |0⟩ на кубит 1 / √2 |0⟩ + 1 / √2 |1⟩ .Этот вектор обитает в четырехмерном векторном пространстве, натянутом на базисные векторы |00⟩ , |01⟩ , |10⟩ и |11⟩ . Белла Штат 1 / √2 |00⟩ + 1 / √2 |11⟩ невозможно разложить на тензорное произведение двух отдельных кубитов — два кубита запутаны, поскольку их амплитуды вероятности коррелируют .В общем, векторное пространство для системы n -кубитов равно 2 ^н -мерен, и это затрудняет классическому компьютеру симуляцию квантового: для представления 100-кубитной системы требуется хранить 2 ¹⁰⁰ классические ценности.

Унитарные операторы

Смотрите также: Унитарность (физика)

Состоянием этой однокубитной квантовой памяти можно манипулировать, применяя квантовые логические элементы , аналогично тому, как классической памятью можно манипулировать с помощью классических логических элементов . Одним из важных вентилей как для классических, так и для квантовых вычислений является вентиль НЕ, который может быть представлен матрицей

$$X:={\begin{pmatrix}0&1\\1&0\end{pmatrix}}.$$

Математически применение такого логического элемента к вектору квантового состояния моделируется с помощью матричного умножения . Таким образом

$X|0\rangle =|1\rangle$ и $X|1\rangle =|0\rangle$.

Математику однокубитных вентилей можно расширить для работы с многокубитной квантовой памятью двумя важными способами. Один из способов — просто выбрать кубит и применить этот вентиль к целевому кубиту, оставив остальную часть памяти незатронутой. Другой способ — применить гейт к цели, только если другая часть памяти находится в желаемом состоянии. Эти два варианта можно проиллюстрировать на другом примере. Возможные состояния двухкубитной квантовой памяти:

$$|00\rangle :={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\quad |01\rangle :={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}};\quad |10\rangle :={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\quad |11\rangle :={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}.$$

Тогда управляемый вентиль НЕ (CNOT) можно представить с помощью следующей матрицы:

$$\operatorname {CNOT} :={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}}.$$

Как математическое следствие этого определения, ${\textstyle \operatorname {CNOT} |00\rangle =|00\rangle }$, ${\textstyle \operatorname {CNOT} |01\rangle =|01\rangle }$, ${\textstyle \operatorname {CNOT} |10\rangle =|11\rangle }$, и ${\textstyle \operatorname {CNOT} |11\rangle =|10\rangle }$. Другими словами, CNOT применяет вентиль НЕ ( ${\textstyle X}$ от предыдущего) ко второму кубиту тогда и только тогда, когда первый кубит находится в состоянии ${\textstyle |1\rangle }$. Если первый кубит ${\textstyle |0\rangle }$, ни с одним кубитом ничего не делается.

Подводя итог, квантовые вычисления можно описать как сеть квантовых логических элементов и измерений. Однако любое измерение можно отложить до конца квантовых вычислений, хотя эта отсрочка может потребовать вычислительных затрат, поэтому большинство квантовых схем изображают сеть, состоящую только из квантовых логических элементов и без каких-либо измерений.

Квантовый параллелизм

Квантовый параллелизм — это эвристика, согласно которой квантовые компьютеры можно рассматривать как оценку функции для нескольких входных значений одновременно. Этого можно достичь, подготовив квантовую систему в суперпозиции входных состояний и применив унитарное преобразование, которое кодирует функцию, подлежащую оценке. Результирующее состояние кодирует выходные значения функции для всех входных значений в суперпозиции, что позволяет одновременно вычислять несколько выходных значений. Это свойство является ключом к ускорению многих квантовых алгоритмов. Однако «параллелизма» в этом смысле недостаточно для ускорения вычислений, поскольку измерение в конце вычислений дает только одно значение. Чтобы быть полезным, квантовый алгоритм должен также включать в себя какой-то другой концептуальный компонент.

Квантовое программирование

Дополнительная информация: Квантовое программирование.

Существует ряд моделей вычислений для квантовых вычислений, отличающихся основными элементами, на которые разлагаются вычисления.

Массив ворот

Квантовая схема, реализующая вентиль Тоффоли из более примитивных вентилей.

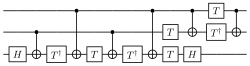
Массив квантовых вентилей разлагает вычисления на последовательность квантовых вентилей размером в несколько кубитов . Квантовые вычисления можно описать как сеть квантовых логических элементов и измерений. Однако любое измерение можно отложить до конца квантовых вычислений, хотя эта отсрочка может потребовать вычислительных затрат, поэтому большинство квантовых схем изображают сеть, состоящую только из квантовых логических элементов и без каких-либо измерений.

Любое квантовое вычисление (которое в приведенном выше формализме представляет собой любую унитарную матрицу размера $2^{n}\times 2^{n}$ над $n$ кубиты) можно представить как сеть квантовых логических элементов из довольно небольшого семейства элементов. Выбор семейства вентилей, обеспечивающий такую ​​конструкцию, известен как универсальный набор вентилей , поскольку компьютер, который может запускать такие схемы, является универсальным квантовым компьютером . Один общий такой набор включает в себя все однокубитные вентили, а также вентиль CNOT сверху. Это означает, что любые квантовые вычисления могут быть выполнены путем выполнения последовательности однокубитных вентилей вместе с вентилями CNOT. Хотя этот набор вентилей бесконечен, его можно заменить конечным набором вентилей, обратившись к теореме Соловея-Китаева .

Квантовые вычисления

Квантовый компьютер, основанный на измерениях, разлагает вычисления на последовательность измерений состояния Белла и однокубитных квантовых вентилей, применяемых к сильно запутанному начальному состоянию ( состоянию кластера ), используя метод, называемый телепортацией квантовых вентилей .

Адиабатические квантовые вычисления

Адиабатический квантовый компьютер , основанный на квантовом отжиге , разлагает вычисления на медленное непрерывное преобразование начального гамильтониана в окончательный гамильтониан, основные состояния которого содержат решение.

Нейроморфные квантовые вычисления

Нейроморфные квантовые вычисления (сокращенно «н.квантовые вычисления») — это нетрадиционный тип вычислений, который использует нейроморфные вычисления для выполнения квантовых операций. Было высказано предположение, что квантовые алгоритмы , являющиеся алгоритмами, работающими на реалистичной модели квантовых вычислений , могут вычисляться одинаково эффективно с нейроморфными квантовыми вычислениями. И традиционные квантовые вычисления , и нейроморфные квантовые вычисления представляют собой основанные на физике нетрадиционные вычислительные подходы к вычислениям и не следуют архитектуре фон Неймана . Они оба создают систему (схему), которая представляет рассматриваемую физическую проблему, а затем используют соответствующие физические свойства системы для поиска «минимума». Нейроморфные квантовые вычисления и квантовые вычисления имеют схожие физические свойства во время вычислений.

квантовые

Топологический квантовый компьютер разлагает вычисления на сплетение анионов в двумерную решетку.

Квантовая машина Тьюринга

Квантовая машина Тьюринга — это квантовый аналог машины Тьюринга . Все эти модели вычислений — квантовые схемы, односторонние квантовые вычисления, адиабатические квантовые вычисления, и топологические квантовые вычисления — было показано, что они эквивалентны квантовой машине Тьюринга; при идеальной реализации одного такого квантового компьютера он может моделировать все остальные с не более чем полиномиальными издержками. Эта эквивалентность не обязательно справедлива для практических квантовых компьютеров, поскольку накладные расходы на моделирование могут быть слишком большими, чтобы быть практичными.

и

Квантовые вычисления имеют значительные потенциальные применения в области криптографии и кибербезопасности. Квантовая криптография, основанная на принципах квантовой механики, предлагает возможность создания безопасных каналов связи, устойчивых к подслушиванию. Протоколы квантового распределения ключей (QKD), такие как BB84, обеспечивают безопасный обмен криптографическими ключами между сторонами, обеспечивая конфиденциальность и целостность связи. Более того, квантовые генераторы случайных чисел (QRNG) могут генерировать высококачественные случайные числа, которые необходимы для безопасного шифрования.

Однако квантовые вычисления также создают проблемы для традиционных криптографических систем. Алгоритм Шора, квантовый алгоритм факторизации целых чисел, потенциально может разрушить широко используемые схемы криптографии с открытым ключом, такие как RSA, которые основаны на сложности факторизации больших чисел. Постквантовая криптография, предполагающая разработку криптографических алгоритмов, устойчивых к атакам как классических, так и квантовых компьютеров, является активной областью исследований, направленных на решение этой проблемы.

Продолжающиеся исследования в области квантовой криптографии и постквантовой криптографии имеют решающее значение для обеспечения безопасности связи и данных в условиях развития возможностей квантовых вычислений. Достижения в этих областях, такие как разработка новых протоколов QKD, усовершенствование QRNG и стандартизация постквантовых криптографических алгоритмов, будут играть ключевую роль в поддержании целостности и конфиденциальности информации в квантовую эпоху.

Общение

Дополнительная информация: Квантовая информатика.

Квантовая криптография открывает новые способы безопасной передачи данных; например, квантовое распределение ключей использует запутанные квантовые состояния для создания безопасных криптографических ключей . Когда отправитель и получатель обмениваются квантовыми состояниями, они могут гарантировать, что противник не перехватит сообщение, поскольку любой несанкционированный перехватчик нарушит хрупкую квантовую систему и внесет заметные изменения. Таким образом, с помощью соответствующих криптографических протоколов отправитель и получатель могут установить общую конфиденциальную информацию, устойчивую к подслушиванию.

Современные оптоволоконные кабели способны передавать квантовую информацию на относительно короткие расстояния. Продолжающиеся экспериментальные исследования направлены на разработку более надежного оборудования (например, квантовых повторителей) в надежде масштабировать эту технологию для квантовых сетей на большие расстояния со сквозной запутанностью. Теоретически это может позволить реализовать новые технологические приложения, такие как распределенные квантовые вычисления и расширенное квантовое зондирование .

Алгоритмы

Прогресс в поиске квантовых алгоритмов обычно сосредоточен на этой модели квантовой схемы, хотя существуют исключения, такие как квантовый адиабатический алгоритм . Квантовые алгоритмы можно грубо классифицировать по типу ускорения, достигнутого по сравнению с соответствующими классическими алгоритмами.

Квантовые алгоритмы, которые предлагают больше, чем полиномиальное ускорение по сравнению с самым известным классическим алгоритмом, включают алгоритм Шора для факторизации и связанные с ним квантовые алгоритмы для вычисления дискретных логарифмов , решения уравнения Пелля и, в более общем плане, решения проблемы скрытых подгрупп для абелевых конечных групп. Эти алгоритмы зависят от примитива квантового преобразования Фурье . Не было найдено математического доказательства того, что столь же быстрый классический алгоритм не может быть найден, но данные свидетельствуют о том, что это маловероятно. Определенные задачи оракула, такие как проблема Саймона и проблема Бернштейна-Вазирани , действительно дают доказуемое ускорение, хотя это относится к модели квантовых запросов , которая представляет собой ограниченную модель, в которой гораздо легче доказать нижние границы и не обязательно приводит к ускорению для практических задач. .

Другие задачи, включая моделирование квантово-физических процессов из химии и физики твердого тела, аппроксимацию некоторых полиномов Джонса и квантовый алгоритм для линейных систем уравнений, имеют квантовые алгоритмы, которые, по-видимому, дают суперполиномиальное ускорение и являются BQP -полными. Поскольку эти задачи BQP-полны, столь же быстрый классический алгоритм для них будет означать, что ни один квантовый алгоритм не даст суперполиномиального ускорения, что считается маловероятным.

Некоторые квантовые алгоритмы, такие как алгоритм Гровера и усиление амплитуды , дают полиномиальное ускорение по сравнению с соответствующими классическими алгоритмами. Хотя эти алгоритмы дают сравнительно скромное квадратичное ускорение, они широко применимы и, таким образом, дают ускорение для широкого круга задач.

Моделирование квантовых систем

Основная статья: Квантовое моделирование

Поскольку химия и нанотехнологии полагаются на понимание квантовых систем, а такие системы невозможно эффективно смоделировать классическим способом, квантовое моделирование может стать важным применением квантовых вычислений. Квантовое моделирование также можно использовать для моделирования поведения атомов и частиц в необычных условиях, таких как реакции внутри коллайдера . В июне 2023 года ученые-компьютерщики IBM сообщили, что квантовый компьютер дает лучшие результаты при решении физических задач, чем обычный суперкомпьютер.

Около 2% годового мирового производства энергии используется для фиксации азота с целью производства аммиака для процесса Габера в промышленности сельскохозяйственных удобрений (хотя естественные организмы также производят аммиак). Квантовое моделирование может быть использовано для понимания этого процесса и повышения энергоэффективности производства. Ожидается, что на первых порах квантовые вычисления будут использоваться для моделирования, которое повысит эффективность процесса Габера-Боша. к середине 2020-х годов хотя некоторые предсказывали, что это займет больше времени.

Постквантовая криптография

Основная статья: Постквантовая криптография

Заметным применением квантовых вычислений являются атаки на используемые в настоящее время криптографические системы. Факторизация целых чисел , лежащая в основе безопасности криптографических систем с открытым ключом, считается невозможной с вычислительной точки зрения на обычном компьютере для больших целых чисел, если они являются произведением нескольких простых чисел (например, произведения двух простых чисел по 300 цифр). Для сравнения, квантовый компьютер мог бы решить эту проблему экспоненциально быстрее, используя алгоритм Шора для поиска ее факторов. Эта способность позволила бы квантовому компьютеру взломать многие из используемых сегодня криптографических систем в том смысле, что для решения проблемы будет существовать полиномиальный по времени (по числу цифр целого числа) алгоритм. В частности, большинство популярных шифров с открытым ключом основаны на сложности факторизации целых чисел или задаче дискретного логарифма , обе из которых могут быть решены с помощью алгоритма Шора. В частности, RSA , Диффи-Хеллмана и эллиптической кривой Диффи-Хеллмана могут быть нарушены алгоритмы . Они используются для защиты безопасных веб-страниц, зашифрованной электронной почты и многих других типов данных. Нарушение этих правил будет иметь серьезные последствия для электронной конфиденциальности и безопасности.

Идентификация криптографических систем, которые могут быть защищены от квантовых алгоритмов, является активно исследуемой темой в области постквантовой криптографии . Некоторые алгоритмы с открытым ключом основаны на проблемах, отличных от проблем целочисленной факторизации и задач дискретного логарифма, к которым применяется алгоритм Шора, например, криптосистема МакЭлиса, основанная на проблеме теории кодирования . Также известно, что криптосистемы на основе решеток не могут быть взломаны квантовыми компьютерами, и поиск алгоритма с полиномиальным временем для решения проблемы скрытых диэдральных подгрупп , который сломал бы многие криптосистемы на основе решетки, является хорошо изученной открытой проблемой. Доказано, что применение алгоритма Гровера для взлома симметричного алгоритма (секретного ключа) методом перебора требует времени, равного примерно 2 ^{н /2} вызовов основного криптографического алгоритма по сравнению примерно с 2 ^н в классическом случае это означает, что длина симметричных ключей фактически уменьшается вдвое: AES-256 будет иметь ту же защиту от атаки с использованием алгоритма Гровера, что и AES-128 против классического поиска методом перебора (см. Размер ключа ).

Проблемы с поиском

Основная статья: алгоритм Гровера

Самый известный пример задачи, допускающей полиномиальное квантовое ускорение, — это неструктурированный поиск , который включает в себя поиск отмеченного элемента из списка $n$ элементы в базе данных. Эту проблему можно решить с помощью алгоритма Гровера, используя $O({\sqrt {n}})$ запросов к базе данных, квадратично меньше, чем $\Omega (n)$ запросы, необходимые для классических алгоритмов. В этом случае преимущество не только доказуемо, но и оптимально: было показано, что алгоритм Гровера дает максимально возможную вероятность найти искомый элемент при любом количестве поисков оракула. Многие примеры доказуемого квантового ускорения для задач запросов основаны на алгоритме Гровера, включая алгоритм Брассара, Хойера и Тэппа для поиска коллизий в функциях два к одному. и алгоритм Фари, Голдстоуна и Гутмана для оценки деревьев NAND.

Проблемы, которые можно эффективно решить с помощью алгоритма Гровера, обладают следующими свойствами:

1. В коллекции возможных ответов нет структуры для поиска,
2. Количество возможных ответов для проверки такое же, как количество входных данных алгоритма, и
3. Существует логическая функция, которая оценивает каждый входной сигнал и определяет, является ли он правильным ответом.

Для задач со всеми этими свойствами время работы алгоритма Гровера на квантовом компьютере масштабируется как квадратный корень из количества входных данных (или элементов в базе данных), в отличие от линейного масштабирования классических алгоритмов. Общий класс задач, к которым можно применить алгоритм Гровера. — это булева проблема выполнимости , где база данных , через которую проходит алгоритм, представляет собой базу данных всех возможных ответов. Примером и возможным применением этого является взломщик паролей , который пытается угадать пароль. Взлом симметричных шифров с помощью этого алгоритма представляет интерес для государственных органов.

Квантовый отжиг

Квантовый отжиг основан на адиабатической теореме для проведения расчетов. Система помещается в основное состояние для простого гамильтониана, который медленно развивается к более сложному гамильтониану, основное состояние которого представляет собой решение рассматриваемой проблемы. Адиабатическая теорема утверждает, что если эволюция достаточно медленная, система будет оставаться в своем основном состоянии на протяжении всего процесса. Адиабатическая оптимизация может быть полезна для решения вычислительной биологии . задач

Машинное обучение

Основная статья: Квантовое машинное обучение

Поскольку квантовые компьютеры могут выдавать результаты, которые классические компьютеры не могут эффективно производить, и поскольку квантовые вычисления по своей сути являются линейными алгебраическими, некоторые выражают надежду на разработку квантовых алгоритмов, которые могут ускорить задачи машинного обучения .

Например, считается, что алгоритм HHL , названный в честь его первооткрывателей Харроу, Хасидима и Ллойда, обеспечивает ускорение по сравнению с классическими аналогами. Некоторые исследовательские группы недавно изучили возможность использования оборудования квантового отжига для обучения машин Больцмана и глубоких нейронных сетей .

Модели глубокой генеративной химии становятся мощными инструментами для ускорения открытия лекарств . Однако огромный размер и сложность структурного пространства всех возможных молекул, подобных лекарствам, создают серьезные препятствия, которые в будущем могут быть преодолены с помощью квантовых компьютеров. Квантовые компьютеры, естественно, хороши для решения сложных квантовых задач многих тел. и, таким образом, может сыграть важную роль в приложениях, связанных с квантовой химией. Следовательно, можно ожидать, что генеративные модели с квантовым усилением включая квантовые GAN в конечном итоге могут быть преобразованы в совершенные алгоритмы генеративной химии.

Инженерное дело

Пластина адиабатических компьютеров квантовых

По состоянию на 2023 год классические компьютеры превосходят квантовые компьютеры во всех реальных приложениях. Хотя современные квантовые компьютеры могут ускорить решение конкретных математических задач, они не дают никаких вычислительных преимуществ для практических задач. Ученые и инженеры изучают множество технологий для аппаратного обеспечения квантовых вычислений и надеются разработать масштабируемые квантовые архитектуры, но остаются серьезные препятствия.

Проблемы

При создании крупномасштабного квантового компьютера существует ряд технических проблем. Физик Дэвид ДиВинченцо перечислил эти требования к практическому квантовому компьютеру:

• Физически масштабируемый для увеличения количества кубитов.
• Кубиты, которые можно инициализировать произвольными значениями
• Квантовые вентили, которые быстрее декогеренции времени
• Универсальный комплект ворот
• Кубиты, которые можно легко прочитать.

Поиск запчастей для квантовых компьютеров также очень сложен. Сверхпроводящие квантовые компьютеры , подобные тем, что созданы Google и IBM , нуждаются в гелии-3 , побочном продукте ядерных исследований, и специальных сверхпроводящих кабелях, производимых только японской компанией Coax Co.

Управление многокубитными системами требует генерации и координации большого количества электрических сигналов с жестким и детерминированным временным разрешением. Это привело к разработке квантовых контроллеров , которые позволяют взаимодействовать с кубитами. Масштабирование этих систем для поддержки растущего числа кубитов является дополнительной проблемой.

Декогеренция

Одной из самых больших проблем, связанных с созданием квантовых компьютеров, является контроль или устранение квантовой декогеренции . Обычно это означает изоляцию системы от окружающей среды, поскольку взаимодействие с внешним миром приводит к декогерентности системы. Однако существуют и другие источники декогеренции. Примеры включают квантовые вентили, колебания решетки и фоновый термоядерный спин физической системы, используемый для реализации кубитов. Декогеренция необратима, поскольку она фактически не унитарна, и обычно ее следует строго контролировать, если не избегать. Время декогеренции для систем-кандидатов, в частности, время поперечной релаксации T ₂ (для технологий ЯМР и МРТ , также называемое временем дефазировки ), обычно находится в диапазоне от наносекунд до секунд при низкой температуре. В настоящее время некоторые квантовые компьютеры требуют охлаждения своих кубитов до 20 милликельвинов (обычно с использованием холодильника разбавления). ), чтобы предотвратить значительную декогеренцию. Исследование 2020 года утверждает, что ионизирующее излучение, такое как космические лучи, тем не менее, может привести к декогеренции определенных систем в течение миллисекунд.

В результате трудоемкие задачи могут привести к неработоспособности некоторых квантовых алгоритмов, поскольку попытка поддерживать состояние кубитов в течение достаточно длительного периода времени в конечном итоге приведет к повреждению суперпозиций.

Эти проблемы более сложны для оптических подходов, поскольку временные рамки на порядки короче, а часто упоминаемым подходом к их преодолению является формирование оптического импульса . Частота ошибок обычно пропорциональна отношению времени работы ко времени декогеренции, поэтому любая операция должна быть завершена гораздо быстрее, чем время декогеренции.

Как описано в пороговой теореме , если частота ошибок достаточно мала, считается возможным использовать квантовую коррекцию ошибок для подавления ошибок и декогеренции. Это позволяет общему времени расчета превышать время декогеренции, если схема исправления ошибок может исправлять ошибки быстрее, чем их вносит декогерентность. Часто цитируемая цифра требуемой частоты ошибок в каждом вентиле для отказоустойчивых вычислений равна 10. ⁻³ , предполагая, что шум является деполяризующим.

Выполнение этого условия масштабируемости возможно для широкого спектра систем. Однако использование исправления ошибок приводит к значительному увеличению количества необходимых кубитов. Число, необходимое для факторизации целых чисел с использованием алгоритма Шора, по-прежнему полиномиально и считается между L и L. ² , где L — количество цифр числа, подлежащего факторизации; коэффициент L. алгоритмы исправления ошибок увеличили бы эту цифру на дополнительный Для 1000-битного числа это подразумевает необходимость около 10 ⁴ бит без исправления ошибок. При исправлении ошибок эта цифра увеличится примерно до 10. ⁷ биты. Время расчета около L ² или около 10 ⁷ шагов и на частоте 1   МГц около 10 секунд. Однако накладные расходы на кодирование и исправление ошибок увеличивают размер настоящего отказоустойчивого квантового компьютера на несколько порядков. Тщательные оценки показывают, что по крайней мере 3   миллиона физических кубитов будут учитывать 2048-битное целое число за 5 месяцев на квантовом компьютере с полностью исправленными ошибками. Что касается количества физических кубитов, на сегодняшний день это остается самая низкая оценка. для практически полезной задачи факторизации целых чисел размером 1024 бита или больше.

Другой подход к проблеме стабильности-декогеренции заключается в создании топологического квантового компьютера с анионами , квазичастицами, используемыми в качестве потоков, и использовании теории кос для формирования стабильных логических элементов.

Квантовое превосходство

Физик Джон Прескилл придумал термин «квантовое превосходство» , чтобы описать инженерный подвиг, демонстрирующий, что программируемое квантовое устройство может решить проблему, выходящую за рамки возможностей современных классических компьютеров. Проблема не обязательно должна быть полезной, поэтому некоторые рассматривают тест квантового превосходства только как потенциальный будущий ориентир.

В октябре 2019 года Google AI Quantum при поддержке НАСА стал первым, кто заявил, что достиг квантового превосходства, выполняя вычисления на квантовом компьютере Sycamore более чем в 3 000 000 раз быстрее, чем они могли бы быть выполнены на Summit , который обычно считается самым быстрым в мире. компьютер. Впоследствии это утверждение было оспорено: IBM заявила, что Summit может выполнять образцы намного быстрее, чем заявлено. и с тех пор исследователи разработали более совершенные алгоритмы для решения проблемы выборки, используемые для утверждения квантового превосходства, что существенно сокращает разрыв между Sycamore и классическими суперкомпьютерами. и даже победить его.

В декабре 2020 года группа из USTC реализовала тип выборки бозонов на 76 фотонах с помощью фотонного квантового компьютера Jiuzhang , чтобы продемонстрировать квантовое превосходство. Авторы утверждают, что классическому современному суперкомпьютеру потребуется вычислительное время в 600 миллионов лет, чтобы сгенерировать количество выборок, которое их квантовый процессор может сгенерировать за 20 секунд.

Заявления о квантовом превосходстве вызвали ажиотаж вокруг квантовых вычислений. но они основаны на надуманных тестовых задачах, которые напрямую не подразумевают полезных реальных приложений.

В январе 2024 года исследование, опубликованное в Physical Review Letters , обеспечило прямую проверку экспериментов по квантовому превосходству путем расчета точных амплитуд для экспериментально сгенерированных битовых строк с использованием суперкомпьютера Sunway нового поколения, продемонстрировав значительный скачок в возможностях моделирования, основанных на сжатии тензорной сети с несколькими амплитудами. алгоритм. Это событие подчеркивает развивающуюся среду квантовых вычислений, подчеркивая как прогресс, так и сложности, связанные с проверкой заявлений о квантовом превосходстве.

Скептицизм

Несмотря на большие надежды на квантовые вычисления, значительный прогресс в аппаратном обеспечении и оптимизм в отношении будущих приложений, в статье Nature в 2023 году современные квантовые компьютеры резюмировались как «На данный момент [годны] абсолютно ни для чего». В статье уточняется, что квантовые компьютеры в любом случае еще не стали более полезными и эффективными, чем обычные компьютеры, хотя также утверждается, что в долгосрочной перспективе такие компьютеры, вероятно, будут полезны. 2023 г. «Сообщения ACM» от Статья обнаружил, что текущие алгоритмы квантовых вычислений «недостаточны для практического квантового преимущества без значительных улучшений в программно-аппаратном комплексе». В нем утверждается, что наиболее многообещающими кандидатами на достижение ускорения с помощью квантовых компьютеров являются «проблемы малых данных», например, в химии и материаловедении. Однако в статье также делается вывод, что широкий спектр рассмотренных потенциальных приложений, таких как машинное обучение, «не удастся достичь квантового преимущества с помощью существующих квантовых алгоритмов в обозримом будущем», и определены ограничения ввода-вывода, которые делают ускорение маловероятным. «Проблемы больших данных, неструктурированные линейные системы и поиск в базе данных на основе алгоритма Гровера».

Такое положение дел можно объяснить несколькими текущими и долгосрочными соображениями.

• Традиционное компьютерное оборудование и алгоритмы не только оптимизированы для практических задач, но и продолжают быстро совершенствоваться, особенно графических процессоров . ускорители
• Современное оборудование для квантовых вычислений генерирует лишь ограниченную степень запутанности , прежде чем его захлестнет шум.
• Квантовые алгоритмы обеспечивают ускорение по сравнению с традиционными алгоритмами только для некоторых задач, и сопоставление этих задач с практическими приложениями оказалось сложной задачей. Некоторые многообещающие задачи и приложения требуют ресурсов, значительно превышающих те, которые доступны сегодня. В частности, обработка больших объемов неквантовых данных является проблемой для квантовых компьютеров.
• Некоторые перспективные алгоритмы были «деквантованы», т.е. найдены их неквантовые аналоги аналогичной сложности.
• Если квантовая коррекция ошибок используется для масштабирования квантовых компьютеров для практических приложений, ее накладные расходы могут подорвать ускорение, обеспечиваемое многими квантовыми алгоритмами.
• Анализ сложности алгоритмов иногда делает абстрактные предположения, которые не выполняются в приложениях. Например, входные данные могут быть недоступны, закодированные в квантовых состояниях, а «функции оракула», используемые в алгоритме Гровера, часто имеют внутреннюю структуру, которую можно использовать для более быстрых алгоритмов.

В частности, создание компьютеров с большим количеством кубитов может быть бесполезным, если эти кубиты недостаточно хорошо связаны и не могут поддерживать достаточно высокую степень запутанности в течение длительного времени. Пытаясь превзойти обычные компьютеры, исследователи квантовых вычислений часто ищут новые задачи, которые можно решить на квантовых компьютерах, но это оставляет возможность того, что в ответ будут разработаны эффективные неквантовые методы, как это видно на примере демонстрации квантового превосходства . Поэтому желательно доказать нижние границы сложности наилучших возможных неквантовых алгоритмов (которые могут быть неизвестны) и показать, что некоторые квантовые алгоритмы бессимптомно улучшают эти границы.

Некоторые исследователи выразили скептицизм по поводу возможности создания масштабируемых квантовых компьютеров, обычно из-за проблемы поддержания согласованности в больших масштабах, но также и по другим причинам.

Билл Унру усомнился в практичности квантовых компьютеров в статье, опубликованной в 1994 году. Пол Дэвис утверждал, что компьютер с 400 кубитами даже вступит в конфликт с космологической информацией, связанной с голографическим принципом . Скептики, такие как Гил Калаи, сомневаются, что квантовое превосходство когда-либо будет достигнуто. Физик Михаил Дьяконов выразил скептицизм по поводу квантовых вычислений следующим образом:

«Таким образом, количество непрерывных параметров, описывающих состояние такого полезного квантового компьютера в любой момент времени, должно составлять… около 10 ³⁰⁰ ... Сможем ли мы когда-нибудь научиться контролировать более 10 ³⁰⁰ непрерывно изменяющиеся параметры, определяющие квантовое состояние такой системы? Мой ответ прост. Нет, никогда. "

Кандидаты на физическую реализацию

Дополнительная информация: Список предлагаемых квантовых регистров.

Практический квантовый компьютер должен использовать физическую систему в качестве программируемого квантового регистра. Исследователи изучают несколько технологий в качестве кандидатов на надежную реализацию кубитов. Сверхпроводники и захваченные ионы — одни из наиболее разработанных предложений, но экспериментаторы рассматривают и другие аппаратные возможности.

Теория

Вычислимость

Дополнительная информация: Теория вычислимости.

Любая вычислительная задача , решаемая классическим компьютером, также может быть решена и квантовым компьютером. Интуитивно это происходит потому, что считается, что все физические явления, включая работу классических компьютеров, можно описать с помощью квантовой механики , которая лежит в основе работы квантовых компьютеров.

И наоборот, любая задача, решаемая квантовым компьютером, также может быть решена и классическим компьютером. Можно смоделировать как квантовые, так и классические компьютеры вручную, используя всего лишь бумагу и ручку, если уделить достаточно времени. Более формально, любой квантовый компьютер можно смоделировать с помощью машины Тьюринга . Другими словами, квантовые компьютеры не предоставляют никаких дополнительных возможностей по сравнению с классическими компьютерами с точки зрения вычислительности . Это означает, что квантовые компьютеры не могут решать неразрешимые проблемы, такие как проблема остановки , и существование квантовых компьютеров не опровергает тезис Чёрча-Тьюринга .

Сложность

Основная статья: Квантовая теория сложности

Хотя квантовые компьютеры не могут решить проблемы, которые уже не могут решить классические компьютеры, есть подозрение, что они могут решать некоторые проблемы быстрее, чем классические компьютеры. Например, известно, что квантовые компьютеры могут эффективно факторизовать целые числа , хотя считается, что это не относится к классическим компьютерам.

Класс задач , которые могут быть эффективно решены с помощью квантового компьютера с ограниченной ошибкой, называется BQP , что означает «ограниченная ошибка, квантовое, полиномиальное время». Более формально, BQP — это класс задач, которые могут быть решены с помощью квантовой машины Тьюринга с полиномиальным временем и вероятностью ошибки не более 1/3. Как класс вероятностных задач, BQP является квантовым аналогом BPP («ограниченная ошибка, вероятностное, полиномиальное время»), класса проблем, которые могут быть решены вероятностными машинами Тьюринга с полиномиальным временем и ограниченной ошибкой. Известно, что ${\mathsf {BPP\subseteq BQP}}$ и широко подозревается, что ${\mathsf {BQP\subsetneq BPP}}$Это интуитивно означало бы, что квантовые компьютеры более мощны, чем классические компьютеры, с точки зрения временной сложности .

Предполагаемая связь BQP с несколькими классическими классами сложности.

Точная связь BQP с P , NP и PSPACE неизвестна. Однако известно, что ${\mathsf {P\subseteq BQP\subseteq PSPACE}}$; то есть все проблемы, которые могут быть эффективно решены с помощью детерминированного классического компьютера, также могут быть эффективно решены с помощью квантового компьютера, и все проблемы, которые могут быть эффективно решены с помощью квантового компьютера, также могут быть решены с помощью детерминированного классического компьютера с полиномиальными пространственными ресурсами. . Кроме того, предполагается, что BQP является строгим надмножеством P, а это означает, что существуют проблемы, которые эффективно решаются квантовыми компьютерами, но не могут быть эффективно решены детерминированными классическими компьютерами. Например, известно, что факторизация целых чисел и задача дискретного логарифма входят в BQP и предположительно находятся за пределами P. О взаимосвязи BQP и NP мало что известно, кроме того факта, что некоторые задачи NP, которые, как полагают, не входят в P. P также находятся в BQP (например, целочисленная факторизация и задача дискретного логарифма находятся в NP). Есть подозрение, что ${\mathsf {NP\nsubseteq BQP}}$; то есть считается, что существуют эффективно проверяемые проблемы, которые невозможно эффективно решить с помощью квантового компьютера. Как прямое следствие этого убеждения также предполагается, что BQP не пересекается с классом NP-полных следовало бы задач (если бы NP-полная задача находилась в BQP, то из NP-трудности , что все задачи в NP находятся в БКП).

См. также

• D-Wave Systems - канадская компания по квантовым вычислениям
• Электронная квантовая голография
• Глоссарий квантовых вычислений
• IARPA – Страницы американского правительственного агентства с кратким описанием целей перенаправления.
• IonQ — американская компания информационных технологий.
• Список новых технологий : новые технологии активно разрабатываются.
• Список квантовых процессоров - Список компонентов квантового компьютера
• Дистилляция магического состояния - алгоритм квантовых вычислений
• Естественные вычисления - введена терминология, охватывающая три класса методов. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Оптические вычисления - компьютер, использующий фотоны или световые волны.
• Квантовая шина - устройство, которое можно использовать для хранения или передачи информации между независимыми кубитами в квантовом компьютере. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Квантовое познание - применение квантовой механики к когнитивным явлениям. Страницы, отображающие описания из Викиданных в качестве запасного варианта.
• Квантовый объем - показатель возможностей квантового компьютера.
• Квантовая странность – неинтуитивные аспекты квантовой механики
• Rigetti Computing - американская компания по квантовым вычислениям.
• Суперкомпьютер - тип чрезвычайно мощного компьютера.
• Теоретическая информатика - раздел информатики и математики.
• Нетрадиционные вычисления - вычисления новыми или необычными методами.
• Valleytronics - Экспериментальная область в области полупроводников

Источники

• Ааронсон, Скотт (2013). Квантовые вычисления со времен Демокрита . Издательство Кембриджского университета. дои : 10.1017/CBO9780511979309 . ISBN  978-0-521-19956-8 . OCLC   829706638 .
• Ворчишь, Эмили; Горовиц, Марк, ред. (2019). Квантовые вычисления: прогресс и перспективы . Вашингтон, округ Колумбия: Издательство национальных академий. дои : 10.17226/25196 . ISBN  978-0-309-47970-7 . ОСЛК   1091904777 . S2CID   125635007 .
• Мермин, Н. Дэвид (2007). Квантовая информатика: Введение . дои : 10.1017/CBO9780511813870 . ISBN  978-0-511-34258-5 . OCLC   422727925 .
• Нильсен, Майкл ; Чуанг, Исаак (2010). Квантовые вычисления и квантовая информация (изд. к 10-летию). дои : 10.1017/CBO9780511976667 . ISBN  978-0-511-99277-3 . OCLC   700706156 . S2CID   59717455 .
• Шор, Питер В. (1994). Алгоритмы квантовых вычислений: дискретные логарифмы и факторинг . Симпозиум по основам информатики . Санта-Фе, Нью-Мексико : IEEE . стр. 124–134. дои : 10.1109/SFCS.1994.365700 . ISBN  978-0-8186-6580-6 .

Дальнейшее чтение

Учебники

• Акама, Сэйки (2014). Элементы квантовых вычислений: история, теории и инженерные приложения . Спрингер. дои : 10.1007/978-3-319-08284-4 . ISBN  978-3-319-08284-4 . OCLC   884786739 .
• Бененти, Джулиано; Казати, Джулио; Россини, Давиде; Стрини, Джулиано (2019). Принципы квантовых вычислений и информации: комплексный учебник (2-е изд.). дои : 10.1142/10909 . ISBN  978-981-3237-23-0 . OCLC   1084428655 . S2CID   62280636 .
• Бернхардт, Крис (2019). Квантовые вычисления для всех . МТИ Пресс. ISBN  978-0-262-35091-4 . OCLC   1082867954 .
• Хидари, Джек Д. (2021). Квантовые вычисления: прикладной подход (2-е изд.). дои : 10.1007/978-3-030-83274-2 . ISBN  978-3-03-083274-2 . OCLC   1272953643 . S2CID   238223274 .
• Хироши, Имаи; Масахито, Хаяси, ред. (2006). Квантовые вычисления и информация: от теории к эксперименту . Темы прикладной физики. Том. 102. дои : 10.1007/3-540-33133-6 . ISBN  978-3-540-33133-9 .
• Хьюз, Кьяран; Исааксон, Джошуа; Перри, Анастасия; Сан, Ранбель Ф.; Тернер, Джессика (2021). Квантовые вычисления для квантовых любознательных (PDF) . дои : 10.1007/978-3-030-61601-4 . ISBN  978-3-03-061601-4 . OCLC   1244536372 . S2CID   242566636 .
• Джагер, Грегг (2007). Квантовая информация: обзор . дои : 10.1007/978-0-387-36944-0 . ISBN  978-0-387-36944-0 . OCLC   186509710 .
• Джонстон, Эрик Р.; Харриган, Ник; Химено-Сеговия, Мерседес (2019). Программирование квантовых компьютеров: основные алгоритмы и примеры кода . О'Рейли Медиа, Инкорпорейтед. ISBN  978-1-4920-3968-6 . OCLC   1111634190 .
• Кэй, Филипп; Лафламм, Раймонд ; Моска, Мишель (2007). Введение в квантовые вычисления . ОУП Оксфорд. ISBN  978-0-19-857000-4 . OCLC   85896383 .
• Китаев, Алексей Юрьевич. ; Шен, Александр Х.; Вялый, Михаил Н. (2002). Классические и квантовые вычисления . Американское математическое соц. ISBN  978-0-8218-3229-5 . OCLC   907358694 .
• Штольце, Иоахим; Сутер, Дитер (2004). Квантовые вычисления: краткий курс от теории к эксперименту . дои : 10.1002/9783527617760 . ISBN  978-3-527-61776-0 . OCLC   212140089 .
• Сасскинд, Леонард ; Фридман, Искусство (2014). Квантовая механика: теоретический минимум . Нью-Йорк : Основные книги . ISBN  978-0-465-08061-8 .
• Вихерт, Андреас (2020). Принципы квантового искусственного интеллекта: квантовое решение задач и машинное обучение (2-е изд.). дои : 10.1142/11938 . ISBN  978-981-12-2431-7 . OCLC   1178715016 . S2CID   225498497 .
• Вонг, Томас (2022). Введение в классические и квантовые вычисления (PDF) . Корневая роща. ISBN  979-8-9855931-0-5 . OCLC   1308951401 . Архивировано из оригинала (PDF) 29 января 2022 года . Проверено 6 февраля 2022 г.
• Бэй, Се; Чжоу, Дуань материей . встречается с квантовой Цзэн , - Лу ; информация Квантовая  978-1-4939-9084-9 . OCLC   1091358969 . S2CID   118528258 .

Научные

• Эббот, Дерек ; Деринг, Чарльз Р .; Кейвс, Карлтон М .; Лидар, Дэниел М .; Брандт, Ховард Э .; и др. (2003). «Мечты против реальности: пленарные дебаты по квантовым вычислениям». Квантовая обработка информации . 2 (6): 449–472. arXiv : Quant-ph/0310130 . дои : 10.1023/B:QINP.0000042203.24782.9a . hdl : 2027.42/45526 . S2CID   34885835 .
• Бертьям, Андре (1 декабря 1998 г.). «Квантовые вычисления». Руководство по решению квантовой механики . стр. 233–234. дои : 10.1142/9789814541893_0016 . ISBN  978-981-4541-88-6 . S2CID   128255429 – через Semantic Scholar.
• ДиВинченцо, Дэвид П. (2000). «Физическая реализация квантовых вычислений». Fortschritte der Physik . 48 (9–11): 771–783. arXiv : Quant-ph/0002077 . Бибкод : 2000ForPh..48..771D . doi : 10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E . S2CID   15439711 .
• ДиВинченцо, Дэвид П. (1995). «Квантовые вычисления». Наука . 270 (5234): 255–261. Бибкод : 1995Sci...270..255D . CiteSeerX   10.1.1.242.2165 . дои : 10.1126/science.270.5234.255 . S2CID   220110562 . В таблице 1 указано время переключения и дефазировки для различных систем.
• Фейнман, Ричард (1982). «Моделирование физики с помощью компьютеров». Международный журнал теоретической физики . 21 (6–7): 467–488. Бибкод : 1982IJTP...21..467F . CiteSeerX   10.1.1.45.9310 . дои : 10.1007/BF02650179 . S2CID   124545445 .
• Ютнер, Валентин (2021). «Квантовый императив: решение юридических вопросов квантовых компьютеров» . Мораль и машины . 1 (1): 52–59. дои : 10.5771/2747-5174-2021-1-52 . S2CID   236664155 .
• Кранц, П.; Кьергаард, М.; Ян, Ф.; Орландо, штат Калифорния; Густавссон, С.; Оливер, штат Вашингтон (17 июня 2019 г.). «Руководство квантового инженера по сверхпроводящим кубитам». Обзоры прикладной физики . 6 (2): 021318. arXiv : 1904.06560 . Бибкод : 2019АпПРв...6б1318К . дои : 10.1063/1.5089550 . ISSN   1931-9401 . S2CID   119104251 .
• Митчелл, Ян (1998). «Вычислительная мощность в 21 веке: закон Мура и не только» .
• Саймон, Дэниел Р. (1994). «О возможностях квантовых вычислений» . Институт инженеров по электротехнике и электронике Computer Society Press.

Внешние ссылки

• СМИ, связанные с квантовым компьютером, на Викискладе?
• Учебные материалы по квантовым вычислениям в Викиверситете
• Стэнфордская энциклопедия философии : « Квантовые вычисления » Амита Хагара и Майкла Э. Каффаро.
• «Квантовые вычисления, теория» , Энциклопедия математики , EMS Press , 2001 [1994]
• Квантовые вычисления для очень любопытных Энди Матущак и Майкл Нильсен

Лекции

• Квантовые вычисления для решительных — 22 видеолекции Майкла Нильсена
• Видеолекции Дойча Дэвида
• Лекции в Институте Анри Пуанкаре (слайды и видео)
• Онлайн-лекция «Введение в квантовые вычисления», Эдвард Герджуой (2008 г.)
• Ломонако, Сэм. Четыре лекции по квантовым вычислениям, прочитанные в Оксфордском университете в июле 2006 г.