Зарядный кубит

Принципиальная схема цепи зарядового кубита. Остров (пунктирная линия) образован сверхпроводящим электродом между конденсатором затвора и емкостью перехода.

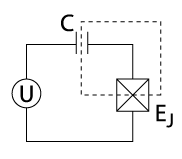
В квантовых вычислениях зарядовый кубит (также известный как ящик куперовской пары ) — это кубит , базисные состояния которого являются состояниями заряда (т. е. состояниями, которые отражают наличие или отсутствие избыточных куперовских пар на острове). В сверхпроводящих квантовых вычислениях зарядовый кубит образован крошечным сверхпроводящим островком, соединенным джозефсоновским переходом (или практически сверхпроводящим туннельным переходом ) со сверхпроводящим резервуаром (см. рисунок). Состояние кубита определяется количеством куперовских пар, туннелировавших через переход. В отличие от зарядового состояния атомного или молекулярного иона, зарядовые состояния такого «острова» включают макроскопическое число электронов проводимости острова. Квантовая суперпозиция зарядовых состояний может быть достигнута путем настройки напряжения на затворе U , которое управляет химическим потенциалом острова. Зарядовый кубит обычно считывается путем электростатического соединения острова с чрезвычайно чувствительным электрометром, таким как радиочастотный одноэлектронный транзистор .

Типичное T ₂ время когерентности для зарядового кубита составляет порядка 1–2 мкс. Недавняя работа показала, что T ₂ раза приближается к 100 мкс при использовании типа зарядового кубита, известного как трансмон, внутри трехмерной сверхпроводящей полости. Понимание пределов Т ₂ является активной областью исследований в области сверхпроводящих квантовых вычислений .

Изготовление

Зарядовые кубиты изготавливаются с использованием технологий, аналогичных тем, которые используются в микроэлектронике . Устройства обычно изготавливаются на кремниевых или сапфировых пластинах с использованием электронно-лучевой литографии (отличной от фазового кубита , в которой используется фотолитография ) и процессов испарения металлических тонких пленок. Для создания джозефсоновских переходов метод, известный как теневое испарение обычно используется ; это включает в себя испарение исходного металла поочередно под двумя углами через определенную литографией маску в электронно-лучевом резисте. В результате образуются два перекрывающихся слоя сверхпроводящего металла, между которыми тонкий слой изолятора (обычно оксида алюминия осаждается ).

гамильтониан

Если переход Джозефсона имеет емкость перехода $C_{\rm {J}}$и конденсатор затвора $C_{\rm {g}}$, то зарядовая (кулоновская) энергия одной куперовской пары равна:

$E_{\rm {C}}=(2e)^{2}/2(C_{\rm {g}}+C_{\rm {J}}).$

Если $n$ обозначает количество избыточных куперовских пар на острове (т.е. его чистый заряд равен $-2ne$), то гамильтониан:

$H=\sum _{n}{\big [}E_{\rm {C}}(n-n_{\rm {g}})^{2}|n\rangle \langle n|-{\frac {1}{2}}E_{\rm {J}}(|n\rangle \langle n+1|+|n+1\rangle \langle n|){\big ]},$

где $n_{\rm {g}}=C_{\rm {g}}V_{\rm {g}}/(2e)$ – это параметр управления, известный как эффективный компенсационный заряд ( $V_{\rm {g}}$ - напряжение затвора), и $E_{\rm {J}}$ джозефсоновская энергия туннельного перехода.

При низкой температуре и низком напряжении на затворе можно ограничить анализ только самым низким напряжением. $n=0$ и $n=1$ состояний и, следовательно, получить двухуровневую квантовую систему (она же кубит ).

Обратите внимание, что некоторые недавние статьи примите другие обозначения и определите энергию заряда как энергию одного электрона:

$E_{\rm {C}}=e^{2}/2(C_{\rm {g}}+C_{\rm {J}}),$

и тогда соответствующий гамильтониан:

$H=\sum _{n}{\big [}4E_{\rm {C}}(n-n_{\rm {g}})^{2}|n\rangle \langle n|-{\frac {1}{2}}E_{\rm {J}}(|n\rangle \langle n+1|+|n+1\rangle \langle n|){\big ]}.$

Преимущества

На сегодняшний день наиболее успешными реализациями кубитов являются ионные ловушки и ЯМР , а алгоритм Шора даже реализуется с использованием ЯМР. Однако трудно представить, чтобы эти два метода были масштабированы до сотен, тысяч или миллионов кубитов, необходимых для создания квантового компьютера . Твердотельные представления кубитов гораздо легче масштабируются, но у них самих есть своя проблема: декогеренция . Однако сверхпроводники имеют то преимущество, что их легче масштабировать, и они более когерентны, чем обычные твердотельные системы.

успехи

Реализация сверхпроводящих зарядовых кубитов быстро продвигалась с 1996 года. Конструкция была теоретически описана в 1997 году Шнирманом, в то время как доказательства квантовой когерентности заряда в ящике куперовской пары были опубликованы в феврале 1997 года Винсентом Бушиа и др. В 1999 году когерентные колебания заряда Кубита были впервые обнаружены Накамурой и др. Манипулирование квантовыми состояниями и полная реализация зарядового кубита наблюдались 2 года спустя. в 2007 году в Йельском университете было разработано более совершенное устройство, известное как Transmon, демонстрирующее увеличенное время когерентности благодаря пониженной чувствительности к зарядовому шуму. В 2007 году в Йельском университете Робертом Дж. Шёлкопфом , Мишелем Деворе , Стивеном М. Гирвином и их коллегами