Торический код

Торический код — это топологический квантовый код, исправляющий ошибки , и пример кода стабилизатора , определенного на двумерной спиновой решетке . Это самая простая и наиболее хорошо изученная из моделей квантового двойника. Это также простейший пример топологического порядка — Z2 _. топологический порядок (впервые изучено в контексте Z ₂ спиновой жидкости в 1991 году). Торический код также можно рассматривать как Z ₂ решеточную калибровочную теорию в определенном пределе. Его представил Алексей Китаев .

Торический код получил свое название от периодических граничных условий, придающих ему форму тора . Эти условия придают модели трансляционную инвариантность, что полезно для аналитического исследования. Однако некоторые экспериментальные реализации требуют открытых граничных условий, позволяющих встроить систему в двумерную поверхность. Результирующий код обычно известен как планарный код. В большинстве, но не во всех случаях, это поведение идентично торическому коду.

Исправление ошибок и расчет

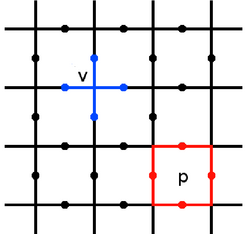
Торический код определяется на двумерной решетке, обычно выбираемой в качестве квадратной решетки , со спина ½, степенью свободы расположенной на каждом ребре. Они выбраны периодическими. Операторы стабилизатора определены на спинах вокруг каждой вершины. $v$ и плакетка (или грань, т.е. вершина двойственной решетки) $p$ решетки следующим образом:

$A_{v}=\prod _{i\in v}\sigma _{i}^{x},\,\,B_{p}=\prod _{i\in p}\sigma _{i}^{z}.$

Где здесь мы используем $i\in v$ для обозначения ребер, касающихся вершины $v$, и $i\in p$ для обозначения краев, окружающих плакетку $p$. Пространство стабилизаторов кода — это то пространство, в котором все стабилизаторы действуют тривиально, следовательно, для любого состояния $|\psi \rangle$ в этом пространстве считается, что

$A_{v}|\psi \rangle =|\psi \rangle ,\,\,\forall v,\,\,B_{p}|\psi \rangle =|\psi \rangle ,\,\,\forall p.$

Для торического кода это пространство является четырехмерным и поэтому может использоваться для хранения двух кубитов квантовой информации . Это можно доказать, рассмотрев количество независимых операторов стабилизатора. Возникновение ошибок приведет к перемещению состояния из пространства стабилизатора, в результате чего появятся вершины и плакеты, для которых вышеуказанное условие не выполняется. С позиций этих нарушений является синдромом кода, который можно использовать для исправления ошибок.

Часть торического кода. Выделены вершина и плакетка, а также вращения, использованные при определении их стабилизаторов.

Уникальная природа топологических кодов, таких как торический код, заключается в том, что нарушения стабилизатора можно интерпретировать как квазичастицы . В частности, если код находится в состоянии $|\phi \rangle$ такой, что,

$A_{v}|\phi \rangle =-|\phi \rangle$,

квазичастица, известная как $e$ можно сказать, что любой из них существует в вершине $v$. Аналогичным образом нарушения $B_{p}$ связаны с так называемыми $m$ анионы на плакетках. Таким образом, пространство стабилизатора соответствует анонному вакууму. Одиночные ошибки спина приводят к созданию пар анионов и их транспортировке по решетке.

Когда ошибки создают анионные пары и перемещают анионы, можно представить путь, соединяющий их, состоящий из всех задействованных ссылок. Если затем анионы встречаются и уничтожаются, этот путь описывает петлю. Если цикл топологически тривиален, он не влияет на хранимую информацию. В этом случае уничтожение анионов исправляет все ошибки, связанные с их созданием и транспортировкой. Однако, если цикл топологически нетривиален, хотя повторное уничтожение анионов возвращает состояние в пространство стабилизатора, он также реализует логическую операцию над хранимой информацией. Поэтому ошибки в данном случае не исправляются, а консолидируются.

Топологически нетривиальные петли тора. Перемещение анионов вдоль них реализует логические операторы Паули для хранимых кубитов.

Рассмотрим модель шума, для которой битовые и фазовые ошибки возникают независимо на каждом вращении, обе с вероятностью p . Когда p мало, это приведет к созданию редко распределенных пар анионов, которые не ушли далеко от точки своего создания. Исправление может быть достигнуто путем идентификации пар, в которых были созданы анионы (вплоть до класса эквивалентности), а затем их повторного уничтожения для устранения ошибок. Однако по мере увеличения p становится все более двусмысленным вопрос о том, как можно спарить анионы без риска образования топологически нетривиальных петель. Это дает пороговую вероятность, при которой исправление ошибок почти наверняка будет успешным. Путем сопоставления с моделью Изинга со случайными связями было обнаружено, что эта критическая вероятность составляет около 11%.

Можно также рассмотреть другие модели ошибок и найти пороговые значения. Во всех изученных до сих пор случаях было обнаружено, что код насыщает границу хеширования . Для некоторых моделей ошибок, таких как смещенные ошибки, где битовые ошибки возникают чаще, чем фазовые ошибки, или наоборот, для достижения оптимальных пороговых значений необходимо использовать решетки, отличные от квадратной.

Эти пороговые значения являются верхними пределами и бесполезны, если не найдены эффективные алгоритмы для их достижения. Наиболее часто используемый алгоритм — идеальное сопоставление минимального веса . При применении к модели шума с независимыми битовыми и флип-ошибками достигается порог около 10,5%. Это лишь немного меньше максимального показателя в 11%. Однако согласование не работает так хорошо, когда существуют корреляции между битовыми и фазовыми ошибками, например, при деполяризующем шуме.

Рассмотрены средства выполнения квантовых вычислений над логической информацией, хранящейся в торическом коде, при этом свойства кода обеспечивают отказоустойчивость. Было показано, что расширение пространства стабилизатора с помощью «дыр», вершин или плакеток, на которых стабилизаторы не применяются, позволяет закодировать в коде множество кубитов. Однако универсальный набор унитарных вентилей не может быть отказоустойчиво реализован с помощью унитарных операций, поэтому для достижения квантовых вычислений требуются дополнительные методы. Например, универсальные квантовые вычисления могут быть достигнуты путем подготовки магических состояний с помощью закодированных квантовых заглушек, называемых tidBits, которые используются для телепортации в необходимые дополнительные ворота при замене кубитами. Более того, подготовка магических состояний должна быть отказоустойчивой, чего можно достичь путем дистилляции магических состояний на зашумленных магических состояниях. на этом принципе схема Была найдена основанная квантовых вычислений, порог ошибки которой является самым высоким из известных для двумерной архитектуры.

самокоррекция

Поскольку операторы стабилизатора торического кода квазилокальны и действуют только на спины, расположенные рядом друг с другом на двумерной решетке, вполне реально определить следующий гамильтониан:

$H_{\rm {TC}}=-J\sum _{v}A_{v}-J\sum _{p}B_{p},\,\,\,J>0.$

Основное пространство состояний этого гамильтониана является пространством стабилизатора кода. Возбужденные состояния соответствуют состояниям анионов, энергия которых пропорциональна их числу. Таким образом, локальные ошибки энергетически подавляются зазором, который, как было показано, устойчив к локальным возмущениям. Однако динамические эффекты таких возмущений по-прежнему могут вызывать проблемы в коде.

Этот пробел также придает коду определенную устойчивость к термическим ошибкам, позволяя почти наверняка исправить его в течение определенного критического времени. Это время увеличивается с $J$, но поскольку произвольное увеличение этой связи нереально, защита, обеспечиваемая гамильтонианом, все еще имеет свои пределы.

Часто рассматриваются способы превращения торического кода или планарного кода в полностью самокорректирующуюся квантовую память. Самокоррекция означает, что гамильтониан естественным образом будет подавлять ошибки на неопределенный срок, что приведет к тому, что время жизни будет отклоняться от термодинамического предела. Было обнаружено, что в торическом коде это возможно только при наличии дальнодействующих взаимодействий между анионами. Сделаны предложения по реализации их в лаборатории. Другой подход — обобщение модели на более высокие измерения с возможностью самокоррекции в 4D только с квазилокальными взаимодействиями.

Любая модель

Как уже говорилось выше, так называемые $e$ и $m$ квазичастицы связаны с вершинами и плакетками модели соответственно. Эти квазичастицы можно назвать анионами из-за нетривиального эффекта их сплетения. В частности, хотя оба вида анионов бозонны относительно самих себя, сплетение двух $e$или $m$не имеет никакого эффекта, полная монодромия $e$ и $m$ приведет к фазе $-1$. Такой результат не согласуется ни с бозонной , ни с фермионной статистикой и, следовательно, является анионным.

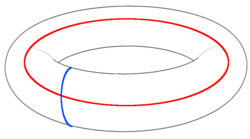
Анонная взаимная статистика квазичастиц демонстрирует логические операции, выполняемые топологически нетривиальными циклами. Рассмотрим создание пары $e$ анионы с последующей транспортировкой одного из них по топологически нетривиальной петле, такой как показанная на торе синим цветом на рисунке выше, прежде чем пара будет повторно аннилирована. Состояние возвращается в пространство стабилизатора, но цикл реализует логическую операцию над одним из сохраненных кубитов. Если $m$ Анионы аналогичным образом перемещаются через красный цикл выше, что также приведет к логической операции. Этап $-1$ Полученный при сплетении анионов показывает, что эти операции не коммутируют, а антикоммутируют. Поэтому их можно интерпретировать как логические. $Z$ и $X$ Операторы Паули на одном из хранимых кубитов. Соответствующие логические числа Паули на другом кубите соответствуют $m$ любой, кто следует за синей петлей и $e$ любой, кто следует за красным. Никакого переплетения не происходит, когда $e$ и $m$ проходят параллельными путями, фаза $-1$ поэтому не возникает и соответствующие логические операции коммутируют. Этого и следовало ожидать, поскольку эти операции формируют операции, действующие на разные кубиты.

В связи с тем, что оба $e$ и $m$ анионы могут создаваться парами, ясно видеть, что обе эти квазичастицы являются своими собственными античастицами. Сложная частица, состоящая из двух $e$ Таким образом, анионы эквивалентны вакууму, поскольку вакуум может дать такую ​​пару, и такая пара аннигилирует в вакууме. Соответственно, эти композиты обладают бозонной статистикой, поскольку их сплетение всегда совершенно тривиально. Композиция из двух $m$ анионы аналогично вакууму. Создание таких композитов известно как слияние анионов, и результаты могут быть записаны в терминах правил слияния. В данном случае они принимают вид

$e\times e=1,\,\,\,m\times m=1.$

Где $1$ обозначает вакуум. Составная часть $e$ и $m$ не является тривиальным. Таким образом, это представляет собой еще одну квазичастицу в модели, иногда обозначаемую $\psi$, с правилом слияния,

$e\times m=\psi .$

Из статистики переплетения анионов мы видим, что, поскольку любой единичный обмен двух $\psi$'s будет включать в себя полную монодромию составляющего $e$ и $m$, фаза $-1$ будет результат. Это подразумевает фермионную самостатистику для $\psi$х.

Обобщения

Для формирования кода исправления ошибок использование тора не требуется. Могут быть использованы и другие поверхности, топологические свойства которых определяют вырождение пространства стабилизатора. В общем, коды с квантовой коррекцией ошибок, определенные на двумерных спиновых решетках в соответствии с вышеизложенными принципами, известны как поверхностные коды.

Также возможно определить подобные коды, используя спины более высокой размерности. Это модели квантового двойника и струнно-сетевые модели, которые обеспечивают большее разнообразие поведения анионов и поэтому могут использоваться для более продвинутых квантовых вычислений и предложений по исправлению ошибок. К ним относятся не только модели с абелевыми анионами, но и модели с неабелевой статистикой.

прогресс

Наиболее явная демонстрация свойств торического кода была продемонстрирована в подходах, основанных на состояниях. Вместо того, чтобы пытаться реализоватьГамильтониан, они просто подготавливают код в пространстве стабилизатора. Используя эту технику, эксперименты смогли продемонстрировать создание, транспортировку и статистику анионов. и измерение топологической энтропии запутанности . Более поздние эксперименты также смогли продемонстрировать свойства кода по исправлению ошибок.

Для реализации торического кода и его обобщений с помощью гамильтониана большой прогресс был достигнут с использованием джозефсоновских переходов . Теория реализации гамильтонианов разработана для широкого класса топологических кодов. Также был проведен эксперимент, реализовавший гамильтониан торического кода для небольшой решетки и продемонстрировавший квантовую память, обеспечиваемую ее вырожденным основным состоянием.

Другие теоретические и экспериментальные работы, направленные на реализацию, основаны на холодных атомах. Исследован набор методов, которые можно использовать для реализации топологических кодов с помощью оптических решеток. как и эксперименты, касающиеся минимальных случаев топологического порядка. Такие минимальные экземпляры торического кода были реализованы экспериментально на изолированных квадратных плакетках. прогресс Также наблюдается в моделировании торической модели с ридберговскими атомами , в котором можно продемонстрировать гамильтониан и эффекты диссипативного шума. Эксперименты с массивами атомов Ридберга также успешно реализовали торический код с периодическими граничными условиями в двух измерениях путем когерентной транспортировки массивов запутанных атомов.

Внешние ссылки

• https://skepsisfera.blogspot.com/2010/04/kitaevs-toric-code.html