Квантовый секрет обмена

Совместное использование квантового секрета ( QSS ) — это квантовая криптографическая схема для безопасной связи , выходящая за рамки простого квантового распределения ключей . Он модифицирует классическую схему совместного использования секретов (CSS), используя квантовую информацию и теорему о запрете клонирования для достижения максимальной безопасности связи.

Метод разделения секрета заключается в том, что отправитель желает поделиться секретом с несколькими сторонами-получателями таким образом, чтобы секрет был полностью раскрыт только в том случае, если достаточно большая часть получателей работает вместе. Однако, если недостаточно получателей будут работать вместе, чтобы раскрыть секрет, секрет останется полностью неизвестным.

Классическая схема была независимо предложена Ади Шамиром. и Джордж Блейкли в 1979 году. В 1998 году Марк Хиллери, Владимир Бужек и Андре Бертьяум расширили теорию, включив в нее использование квантовых состояний для создания безопасного ключа , который можно было бы использовать для передачи секрета через классические данные. В последующие годы была проделана дополнительная работа по распространению теории на передачу квантовой информации в качестве секрета, а не просто на использование квантовых состояний для установления криптографического ключа.

QSS было предложено использовать в квантовых деньгах а также для совместных текущих счетов , квантовых сетей и распределенных квантовых вычислений , среди других приложений.

Протокол

Самый простой случай: GHZ заявляет

Этот пример соответствует исходной схеме, предложенной Hillery et al. в 1998 году, в котором используются состояния Гринбергера-Хорна-Цайлингера (GHZ) . Вскоре после этого была разработана аналогичная схема, в которой вместо трехчастичных состояний использовались двухчастичные запутанные состояния. В обоих случаях протокол, по сути, является расширением распределения квантовых ключей на два получателя вместо одного.

Следуя общепринятому языку, пусть отправителя обозначим как Алиса , а двух получателей — Боб и Чарли. Цель Алисы — отправить каждому получателю «долю» ее секретного ключа (на самом деле просто квантового состояния) таким образом, чтобы:

1. Ни доля Боба, ни доля Чарли не содержат никакой информации об исходном сообщении Алисы, и поэтому ни одна из них не может раскрыть секрет самостоятельно.
2. Секрет можно раскрыть только в том случае, если Боб и Чарли будут работать вместе, и в этом случае секрет будет полностью раскрыт.
3. Присутствие внешнего подслушивателя или нечестного получателя (Боба или Чарли) может быть обнаружено без раскрытия секрета.

Алиса инициирует протокол, делясь с каждым из Боба и Чарли по одной частице из триплета GHZ в (стандартном) Z-базисе, сама удерживая третью частицу:

$|\mathrm {\Psi } \rangle _{\rm {GHZ}}={\frac {|000\rangle +|111\rangle }{\sqrt {2}}},$

где $|\mathrm {0} \rangle$ и $|\mathrm {1} \rangle$ являются ортогональными модами в произвольном гильбертовом пространстве .

После того, как каждый участник измеряет свою частицу в X- или Y-базисе (выбранном случайно), они делятся (через классический общедоступный канал ), какой базис они использовали для измерения, но не сам результат. Объединив результаты своих измерений, Боб и Чарли могут сделать вывод, что Алиса измеряла в 50% случаев. Повторяя этот процесс много раз и используя небольшую часть для проверки отсутствия злоумышленников, три участника могут создать общий ключ для безопасного общения. Рассмотрим следующее в качестве наглядного примера того, как это будет работать.

Определим собственные состояния x и y следующим стандартным способом:

$|\mathrm {+x} \rangle ={\frac {|0\rangle +|1\rangle }{\sqrt {2}}},|\mathrm {-x} \rangle ={\frac {|0\rangle -|1\rangle }{\sqrt {2}}}$

$|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}$.

Состояние GHZ тогда можно переписать как

$|\mathrm {\Psi } \rangle _{\rm {GHZ}}={\frac {1}{2{\sqrt {2}}}}[({|+x\rangle _{a}|+x\rangle _{b}+|-x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}+|1\rangle _{c})+({|+x\rangle _{a}|-x\rangle _{b}+|-x\rangle _{a}|+x\rangle _{b}})(|0\rangle _{c}-|1\rangle _{c})]$,

где (a, b, c) обозначают частицы для (Алисы, Боба, Чарли), а состояния Алисы и Боба записаны в X-базисе. Используя эту форму, очевидно, что существует корреляция между измерениями Алисы и Боба и одночастичным состоянием Чарли:

если у Алисы и Боба коррелирующие результаты, то у Чарли есть состояние ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ и если у Алисы и Боба есть антикоррелированные результаты, то у Чарли есть состояние ${\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}$.

Влияние измерений Алисы и Боба на состояние Чарли для стандартного триплета GHZ.

Из таблицы, суммирующей эти корреляции, ясно, что, зная основы измерения Алисы и Боба, Чарли может использовать свой собственный результат измерения, чтобы сделать вывод, были ли у Алисы и Боба одинаковые или противоположные результаты. Однако обратите внимание: чтобы сделать этот вывод, Чарли должен выбрать правильную основу измерения для измерения своей собственной частицы. Поскольку он случайным образом выбирает между двумя некоммутирующими базами, только в половине случаев он сможет извлечь полезную информацию. В другой половине случаев результаты должны быть отброшены. Кроме того, из таблицы видно, что Чарли не имеет возможности определить, кто что измерял, только если результаты Алисы и Боба были коррелированы или антикоррелированы. Таким образом, единственный способ для Чарли выяснить измерение Алисы — это работать вместе с Бобом и делиться своими результатами. При этом они смогут извлечь результаты Алисы для каждого измерения и использовать эту информацию для создания криптографического ключа, который будет известен только им.

(( k , n )) пороговая схема

Простой случай, описанный выше, можно расширить аналогично тому, как это сделали Шамир и Блейкли в CSS, с помощью схемы определения порога . В пороговой схеме (( k , n )) (двойные круглые скобки обозначают квантовую схему) Алиса разбивает свой секретный ключ (квантовое состояние) на n долей, так что для извлечения полной информации требуются любые k≤n долей, кроме k-1. или меньше акций не могут извлечь никакой информации о ключе Алисы.

Количество пользователей, необходимых для извлечения секрета, ограничено n /2 < k ≤ n . Рассмотрим для n ≥ 2 k , если пороговая схема (( k , n )) применяется к двум непересекающимся наборам k в n , то могут быть восстановлены две независимые копии секрета Алисы. Это, конечно, нарушит теорему о запрете клонирования, и именно поэтому n должно быть меньше 2k.

Пока (( k , n )) существует пороговая схема пороговая схема (( k , n -1)) может быть построена путем простого отбрасывания одной акции. Этот метод можно повторять до тех пор, пока k=n.

Ниже представлена ​​простая ((2,3)) пороговая схема: и более сложные схемы можно представить, увеличив количество долей, которые Алиса разделяет свое исходное состояние на:

Рассмотрим Алису, начиная с состояния одного кутрита.

$|\mathrm {\Psi } \rangle _{a}=\alpha |0\rangle +\beta |1\rangle +\gamma |2\rangle ,$

а затем сопоставить его с тремя кутритами

$|\mathrm {\psi } \rangle =\alpha (|000\rangle +|111\rangle +|222\rangle )+\beta (|012\rangle +|120\rangle +|201\rangle )+\gamma (|021\rangle +|102\rangle +|210\rangle )$

и совместное использование одного кутрита с каждым из трех приемников. Очевидно, что отдельная доля не дает никакой информации об исходном состоянии Алисы, поскольку каждая доля находится в максимально перемешанном состоянии. Однако две доли можно использовать для восстановления исходного состояния Алисы. Предположим, что первые две акции даны. Добавьте первую акцию ко второй (по модулю три), а затем прибавьте новую стоимость второй акции к первой. Результирующее состояние

$|\mathrm {\psi } \rangle =(\alpha |0\rangle +\beta |1\rangle +\gamma |2\rangle )(|00\rangle +|12\rangle +|21\rangle )$

где первый кутрит — это именно исходное состояние Алисы. С помощью этого метода исходное состояние отправителя может быть восстановлено на одной из частиц-получателей, но крайне важно, чтобы во время этого процесса восстановления не проводились никакие измерения, иначе любая суперпозиция внутри квантового состояния разрушится.

Безопасность

Безопасность QSS основана на теореме о запрете клонирования для защиты от возможных перехватчиков, а также от нечестных пользователей. В этом разделе используется протокол двухчастичной запутанности, кратко упомянутый выше.

Подслушивание

QSS обещает защиту от подслушивания точно так же, как и квантовое распределение ключей. Рассмотрим подслушивающую Еву, которая, как предполагается, способна идеально различать и создавать квантовые состояния, используемые в протоколе QSS. Цель Евы — перехватить одну из акций получателей (скажем, Боба), измерить ее, затем воссоздать состояние и отправить ее тому, кому эта доля изначально предназначалась. Проблема этого метода в том, что Еве нужно случайным образом выбрать основу для измерения, и в половине случаев она выберет неправильную основу. Когда она выберет правильный базис, она с уверенностью получит правильный результат измерения и сможет воссоздать измеренное ею состояние и отправить его Бобу без обнаружения ее присутствия. Однако, когда она выберет неверный базис, она в конечном итоге отправит одно из двух состояний с неверным базисом. Боб измерит состояние, которое она ему отправила, и в половине случаев это будет правильное определение, но только потому, что состояние из неправильного базиса представляет собой равную суперпозицию двух состояний в правильном базисе. Таким образом, в половине случаев, когда Ева измеряет неверную основу и, следовательно, отправляет неправильное состояние, Боб будет измерять неправильное состояние. Это вмешательство со стороны Евы приводит к возникновению ошибки в протоколе еще в 25% испытаний. Следовательно, при достаточном количестве измерений будет практически невозможно пропустить ошибки протокола, возникающие с вероятностью 75% вместо предсказанной теорией 50% вероятности, что сигнализирует о том, что в канале связи есть подслушиватель.

Более сложные стратегии подслушивания могут быть реализованы с использованием вспомогательных состояний, но подслушивающий все равно будет обнаружен аналогичным образом.

Нечестный участник

Теперь рассмотрим случай, когда один из участников протокола (скажем, Боб) действует как злонамеренный пользователь, пытаясь получить секрет без ведома других участников. Анализируя возможности, можно понять, что выбор правильного порядка, в котором Боб и Чарли публикуют свои базы измерений и результаты при проверке на подслушивание, может гарантировать обнаружение любого мошенничества, которое может иметь место. Правильный порядок оказывается следующим:

1. Приемник 1 публикует результаты измерений.
2. Приемник 2 публикует результаты измерений.
3. Приемник 2 выпускает базу измерений.
4. Приемник 1 освобождает базу измерения.

Такой порядок не позволяет получателю 2 узнать, какой базис использовать для обмана других участников, поскольку получатель 2 еще не знает, какой базис приемник 1 собирается объявить об использовании. Аналогичным образом, поскольку получатель 1 должен сначала опубликовать свои результаты, он не может контролировать, должны ли измерения быть коррелированными или антикоррелированными для допустимой комбинации используемых баз. Таким образом, нечестные действия приведут к ошибкам на этапе проверки перехватчика, независимо от того, является ли нечестный участник получателем 1 или получателем 2. Таким образом, порядок раскрытия данных должен быть тщательно выбран, чтобы не допустить, чтобы любой нечестный пользователь получил секрет, не будучи заметили другие участники.

Экспериментальная реализация

Этот раздел следует из первой экспериментальной демонстрации QSS в 2001 году, которая стала возможной благодаря достижениям в методах квантовой оптики .

Первоначальную идею QSS с использованием состояний GHZ было сложнее реализовать из-за трудностей в получении трехчастичных корреляций с помощью понижающего преобразования с процессов $\chi ^{3}$ нелинейности или трехфотонная аннигиляция позитрония, оба из которых являются редкими событиями. Вместо этого оригинальный эксперимент был проведен по двухчастичной схеме с использованием стандартного $\chi ^{2}$ Процесс спонтанного параметрического понижающего преобразования (SPDC), в котором третий коррелированный фотон является фотоном накачки.

Установка двухфотонного разделения квантового секрета (QSS) посредством спонтанного параметрического преобразования с понижением частоты (SPDC)

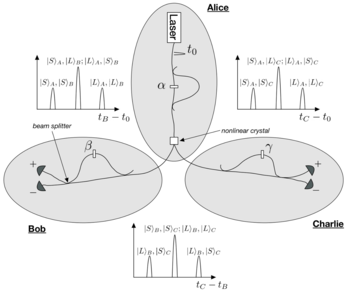
Экспериментальная установка работает следующим образом:

• Алиса: Импульсный лазер, излучаемый во времени. $t_{0}$ поступает в интерферометр с неравными длинами путей, так что накачка разделяется на два отдельных временных импульса с одинаковой амплитудой. Одно плечо интерферометра содержит фазовращатель для управления разностью фаз двух плеч, обозначенный $\alpha .$ Импульсы накачки фокусируются на нелинейном кристалле, где некоторые фотоны накачки преобразуются с понижением частоты в пары фотонов посредством SPDC. Затем пары SPDC разделяются: одна отправляется Бобу, а другая Чарли.
• Боб и Чарли: Оба приемника имеют интерферометры, идентичные тому, который использовала Алиса, так что достигается точно такая же разница во времени между двумя плечами, и каждый из них имеет фазовращатель, обозначаемый как $\beta$ для Боба и $\gamma$ для Чарли. Различные возможные траектории каждого интерферометра приводят к трем различным временным разницам между моментом испускания импульса накачки Алисы и моментом обнаружения фотонов SPDC Боба и Чарли ( $t_{B}$ и $t_{C}$, соответственно), а также три разницы во времени между обнаружениями на каждом из детекторов Боба и Чарли.

С использованием $|\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}$ где X и Y — это либо «S» для короткого пути, либо «L» для длинного пути, а i и j — одно из «A», «B» или «C» для обозначения интерферометра участника, это обозначение описывает произвольный путь. принимается для любой комбинации двух участников. Обратите внимание, что $|\mathrm {S} \rangle _{A},|\mathrm {L} \rangle _{j}$ и $|\mathrm {L} \rangle _{A},|\mathrm {S} \rangle _{j}$ где j представляет собой либо «B», либо «C», являются неразличимыми процессами, поскольку разница во времени между этими двумя процессами совершенно одинакова. То же самое верно для $|\mathrm {S} \rangle _{B},|\mathrm {S} \rangle _{C}$ и $|\mathrm {L} \rangle _{B},|\mathrm {L} \rangle _{C}.$ Описывая эти неразличимые процессы математически,

$|\mathrm {\psi } \rangle ={\frac {1}{\sqrt {2}}}(|L\rangle _{A},|S\rangle _{B}|S\rangle _{C}+e^{i(\alpha +\beta +\gamma )}|S\rangle _{A},|L\rangle _{B}|L\rangle _{C})),$

которое можно рассматривать как «псевдо-GHZ-состояние», в котором отличие от истинного состояния GHZ состоит в том, что три фотона не существуют одновременно. Тем не менее, тройные «совпадения» могут быть описаны точно той же функцией вероятности, что и для истинного состояния ГГЦ:

$P_{i,j,k}={\frac {1}{8}}(1+ijk\cos(\alpha +\beta +\gamma )),$

подразумевая, что QSS будет работать точно так же для этого двухчастичного источника.

Устанавливая фазы $\alpha ,\beta ,$ и $\gamma$ либо 0, либо ${\frac {\pi }{2}}$ во многом так же, как и двухфотонные тесты Белла , можно показать, что эта установка нарушает неравенство типа Белла для трех частиц:

$S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}$,

где $E(\alpha +\beta +\gamma )$ — это математическое ожидание для измерения совпадения с настройками фазовращателя. $(\alpha ,\beta ,\gamma )$. В этом эксперименте неравенство типа Белла было нарушено: $S_{\rm {exp}}=3.69$, что позволяет предположить, что эта установка демонстрирует квантовую нелокальность .

Этот плодотворный эксперимент показал, что квантовые корреляции в этой установке действительно описываются функцией вероятности $P_{i,j,k}.$ Простота источника SPDC допускала совпадения с гораздо большей частотой, чем традиционные источники трехфотонной запутанности, что делало QSS более практичным. Это был первый эксперимент, доказавший возможность протокола QSS.