Квантовая телепортация

Продолжительность: 26 секунд. 0:26

Схематическое видео, демонстрирующее отдельные этапы квантовой телепортации. Квантовое состояние Q отправляется от станции A к станции B с использованием пары запутанных частиц, созданных источником S. Станция A измеряет две свои частицы и передает результат на станцию ​​B, которая выбирает подходящее устройство на основе полученного сообщения. Благодаря действию устройства состояние частицы станции B переходит в Q.

Квантовая телепортация — это метод передачи квантовой информации от отправителя в одном месте к получателю на некотором расстоянии. Хотя в научной фантастике телепортация обычно изображается как средство перемещения физических объектов из одного места в другое, квантовая телепортация передает только квантовую информацию. Отправителю не обязательно знать конкретное передаваемое квантовое состояние. Более того, местоположение получателя может быть неизвестно, но для осуществления квантовой телепортации необходимо отправить классическую информацию от отправителя к получателю. Поскольку классическую информацию необходимо отправить, квантовая телепортация не может происходить быстрее скорости света.

Одна из первых научных статей, посвященных исследованию квантовой телепортации, - «Телепортация неизвестного квантового состояния через двойные классические каналы и каналы Эйнштейна-Подольского-Розена». опубликовано CH Bennett , G. Brassard , C. Crépeau , R. Jozsa , A. Peres и WK Wootters в 1993 году, в котором они предложили использовать методы двойной связи для отправки/получения квантовой информации. Он был экспериментально реализован в 1997 году двумя исследовательскими группами под руководством Санду Попеску и Антона Цайлингера соответственно.

Экспериментальные определения квантовой телепортации были сделаны в информационном содержании, включая фотоны, атомы, электроны и сверхпроводящие цепи , а также на расстоянии: 1400 км (870 миль) являются самым длинным расстоянием успешной телепортации, осуществленной Цзянь-Вэй Паня командой с использованием Спутник Мициус для космической квантовой телепортации.

Нетехническое резюме

В вопросах, касающихся квантовой теории информации , удобно работать с простейшей единицей информации: двухуровневой системой кубита . Кубит функционирует как квантовый аналог классической вычислительной части, бита , поскольку он может иметь измерительное значение как 0 , так и 1, тогда как классический бит может быть измерен только как 0 или 1. Квантовый двух- государственная система стремится передать квантовую информацию из одного места в другое, не теряя информацию и сохраняя качество этой информации. Этот процесс включает перемещение информации между носителями , а не перемещение самих носителей , аналогично традиционному процессу связи, поскольку две стороны остаются неподвижными во время передачи информации (цифровые носители, голос, текст и т. д.), в отличие от традиционного процесса связи. значение слова «телепорт».Основные компоненты, необходимые для телепортации, включают отправителя, информацию (кубит), традиционный канал, квантовый канал и получатель. Отправителю не обязательно знать точное содержание отправляемой информации. Постулат измерения квантовой механики – когда измерение производится над квантовым состоянием, любые последующие измерения «разрушатся» или что наблюдаемое состояние будет потеряно – создает навязывание телепортации: если отправитель производит измерение на своей информации, состояние может рухнуть, когда получатель получит информацию, поскольку состояние изменилось с момента, когда отправитель выполнил первоначальное измерение.

Интерактивное моделирование квантовой телепортации в виртуальной лаборатории от Quantum Flytrap. доступен онлайн . В этой оптической установке кубиты кодируются с использованием поляризации света . Телепортация происходит между фотоном-источником (установленным в произвольное состояние) и одним фотоном из запутанной пары. Измерение пары Белла выполняется на исходном фотоне и одном запутанном фотоне с использованием квантового вентиля CNOT , что дает два бита классической информации. целевой фотон затем вращается с помощью двух управляемых волновых пластин . На основе этой информации

Для реальной телепортации необходимо, чтобы было создано запутанное квантовое состояние для передачи кубита. Запутанность накладывает статистические корреляции между различными физическими системами, создавая или помещая две или более отдельных частиц в одно общее квантовое состояние. Это промежуточное состояние содержит две частицы, квантовые состояния которых связаны друг с другом: измерение состояния одной частицы дает информацию об измерении состояния другой частицы. Эти корреляции сохраняются даже тогда, когда измерения выбираются и выполняются независимо, вне причинного контакта друг с другом, как это было подтверждено в тестовых экспериментах Белла . Таким образом, наблюдение, являющееся результатом выбора измерения, сделанного в одной точке пространства-времени, кажется, мгновенно влияет на результаты в другой области, даже несмотря на то, что свет еще не успел пройти это расстояние, и этот вывод, по-видимому, противоречит специальной теории относительности . Это известно как парадокс ЭПР . Однако такие корреляции никогда не могут использоваться для передачи какой-либо информации со скоростью, превышающей скорость света. теорема об отсутствии связи . Таким образом, телепортация в целом никогда не может быть сверхсветовой , поскольку кубит не может быть реконструирован до тех пор, пока не поступит сопутствующая классическая информация.

Отправитель объединит частицу, о которой телепортируется информация, с одной из запутанных частиц, вызывая изменение общего запутанного квантового состояния. Частицы этого измененного состояния затем отправляются в анализатор, который измеряет изменение запутанного состояния. Измерение «изменения» позволит получателю воссоздать исходную информацию, имевшуюся у отправителя, в результате чего информация телепортируется или переносится между двумя людьми, находящимися в разных местах. Поскольку исходная квантовая информация «уничтожается», становясь частью состояния запутанности, теорема о запрете клонирования сохраняется, поскольку информация воссоздается из запутанного состояния, а не копируется во время телепортации.

Квантовый канал — это механизм связи, который используется для передачи всей квантовой информации и является каналом, используемым для телепортации (отношение квантового канала к традиционному каналу связи сродни кубиту, являющемуся квантовым аналогом классического бита). Однако в дополнение к квантовому каналу необходимо также использовать традиционный канал для сопровождения кубита, чтобы «сохранить» квантовую информацию. Когда производится измерение изменения между исходным кубитом и запутанной частицей, результат измерения должен передаваться по традиционному каналу, чтобы квантовая информация могла быть восстановлена, а приемник мог получить исходную информацию. Из-за необходимости использования традиционного канала скорость телепортации не может быть выше скорости света (следовательно, теорема об отсутствии связи не нарушается). Основным преимуществом этого является то, что состояния Белла можно передавать с помощью фотонов лазеров . , что делает телепортацию возможной через открытый космос, поскольку нет необходимости отправлять информацию по физическим кабелям или оптическим волокнам

Квантовые состояния могут быть закодированы в различных степенях свободы атомов. Например, кубиты могут быть закодированы в степенях свободы электронов, окружающих атомное ядро , или в степенях свободы самого ядра. Таким образом, для осуществления такого рода телепортации требуется запас атомов в принимающем пункте, доступный для запечатления на них кубитов.

По состоянию на 2015 год В качестве носителей информации использовались квантовые состояния одиночных фотонов, фотонные моды, одиночные атомы, атомные ансамбли, дефектные центры в твердых телах, одиночные электроны и сверхпроводящие цепи.

Понимание квантовой телепортации требует хороших знаний конечномерной линейной алгебры , гильбертовых пространств и матриц проекций . Кубит описывается с использованием двумерного комплексного . векторного пространства (гильбертова пространства), которое является основной основой для формальных манипуляций, приведенных ниже Практическое знание квантовой механики не является абсолютно необходимым для понимания математики квантовой телепортации, хотя без такого знания более глубокий смысл уравнений может оставаться весьма загадочным.

Протокол

Схема квантовой телепортации фотона

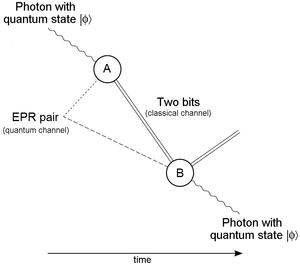
Ресурсы, необходимые для квантовой телепортации, — это канал связи , способный передавать два классических бита, средство генерации запутанного состояния Белла кубитов и его распределения в два разных места, выполнение измерения Белла на одном из кубитов состояния Белла и манипулирование квантовым состоянием Белла. состояние другого кубита из пары. Конечно, также должен быть какой-то входной кубит (в квантовом состоянии $|\phi \rangle$) телепортироваться. Тогда протокол : следующий

1. Состояние Белла генерируется, когда один кубит отправляется в местоположение A, а другой — в местоположение B.
2. Измерение Беллом кубита в состоянии Белла и кубита, который нужно телепортировать ( $|\phi \rangle$ ) выполняется в точке A. Это дает один из четырех результатов измерения, которые могут быть закодированы в двух классических битах информации. Оба кубита в позиции A затем отбрасываются.
3. Используя классический канал, два бита передаются от A к B. (Это единственный потенциально трудоемкий шаг после шага 1, поскольку передача информации ограничена скоростью света.)
4. В результате измерения, выполненного в точке A, кубит состояния Белла в точке B находится в одном из четырех возможных состояний. Из этих четырех возможных состояний одно идентично исходному квантовому состоянию. $|\phi \rangle$ , а остальные три тесно связаны между собой. Идентичность фактически полученного состояния кодируется двумя классическими битами и отправляется в местоположение B. Кубит состояния Белла в местоположении B затем модифицируется одним из трех способов или не модифицируется вообще, в результате чего получается кубит, идентичный кубиту состояния Белла в месте B. $|\phi \rangle$, состояние кубита, выбранного для телепортации.

Стоит отметить, что приведенный выше протокол предполагает, что кубиты адресуются индивидуально, а это означает, что кубиты различимы и физически помечены. Однако могут возникнуть ситуации, когда два одинаковых кубита неотличимы из-за пространственного перекрытия их волновых функций. При этом условии кубиты не могут индивидуально контролироваться или измеряться. Тем не менее, протокол телепортации, аналогичный описанному выше, все же может быть (условно) реализован путем использования двух независимо подготовленных кубитов без необходимости в начальном состоянии Белла. Это можно сделать, обращаясь к внутренним степеням свободы кубитов (например, спинам или поляризации) посредством пространственно локализованных измерений, выполняемых в отдельных областях A и B, где можно найти два пространственно перекрывающихся, неразличимых кубита. Это теоретическое предсказание было затем подтверждено экспериментально с помощью поляризованных фотонов в квантово-оптической установке.

и

Работа 1998 года подтвердила первоначальные предсказания. а расстояние телепортации было увеличено в августе 2004 года до 600 метров с использованием оптоволокна . Впоследствии рекордное расстояние квантовой телепортации было постепенно увеличено до 16 километров (9,9 миль). затем до 97 км (60 миль), и теперь составляет 143 км (89 миль) в ходе экспериментов под открытым небом на Канарских островах , проводимых между двумя астрономическими обсерваториями Канарского института астрофизики . Недавно был установлен рекорд (по состоянию на сентябрь 2015 г.) ) с использованием сверхпроводящих нанопроводных детекторов, которые достигли расстояния 102 км (63 мили) по оптическому волокну. Для материальных систем рекордное расстояние составляет 21 метр (69 футов).

Вариант телепортации, называемый телепортацией «открытого пункта назначения», с приемниками, расположенными в нескольких местах, был продемонстрирован в 2004 году с использованием пятифотонной запутанности. Также реализована телепортация составного состояния двух одиночных кубитов. В апреле 2011 года экспериментаторы сообщили, что они продемонстрировали телепортацию волновых пакетов света в полосе пропускания до 10 МГц, сохраняя при этом сильно неклассические состояния суперпозиции. В августе 2013 года сообщалось о достижении «полностью детерминированной» квантовой телепортации с использованием гибридной техники. 29 мая 2014 года ученые объявили о надежном способе передачи данных посредством квантовой телепортации. Квантовая телепортация данных осуществлялась и раньше, но весьма ненадежными методами. 26 февраля 2015 года ученые из Китайского университета науки и технологий в Хэфэе под руководством Чао-Яна Лу и Цзянь-Вэй Паня провели первый эксперимент по телепортации квантовой частицы с несколькими степенями свободы. Им удалось телепортировать квантовую информацию от ансамбля атомов рубидия к другому ансамблю атомов рубидия на расстояние 150 метров (490 футов), используя запутанные фотоны. В 2016 году исследователи продемонстрировали квантовую телепортацию с двумя независимыми источниками, разделенными 6,5 км (4,0 мили) в оптоволоконной сети Хэфэй. В сентябре 2016 года исследователи из Университета Калгари продемонстрировали квантовую телепортацию по городской оптоволоконной сети Калгари на расстояние 6,2 км (3,9 мили). В декабре 2020 года в рамках сотрудничества INQNET исследователи достигли квантовой телепортации на общее расстояние 44 км (27,3 мили) с точностью, превышающей 90%.

Исследователи также успешно использовали квантовую телепортацию для передачи информации между облаками атомов газа, что примечательно тем, что облака газа представляют собой макроскопические атомные ансамбли.

Также возможно телепортировать логические операции , см. телепортацию с квантовыми воротами . В 2018 году физики из Йельского университета продемонстрировали детерминированную телепортированную операцию CNOT между логически закодированными кубитами.

Схема эксперимента по квантовой телепортации, проведенного группой Цайлингера в 1997 году. Подробности см. в тексте.

Впервые предложенная теоретически в 1993 году, квантовая телепортация с тех пор была продемонстрирована во многих различных формах. Это было осуществлено с использованием двухуровневых состояний одного фотона, одного атома и захваченного иона – среди других квантовых объектов – а также с использованием двух фотонов. В 1997 году две группы экспериментально достигли квантовой телепортации. Первая группа, возглавляемая Санду Попеску , базировалась в Италии. экспериментальная группа под руководством Антона Цайлингера Несколько месяцев спустя за ним последовала .

Результаты, полученные в результате экспериментов, проведенных группой Попеску, пришли к выводу, что сами по себе классические каналы не могут воспроизвести телепортацию линейно поляризованного состояния и эллиптически поляризованного состояния. Измерение состояния Белла различает четыре состояния Белла, которые в идеальном представлении могут обеспечить 100% успешную телепортацию.

Группа Цайлингера создала пару запутанных фотонов, реализовав процесс параметрического преобразования с понижением частоты. Чтобы гарантировать, что два фотона нельзя будет различить по времени их прибытия, фотоны генерировались с использованием импульсного луча накачки. Затем фотоны пропускались через узкополосные фильтры, чтобы обеспечить время когерентности, которое намного превышает длину импульса накачки. Затем они использовали двухфотонную интерферометрию для анализа запутанности, чтобы можно было распознать квантовое свойство при его передаче от одного фотона к другому.

Фотон 1 был поляризован под углом 45° в первом эксперименте, проведенном группой Цайлингера. Квантовая телепортация подтверждается, когда оба фотона обнаруживаются в $|\Psi ^{-}\rangle _{12}$ состояние, вероятность которого составляет 25%. Два детектора f1 и f2 размещаются за светоделителем, и регистрация совпадений позволяет идентифицировать $|\Psi ^{-}\rangle _{12}$ состояние. Если между детекторами f1 и f2 имеется совпадение, то прогнозируется, что фотон 3 будет поляризован под углом 45°. Фотон 3 проходит через поляризационный светоделитель, который выбирает поляризацию +45 ° и -45 °. Если произошла квантовая телепортация, только детектор d2, находящийся на выходе +45°, зарегистрирует обнаружение. Детектор d1, расположенный на выходе −45°, фотон не обнаружит. Если есть совпадение между d2f1f2 с анализом 45 ° и отсутствием совпадения d1f1f2 с анализом -45 °, это является доказательством того, что информация от поляризованного фотона 1 была телепортирована к фотону 3 с использованием квантовой телепортации.

Квантовая телепортация на расстояние 143 км

Группа Цайлингера разработала эксперимент с использованием активной прямой связи в реальном времени и двух оптических каналов в свободном пространстве, квантовой и классической, между Канарскими островами Ла-Пальма и Тенерифе на расстоянии более 143 километров. Результаты были опубликованы в 2012 году. Для достижения телепортации были реализованы частотно-некоррелированный источник пар фотонов, запутанных по поляризации, сверхмалошумящие детекторы одиночных фотонов и тактовая синхронизация с помощью запутывания. Эти две локации были связаны, чтобы разделить вспомогательное состояние:

$|\Psi ^{-}\rangle _{23}={\frac {1}{\surd 2}}((|H\rangle _{2}|V\rangle _{3})-(|V\rangle _{2}|H\rangle _{3}))$

Ла Пальму и Тенерифе можно сравнить с квантовыми персонажами Алисой и Бобом. Алиса и Боб разделяют запутанное состояние, описанное выше: фотон 2 находится у Алисы, а фотон 3 — у Боба. Третья сторона, Чарли, предоставляет фотон 1 (входной фотон), который будет телепортирован Алисе в состоянии обобщенной поляризации:

$|\phi \rangle _{1}=\alpha |H\rangle _{1}+\beta |V\rangle _{1}$

где комплексные числа $\alpha$ и $\beta$ неизвестны Алисе и Бобу.

Алиса выполнит измерение состояния Белла (BSM), которое случайным образом проецирует два фотона на одно из четырех состояний Белла, причем вероятность каждого из них равна 25%. Фотон 3 будет проецироваться на $|\phi \rangle$, состояние входа. Алиса передает результат BSM Бобу по классическому каналу, где Боб может применить соответствующую унитарную операцию для получения фотона 3 в исходном состоянии фотона 1. Бобу не придется ничего делать, если он обнаружит $|\psi ^{-}\rangle _{12}$ состояние. Бобу нужно будет применить $\pi$ фазовый сдвиг фотона 3 между горизонтальной и вертикальной компонентами, если $|\psi ^{+}\rangle _{12}$ состояние обнаружено.

Результаты группы Цайлингера пришли к выводу, что средняя точность (перекрытие идеального телепортированного состояния с измеренной матрицей плотности) составила 0,863 со стандартным отклонением 0,038. Затухание линии связи во время экспериментов варьировалось от 28,1 дБ до 39,0 дБ, что было результатом сильного ветра и резких изменений температуры. Несмотря на высокие потери в квантовом канале свободного пространства, средняя точность превысила классический предел 2/3. Таким образом, группа Цайлингера успешно продемонстрировала квантовую телепортацию на расстояние 143 км.

через реку

В 2004 году был проведен эксперимент по квантовой телепортации через реку Дунай в Вене на расстояние в общей сложности 600 метров. Волоконно-оптический провод длиной 800 метров был проложен в общественной канализационной системе под рекой Дунай и подвергался изменениям температуры и другим воздействиям окружающей среды. Алиса должна выполнить совместное измерение состояния Белла (BSM) для фотона b, входного фотона, и фотона c, ее части запутанной пары фотонов (фотонов c и d). Фотон d, фотон-приемник Боба, будет содержать всю информацию о входном фотоне b, за исключением поворота фазы, который зависит от состояния, которое наблюдала Алиса. В этом эксперименте реализована система активной прямой связи, которая отправляет результаты измерений Алисы по классическому микроволновому каналу с быстрым электрооптическим модулятором, чтобы точно воспроизвести входной фотон Алисы. Точность телепортации, полученная из состояния линейной поляризации при 45 °, варьировалась от 0,84 до 0,90, что значительно превышает классический предел точности 0,66.

атомов

Для этого процесса необходимы три кубита: исходный кубит отправителя, вспомогательный кубит и целевой кубит получателя, который максимально запутан со вспомогательным кубитом. Для этого эксперимента ${\ce {^{40}Ca+}}$ ионы использовались в качестве кубитов. Ионы 2 и 3 получаются в состоянии Белла. $|\psi ^{+}\rangle _{23}={\frac {1}{\sqrt {2}}}(|0\rangle _{2}|1\rangle _{3}+|1\rangle _{2}|0\rangle _{3})$. Состояние иона 1 готовится произвольно. Квантовые состояния ионов 1 и 2 измеряются путем освещения их светом определенной длины волны. Полученная точность для этого эксперимента варьировалась от 73% до 76%. Это больше, чем максимально возможная средняя точность в 66,7%, которую можно получить, используя полностью классические ресурсы.

Квантовая телепортация на Землю-спутник

Квантовое состояние, телепортируемое в этом эксперименте, равно $|\chi \rangle _{1}=\alpha |H\rangle _{1}+\beta |V\rangle _{1}$, где $\alpha$ и $\beta$ неизвестные комплексные числа, $|H\rangle$ представляет состояние горизонтальной поляризации, и $|V\rangle$ представляет состояние вертикальной поляризации. Кубит, приготовленный в таком состоянии, создается в лаборатории в Нгари, Тибет. Целью было телепортировать квантовую информацию кубита на спутник Мициус, запущенный 16 августа 2016 года на высоту около 500 км. Когда измерение состояния Белла проводится на фотонах 1 и 2, и результирующее состояние $|\phi ^{+}\rangle _{12}={\frac {1}{\sqrt {2}}}(|H\rangle _{1}|H\rangle _{2}+|V\rangle _{1}|V\rangle _{2}))$, фотон 3 несет это желаемое состояние. Если обнаружено состояние Bell $|\phi ^{-}\rangle _{12}={\frac {1}{\sqrt {2}}}(|H\rangle _{1}|H\rangle _{2}-|V\rangle _{1}|V\rangle _{2})$, то фазовый сдвиг $\pi$ применяется к состоянию для получения желаемого квантового состояния. Расстояние между наземной станцией и спутником меняется от 500 км до 1400 км. Из-за изменения расстояния потери в канале восходящей линии связи варьируются от 41 дБ до 52 дБ. Средняя точность, полученная в результате этого эксперимента, составила 0,80 со стандартным отклонением 0,01. Таким образом, этот эксперимент успешно установил связь между землей и спутником на расстоянии 500–1400 км с использованием квантовой телепортации. Это важный шаг на пути к созданию квантового Интернета глобального масштаба.

Официальная презентация

Существует множество способов математически записать протокол телепортации. Некоторые из них очень компактны, но абстрактны, а некоторые многословны, но просты и конкретны. Приведенное ниже представление относится к последней форме: многословно, но его преимущество состоит в том, что каждое квантовое состояние показано просто и непосредственно. В последующих разделах рассматриваются более компактные обозначения.

Протокол телепортации начинается с квантового состояния или кубита. $|\psi \rangle$, принадлежащий Алисе, который она хочет передать Бобу. В общем виде этот кубит можно записать в обозначениях Бракетта как:

$|\psi \rangle _{C}=\alpha |0\rangle _{C}+\beta |1\rangle _{C}.$

Индекс C выше используется только для того, чтобы отличить это состояние от A и B ниже.

Далее протокол требует, чтобы Алиса и Боб находились в максимально запутанном состоянии. Это состояние фиксируется заранее по взаимному соглашению между Алисой и Бобом и может быть любым из четырех показанных состояний Белла . Неважно какой.

$|\Phi ^{+}\rangle _{AB}={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}+|1\rangle _{A}\otimes |1\rangle _{B})$,

$|\Psi ^{+}\rangle _{AB}={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |1\rangle _{B}+|1\rangle _{A}\otimes |0\rangle _{B})$,

$|\Psi ^{-}\rangle _{AB}={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B})$.

$|\Phi ^{-}\rangle _{AB}={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}-|1\rangle _{A}\otimes |1\rangle _{B})$,

Далее предположим, что Алиса и Боб разделяют состояние. $|\Phi ^{+}\rangle _{AB}.$Алиса получает одну из частиц пары, а другая достается Бобу. (Это реализуется путем подготовки частиц вместе и отправки их Алисе и Бобу из общего источника.) Индексы A и B в запутанном состоянии относятся к частице Алисы или Боба.

На данный момент у Алисы есть две частицы ( C та, которую она хочет телепортировать, и A — одна из запутанной пары), а у Боба — одна частица, B. — В полной системе состояние этих трех частиц определяется выражением

$|\psi \rangle _{C}\otimes |\Phi ^{+}\rangle _{AB}=(\alpha |0\rangle _{C}+\beta |1\rangle _{C})\otimes {\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}+|1\rangle _{A}\otimes |1\rangle _{B}).$

Затем Алиса проведет локальное измерение в базисе Белла (т.е. четырех состояниях Белла) для двух частиц, находящихся в ее распоряжении. Чтобы результат измерения был понятен, лучше всего записать состояние двух кубитов Алисы в виде суперпозиции базиса Белла. Это делается с помощью следующих общих тождеств, которые легко проверяются:

$|0\rangle \otimes |0\rangle ={\frac {1}{\sqrt {2}}}(|\Phi ^{+}\rangle +|\Phi ^{-}\rangle ),$

$|0\rangle \otimes |1\rangle ={\frac {1}{\sqrt {2}}}(|\Psi ^{+}\rangle +|\Psi ^{-}\rangle ),$

$|1\rangle \otimes |0\rangle ={\frac {1}{\sqrt {2}}}(|\Psi ^{+}\rangle -|\Psi ^{-}\rangle ),$

и

$|1\rangle \otimes |1\rangle ={\frac {1}{\sqrt {2}}}(|\Phi ^{+}\rangle -|\Phi ^{-}\rangle ).$

После расширения выражения для ${\textstyle {\begin{aligned}|&\psi \rangle _{C}\otimes \ |\Phi ^{+}\rangle _{AB}\end{aligned}}}$, эти тождества применяются к кубитам с A и C. индексами В частности,

$$\alpha {\frac {1}{\sqrt {2}}}|0\rangle _{C}\otimes |0\rangle _{A}\otimes |0\rangle _{B}=\alpha {\frac {1}{2}}(|\Phi ^{+}\rangle _{CA}+|\Phi ^{-}\rangle _{CA})\otimes |0\rangle _{B},$$

и остальные термины следуют аналогично. Объединив подобные термины, общее трехчастичное состояние A , B и C вместе становится следующей четырехчленной суперпозицией:

${\begin{aligned}|&\psi \rangle _{C}\otimes \ |\Phi ^{+}\rangle _{AB}\ =\\{\frac {1}{2}}{\Big \lbrack }\ &|\Phi ^{+}\rangle _{CA}\otimes (\alpha |0\rangle _{B}+\beta |1\rangle _{B})\ +\ |\Phi ^{-}\rangle _{CA}\otimes (\alpha |0\rangle _{B}-\beta |1\rangle _{B})\\\ +\ &|\Psi ^{+}\rangle _{CA}\otimes (\alpha |1\rangle _{B}+\beta |0\rangle _{B})\ +\ |\Psi ^{-}\rangle _{CA}\otimes (\alpha |1\rangle _{B}-\beta |0\rangle _{B}){\Big \rbrack }.\\\end{aligned}}$

Обратите внимание, что все три частицы все еще находятся в одном и том же состоянии, поскольку никаких операций не выполнялось. Скорее всего, вышеизложенное — это просто изменение основы в части системы Алисы. Это изменение переместило запутанность от частиц A и B к частицам C и A. Фактическая телепортация происходит, когда Алиса измеряет свои два кубита (C и A) в базисе Белла.

Простая квантовая схема, которая отображает одно из четырех состояний Белла (пара ЭПР на картинке) в одно из четырех двухкубитных состояний вычислительного базиса. Схема состоит из вентиля CNOT, за которым следует операция Адамара . В выходных данных a и b принимают значения 0 или 1.

$|\Phi ^{+}\rangle _{CA},|\Phi ^{-}\rangle _{CA},|\Psi ^{+}\rangle _{CA},|\Psi ^{-}\rangle _{CA}.$

Эквивалентно, измерение может быть выполнено на вычислительной основе, $\{|0\rangle ,|1\rangle \}$, однозначно отображая каждое состояние Белла в одно из $\{|0\rangle \otimes |0\rangle ,|0\rangle \otimes |1\rangle ,|1\rangle \otimes |0\rangle ,|1\rangle \otimes |1\rangle \}$ с квантовой схемой на рисунке справа.

трехчастичного состояния. Результатом (локального) измерения Алисы является набор двух классических битов (00, 01, 10 или 11), относящихся к одному из следующих четырех состояний (с равной вероятностью 1/4), после коллапса в одно из состояний:

• $|\Phi ^{+}\rangle _{CA}\otimes (\alpha |0\rangle _{B}+\beta |1\rangle _{B})$
• $|\Phi ^{-}\rangle _{CA}\otimes (\alpha |0\rangle _{B}-\beta |1\rangle _{B})$
• $|\Psi ^{+}\rangle _{CA}\otimes (\alpha |1\rangle _{B}+\beta |0\rangle _{B})$
• $|\Psi ^{-}\rangle _{CA}\otimes (\alpha |1\rangle _{B}-\beta |0\rangle _{B})$

Две частицы Алисы теперь запутаны друг с другом в одном из четырех состояний Белла , и запутанность, первоначально разделявшаяся между частицами Алисы и Боба, теперь нарушена. Частица Боба принимает одно из четырех состояний суперпозиции, показанных выше. Обратите внимание, что кубит Боба теперь находится в состоянии, напоминающем состояние телепортации. Четыре возможных состояния кубита Боба представляют собой унитарные образы состояния, которое необходимо телепортировать.

Результат измерения Белла Алисы сообщает ей, в каком из четырех вышеперечисленных состояний находится система. Теперь она может отправить свой результат Бобу по классическому каналу. Два классических бита могут сообщить, какой из четырех результатов она получила. После того, как Боб получит сообщение от Алисы, он узнает, в каком из четырех состояний находится его частица. Используя эту информацию, он выполняет над своей частицей унитарную операцию по преобразованию ее в желаемое состояние. $\alpha |0\rangle _{B}+\beta |1\rangle _{B}$:

• Если Алиса указывает, что ее результат $|\Phi ^{+}\rangle _{CA}$Боб знает, что его кубит уже находится в желаемом состоянии, и ничего не делает. Это соответствует тривиальной унитарной операции — тождественному оператору.
• Если в сообщении указано $|\Phi ^{-}\rangle _{CA}$Боб отправит свой кубит через унитарный квантовый вентиль, заданный матрицей Паули.

$\sigma _{3}={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}$

восстановить государство.

• Если сообщение Алисы соответствует $|\Psi ^{+}\rangle _{CA}$, Боб применяет ворота

$\sigma _{1}={\begin{bmatrix}0&1\\1&0\end{bmatrix}}$

своему кубиту.

• Наконец, для оставшегося случая соответствующий вентиль определяется выражением

$\sigma _{3}\sigma _{1}=-\sigma _{1}\sigma _{3}=i\sigma _{2}={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}.$

Таким образом достигается телепортация. Упомянутые выше три вентиля соответствуют поворотам на π радиан (180°) вокруг соответствующих осей (X, Y и Z) в изображении сферы Блоха кубита.

Некоторые замечания:

• После этой операции кубит Боба примет состояние $|\psi \rangle _{B}=\alpha |0\rangle _{B}+\beta |1\rangle _{B}$, и кубит Алисы становится (неопределённой) частью запутанного состояния. Телепортация не приводит к копированию кубитов и, следовательно, согласуется с теоремой о запрете клонирования .
• Здесь не происходит никакой передачи материи или энергии. Частица Алисы не была физически перемещена к Бобу; было передано только его состояние. Термин «телепортация», придуманный Беннеттом, Брассаром, Крепо, Жожой, Пересом и Вуттерсом, отражает неразличимость квантово-механических частиц.
• Для каждого телепортированного кубита Алисе необходимо отправить Бобу два классических бита информации. Эти два классических бита не несут полной информации о телепортируемом кубите. Если перехватчик перехватит эти два бита, он может точно знать, что Бобу нужно сделать, чтобы восстановить желаемое состояние. Однако эта информация бесполезна, если она не сможет взаимодействовать с запутанной частицей, находящейся в распоряжении Боба.

квантовой

При реализации протокола квантовой телепортации могут возникнуть различные экспериментальные шумы, влияющие на перенос состояний. . Обычный способ оценить конкретную процедуру телепортации — использовать среднюю точность : Учитывая произвольный протокол телепортации, создающий выходные состояния. $\rho _{i}$ с вероятностью $p_{i}$ для начального состояния $\rho =|\psi \rangle \langle \psi |$, средняя точность определяется как :

$\langle {\overline {F}}\rangle =\int \sum _{i}p_{i}F(\rho ,\rho _{i})d\psi$

где интегрирование осуществляется по мере Хаара , определяемой в предположении максимальной неопределенности относительно начальных квантовых состояний. $|\psi \rangle$, и $F(\rho ,\rho _{i})=\left({\text{Tr}}{\sqrt {{\sqrt {\rho }}\rho _{i}{\sqrt {\rho }}}}\right)^{2}$ Ульмана-Йожы – это верность .

Широко известный классический порог получается путем оптимизации средней точности по всем классическим протоколам (т.е. когда отправитель Алиса и получатель Боб могут использовать только классический канал для связи друг с другом). Когда телепортация включает состояния кубита, максимальная классическая средняя точность равна $2/3$. Таким образом, конкретный протокол со средней точностью $\langle {\overline {F}}\rangle$ считается полезным , если $\langle {\overline {F}}\rangle \geq 2/3$.

Ульмана-Йожсы Однако использование точности в качестве уникальной меры расстояния для сравнительного анализа телепортации не оправдано, и можно выбрать другие меры различимости. . Например, в зависимости от контекста могут существовать причины, в которых другие меры могут быть более подходящими, чем верность. . Таким образом, среднее расстояние телепортации определяется как :

$\langle {\overline {D}}\rangle =\int \sum _{i}p_{i}D(\rho ,\rho _{i})d\psi$

существование $D(\rho ,\sigma )$ корректная (т.е. удовлетворяющая идентичности неразличимых величин и унитарной инвариантности) мера различимости между квантовыми состояниями. Следовательно, существуют разные классические пороги в зависимости от рассматриваемой меры расстояния (классические пороги для расстояния Следа , квантовой расходимости Дженсена-Шеннона , расстояния передачи, расстояния Буреса , расстояния Вуттерса и квантового расстояния Хеллингера, среди других, были получены в работе [12]. ). Это указывает на особую проблему при сертификации квантовой телепортации: учитывая протокол телепортации, его сертификация не является универсальным фактом в том смысле, что он зависит от используемого расстояния. Затем конкретный протокол может быть сертифицирован как полезный для набора кванторов расстояния и бесполезный для других мер различимости. .

Альтернативные обозначения

Квантовая телепортация в ее схематической форме. используя графическую нотацию Пенроуза . Формально такое вычисление происходит в категории кинжального компакта . Это приводит к абстрактному описанию квантовой телепортации, используемому в категориальной квантовой механике .

Представление квантовой схемы для телепортации квантового состояния, как описано выше . Схема потребляет $|\Phi ^{+}\rangle$ Состояние Белла и кубит для телепортации в качестве входных данных и состоит из CNOT , Адамара , двух измерений двух кубитов и, наконец, двух вентилей с классическим управлением : Паули X и Паули Z , что означает, что если результат измерения был $|1\rangle$, то выполняется классически управляемый вентиль Паули. После завершения работы схемы значение $|\psi \rangle _{C}$ переместится или телепортируется туда $|\psi \rangle _{B}$, и $|\psi \rangle _{C}$ будет иметь значение либо $|0\rangle$ или $|1\rangle$, в зависимости от результата измерения этого кубита.
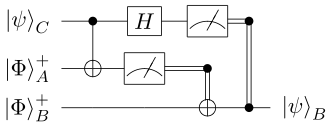
Эту схему также можно использовать для замены запутанности , если $|\psi \rangle _{C}$ — один из кубитов, составляющих запутанное состояние, как описано в тексте .

Существует множество различных обозначений, описывающих протокол телепортации. Одним из распространенных является использование обозначения квантовых вентилей .

В приведенном выше выводе унитарное преобразование, представляющее собой замену базиса (из стандартного базиса произведения в базис Белла), может быть записано с использованием квантовых вентилей. Непосредственный расчет показывает, что этот элемент определяется выражением

$G=(H\otimes I)\operatorname {CNOT}$

где H — однокубитный вентиль Уолша-Адамара и $\operatorname {CNOT}$ — это ворота «Управляемое НЕ».

Обмен запутанностью

Телепортацию можно применять не только к чистым состояниям, но и к смешанным состояниям , которые можно рассматривать как состояние отдельной подсистемы запутанной пары. Так называемая замена запутанности — простой и наглядный пример.

Если у Алисы и Боба запутанная пара, и Боб телепортирует свою частицу Кэрол, то частица Алисы теперь запутана с частицей Кэрол. Эту ситуацию можно также рассматривать симметрично следующим образом:

У Алисы и Боба одна запутанная пара, а у Боба и Кэрол — другая запутанная пара. Теперь позвольте Бобу выполнить проективное измерение двух своих частиц в базисе Белла и сообщить результат Кэрол. Эти действия в точности соответствуют протоколу телепортации, описанному выше, где первая частица Боба, запутанная с частицей Алисы, является состоянием, подлежащим телепортации. Когда Кэрол заканчивает протокол, у нее теперь есть частица в телепортированном состоянии, то есть в запутанном состоянии с частицей Алисы. Таким образом, хотя Алиса и Кэрол никогда не взаимодействовали друг с другом, их частицы теперь запутаны.

Подробный схематический вывод замены запутанности был дан Бобом Коке . представлено в терминах категориальной квантовой механики .

Алгоритм замены пар Белла

Важным применением обмена запутанностью является распределение состояний Белла для использования в распределенных квантовых сетях запутанности . Техническое описание протокола замены запутанности приведено здесь для чистых состояний Белла.

1. Алиса и Боб локально подготавливают известные пары Белла, в результате чего получается начальное состояние:
   $|\psi \rangle _{\rm {in}}=|\Phi ^{+}\rangle _{A_{1},A_{2}}|\Phi ^{+}\rangle _{B_{1},B_{2}}$
2. Алиса отправляет кубит $A_{1}$ третьему лицу Кэрол
3. Боб отправляет кубит $B_{1}$ Кэрол
4. Кэрол выполняет проекцию Белла между $A_{1}$ и $B_{1}$ это случайно (все четыре состояния Белла возможны и распознаваемы) приводит к результату измерения:
   $\langle \Phi ^{+}|_{A_{1},B_{1}}|\psi \rangle _{\rm {in}}=|\Phi ^{+}\rangle _{A_{2},B_{2}}$
5. В случае трех других результатов проекции Белла локальные поправки, вносимые операторами Паули, вносятся Алисой и/или Бобом после того, как Кэрол сообщила результаты измерения.
   $\langle \Phi ^{-}|_{A_{1},B_{1}}|\psi \rangle _{\rm {in}}={\hat {Z}}_{B_{2}}|\Phi ^{+}\rangle _{A_{2},B_{2}}$
   $\langle \Psi ^{+}|_{A_{1},B_{1}}|\psi \rangle _{\rm {in}}={\hat {X}}_{B_{2}}|\Phi ^{+}\rangle _{A_{2},B_{2}}$
   $\langle \Psi ^{-}|_{A_{1},B_{1}}|\psi \rangle _{\rm {in}}={\hat {X}}_{B_{2}}{\hat {Z}}_{B_{2}}|\Phi ^{+}\rangle _{A_{2},B_{2}}$
6. У Алисы и Боба теперь есть пара Белла между кубитами. $A_{2}$ и $B_{2}$
   $|\psi \rangle _{\rm {out}}=|\Phi ^{+}\rangle _{A_{2},B_{2}}$

Обобщения протокола телепортации

Описанный выше базовый протокол телепортации кубита был обобщен в нескольких направлениях, в частности, в отношении размера телепортируемой системы и количества участвующих сторон (отправителя, контроллера или получателя).

d -мерные системы

Обобщение $d$Системы многоуровневого уровня (так называемые кудиты ) просты и уже обсуждались в оригинальной статье Беннетта и др. : максимально запутанное состояние двух кубитов должно быть заменено максимально запутанным состоянием двух кудитов, а измерение Белла - измерением, определяемым максимально запутанным ортонормированным базисом. Все возможные такие обобщения обсуждались Вернером в 2001 году.

Обобщение на бесконечномерные так называемые системы с непрерывными переменными было предложено Браунштейном и Кимблом. и привело к первому эксперименту по телепортации, который сработал безоговорочно.

Многосторонние версии

Использование многочастных запутанных состояний вместо двухчастного максимально запутанного состояния обеспечивает несколько новых функций: либо отправитель может телепортировать информацию нескольким получателям, либо отправлять одно и то же состояние всем из них (что позволяет уменьшить количество запутанности, необходимое для процесса). ) или телепортация многосторонних состояний или отправку в одно государство таким образом, что принимающим сторонам необходимо сотрудничать для извлечения информации. Другой способ рассмотрения последней настройки заключается в том, что некоторые стороны могут контролировать, могут ли другие телепортироваться.

Телепортация логических ворот

Основная статья: Телепортация с помощью квантовых ворот

В общем, смешанные состояния можно переносить ρ, а во время телепортации применять линейное преобразование ω, что позволяет обрабатывать данные квантовой информации. Это один из основополагающих строительных блоков квантовой обработки информации. Это продемонстрировано ниже.

Общее описание

Общую схему телепортации можно описать следующим образом. Задействованы три квантовые системы. Система 1 — это (неизвестное) состояние ρ, которое Алиса должна телепортировать. Системы 2 и 3 находятся в максимально запутанном состоянии ω, которое распространяется на Алису и Боба соответственно. Тогда вся система находится в состоянии

$\rho \otimes \omega .$

Успешный процесс телепортации — это LOCC квантовый канал Φ, который удовлетворяет условию

$(\operatorname {Tr} _{12}\circ \Phi )(\rho \otimes \omega )=\rho \,,$

где Tr ₁₂ — операция частичного следа по системам 1 и 2, а $\circ$ обозначает состав карт. Это описывает канал на картинке Шрёдингера.

Учитывая сопряженные отображения в картине Гейзенберга, условие успеха становится

$\langle \Phi (\rho \otimes \omega )|I\otimes O\rangle =\langle \rho |O\rangle$

для всех наблюдаемых O в системе Боба. Тензорный коэффициент в $I\otimes O$ является $12\otimes 3$ в то время как $\rho \otimes \omega$ является $1\otimes 23$.

Подробности

Предлагаемый канал Φ можно описать более подробно. Чтобы начать телепортацию, Алиса выполняет локальное измерение двух имеющихся у нее подсистем (1 и 2). Предположим, что локальные измерения имеют эффекты

${F_{i}}={M_{i}^{2}}.$

Если измерение регистрирует i -й результат, общее состояние рушится до

$(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I).$

Тензорный коэффициент в $(M_{i}\otimes I)$ является $12\otimes 3$ в то время как $\rho \otimes \omega$ является $1\otimes 23$. Затем Боб применяет соответствующую локальную операцию Ψ _i к системе 3. В комбинированной системе это описывается формулой

$(Id\otimes \Psi _{i})(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I).$

где Id — карта идентичности составной системы. $1\otimes 2$.

Следовательно, канал Φ определяется формулой

$\Phi (\rho \otimes \omega )=\sum _{i}(Id\otimes \Psi _{i})(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I)$

Обратите внимание: Φ удовлетворяет определению LOCC . Как указано выше, телепортация считается успешной, если для всех наблюдаемых O в системе Боба выполняется равенство

$\langle \Phi (\rho \otimes \omega ),I\otimes O\rangle =\langle \rho ,O\rangle$

держит. Левая часть уравнения:

$\sum _{i}\langle (Id\otimes \Psi _{i})(M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I),\;I\otimes O\rangle$

$=\sum _{i}\langle (M_{i}\otimes I)(\rho \otimes \omega )(M_{i}\otimes I),\;I\otimes \Psi _{i}^{*}(O)\rangle$

где Ψ _i * — сопряженный к Ψ _i в картине Гейзенберга. Предполагая, что все объекты конечномерны, это становится

$\sum _{i}\operatorname {Tr} \;(\rho \otimes \omega )(F_{i}\otimes \Psi _{i}^{*}(O)).$

Критерий успеха телепортации имеет выражение

$\sum _{i}\operatorname {Tr} \;(\rho \otimes \omega )(F_{i}\otimes \Psi _{i}^{*}(O))=\operatorname {Tr} \;\rho \cdot O.$

Местное объяснение явления

Локальное объяснение квантовой телепортации предложено Дэвидом Дойчем и Патриком Хейденом в отношении многомировой интерпретации квантовой механики. В их статье утверждается, что два бита, которые Алиса отправляет Бобу, содержат «локально недоступную информацию», что приводит к телепортации квантового состояния. «Способность квантовой информации течь по классическому каналу [...], сохраняя декогерентность, является [...] основой квантовой телепортации».

Последние события

Хотя квантовая телепортация находится на зачаточном этапе, существует множество аспектов телепортации, над которыми ученые работают, чтобы лучше понять или улучшить этот процесс, в том числе:

Высшие измерения

Квантовая телепортация может уменьшить количество ошибок, связанных с отказоустойчивыми квантовыми вычислениями, за счет расположения логических элементов. Эксперименты Д. Готтесмана и И. Л. Чуанга установили, что существует «иерархия Клиффорда». расположение ворот, которое усиливает защиту от экологических ошибок. В целом, в иерархии Клиффорда допускается более высокий порог ошибки, поскольку последовательность элементов требует меньше ресурсов, необходимых для вычислений. В то время как большее количество вентилей, используемых в квантовом компьютере, создает больше шума, расположение вентилей и использование телепортации при передаче логики могут уменьшить этот шум, поскольку это требует меньшего «трафика», который компилируется в этих квантовых сетях. Чем больше кубитов используется в квантовом компьютере, тем больше уровней добавляется к расположению вентилей, причем степень диагонализации расположения вентилей варьируется. Анализ более высокого измерения включает в себя расположение ворот более высокого уровня иерархии Клиффорда.

Качество информации

Учитывая ранее упомянутое требование наличия промежуточного запутанного состояния для квантовой телепортации, необходимо учитывать чистоту этого состояния для качества информации. Разработанная защита предполагает использование непрерывной переменной информации (а не типичной дискретной переменной), создавая наложенное когерентное промежуточное состояние. Это включает в себя фазовый сдвиг полученной информации, а затем добавление этапа смешивания после приема с использованием предпочтительного состояния, которое может быть нечетным или четным когерентным состоянием, которое будет «обусловлено классической информацией отправителя», создавая двухрежимный режим. состояние, содержащее первоначально отправленную информацию.

Также были разработки по телепортации информации между системами, в которых уже есть квантовая информация. Эксперименты, проведенные Фэном, Сюй, Чжоу и др. продемонстрировали, что телепортация кубита к фотону, который уже имеет кубитную информацию, возможна благодаря использованию оптического затвора, связывающего кубит-кварт. Это качество может увеличить возможности вычислений, поскольку расчеты могут выполняться на основе ранее сохраненной информации, что позволяет улучшить прошлые расчеты.

См. также

• Сверхплотное кодирование
• Квантовая комплексная сеть
• Квантовая механика
  • Введение в квантовую механику
  • Квантовый компьютер
  • Квантовая криптография
  • Квантовая нелокальность
  • Принцип неопределенности Гейзенберга
• Теория поглотителя Уиллера – Фейнмана

Ссылки

Общие

• Обзор по теории и экспериментам:
  • Пирандола, С.; Эйсерт, Дж.; Уидбрук, К.; Фурусава, А.; Браунштейн, С.Л. (2015). «Достижения в области квантовой телепортации». Природная фотоника . 9 (10): 641–652. arXiv : 1505.07831 . Бибкод : 2015NaPho...9..641P . дои : 10.1038/nphoton.2015.154 . S2CID   15074330 .
• Теоретическое предложение:
  • Беннетт, Чарльз Х.; Брассар, Жиль ; Крепо, Клод; Джожа, Ричард; Перес, Ашер; Вуттерс, Уильям К. (29 марта 1993 г.). «Телепортация неизвестного квантового состояния через двойные классические каналы и каналы Эйнштейна – Подольского – Розена». Физ. Преподобный Летт . 70 (13): 1895–1899. Бибкод : 1993PhRvL..70.1895B . doi : 10.1103/PhysRevLett.70.1895 . ПМИД   10053414 . S2CID   6599630 . Это основополагающий документ, в котором изложен протокол запутанности.
  • Вайдман, Л. (февраль 1994 г.). «Телепортация квантовых состояний». Физ. Преподобный А. 49 (2): 1473–1476. arXiv : hep-th/9305062 . Бибкод : 1994PhRvA..49.1473V . дои : 10.1103/physreva.49.1473 . ПМИД   9910380 . S2CID   8356637 .
  • Шахриар, М.С.; Прадхан, П.; Гопал, В.; Морзински Дж.; Кардозо, Дж.; Пати, GS (2006). «Фиксация длины волны посредством телепортации с использованием удаленной квантовой запутанности и колебаний Блоха – Зигерта». Оптические коммуникации . 266 (1): 349–353. Бибкод : 2006OptCo.266..349S . дои : 10.1016/j.optcom.2006.04.072 .
  • Брассар, Дж .; Браунштейн, С ; Клив, Р. (1998). «Телепортация как квантовое вычисление». Физика Д. 120 (1–2): 43–47. arXiv : Quant-ph/9605035 . Бибкод : 1998PhyD..120...43B . дои : 10.1016/s0167-2789(98)00043-8 . S2CID   15178313 .
  • Перес, Ашер (2003). «Что на самом деле телепортируется?». arXiv : Quant-ph/0304158 .
  • Риголин, Густаво (2005). «Квантовая телепортация произвольного двухкубитного состояния и ее связь с многочастной запутанностью». Физический обзор А. 71 (3): 032303. arXiv : quant-ph/0407219 . Бибкод : 2005PhRvA..71c2303R . дои : 10.1103/PhysRevA.71.032303 . S2CID   53941971 .
  • Ши-Бяо Чжэн (2004) «Схема приближенной условной телепортации неизвестного атомного состояния без измерения состояния Белла», Phys. Ред. А 69 , 064302
  • Кардозо, Уэсли Б.; Авелар, АТ; Басея, Б.; Де Алмейда, Н.Г. (2005). «Телепортация запутанных состояний без измерения состояния Белла». Физический обзор А. 72 (4). 045802. arXiv : quant-ph/0604156 . Бибкод : 2005PhRvA..72d5802C . дои : 10.1103/PhysRevA.72.045802 . S2CID   11270460 .
  • Лойенбергер, Майкл Н.; Флатте, Майкл Э.; Авшалом, Д.Д. (2005). «Телепортация электронных многокубитных состояний, закодированных в электронном спине квантовых точек, через одиночные фотоны». Письма о физических отзывах . 94 (10). 107401. Бибкод : 2005PhRvL..94j7401L . doi : 10.1103/PhysRevLett.94.107401 . ПМИД   15783519 . S2CID   26932056 .
  • Пырков Алексей Н.; Бирнс, Тим (2014). «Квантовая телепортация спин-когерентных состояний: телепортация за пределами непрерывных переменных». Новый журнал физики . 16 (7). 073038.arXiv ​ : 1305.2479 . Бибкод : 2014NJPh...16g3038P . дои : 10.1088/1367-2630/16/7/073038 . S2CID   118699151 .
  • Вэй, Юйчуань (2016). «Комментарий к «Дробной квантовой механике» и «Дробному уравнению Шредингера» ». Физический обзор E . 93 (6). 066103.arXiv ​ : 1607.01356 . Бибкод : 2016PhRvE..93f6103W . дои : 10.1103/PhysRevE.93.066103 . ПМИД   27415397 . S2CID   20010251 .
• Первые эксперименты с фотонами:
  • Баумистер и др. 1997 г.
  • Бош и др. 1998 год
  • Ким, Ю.-Х.; Кулик, ИП; Ши, Ю. (2001). «Квантовая телепортация состояния поляризации с полным измерением состояния колокола». Физ. Преподобный Летт . 86 (7): 1370–1373. arXiv : Quant-ph/0010046 . Бибкод : 2001PhRvL..86.1370K . дои : 10.1103/PhysRevLett.86.1370 . ПМИД   11178086 . S2CID   6123495 .
  • Марсикич И.; Титтель, В.; Збинден, Х.; Гисин, Н. (2003). «Телепортация кубитов на большие расстояния на телекоммуникационных длинах волн». Природа . 421 (6922): 509–513. arXiv : Quant-ph/0301178 . Бибкод : 2003Natur.421..509M . дои : 10.1038/nature01376 . PMID   12556886 . S2CID   4303767 .
  • Урсин, Руперт; Дженневейн, Томас; Аспельмейер, Маркус; Кальтенбек, Райнер; Линденталь, Майкл; Вальтер, Филип; Цайлингер, Антон (август 2004 г.). «Квантовая телепортационная связь через Дунай» . Природа . 430 (7002): 849. Бибкод : 2004Nature.430..849U . дои : 10.1038/430849а . ПМИД   15318210 . S2CID   4426035 .
• Первые эксперименты с атомами:
  • Рибе, М.; Хеффнер, Х.; Роос, CF; Гензель, В.; Рут, М.; Бенхельм, Дж.; Ланкастер, GPT; Кёрбер, ТВ; Бехер, К.; Шмидт-Калер, Ф.; Джеймс, DFV; Блатт, Р. (2004). «Детерминированная квантовая телепортация с атомами». Природа . 429 (6993): 734–737. Бибкод : 2004Natur.429..734R . дои : 10.1038/nature02570 . ПМИД   15201903 . S2CID   4397716 .
  • Барретт, доктор медицины; Кьяверини, Дж.; Шаец, Т.; Бриттон, Дж.; Итано, ВМ; Йост, доктор медицинских наук; Нилл, Э.; Лангер, К.; Лейбфрид, Д.; Озери, Р.; Вайнленд, диджей (2004). «Детерминированная квантовая телепортация атомных кубитов». Природа . 429 (6993): 737–739. Бибкод : 2004Natur.429..737B . дои : 10.1038/nature02608 . ПМИД   15201904 . S2CID   1608775 .
  • Ольмшенк, С.; Мацукевич, Д.Н.; Маунц, П.; Хейс, Д.; Дуань, Л.-М.; Монро, К. (2009). «Квантовая телепортация между кубитами удаленной материи». Наука . 323 (5913): 486–489. arXiv : 0907.5240 . Бибкод : 2009Sci...323..486O . дои : 10.1126/science.1167209 . ПМИД   19164744 . S2CID   206516918 .

Внешние ссылки

• Тест Белла без лазеек – Институт нанонауки Кавли
• «Жуткое действие и не только» – интервью с Антоном Цайлингером о квантовой телепортации. Дата: 16 февраля 2006 г.
• Квантовая телепортация в IBM. Архивировано 7 января 2011 года в Wayback Machine.
• Физикам удалось передать информацию между материей и светом
• Квантовое телеклонирование: клон капитана Кирка и подслушиватель
• «Подходы к универсальным квантовым вычислениям, основанные на телепортации» . Архивировано из оригинала 18 декабря 2008 г.
• Рибе, М; Чвалла, М; Бенхельм, Дж; Хэффнер, Х; Гензель, В; Роос, CF; Блатт, Р. (4 июля 2007 г.). «Квантовая телепортация атомов: томография квантовых процессов». Новый журнал физики . 9 (7): 211. arXiv : 0704.2027 . Бибкод : 2007NJPh....9..211R . дои : 10.1088/1367-2630/07.09.211 .
• Запутанная государственная телепортация
• О, Сангчул; Ли, Сунчил; Ли, Хай Ун (27 августа 2002 г.). «Верность квантовой телепортации по зашумленным каналам». Физический обзор А. 66 (2): 022316. arXiv : quant-ph/0206173 . Бибкод : 2002PhRvA..66b2316O . дои : 10.1103/PhysRevA.66.022316 . HDL : 10203/1029 .
• TelePOVM - обобщенная схема квантовой телепортации.
• Телепортация запутанности через штаты Вернера
• Квантовая телепортация состояния поляризации
• Чилдресс, Дэвид Хэтчер (1999). Справочник по путешествиям во времени: Руководство по практической телепортации и путешествиям во времени . Приключения без ограничений Press. ISBN  978-0-932813-68-8 .
• Рибе, М.; Хеффнер, Х.; Роос, CF; Гензель, В.; Бенхельм, Дж.; Ланкастер, GPT; Кёрбер, ТВ; Бехер, К.; Шмидт-Калер, Ф.; Джеймс, DFV; Блатт, Р. (июнь 2004 г.). «Детерминированная квантовая телепортация атомов». Природа . 429 (6993): 734–737. Бибкод : 2004Natur.429..734R . дои : 10.1038/nature02570 . ПМИД   15201903 .
• Ким, Юн Хо; Кулик, Сергей; Ши, Яньхуа (январь 2002 г.). «Квантовая телепортация с полным измерением состояния Белла». Журнал современной оптики . 49 (1–2): 221–236. arXiv : Quant-ph/0010046 . Бибкод : 2002JMOp...49..221K . дои : 10.1080/09500340110087633 .
• «Добро пожаловать в квантовый Интернет» . Новости науки . 16 августа 2008 г. Архивировано из оригинала 30 ноября 2012 г. Проверено 14 августа 2008 г.
• Квантовые эксперименты – интерактивные.
• (В основном серьезное) введение в квантовую телепортацию для нефизиков.