Энергия нулевой точки

Похожие статьи см. в разделе «Квантовый вакуум (значения)» .

Не путать с нулевой точкой (фотометрией) .

Чтобы узнать о других значениях, см. Нулевая точка (значения) .

Жидкий гелий сохраняет кинетическую энергию и не замерзает независимо от температуры при стандартном атмосферном давлении благодаря энергии нулевой точки. При охлаждении ниже своей лямбда-точки он проявляет свойства сверхтекучести .

Энергия нулевой точки ( ZPE ) — это минимально возможная энергия , которую квантовомеханическая может иметь система. В отличие от классической механики , квантовые системы постоянно колеблются в своем самом низком энергетическом состоянии, как это описано принципом неопределенности Гейзенберга . Следовательно, даже при абсолютном нуле атомы и молекулы сохраняют некоторое колебательное движение. Помимо атомов и молекул , этими свойствами обладает и пустое пространство вакуума . Согласно квантовой теории поля , Вселенную можно рассматривать не как изолированные частицы, а как непрерывные флуктуирующие поля : поля материи , кванты которых являются фермионами (т. е. лептонами и кварками ), и силовые поля , квантами которых являются бозоны (например, фотоны и глюоны). ). Все эти поля имеют нулевую энергию. Эти флуктуирующие поля нулевой точки приводят к своего рода повторному введению эфира в физику. поскольку некоторые системы могут обнаружить существование этой энергии. Однако этот эфир нельзя рассматривать как физическую среду, если он должен быть лоренц-инвариантным и не противоречить Эйнштейна специальной теории относительности .

Понятие энергии нулевой точки также важно для космологии , и в физике в настоящее время отсутствует полная теоретическая модель для понимания энергии нулевой точки в этом контексте; в частности, несоответствие между теоретической и наблюдаемой энергией вакуума во Вселенной является источником серьезных разногласий. Тем не менее, согласно общей теории относительности Эйнштейна , любая такая энергия будет гравитационно, а экспериментальные данные расширения Вселенной , темной энергии и эффекта Казимира показывают, что любая такая энергия исключительно слаба. Одно из предложений, которое пытается решить эту проблему, состоит в том, чтобы сказать, что поле фермионов имеет отрицательную нулевую энергию, в то время как поле бозонов имеет положительную нулевую энергию, и, таким образом, эти энергии каким-то образом компенсируют друг друга. Эта идея была бы верной, если бы суперсимметрия была точной симметрией природы ; однако БАК в ЦЕРН до сих пор не нашел никаких доказательств, подтверждающих это. Более того, известно, что если суперсимметрия вообще действительна, то это в лучшем случае нарушенная симметрия , верная только при очень высоких энергиях, и никто не смог показать теорию, в которой в низкоэнергетической Вселенной происходят сокращения нулевой точки. мы наблюдаем сегодня. Это несоответствие известно как проблема космологической постоянной и является одной из величайших неразгаданных загадок физики . Многие физики считают, что «вакуум является ключом к полному пониманию природы».

Этимология и терминология

Термин энергия нулевой точки (ZPE) является переводом немецкого Nullpunktsenergie . Иногда взаимозаменяемо с ним используются термины «излучение нулевой точки» и «энергия основного состояния» . Термин «поле нулевой точки» ( ZPF ) можно использовать применительно к конкретному вакуумному полю, например, к вакууму КЭД , который конкретно занимается квантовой электродинамикой с квантовой электродинамикой (например, электромагнитными взаимодействиями между фотонами, электронами и вакуумом). (например, электромагнитным взаимодействием между фотонами, электронами и вакуумом), или к вакууму КХД , который имеет дело с квантовой хромодинамикой (например, взаимодействием цветовых зарядов между кварками, глюонами и вакуумом). Вакуум можно рассматривать не как пустое пространство, а как комбинацию всех полей нулевой точки. В квантовой теории поля эта комбинация полей называется вакуумным состоянием, связанная с ней энергия нулевой точки называется энергией вакуума , а среднее значение энергии называется вакуумным математическим ожиданием (VEV), также называемым его конденсатом .

Обзор

Кинетическая энергия в зависимости от температуры

В классической механике все частицы можно рассматривать как обладающие некоторой энергией, состоящей из их потенциальной энергии и кинетической энергии . Температура , например, возникает из-за интенсивности случайного движения частиц, вызванного кинетической энергией (известного как броуновское движение ). Когда температура снижается до абсолютного нуля , можно подумать, что всякое движение прекращается и частицы полностью останавливаются. Однако на самом деле кинетическая энергия сохраняется частицами даже при самой низкой возможной температуре. Случайное движение, соответствующее этой нулевой энергии, никогда не исчезает; это следствие принципа неопределенности квантовой механики .

Излучение нулевой точки постоянно передает электрону случайные импульсы , так что он никогда не останавливается полностью. Излучение нулевой точки дает генератору среднюю энергию, равную частоте колебаний, умноженной на половину постоянной Планка .

Принцип неопределенности гласит, что ни один объект не может одновременно иметь точные значения положения и скорости. Полная энергия квантово-механического объекта (потенциальная и кинетическая) описывается его гамильтонианом , который также описывает систему как гармонический осциллятор или волновую функцию , которая колеблется между различными энергетическими состояниями (см. корпускулярно-волновой дуализм ). Все квантовомеханические системы испытывают колебания даже в основном состоянии, что является следствием их волновой природы. Принцип неопределенности требует, чтобы каждая квантовомеханическая система имела флуктуирующую нулевую энергию, превышающую минимум ее классической потенциальной ямы . Это приводит к движению даже при абсолютном нуле. Например, жидкий гелий не замерзает при атмосферном давлении независимо от температуры из-за своей нулевой энергии.

Учитывая эквивалентность массы и энергии, выраженную формулой Альберта Эйнштейна E = mc ² , любую точку в пространстве , содержащую энергию, можно рассматривать как имеющую массу для создания частиц. Виртуальные частицы спонтанно возникают в каждой точке пространства благодаря энергии квантовых флуктуаций, вызванных принципом неопределенности. Современная физика разработала квантовую теорию поля (КТП), чтобы понять фундаментальные взаимодействия между материей и силами. Она рассматривает каждую точку пространства как квантовый гармонический осциллятор . Согласно КТФ, Вселенная состоит из полей материи, квантами которых являются фермионы (т.е. лептоны и кварки), и силовых полей, квантами которых являются бозоны (например, фотоны и глюоны ). Все эти поля имеют нулевую энергию. Недавние эксперименты подтверждают идею о том, что сами частицы можно рассматривать как возбужденные состояния основного квантового вакуума и что все свойства материи являются просто флуктуациями вакуума, возникающими в результате взаимодействия поля нулевой точки.

Идея о том, что «пустое» пространство может иметь связанную с ним внутреннюю энергию и что не существует такой вещи, как «настоящий вакуум», кажется неинтуитивной. Часто утверждают, что вся Вселенная полностью окутана нулевым излучением, и поэтому оно может добавлять лишь некоторую постоянную величину к расчетам. Поэтому физические измерения покажут только отклонения от этого значения. Для многих практических расчетов энергия нулевой точки в математической модели по указу игнорируется как термин, не имеющий физического эффекта. теории относительности Эйнштейна Однако такой подход вызывает проблемы, поскольку в общей значение абсолютной энергии пространства не является произвольной константой и порождает космологическую константу . На протяжении десятилетий большинство физиков предполагали, что существует некий неоткрытый фундаментальный принцип, который устранит бесконечную энергию нулевой точки и заставит ее полностью исчезнуть. Если вакуум не имеет внутренней, абсолютной ценности энергии, он не будет тяготеть. Считалось, что по мере расширения Вселенной после Большого взрыва энергия, содержащаяся в любой единице пустого пространства, будет уменьшаться по мере того, как общая энергия распространяется и заполняет объем Вселенной; галактики и вся материя во Вселенной должны начать замедляться. Эта возможность была исключена в 1998 году открытием того, что расширение Вселенной не замедляется, а на самом деле ускоряется, а это означает, что пустое пространство действительно обладает некоторой внутренней энергией. Открытие Темную энергию лучше всего объяснить энергией нулевой точки, хотя до сих пор остается загадкой, почему ее значение кажется таким маленьким по сравнению с огромным значением, полученным с помощью теории – проблемы космологической постоянной .

Многие физические эффекты, приписываемые энергии нулевой точки, были экспериментально подтверждены, такие как спонтанное излучение , сила Казимира , сдвиг Лэмба , магнитный момент электрона и рассеяние Дельбрюка . Эти эффекты обычно называют «радиационными поправками». В более сложных нелинейных теориях (например, КХД) энергия нулевой точки может вызывать множество сложных явлений, таких как множественные стабильные состояния , нарушение симметрии , хаос и возникновение . Многие физики считают, что «вакуум является ключом к полному пониманию природы». и что его изучение имеет решающее значение в поисках теории всего . Активные области исследований включают эффекты виртуальных частиц, квантовая запутанность , разница (если есть) между инертной и гравитационной массой , изменение скорости света , причина наблюдаемого значения космологической постоянной и природа темной энергии.

История

эфира

Джеймс Клерк Максвелл

Энергия нулевой точки возникла из исторических представлений о вакууме . Для Аристотеля вакуум был τὸ κενόν , «пустой»; т. е. пространство, независимое от тела. Он считал, что эта концепция нарушает основные физические принципы, и утверждал, что элементы огня, воздуха, земли и воды не состоят из атомов, а непрерывны. Для атомистов понятие пустоты носило абсолютный характер: это было различие между существованием и несуществованием. Споры о характеристиках вакуума в основном ограничивались сферой философии , и только намного позже, с началом эпохи Возрождения , Отто фон Герике изобрел первый вакуумный насос и начали появляться первые проверяемые научные идеи. Считалось, что совершенно пустой объем космоса можно создать, просто удалив все газы. Это была первая общепринятая концепция вакуума.

Однако в конце XIX века стало очевидно, что эвакуированный регион все еще содержит тепловое излучение . Существование эфира как замены истинной пустоты было самой распространенной теорией того времени. Согласно успешной теории электромагнитного эфира, основанной на Максвелла электродинамике , этот всеобъемлющий эфир был наделен энергией и, следовательно, сильно отличался от небытия. Тот факт, что электромагнитные и гравитационные явления легко передавались в пустом пространстве, указывал на то, что связанные с ними эфиры были частью ткани самого пространства. Сам Максвелл отмечал, что:

Для тех, кто поддерживал существование пленума как философского принципа, неприязнь природы к вакууму была достаточной причиной для представления о всеокружающем эфире ... Эфиры были изобретены для того, чтобы планеты могли плавать в них, чтобы образовывать электрические атмосферы и магнитные испарения. , чтобы передать ощущения от одной части нашего тела к другой, и так далее, пока пространство не наполнится эфирами три или четыре раза.

Однако результаты эксперимента Майкельсона-Морли в 1887 году стали первым убедительным доказательством того, что распространенные в то время теории эфира имели серьезные недостатки, и положили начало направлению исследований, которые в конечном итоге привели к созданию специальной теории относительности , которая исключила идею стационарного эфира. вообще. Ученым того периода казалось, что настоящий вакуум в космосе можно создать за счет охлаждения и, таким образом, устранения всего излучения и энергии. Из этой идеи возникла вторая концепция достижения настоящего вакуума: охладить область космоса до абсолютной нулевой температуры после вакуумирования. Абсолютного нуля было технически невозможно достичь в XIX веке, поэтому споры остались нерешенными.

Вторая квантовая теория

Планк в 1918 году получил Нобелевскую премию по физике за работы по квантовой теории.

В 1900 году Макс Планк вывел среднюю энергию ε одного излучателя энергии , например, вибрирующей атомной единицы, как функцию абсолютной температуры:

$$\varepsilon ={\frac {h\nu }{e^{h\nu /(kT)}-1}}\,,$$

где h — постоянная Планка , ν — частота , k — постоянная Больцмана , а T — абсолютная температура . Энергия нулевой точки не вносит вклада в первоначальный закон Планка, поскольку в 1900 году Планк не знал о ее существовании.

Концепция нулевой энергии была разработана Максом Планком в Германии в 1911 году как корректирующий термин, добавленный к формуле нулевого заземления, разработанной в его оригинальной квантовой теории в 1900 году.

В 1912 году Макс Планк опубликовал первую журнальную статью, в которой описал прерывистое излучение, основанное на дискретных квантах энергии. Во «второй квантовой теории» Планка резонаторы поглощали энергию непрерывно, но излучали энергию дискретными квантами энергии только тогда, когда они достигали границ конечных ячеек в фазовом пространстве, где их энергии становились целыми кратными hν . Эта теория привела Планка к его новому закону излучения, но в этой версии энергетические резонаторы обладали нулевой энергией, наименьшей средней энергией, которую мог принять резонатор. Уравнение излучения Планка содержало остаточный энергетический фактор, равный единице. hν / 2 , как дополнительный член, зависящий от частоты ν , которая была больше нуля (где h — постоянная Планка). Поэтому широко распространено мнение, что «уравнение Планка ознаменовало рождение концепции энергии нулевой точки». В серии статей с 1911 по 1913 гг. Планк нашел среднюю энергию осциллятора:

$$\varepsilon ={\frac {h\nu }{2}}+{\frac {h\nu }{e^{h\nu /(kT)}-1}}~.$$

Официальный портрет Эйнштейна 1921 года после получения Нобелевской премии по физике.

Вскоре идея нулевой энергии привлекла внимание Альберта Эйнштейна и его помощника Отто Штерна . В 1913 году они опубликовали работу, в которой попытались доказать существование нулевой энергии путем расчета удельной теплоемкости газообразного водорода и сравнили ее с экспериментальными данными. Однако, предположив, что им это удалось, они отказались от поддержки этой идеи вскоре после публикации, поскольку обнаружили, что вторая теория Планка не применима к их примеру. В письме Паулю Эренфесту в том же году Эйнштейн заявил, что энергия нулевой точки «мертва как дверной гвоздь». Энергию нулевой точки также использовал Питер Дебай . который отметил, что нулевая энергия атомов кристаллической решетки будет вызывать уменьшение интенсивности дифрагированного излучения при дифракции рентгеновских лучей даже при приближении температуры к абсолютному нулю. В 1916 году Вальтер Нернст предположил, что пустое пространство заполнено нулевым электромагнитным излучением . С развитием общей теории относительности Эйнштейн обнаружил, что плотность энергии вакуума вносит вклад в космологическую постоянную, чтобы получить статические решения его уравнений поля; идея о том, что пустое пространство или вакуум может иметь некоторую внутреннюю энергию, связанную с ним, вернулась, и Эйнштейн заявил в 1920 году:

В пользу гипотезы эфира можно привести весомый аргумент. Отрицать эфир — значит, в конечном счете, предполагать, что пустое пространство вообще не имеет физических качеств. Фундаментальные факты механики не согласуются с этой точкой зрения... согласно общей теории относительности пространство наделено физическими качествами; следовательно, в этом смысле существует эфир. Согласно общей теории относительности, пространство без эфира немыслимо; ибо в таком пространстве не только не было бы распространения света, но и не было бы возможности существования эталонов пространства и времени (измерительных стержней и часов), а следовательно, и каких-либо пространственно-временных интервалов в физическом смысле. Но этот эфир нельзя рассматривать как наделенный качествами, характерными для весомых сред, как состоящий из частей, которые можно проследить во времени. К нему нельзя применить идею движения.

Гейзенберг, 1924 год.

Курт Бенневиц и Фрэнсис Саймон (1923), работавший в лаборатории Вальтера Нернста в Берлине, изучал процесс плавления химических веществ при низких температурах. Их расчеты температур плавления водорода , аргона и ртути привели их к выводу, что результаты свидетельствуют о нулевой энергии. Более того, они правильно предположили, как позже подтвердил Саймон (1934), что это количество ответственно за трудности затвердевания гелия даже при абсолютном нуле. В 1924 году Роберт Малликен предоставили прямое доказательство нулевой энергии молекулярных колебаний путем сравнения зонного спектра ¹⁰ БО и ¹¹ БО: изотопная разница в частотах перехода между основными колебательными состояниями двух разных электронных уровней исчезла бы, если бы не было нулевой энергии, в отличие от наблюдаемых спектров. Затем, всего год спустя, в 1925 г. с развитием матричной механики в Вернера Гейзенберга статье « Квантово-теоретическая переинтерпретация кинематических и механических соотношений » энергия нулевой точки была получена из квантовой механики.

В 1913 году Нильс Бор предложил то, что сейчас называется Бора . моделью атома но, несмотря на это, оставалось загадкой, почему электроны не попадают в свои ядра. Согласно классическим представлениям, тот факт, что ускоряющийся заряд теряет энергию при излучении, подразумевает, что электрон должен спирально проникнуть в ядро ​​и что атомы не должны быть стабильными. Эту проблему классической механики хорошо резюмировал Джеймс Хопвуд Джинс в 1915 году: «Было бы очень трудно предположить, что закон (силы) 1 / р ² удерживается до нулевых значений r . Ибо силы между двумя зарядами на нулевом расстоянии были бы бесконечными; у нас должны быть заряды противоположного знака, постоянно сталкивающиеся друг с другом, и, когда они будут вместе, никакая сила не будет стремиться превратиться в ничто или бесконечно уменьшаться в размерах». Решение этой загадки пришло в 1926 году, когда Эрвин Шредингер представил уравнение Шрёдингера . Это уравнение объяснило новый, неклассический факт, что электрон, находящийся близко к ядру, обязательно будет иметь большую кинетическую энергию, так что минимальная полная энергия (кинетическая плюс потенциальная) фактически возникает при некотором положительном расстоянии, а не при нулевом расстоянии; другими словами, энергия нулевой точки необходима для атомной стабильности.

Квантовая теория поля

В 1926 году Паскуаль Джордан опубликовал первую попытку квантования электромагнитного поля. В совместной работе с Максом Борном и Вернером Гейзенбергом он рассматривал поле внутри полости как суперпозицию квантовых гармонических осцилляторов. В своих расчетах он обнаружил, что помимо «тепловой энергии» осцилляторов также должен существовать бесконечный энергетический член с нулевой точкой. Ему удалось получить ту же формулу колебаний, которую Эйнштейн получил в 1909 году. Однако Джордан не считал, что его термин бесконечной нулевой энергии был «реальным», написав Эйнштейну, что «это просто величина расчета, не имеющая прямого физического смысла». Джордан нашел способ избавиться от бесконечного члена, опубликовав в 1928 году совместную работу с Паули: выполнение того, что было названо «первым бесконечным вычитанием или перенормировкой в ​​квантовой теории поля».

Поль Дирак, 1933 год.

Основываясь на работах Гейзенберга и других, Поля Дирака (1927 г.) теория излучения и поглощения было первым применением квантовой теории излучения. Работа Дирака считалась чрезвычайно важной для развивающейся области квантовой механики; он имел дело непосредственно с процессом, в котором на самом деле создаются «частицы»: спонтанным излучением . Дирак описал квантование электромагнитного поля как ансамбль гармонических осцилляторов с введением понятия операторов рождения и уничтожения частиц. Теория показала, что спонтанное излучение зависит от нулевых колебаний энергии электромагнитного поля. В процессе аннигиляции (поглощения) фотона можно считать, что фотон переходит в состояние вакуума. Аналогичным образом, когда фотон создается (испускается), иногда полезно представить, что фотон совершил переход из состояния вакуума. По словам Дирака:

Квант света имеет ту особенность, что он, по-видимому, перестает существовать, когда находится в одном из своих стационарных состояний, а именно в нулевом состоянии, в котором его импульс, а следовательно, и энергия, равны нулю. Когда квант света поглощается, можно считать, что он перешел в это нулевое состояние, а когда он испускается, можно считать, что он перепрыгивает из нулевого состояния в то, в котором он физически присутствует, так что кажется, что он был созданный. Поскольку нет предела числу квантов света, которые могут быть созданы таким способом, мы должны предположить, что в нулевом состоянии существует бесконечное число квантов света...

Современные физики, когда их просят дать физическое объяснение спонтанному излучению, обычно ссылаются на нулевую энергию электромагнитного поля. Эту точку зрения популяризировал Виктор Вайскопф, который в 1935 году писал:

Из квантовой теории следует существование так называемых нулевых колебаний; например, каждый осциллятор в своем самом низком состоянии не полностью покоится, а всегда движется около своего положения равновесия. Поэтому электромагнитные колебания также никогда не могут прекратиться полностью. Таким образом, квантовая природа электромагнитного поля имеет своим следствием нулевые колебания напряженности поля в самом низком энергетическом состоянии, в котором нет квантов света в пространстве... Нулевые колебания действуют на электрон так же, как обычные электрические колебания делают. Они могут изменить собственное состояние электрона, но только при переходе в состояние с наименьшей энергией, поскольку пустое пространство может только отнимать энергию, а не отдавать ее. Таким образом, спонтанное излучение возникает как следствие существования этих уникальных напряженностей поля, соответствующих нулевым колебаниям. Таким образом, спонтанное излучение — это индуцированное излучение квантов света, создаваемое нулевыми колебаниями пустого пространства.

Эта точка зрения была позже поддержана Теодором Велтоном (1948), который утверждал, что спонтанное излучение «можно рассматривать как вынужденное излучение, происходящее под действием изменяющегося поля». Эта новая теория, которую Дирак назвал квантовой электродинамикой (КЭД), предсказала флуктуирующее нулевое или «вакуумное» поле, существующее даже в отсутствие источников.

На протяжении 1940-х годов усовершенствования микроволновой технологии позволили проводить более точные измерения сдвига уровней атома водорода , известного теперь как лэмбовский сдвиг. и измерение магнитного момента электрона. Расхождения между этими экспериментами и теорией Дирака привели к идее включения перенормировки в КЭД для решения проблем нулевой бесконечности. Перенормировка была первоначально разработана Гансом Крамерсом. а также Виктор Вайскопф (1936), (1947) для вычисления конечного значения лэмбовского сдвига и впервые успешно применён Гансом Бете . Что касается спонтанного излучения, эти эффекты частично можно объяснить взаимодействием с полем нулевой точки. Но в свете того, что перенормировка позволила удалить из вычислений некоторые нулевые бесконечности, не все физики были готовы приписывать нулевой энергии какой-либо физический смысл, рассматривая ее вместо этого как математический артефакт, который однажды может быть устранен. В Вольфганга Паули 1945 года Нобелевской лекции он ясно выразил свое несогласие с идеей нулевой энергии, заявив: «Ясно, что эта нулевая энергия не имеет физической реальности».

Хендрик Казимир (1958)

В 1948 году Хендрик Казимир. показал, что одним из последствий нулевого поля является сила притяжения между двумя незаряженными, идеально проводящими параллельными пластинами, так называемый эффект Казимира. В то время Казимир изучал свойства коллоидных растворов . Это вязкие материалы, такие как краска и майонез, которые содержат частицы микронного размера в жидкой матрице. Свойства таких растворов определяются силами Ван-дер-Ваальса – короткодействующими силами притяжения, существующими между нейтральными атомами и молекулами. Один из коллег Казимира, Тео Овербек, понял, что теория, которая использовалась в то время для объяснения сил Ван дер Ваальса и была разработана Фрицем Лондоном в 1930 году, не объяснил должным образом экспериментальные измерения на коллоидах. Поэтому Овербек попросил Казимира разобраться в этой проблеме. Работая с Дирком Полдером , Казимир обнаружил, что взаимодействие между двумя нейтральными молекулами можно правильно описать только в том случае, если принять во внимание тот факт, что свет распространяется с конечной скоростью. Вскоре после разговора с Бором об энергии нулевой точки Казимир заметил, что этот результат можно интерпретировать в терминах вакуумных флуктуаций. Затем он спросил себя, что произошло бы, если бы в вакууме было два зеркала, а не две молекулы, обращенные друг к другу. Именно эта работа привела его к предсказанию силы притяжения между отражающими пластинами. Работа Казимира и Польдера открыла путь к единой теории сил Ван дер Ваальса и Казимира и плавному континууму между этими двумя явлениями. Это сделал Лифшиц (1956). в случае плоскопараллельных диэлектрических пластин . Общее название сил Ван-дер-Ваальса и Казимира — дисперсионные силы, поскольку обе они вызваны дисперсией оператора дипольного момента. Роль релятивистских сил становится доминирующей на порядках сотен нанометров.

В 1951 году Герберт Каллен и Теодор Велтон. доказал квантовую теорему о флуктуации-диссипации (FDT), которая первоначально была сформулирована в классической форме Найквистом (1928). как объяснение наблюдаемого шума Джонсона в электрических цепях. Теорема о флуктуации-диссипации показала, что когда что-то рассеивает энергию фактически необратимым образом, подключенная тепловая ванна также должна колебаться. Колебания и диссипация идут рука об руку; невозможно иметь одно без другого. Смысл FDT заключается в том, что вакуум можно рассматривать как тепловую ванну, соединенную с диссипативной силой, и поэтому энергию можно частично извлечь из вакуума для потенциально полезной работы. Экспериментально было показано, что FDT верен при определенных квантовых, неклассических условиях.

В 1963 году модель Джейнса – Каммингса была разработана для описания системы двухуровневого атома, взаимодействующего с модой квантованного поля (т.е. вакуумом) внутри оптического резонатора. Он дал неинтуитивные предсказания, например, что спонтанное излучение атома может быть вызвано полем практически постоянной частоты ( частота Раби ). В 1970-х годах проводились эксперименты по проверке аспектов квантовой оптики, которые показали, что скоростью спонтанного излучения атома можно управлять с помощью отражающих поверхностей. В некоторых кругах к этим результатам сначала отнеслись с подозрением: утверждалось, что никакое изменение скорости спонтанного излучения невозможно, в конце концов, как на излучение фотона может влиять окружение атома, если атом может только «видеть»? «Окружающая среда, в первую очередь, испуская фотон? Эти эксперименты положили начало квантовой электродинамике полостей (CQED), изучению влияния зеркал и резонаторов на радиационные поправки. Спонтанное излучение можно подавлять (или «ингибировать»). или усиленный. Усиление было впервые предсказано Перселлом в 1946 году. ( эффект Перселла ) и было подтверждено экспериментально. Частично это явление можно понять с точки зрения действия вакуумного поля на атом.

Принцип неопределенности

Основная статья: Принцип неопределенности

Энергия нулевой точки фундаментально связана с принципом неопределенности Гейзенберга. частицы Грубо говоря, принцип неопределенности гласит, что дополнительные переменные (такие как положение и импульс или значение поля и производная в точке пространства) не могут одновременно точно определяться каким-либо заданным квантовым состоянием. В частности, не может существовать состояния, в котором система просто неподвижно сидит на дне своей потенциальной ямы, поскольку тогда ее положение и импульс были бы полностью определены со сколь угодно большой точностью. Следовательно, состояние с наименьшей энергией (основное состояние) системы должно иметь распределение по положению и импульсу, которое удовлетворяет принципу неопределенности, который подразумевает, что его энергия должна быть больше минимума потенциальной ямы.

Вблизи дна потенциальной ямы гамильтониан , общей системы (квантово-механический оператор задающий ее энергию) можно аппроксимировать как квантовый гармонический осциллятор :

$${\hat {H}}=V_{0}+{\tfrac {1}{2}}k\left({\hat {x}}-x_{0}\right)^{2}+{\frac {1}{2m}}{\hat {p}}^{2}\,,$$

где V ₀ — минимум классической потенциальной ямы.

Принцип неопределенности говорит нам, что

$${\sqrt {\left\langle \left({\hat {x}}-x_{0}\right)^{2}\right\rangle }}{\sqrt {\left\langle {\hat {p}}^{2}\right\rangle }}\geq {\frac {\hbar }{2}}\,,$$

чтобы средние значения приведенных выше кинетических и потенциальных членов удовлетворяли

$$\left\langle {\tfrac {1}{2}}k\left({\hat {x}}-x_{0}\right)^{2}\right\rangle \left\langle {\frac {1}{2m}}{\hat {p}}^{2}\right\rangle \geq \left({\frac {\hbar }{4}}\right)^{2}{\frac {k}{m}}\,.$$

Поэтому математическое ожидание энергии должно быть не менее

$$\left\langle {\hat {H}}\right\rangle \geq V_{0}+{\frac {\hbar }{2}}{\sqrt {\frac {k}{m}}}=V_{0}+{\frac {\hbar \omega }{2}}$$

где ω = √k , / m — угловая частота с которой колеблется система.

Более тщательное рассмотрение, показывающее, что энергия основного состояния действительно насыщает эту границу и равна точно E ₀ = V ₀ + ħω / 2 требует решения основного состояния системы.

Атомная физика

Основная статья: Основное состояние

Нулевая энергия E = ħω / 2 заставляет основное состояние гармонического осциллятора опережать свою фазу (цвет). Это имеет измеримый эффект, когда несколько собственных состояний накладываются друг на друга.

Идея квантового гармонического осциллятора и связанной с ним энергии может быть применима как к атому, так и к субатомной частице. В обычной атомной физике энергия нулевой точки — это энергия, связанная с основным состоянием системы. В профессиональной литературе по физике частота, обозначенная выше как ν , имеет тенденцию измеряться с использованием угловой частоты , обозначаемой ω и определяемой как ω = 2 πν . Это приводит к соглашению писать постоянную Планка h с чертой сверху ( ħ ) для обозначения величины ч / 2π . В этих терминах примером энергии нулевой точки является приведенное выше E = ħω / 2 связано с основным состоянием квантового гармонического осциллятора. С точки зрения квантовой механики энергия нулевой точки — это математическое ожидание гамильтониана системы в основном состоянии.

Если существует более одного основного состояния, то они называются вырожденными . Многие системы имеют вырожденные основные состояния. Вырождение происходит всякий раз, когда существует унитарный оператор , который нетривиально действует на основном состоянии и коммутирует с гамильтонианом системы.

Согласно третьему закону термодинамики , система при абсолютной нулевой температуре существует в основном состоянии; таким образом, его энтропия определяется вырождением основного состояния. Многие системы, такие как идеальная кристаллическая решетка , имеют уникальное основное состояние и, следовательно, имеют нулевую энтропию при абсолютном нуле. Также возможно, что высшее возбужденное состояние будет иметь абсолютную нулевую температуру для систем с отрицательной температурой .

Волновая функция основного состояния частицы в одномерной яме представляет собой полупериодическую синусоидальную волну , стремящуюся к нулю на двух краях ямы. Энергия частицы определяется выражением:

$${\frac {h^{2}n^{2}}{8mL^{2}}}$$

где h — постоянная Планка , m — масса частицы, n — энергетическое состояние ( n = 1 соответствует энергии основного состояния), а L — ширина ямы.

Квантовая теория поля

Основные статьи: Ожидаемое значение вакуума , Энергия вакуума и Состояние вакуума.

В квантовой теории поля (КТП) ткань «пустого» пространства визуализируется как состоящая из полей , причем поле в каждой точке пространства и времени представляет собой квантовый гармонический осциллятор, а соседние осцилляторы взаимодействуют друг с другом. Согласно КТП, Вселенная состоит из полей материи, квантами которых являются фермионы (например, электроны и кварки), силовых полей, квантами которых являются бозоны (т.е. фотоны и глюоны), и поля Хиггса, квантом которого является бозон Хиггса . Материя и силовые поля имеют нулевую энергию. Связанный с этим термин — поле нулевой точки (ZPF), которое представляет собой состояние с наименьшей энергией определенного поля. Вакуум можно рассматривать не как пустое пространство, а как совокупность всех нулевых полей.

В КТП энергия нулевой точки вакуумного состояния называется энергией вакуума, а среднее математическое ожидание гамильтониана называется вакуумным математическим ожиданием (также называемым конденсатом или просто VEV). Вакуум КЭД является частью вакуумного состояния, которое конкретно занимается квантовой электродинамикой (например, электромагнитными взаимодействиями между фотонами, электронами и вакуумом), а вакуум КХД имеет дело с квантовой хромодинамикой (например, взаимодействием цветовых зарядов между кварками, глюонами и вакуумом). Недавние эксперименты поддерживают идею о том, что сами частицы можно рассматривать как возбужденные состояния основного квантового вакуума и что все свойства материи являются просто флуктуациями вакуума, возникающими в результате взаимодействия с полем нулевой точки.

Каждая точка пространства вносит вклад E = ħω / 2 , что приводит к вычислению бесконечной нулевой энергии в любом конечном объеме; это одна из причин, по которой перенормировка необходима, чтобы понять смысл квантовых теорий поля. В космологии энергия вакуума является одним из возможных объяснений космологической постоянной. и источник темной энергии.

Ученые не пришли к единому мнению относительно того, сколько энергии содержится в вакууме. Квантовая механика требует, чтобы энергия была большой, как утверждал Поль Дирак , — как море энергии . Другие ученые, специализирующиеся на общей теории относительности, требуют, чтобы энергия была достаточно малой, чтобы кривизна пространства соответствовала наблюдениям астрономии . Принцип неопределенности Гейзенберга позволяет энергии быть настолько большой, насколько это необходимо для обеспечения квантовых действий в течение короткого момента времени, даже если средняя энергия достаточно мала, чтобы удовлетворить теории относительности и плоского пространства. Чтобы справиться с разногласиями, энергия вакуума описывается как виртуальный энергетический потенциал положительной и отрицательной энергии.

В квантовой теории возмущений иногда говорят, что вклад однопетлевых и многопетлевых диаграмм Фейнмана в элементарных частиц пропагаторы — это вклад вакуумных флуктуаций или энергии нулевой точки в массы частиц .

вакуум

Основная статья: вакуум QED

Самым старым и самым известным квантованным силовым полем является электромагнитное поле . Уравнения Максвелла были заменены квантовой электродинамикой (КЭД). Рассматривая энергию нулевой точки, возникающую в результате КЭД, можно получить характерное понимание энергии нулевой точки, которая возникает не только в результате электромагнитных взаимодействий, но и во всех квантовых теориях поля .

энергии

В квантовой теории электромагнитного поля классические волновые амплитуды α и α * заменяются операторами а и а. ^† которые удовлетворяют:

$$\left[a,a^{\dagger }\right]=1$$

Классическая величина | α | ² фигурирующий в классическом выражении для энергии полевой моды, в квантовой теории заменяется оператором числа фотонов a ^† а . Тот факт, что:

$$\left[a,a^{\dagger }a\right]\neq 1$$

подразумевает, что квантовая теория не допускает состояний поля излучения, для которых число фотонов и амплитуда поля могут быть точно определены, т. е. мы не можем иметь одновременные собственные состояния для ^† а и а . Согласование волновых и корпускулярных атрибутов поля достигается посредством ассоциации амплитуды вероятности с классической картиной мод. Расчет мод поля представляет собой вполне классическую задачу, а квантовые свойства поля передаются «амплитудами» мод . ^† и связанный с этими классическими модами.

Нулевая энергия поля формально возникает из некоммутативности a и a. ^† . Это верно для любого гармонического осциллятора: энергия нулевой точки ħω / 2 появляется, когда мы записываем гамильтониан:

$${\begin{aligned}H_{cl}&={\frac {p^{2}}{2m}}+{\tfrac {1}{2}}m\omega ^{2}{q}^{2}\\&={\tfrac {1}{2}}\hbar \omega \left(aa^{\dagger }+a^{\dagger }a\right)\\&=\hbar \omega \left(a^{\dagger }a+{\tfrac {1}{2}}\right)\end{aligned}}$$

Часто утверждают, что вся Вселенная полностью окутана нулевым электромагнитным полем, и поэтому оно может добавлять лишь некоторую постоянную величину к ожидаемым значениям. Поэтому физические измерения покажут только отклонения от состояния вакуума. Таким образом, энергию нулевой точки можно исключить из гамильтониана, переопределив ноль энергии или утверждая, что она является константой и, следовательно, не оказывает влияния на уравнения движения Гейзенберга. Таким образом, мы можем объявить постановлением, что основное состояние имеет нулевую энергию, а гамильтониан поля, например, можно заменить следующим:

$${\begin{aligned}H_{F}-\left\langle 0|H_{F}|0\right\rangle &={\tfrac {1}{2}}\hbar \omega \left(aa^{\dagger }+a^{\dagger }a\right)-{\tfrac {1}{2}}\hbar \omega \\&=\hbar \omega \left(a^{\dagger }a+{\tfrac {1}{2}}\right)-{\tfrac {1}{2}}\hbar \omega \\&=\hbar \omega a^{\dagger }a\end{aligned}}$$

не затрагивая никаких физических предсказаний теории. Говорят, что новый гамильтониан является нормально упорядоченным (или упорядоченным по Вику) и обозначается символом двойной точки. Нормально упорядоченный гамильтониан обозначается : HF _{, т.е} .:

$$:H_{F}:\equiv \hbar \omega \left(aa^{\dagger }+a^{\dagger }a\right):\equiv \hbar \omega a^{\dagger }a$$

Другими словами, внутри обычного символа упорядочивания мы можем коммутировать a и a. ^† . Поскольку энергия нулевой точки тесно связана с некоммутативностью a и a ^† , нормальная процедура упорядочивания исключает любой вклад поля нулевой точки. Это особенно разумно в случае гамильтониана поля, поскольку нулевой член просто добавляет постоянную энергию, которую можно устранить простым переопределением нуля энергии. Более того, эта постоянная энергия в гамильтониане, очевидно, коммутирует с a и a ^† и поэтому не может иметь никакого влияния на квантовую динамику, описываемую уравнениями движения Гейзенберга.

Однако все не так просто. Энергию нулевой точки нельзя исключить, исключив ее энергию из гамильтониана: когда мы делаем это и решаем уравнение Гейзенберга для оператора поля, мы должны включить вакуумное поле, которое является однородной частью решения для оператора поля. Фактически мы можем показать, что вакуумное поле существенно для сохранения коммутаторов и формальной непротиворечивости КЭД. Когда мы вычисляем энергию поля, мы получаем не только вклад от частиц и сил, которые могут присутствовать, но также вклад от самого вакуумного поля, то есть энергию поля в нулевой точке. Другими словами, энергия нулевой точки появляется снова, даже если мы удалили ее из гамильтониана.

Электромагнитное поле в свободном пространстве

Из уравнений Максвелла электромагнитная энергия «свободного» поля, то есть поля без источников, описывается следующим образом:

$${\begin{aligned}H_{F}&={\frac {1}{8\pi }}\int d^{3}r\left(\mathbf {E} ^{2}+\mathbf {B} ^{2}\right)\\&={\frac {k^{2}}{2\pi }}|\alpha (t)|^{2}\end{aligned}}$$

Введем «модовую функцию» A0 _{удовлетворяющую} ( r ), уравнению Гельмгольца :

$$\left(\nabla ^{2}+k^{2}\right)\mathbf {A} _{0}(\mathbf {r} )=0$$

где к = ω / c и предположим, что оно нормировано так, что:

$$\int d^{3}r\left|\mathbf {A} _{0}(\mathbf {r} )\right|^{2}=1$$

Мы хотим «квантовать» электромагнитную энергию свободного пространства для многомодового поля. Напряженность поля свободного пространства должна быть независимой от положения, так что | А ₀ ( р ) | ² должна быть независима от r для каждой моды поля. Функция режима, удовлетворяющая этим условиям:

$$\mathbf {A} _{0}(\mathbf {r} )=e_{\mathbf {k} }e^{i\mathbf {k} \cdot \mathbf {r} }$$

где k · e _k = 0, чтобы обеспечить выполнение условия трансверсальности ∇ · A ( r , t ) для кулоновской калибровки в котором мы работаем.

Чтобы добиться желаемой нормализации, мы притворяемся, что пространство разделено на кубы объёмом V = L. ³ и наложим на поле периодическое граничное условие:

$$\mathbf {A} (x+L,y+L,z+L,t)=\mathbf {A} (x,y,z,t)$$

или эквивалентно

$$\left(k_{x},k_{y},k_{z}\right)={\frac {2\pi }{L}}\left(n_{x},n_{y},n_{z}\right)$$

где n может принимать любое целочисленное значение. Это позволяет нам рассмотреть поле в любом из воображаемых кубов и определить функцию режима:

$$\mathbf {A} _{\mathbf {k} }(\mathbf {r} )={\frac {1}{\sqrt {V}}}e_{\mathbf {k} }e^{i\mathbf {k} \cdot \mathbf {r} }$$

которое удовлетворяет уравнению Гельмгольца, трансверсальности и «нормализации ящика»:

$$\int _{V}d^{3}r\left|\mathbf {A} _{\mathbf {k} }(\mathbf {r} )\right|^{2}=1$$

где e _k выбран в качестве единичного вектора, который задает поляризацию моды поля. Условие k · e _k = 0 что существует два независимых выбора , _ek называем ek _{мы 1} и ek _{где 2,} ek 1 _{· означает ,} ek 2 _{= которые} 0 и e ²
_{к 1} = е ²
_{к 2} знак равно 1 . Таким образом, мы определяем функции режима:

$$\mathbf {A} _{\mathbf {k} \lambda }(\mathbf {r} )={\frac {1}{\sqrt {V}}}e_{\mathbf {k} \lambda }e^{i\mathbf {k} \cdot \mathbf {r} }\,,\quad \lambda ={\begin{cases}1\\2\end{cases}}$$

в рамках которого векторный потенциал становится :

$$\mathbf {A} _{\mathbf {k} \lambda }(\mathbf {r} ,t)={\sqrt {\frac {2\pi \hbar c^{2}}{\omega _{k}V}}}\left[a_{\mathbf {k} \lambda }(0)e^{i\mathbf {k} \cdot \mathbf {r} }+a_{\mathbf {k} \lambda }^{\dagger }(0)e^{-i\mathbf {k} \cdot \mathbf {r} }\right]e_{\mathbf {k} \lambda }$$

или:

$$\mathbf {A} _{\mathbf {k} \lambda }(\mathbf {r} ,t)={\sqrt {\frac {2\pi \hbar c^{2}}{\omega _{k}V}}}\left[a_{\mathbf {k} \lambda }(0)e^{-i(\omega _{k}t-\mathbf {k} \cdot \mathbf {r} )}+a_{\mathbf {k} \lambda }^{\dagger }(0)e^{i(\omega _{k}t-\mathbf {k} \cdot \mathbf {r} )}\right]$$

где ω _k = kc и a _{k λ} , a ^†
_{k λ} – операторы уничтожения и рождения фотонов для моды с волновым вектором k и поляризацией λ . Это дает векторный потенциал для плосковолновой моды поля. Условие для ( k _x , ky _, показывает , k _z ) что таких режимов бесконечно много. Линейность уравнений Максвелла позволяет записать:

$$\mathbf {A} (\mathbf {r} t)=\sum _{\mathbf {k} \lambda }{\sqrt {\frac {2\pi \hbar c^{2}}{\omega _{k}V}}}\left[a_{\mathbf {k} \lambda }(0)e^{i\mathbf {k} \cdot \mathbf {r} }+a_{\mathbf {k} \lambda }^{\dagger }(0)e^{-i\mathbf {k} \cdot \mathbf {r} }\right]e_{\mathbf {k} \lambda }$$

для полного векторного потенциала в свободном пространстве. Используя тот факт, что:

$$\int _{V}d^{3}r\mathbf {A} _{\mathbf {k} \lambda }(\mathbf {r} )\cdot \mathbf {A} _{\mathbf {k} '\lambda '}^{\ast }(\mathbf {r} )=\delta _{\mathbf {k} ,\mathbf {k} '}^{3}\delta _{\lambda ,\lambda '}$$

мы находим, что гамильтониан поля:

$$H_{F}=\sum _{\mathbf {k} \lambda }\hbar \omega _{k}\left(a_{\mathbf {k} \lambda }^{\dagger }a_{\mathbf {k} \lambda }+{\tfrac {1}{2}}\right)$$

Это гамильтониан для бесконечного числа несвязанных гармонических осцилляторов. Таким образом, разные моды поля независимы и удовлетворяют коммутационным соотношениям:

$${\begin{aligned}\left[a_{\mathbf {k} \lambda }(t),a_{\mathbf {k} '\lambda '}^{\dagger }(t)\right]&=\delta _{\mathbf {k} ,\mathbf {k} '}^{3}\delta _{\lambda ,\lambda '}\\[10px]\left[a_{\mathbf {k} \lambda }(t),a_{\mathbf {k} '\lambda '}(t)\right]&=\left[a_{\mathbf {k} \lambda }^{\dagger }(t),a_{\mathbf {k} '\lambda '}^{\dagger }(t)\right]=0\end{aligned}}$$

Очевидно, что наименьшее собственное значение для HF _равно :

$$\sum _{\mathbf {k} \lambda }{\tfrac {1}{2}}\hbar \omega _{k}$$

Это состояние описывает нулевую энергию вакуума. Похоже, что эта сумма расходится – на самом деле сильно расходится, если добавить коэффициент плотности.

$${\frac {8\pi v^{2}dv}{c^{3}}}V$$

шоу. Сумма становится приблизительно интегральной:

$${\frac {4\pi hV}{c^{3}}}\int v^{3}\,dv$$

для высоких значений v . Он расходится пропорционально v ⁴ для большого v .

Необходимо рассмотреть два отдельных вопроса. Во-первых, является ли дивергенция реальной, так что энергия нулевой точки действительно бесконечна? Если учесть, что объем V содержится в идеально проводящих стенках, то очень высокие частоты можно удержать только за счет все более и более совершенной проводимости. Никакой реальный метод сдерживания высоких частот невозможен. Такие моды не будут стационарными в нашем ящике и, следовательно, не будут учитываться по стационарному содержанию энергии. Таким образом, с этой физической точки зрения приведенная выше сумма должна распространяться только на те частоты, которые являются счетными; Таким образом, отключение энергии в высшей степени разумно. Однако в масштаб «вселенной» должны быть включены вопросы общей теории относительности. Предположим, что даже коробки можно было бы воспроизвести, соединить вместе и красиво закрыть, искривив пространство-время. Тогда могут быть возможны точные условия для бегущих волн. Однако кванты очень высокой частоты все равно не будут удержаны. По «геонам» Джона Уиллера. они вытекут из системы. Итак, снова отсечение допустимо, почти необходимо. Здесь возникает вопрос о последовательности, поскольку кванты очень высокой энергии будут действовать как источник массы и начнут искривлять геометрию.

Это приводит ко второму вопросу. Расходящаяся или нет, конечная или бесконечная, имеет ли энергия нулевой точки какое-либо физическое значение? Во всех практических расчетах часто рекомендуется игнорировать всю энергию нулевой точки. Причина этого в том, что энергии обычно определяются не произвольной точкой данных, а скорее изменениями в точках данных, поэтому следует разрешить добавление или вычитание константы (даже если она бесконечна). Однако это еще не все, на самом деле энергия определяется не так произвольно: в общей теории относительности источником искривления пространства-времени является энергетическое содержание, и здесь абсолютное количество энергии имеет реальный физический смысл. Не существует такого понятия, как произвольная аддитивная константа с плотностью энергии поля. Плотность энергии искривляет пространство, а увеличение плотности энергии приводит к увеличению кривизны. Более того, нулевая плотность энергии имеет и другие физические последствия, например, эффект Казимира, вклад в лэмбовский сдвиг или аномальный магнитный момент электрона. Ясно, что это не просто математическая константа или артефакт, который можно устранить.

вакуумного поля

Вакуумное состояние «свободного» электромагнитного поля (без источников) определяется как основное состояние, в котором λ _{nk =} 0 для всех мод ( k , λ ) . Вакуумное состояние, как и все стационарные состояния поля, является собственным состоянием гамильтониана, а не операторов электрического и магнитного поля. Поэтому в вакуумном состоянии электрические и магнитные поля не имеют определенных значений. Мы можем представить, что они колеблются около своего среднего значения, равного нулю.

В процессе аннигиляции (поглощения) фотона можно думать, что фотон переходит в состояние вакуума. Аналогичным образом, когда фотон создается (испускается), иногда полезно представить, что фотон совершил переход из состояния вакуума. Атом, например, можно считать «одетым» за счет испускания и реабсорбции «виртуальных фотонов» из вакуума. Энергия вакуумного состояния, описываемая Σ _{k λ} ħω _k / 2 бесконечно. Мы можем произвести замену:

$$\sum _{\mathbf {k} \lambda }\longrightarrow \sum _{\lambda }\left({\frac {1}{2\pi }}\right)^{3}\int d^{3}k={\frac {V}{8\pi ^{3}}}\sum _{\lambda }\int d^{3}k$$

the zero-point energy density is:

$${\begin{aligned}{\frac {1}{V}}\sum _{\mathbf {k} \lambda }{\tfrac {1}{2}}\hbar \omega _{k}&={\frac {2}{8\pi ^{3}}}\int d^{3}k{\tfrac {1}{2}}\hbar \omega _{k}\\&={\frac {4\pi }{4\pi ^{3}}}\int dk\,k^{2}\left({\tfrac {1}{2}}\hbar \omega _{k}\right)\\&={\frac {\hbar }{2\pi ^{2}c^{3}}}\int d\omega \,\omega ^{3}\end{aligned}}$$

or in other words the spectral energy density of the vacuum field:

$$\rho _{0}(\omega )={\frac {\hbar \omega ^{3}}{2\pi ^{2}c^{3}}}$$

The zero-point energy density in the frequency range from ω₁ to ω₂ is therefore:

$$\int _{\omega _{1}}^{\omega _{2}}d\omega \rho _{0}(\omega )={\frac {\hbar }{8\pi ^{2}c^{3}}}\left(\omega _{2}^{4}-\omega _{1}^{4}\right)$$

This can be large even in relatively narrow "low frequency" regions of the spectrum. In the optical region from 400 to 700 nm, for instance, the above equation yields around 220 erg/cm³.

We showed in the above section that the zero-point energy can be eliminated from the Hamiltonian by the normal ordering prescription. However, this elimination does not mean that the vacuum field has been rendered unimportant or without physical consequences. To illustrate this point we consider a linear dipole oscillator in the vacuum. The Hamiltonian for the oscillator plus the field with which it interacts is:

$$H={\frac {1}{2m}}\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)^{2}+{\tfrac {1}{2}}m\omega _{0}^{2}\mathbf {x} ^{2}+H_{F}$$

This has the same form as the corresponding classical Hamiltonian and the Heisenberg equations of motion for the oscillator and the field are formally the same as their classical counterparts. For instance the Heisenberg equations for the coordinate x and the canonical momentum p = mẋ +eA/c of the oscillator are:

$${\begin{aligned}\mathbf {\dot {x}} &=(i\hbar )^{-1}[\mathbf {x} .H]={\frac {1}{m}}\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)\\\mathbf {\dot {p}} &=(i\hbar )^{-1}[\mathbf {p} .H]{\begin{aligned}&={\tfrac {1}{2}}\nabla \left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)^{2}-m\omega _{0}^{2}\mathbf {\dot {x}} \\&=-{\frac {1}{m}}\left[\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)\cdot \nabla \right]\left[-{\frac {e}{c}}\mathbf {A} \right]-{\frac {1}{m}}\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)\times \nabla \times \left[-{\frac {e}{c}}\mathbf {A} \right]-m\omega _{0}^{2}\mathbf {\dot {x}} \\&={\frac {e}{c}}(\mathbf {\dot {x}} \cdot \nabla )\mathbf {A} +{\frac {e}{c}}\mathbf {\dot {x}} \times \mathbf {B} -m\omega _{0}^{2}\mathbf {\dot {x}} \end{aligned}}\end{aligned}}$$

or:

$${\begin{aligned}m\mathbf {\ddot {x}} &=\mathbf {\dot {p}} -{\frac {e}{c}}\mathbf {\dot {A}} \\&=-{\frac {e}{c}}\left[\mathbf {\dot {A}} -\left(\mathbf {\dot {x}} \cdot \nabla \right)\mathbf {A} \right]+{\frac {e}{c}}\mathbf {\dot {x}} \times \mathbf {B} -m\omega _{0}^{2}\mathbf {x} \\&=e\mathbf {E} +{\frac {e}{c}}\mathbf {\dot {x}} \times \mathbf {B} -m\omega _{0}^{2}\mathbf {x} \end{aligned}}$$

since the rate of change of the vector potential in the frame of the moving charge is given by the convective derivative

$$\mathbf {\dot {A}} ={\frac {\partial \mathbf {A} }{\partial t}}+(\mathbf {\dot {x}} \cdot \nabla )\mathbf {A} ^{3}\,.$$

For nonrelativistic motion we may neglect the magnetic force and replace the expression for mẍ by:

$${\begin{aligned}\mathbf {\ddot {x}} +\omega _{0}^{2}\mathbf {x} &\approx {\frac {e}{m}}\mathbf {E} \\&\approx \sum _{\mathbf {k} \lambda }{\sqrt {\frac {2\pi \hbar \omega _{k}}{V}}}\left[a_{\mathbf {k} \lambda }(t)+a_{\mathbf {k} \lambda }^{\dagger }(t)\right]e_{\mathbf {k} \lambda }\end{aligned}}$$

Above we have made the electric dipole approximation in which the spatial dependence of the field is neglected. The Heisenberg equation for a_kλ is found similarly from the Hamiltonian to be:

$${\dot {a}}_{\mathbf {k} \lambda }=i\omega _{k}a_{\mathbf {k} \lambda }+ie{\sqrt {\frac {2\pi }{\hbar \omega _{k}V}}}\mathbf {\dot {x}} \cdot e_{\mathbf {k} \lambda }$$

in the electric dipole approximation.

In deriving these equations for x, p, and a_kλ we have used the fact that equal-time particle and field operators commute. This follows from the assumption that particle and field operators commute at some time (say, t = 0) when the matter-field interpretation is presumed to begin, together with the fact that a Heisenberg-picture operator A(t) evolves in time as A(t) = U^†(t)A(0)U(t), where U(t) is the time evolution operator satisfying

$$i\hbar {\dot {U}}=HU\,,\quad U^{\dagger }(t)=U^{-1}(t)\,,\quad U(0)=1\,.$$

Alternatively, we can argue that these operators must commute if we are to obtain the correct equations of motion from the Hamiltonian, just as the corresponding Poisson brackets in classical theory must vanish in order to generate the correct Hamilton equations. The formal solution of the field equation is:

$$a_{\mathbf {k} \lambda }(t)=a_{\mathbf {k} \lambda }(0)e^{-i\omega _{k}t}+ie{\sqrt {\frac {2\pi }{\hbar \omega _{k}V}}}\int _{0}^{t}dt'\,e_{\mathbf {k} \lambda }\cdot \mathbf {\dot {x}} (t')e^{i\omega _{k}\left(t'-t\right)}$$

and therefore the equation for ȧ_kλ may be written:

$$\mathbf {\ddot {x}} +\omega _{0}^{2}\mathbf {x} ={\frac {e}{m}}\mathbf {E} _{0}(t)+{\frac {e}{m}}\mathbf {E} _{RR}(t)$$

where

$$\mathbf {E} _{0}(t)=i\sum _{\mathbf {k} \lambda }{\sqrt {\frac {2\pi \hbar \omega _{k}}{V}}}\left[a_{\mathbf {k} \lambda }(0)e^{-i\omega _{k}t}-a_{\mathbf {k} \lambda }^{\dagger }(0)e^{i\omega _{k}t}\right]e_{\mathbf {k} \lambda }$$

and

$$\mathbf {E} _{RR}(t)=-{\frac {4\pi e}{V}}\sum _{\mathbf {k} \lambda }\int _{0}^{t}dt'\left[e_{\mathbf {k} \lambda }\cdot \mathbf {\dot {x}} \left(t'\right)\right]\cos \omega _{k}\left(t'-t\right)$$

It can be shown that in the radiation reaction field, if the mass m is regarded as the "observed" mass then we can take

$$\mathbf {E} _{RR}(t)={\frac {2e}{3c^{3}}}\mathbf {\ddot {x}}$$

The total field acting on the dipole has two parts, E₀(t) and E_RR(t). E₀(t) is the free or zero-point field acting on the dipole. It is the homogeneous solution of the Maxwell equation for the field acting on the dipole, i.e., the solution, at the position of the dipole, of the wave equation

$$\left[\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right]\mathbf {E} =0$$

satisfied by the field in the (source free) vacuum. For this reason E₀(t) is often referred to as the "vacuum field", although it is of course a Heisenberg-picture operator acting on whatever state of the field happens to be appropriate at t = 0. E_RR(t) is the source field, the field generated by the dipole and acting on the dipole.

Using the above equation for E_RR(t) we obtain an equation for the Heisenberg-picture operator $\mathbf {x} (t)$ that is formally the same as the classical equation for a linear dipole oscillator:

$$\mathbf {\ddot {x}} +\omega _{0}^{2}\mathbf {x} -\tau \mathbf {\overset {...}{x}} ={\frac {e}{m}}\mathbf {E} _{0}(t)$$

where τ = 2e²/3mc³. in this instance we have considered a dipole in the vacuum, without any "external" field acting on it. the role of the external field in the above equation is played by the vacuum electric field acting on the dipole.

Classically, a dipole in the vacuum is not acted upon by any "external" field: if there are no sources other than the dipole itself, then the only field acting on the dipole is its own radiation reaction field. In quantum theory however there is always an "external" field, namely the source-free or vacuum field E₀(t).

According to our earlier equation for a_kλ(t) the free field is the only field in existence at t = 0 as the time at which the interaction between the dipole and the field is "switched on". The state vector of the dipole-field system at t = 0 is therefore of the form

$$|\Psi \rangle =|{\text{vac}}\rangle |\psi _{D}\rangle \,,$$

where |vac⟩ is the vacuum state of the field and |ψ_D⟩ is the initial state of the dipole oscillator. The expectation value of the free field is therefore at all times equal to zero:

$$\langle \mathbf {E} _{0}(t)\rangle =\langle \Psi |\mathbf {E} _{0}(t)|\Psi \rangle =0$$

since a_kλ(0)|vac⟩ = 0. however, the energy density associated with the free field is infinite:

$${\begin{aligned}{\frac {1}{4\pi }}\left\langle \mathbf {E} _{0}^{2}(t)\right\rangle &={\frac {1}{4\pi }}\sum _{\mathbf {k} \lambda }\sum _{\mathbf {k'} \lambda '}{\sqrt {\frac {2\pi \hbar \omega _{k}}{V}}}{\sqrt {\frac {2\pi \hbar \omega _{k'}}{V}}}\times \left\langle a_{\mathbf {k} \lambda }(0)a_{\mathbf {k'} \lambda '}^{\dagger }(0)\right\rangle \\&={\frac {1}{4\pi }}\sum _{\mathbf {k} \lambda }\left({\frac {2\pi \hbar \omega _{k}}{V}}\right)\\&=\int _{0}^{\infty }dw\,\rho _{0}(\omega )\end{aligned}}$$

The important point of this is that the zero-point field energy H_F does not affect the Heisenberg equation for a_kλ since it is a c-number or constant (i.e. an ordinary number rather than an operator) and commutes with a_kλ. We can therefore drop the zero-point field energy from the Hamiltonian, as is usually done. But the zero-point field re-emerges as the homogeneous solution for the field equation. A charged particle in the vacuum will therefore always see a zero-point field of infinite density. This is the origin of one of the infinities of quantum electrodynamics, and it cannot be eliminated by the trivial expedient dropping of the term Σ_kλ ħω_k/2 in the field Hamiltonian.

The free field is in fact necessary for the formal consistency of the theory. In particular, it is necessary for the preservation of the commutation relations, which is required by the unitary of time evolution in quantum theory:

$${\begin{aligned}\left[z(t),p_{z}(t)\right]&=\left[U^{\dagger }(t)z(0)U(t),U^{\dagger }(t)p_{z}(0)U(t)\right]\\&=U^{\dagger }(t)\left[z(0),p_{z}(0)\right]U(t)\\&=i\hbar U^{\dagger }(t)U(t)\\&=i\hbar \end{aligned}}$$

We can calculate [z(t),p_z(t)] from the formal solution of the operator equation of motion

$$\mathbf {\ddot {x}} +\omega _{0}^{2}\mathbf {x} -\tau \mathbf {\overset {...}{x}} ={\frac {e}{m}}\mathbf {E} _{0}(t)$$

Using the fact that

$$\left[a_{\mathbf {k} \lambda }(0),a_{\mathbf {k'} \lambda '}^{\dagger }(0)\right]=\delta _{\mathbf {kk'} }^{3},\delta _{\lambda \lambda '}$$

and that equal-time particle and field operators commute, we obtain:

$${\begin{aligned}[z(t),p_{z}(t)]&=\left[z(t),m{\dot {z}}(t)\right]+\left[z(t),{\frac {e}{c}}A_{z}(t)\right]\\&=\left[z(t),m{\dot {z}}(t)\right]\\&=\left({\frac {i\hbar e^{2}}{2\pi ^{2}mc^{3}}}\right)\left({\frac {8\pi }{3}}\right)\int _{0}^{\infty }{\frac {d\omega \,\omega ^{4}}{\left(\omega ^{2}-\omega _{0}^{2}\right)^{2}+\tau ^{2}\omega ^{6}}}\end{aligned}}$$

For the dipole oscillator under consideration it can be assumed that the radiative damping rate is small compared with the natural oscillation frequency, i.e., τω₀ ≪ 1. Then the integrand above is sharply peaked at ω = ω₀ and:

$${\begin{aligned}\left[z(t),p_{z}(t)\right]&\approx {\frac {2i\hbar e^{2}}{3\pi mc^{3}}}\omega _{0}^{3}\int _{-\infty }^{\infty }{\frac {dx}{x^{2}+\tau ^{2}\omega _{0}^{6}}}\\&=\left({\frac {2i\hbar e^{2}\omega _{0}^{3}}{3\pi mc^{3}}}\right)\left({\frac {\pi }{\tau \omega _{0}^{3}}}\right)\\&=i\hbar \end{aligned}}$$

the necessity of the vacuum field can also be appreciated by making the small damping approximation in

$${\begin{aligned}&\mathbf {\ddot {x}} +\omega _{0}^{2}\mathbf {x} -\tau \mathbf {\overset {...}{x}} ={\frac {e}{m}}\mathbf {E} _{0}(t)\\&\mathbf {\ddot {x}} \approx -\omega _{0}^{2}\mathbf {x} (t)&&\mathbf {\overset {...}{x}} \approx -\omega _{0}^{2}\mathbf {\dot {x}} \end{aligned}}$$

and

$$\mathbf {\ddot {x}} +\tau \omega _{0}^{2}\mathbf {\dot {x}} +\omega _{0}^{2}\mathbf {x} \approx {\frac {e}{m}}\mathbf {E} _{0}(t)$$

Without the free field E₀(t) in this equation the operator x(t) would be exponentially dampened, and commutators like [z(t),p_z(t)] would approach zero for t ≫ 1/τω²
₀. With the vacuum field included, however, the commutator is iħ at all times, as required by unitarity, and as we have just shown. A similar result is easily worked out for the case of a free particle instead of a dipole oscillator.

What we have here is an example of a "fluctuation-dissipation elation". Generally speaking if a system is coupled to a bath that can take energy from the system in an effectively irreversible way, then the bath must also cause fluctuations. The fluctuations and the dissipation go hand in hand we cannot have one without the other. In the current example the coupling of a dipole oscillator to the electromagnetic field has a dissipative component, in the form of the zero-point (vacuum) field; given the existence of radiation reaction, the vacuum field must also exist in order to preserve the canonical commutation rule and all it entails.

The spectral density of the vacuum field is fixed by the form of the radiation reaction field, or vice versa: because the radiation reaction field varies with the third derivative of x, the spectral energy density of the vacuum field must be proportional to the third power of ω in order for [z(t),p_z(t)] to hold. In the case of a dissipative force proportional to ẋ, by contrast, the fluctuation force must be proportional to $\omega$ in order to maintain the canonical commutation relation. This relation between the form of the dissipation and the spectral density of the fluctuation is the essence of the fluctuation-dissipation theorem.

The fact that the canonical commutation relation for a harmonic oscillator coupled to the vacuum field is preserved implies that the zero-point energy of the oscillator is preserved. it is easy to show that after a few damping times the zero-point motion of the oscillator is in fact sustained by the driving zero-point field.

Quantum chromodynamic vacuum

Main article: QCD vacuum

The QCD vacuum is the vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by a non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter. In technical terms, gluons are vector gauge bosons that mediate strong interactions of quarks in quantum chromodynamics (QCD). Gluons themselves carry the color charge of the strong interaction. This is unlike the photon, which mediates the electromagnetic interaction but lacks an electric charge. Gluons therefore participate in the strong interaction in addition to mediating it, making QCD significantly harder to analyze than QED (quantum electrodynamics) as it deals with nonlinear equations to characterize such interactions.

Higgs field

Main article: Higgs mechanism

The potential for the Higgs field, plotted as function of ϕ⁰ and ϕ³. It has a Mexican-hat or champagne-bottle profile at the ground.

The Standard Model hypothesises a field called the Higgs field (symbol: ϕ), which has the unusual property of a non-zero amplitude in its ground state (zero-point) energy after renormalization; i.e., a non-zero vacuum expectation value. It can have this effect because of its unusual "Mexican hat" shaped potential whose lowest "point" is not at its "centre". Below a certain extremely high energy level the existence of this non-zero vacuum expectation spontaneously breaks electroweak gauge symmetry which in turn gives rise to the Higgs mechanism and triggers the acquisition of mass by those particles interacting with the field. The Higgs mechanism occurs whenever a charged field has a vacuum expectation value. This effect occurs because scalar field components of the Higgs field are "absorbed" by the massive bosons as degrees of freedom, and couple to the fermions via Yukawa coupling, thereby producing the expected mass terms. The expectation value of ϕ⁰ in the ground state (the vacuum expectation value or VEV) is then ⟨ϕ⁰⟩ = v/√2, where v = |μ|/√λ. The measured value of this parameter is approximately 246 GeV/c². It has units of mass, and is the only free parameter of the Standard Model that is not a dimensionless number.

The Higgs mechanism is a type of superconductivity which occurs in the vacuum. It occurs when all of space is filled with a sea of particles which are charged and thus the field has a nonzero vacuum expectation value. Interaction with the vacuum energy filling the space prevents certain forces from propagating over long distances (as it does in a superconducting medium; e.g., in the Ginzburg–Landau theory).

Experimental observations

Zero-point energy has many observed physical consequences. It is important to note that zero-point energy is not merely an artifact of mathematical formalism that can, for instance, be dropped from a Hamiltonian by redefining the zero of energy, or by arguing that it is a constant and therefore has no effect on Heisenberg equations of motion without latter consequence. Indeed, such treatment could create a problem at a deeper, as of yet undiscovered, theory. For instance, in general relativity the zero of energy (i.e. the energy density of the vacuum) contributes to a cosmological constant of the type introduced by Einstein in order to obtain static solutions to his field equations. The zero-point energy density of the vacuum, due to all quantum fields, is extremely large, even when we cut off the largest allowable frequencies based on plausible physical arguments. It implies a cosmological constant larger than the limits imposed by observation by about 120 orders of magnitude. This "cosmological constant problem" remains one of the greatest unsolved mysteries of physics.

Casimir effect

Main article: Casimir effect

Casimir forces on parallel plates

A phenomenon that is commonly presented as evidence for the existence of zero-point energy in vacuum is the Casimir effect, proposed in 1948 by Dutch physicist Hendrik Casimir, who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. The vacuum energy contains contributions from all wavelengths, except those excluded by the spacing between plates. As the plates draw together, more wavelengths are excluded and the vacuum energy decreases. The decrease in energy means there must be a force doing work on the plates as they move.

Early experimental tests from the 1950s onwards gave positive results showing the force was real, but other external factors could not be ruled out as the primary cause, with the range of experimental error sometimes being nearly 100%. That changed in 1997 with Lamoreaux conclusively showing that the Casimir force was real. Results have been repeatedly replicated since then.

In 2009, Munday et al. published experimental proof that (as predicted in 1961) the Casimir force could also be repulsive as well as being attractive. Repulsive Casimir forces could allow quantum levitation of objects in a fluid and lead to a new class of switchable nanoscale devices with ultra-low static friction.

An interesting hypothetical side effect of the Casimir effect is the Scharnhorst effect, a hypothetical phenomenon in which light signals travel slightly faster than c between two closely spaced conducting plates.

Lamb shift

Main article: Lamb shift

Fine structure of energy levels in hydrogen – relativistic corrections to the Bohr model

The quantum fluctuations of the electromagnetic field have important physical consequences. In addition to the Casimir effect, they also lead to a splitting between the two energy levels ²S_1/2 and ²P_1/2 (in term symbol notation) of the hydrogen atom which was not predicted by the Dirac equation, according to which these states should have the same energy. Charged particles can interact with the fluctuations of the quantized vacuum field, leading to slight shifts in energy; this effect is called the Lamb shift. The shift of about 4.38×10⁻⁶ eV is roughly 10⁻⁷ of the difference between the energies of the 1s and 2s levels, and amounts to 1,058 MHz in frequency units. A small part of this shift (27 MHz ≈ 3%) arises not from fluctuations of the electromagnetic field, but from fluctuations of the electron–positron field. The creation of (virtual) electron–positron pairs has the effect of screening the Coulomb field and acts as a vacuum dielectric constant. This effect is much more important in muonic atoms.

Fine-structure constant

Main article: Fine-structure constant

Taking ħ (the Planck constant divided by 2π), c (the speed of light), and e² = q²
_e/4πε₀ (the electromagnetic coupling constant i.e. a measure of the strength of the electromagnetic force (where q_e is the absolute value of the electronic charge and $\varepsilon _{0}$ is the vacuum permittivity)) we can form a dimensionless quantity called the fine-structure constant:

$$\alpha ={\frac {e^{2}}{\hbar c}}={\frac {q_{e}^{2}}{4\pi \varepsilon _{0}\hbar c}}\approx {\frac {1}{137}}$$

The fine-structure constant is the coupling constant of quantum electrodynamics (QED) determining the strength of the interaction between electrons and photons. It turns out that the fine-structure constant is not really a constant at all owing to the zero-point energy fluctuations of the electron-positron field. The quantum fluctuations caused by zero-point energy have the effect of screening electric charges: owing to (virtual) electron-positron pair production, the charge of the particle measured far from the particle is far smaller than the charge measured when close to it.

The Heisenberg inequality where ħ = h/2π, and Δ_x, Δ_p are the standard deviations of position and momentum states that:

$$\Delta _{x}\Delta _{p}\geq {\frac {1}{2}}\hbar$$

It means that a short distance implies large momentum and therefore high energy i.e. particles of high energy must be used to explore short distances. QED concludes that the fine-structure constant is an increasing function of energy. It has been shown that at energies of the order of the Z⁰ boson rest energy, m_zc² ≈ 90 GeV, that:

$$\alpha \approx {\frac {1}{129}}$$

rather than the low-energy α ≈ 1/137. The renormalization procedure of eliminating zero-point energy infinities allows the choice of an arbitrary energy (or distance) scale for defining α. All in all, α depends on the energy scale characteristic of the process under study, and also on details of the renormalization procedure. The energy dependence of α has been observed for several years now in precision experiment in high-energy physics.

Vacuum birefringence

Main articles: Lorentz-violating electrodynamics and Euler–Heisenberg Lagrangian

Light coming from the surface of a strongly magnetic neutron star (left) becomes linearly polarised as it travels through the vacuum.

In the presence of strong electrostatic fields it is predicted that virtual particles become separated from the vacuum state and form real matter. The fact that electromagnetic radiation can be transformed into matter and vice versa leads to fundamentally new features in quantum electrodynamics. One of the most important consequences is that, even in the vacuum, the Maxwell equations have to be exchanged by more complicated formulas. In general, it will be not possible to separate processes in the vacuum from the processes involving matter since electromagnetic fields can create matter if the field fluctuations are strong enough. This leads to highly complex nonlinear interaction - gravity will have an effect on the light at the same time the light has an effect on gravity. These effects were first predicted by Werner Heisenberg and Hans Heinrich Euler in 1936 and independently the same year by Victor Weisskopf who stated: "The physical properties of the vacuum originate in the "zero-point energy" of matter, which also depends on absent particles through the external field strengths and therefore contributes an additional term to the purely Maxwellian field energy". Thus strong magnetic fields vary the energy contained in the vacuum. The scale above which the electromagnetic field is expected to become nonlinear is known as the Schwinger limit. At this point the vacuum has all the properties of a birefringent medium, thus in principle a rotation of the polarization frame (the Faraday effect) can be observed in empty space.

Wide field view of the neutron star RX J1856.5-3754

Both Einstein's theory of special and general relativity state that light should pass freely through a vacuum without being altered, a principle known as Lorentz invariance. Yet, in theory, large nonlinear self-interaction of light due to quantum fluctuations should lead to this principle being measurably violated if the interactions are strong enough. Nearly all theories of quantum gravity predict that Lorentz invariance is not an exact symmetry of nature. It is predicted the speed at which light travels through the vacuum depends on its direction, polarization and the local strength of the magnetic field. There have been a number of inconclusive results which claim to show evidence of a Lorentz violation by finding a rotation of the polarization plane of light coming from distant galaxies. The first concrete evidence for vacuum birefringence was published in 2017 when a team of astronomers looked at the light coming from the star RX J1856.5-3754, the closest discovered neutron star to Earth.

Roberto Mignani at the National Institute for Astrophysics in Milan who led the team of astronomers has commented that "When Einstein came up with the theory of general relativity 100 years ago, he had no idea that it would be used for navigational systems. The consequences of this discovery probably will also have to be realised on a longer timescale." The team found that visible light from the star had undergone linear polarisation of around 16%. If the birefringence had been caused by light passing through interstellar gas or plasma, the effect should have been no more than 1%. Definitive proof would require repeating the observation at other wavelengths and on other neutron stars. At X-ray wavelengths the polarization from the quantum fluctuations should be near 100%. Although no telescope currently exists that can make such measurements, there are several proposed X-ray telescopes that may soon be able to verify the result conclusively such as China's Hard X-ray Modulation Telescope (HXMT) and NASA's Imaging X-ray Polarimetry Explorer (IXPE).

Speculated involvement in other phenomena

Dark energy

Main article: Dark energy

Unsolved problem in physics:

Why does the large zero-point energy of the vacuum not cause a large cosmological constant? What cancels it out?

(more unsolved problems in physics)

In the late 1990s it was discovered that very distant supernovae were dimmer than expected suggesting that the universe's expansion was accelerating rather than slowing down. This revived discussion that Einstein's cosmological constant, long disregarded by physicists as being equal to zero, was in fact some small positive value. This would indicate empty space exerted some form of negative pressure or energy.

There is no natural candidate for what might cause what has been called dark energy but the current best guess is that it is the zero-point energy of the vacuum, but this guess is known to be off by 120 orders of magnitude.

The European Space Agency's Euclid telescope, launched on 1 July 2023, will map galaxies up to 10 billion light years away. By seeing how dark energy influences their arrangement and shape, the mission will allow scientists to see if the strength of dark energy has changed. If dark energy is found to vary throughout time it would indicate it is due to quintessence, where observed acceleration is due to the energy of a scalar field, rather than the cosmological constant. No evidence of quintessence is yet available, but it has not been ruled out either. It generally predicts a slightly slower acceleration of the expansion of the universe than the cosmological constant. Some scientists think that the best evidence for quintessence would come from violations of Einstein's equivalence principle and variation of the fundamental constants in space or time. Scalar fields are predicted by the Standard Model of particle physics and string theory, but an analogous problem to the cosmological constant problem (or the problem of constructing models of cosmological inflation) occurs: renormalization theory predicts that scalar fields should acquire large masses again due to zero-point energy.

Cosmic inflation

Main article: Inflation (cosmology)

Unsolved problem in physics:

Why does the observable universe have more matter than antimatter?

(more unsolved problems in physics)

Cosmic inflation is phase of accelerated cosmic expansion just after the Big Bang. It explains the origin of the large-scale structure of the cosmos. It is believed quantum vacuum fluctuations caused by zero-point energy arising in the microscopic inflationary period, later became magnified to a cosmic size, becoming the gravitational seeds for galaxies and structure in the Universe (see galaxy formation and evolution and structure formation). Many physicists also believe that inflation explains why the Universe appears to be the same in all directions (isotropic), why the cosmic microwave background radiation is distributed evenly, why the Universe is flat, and why no magnetic monopoles have been observed.

The mechanism for inflation is unclear, it is similar in effect to dark energy but is a far more energetic and short lived process. As with dark energy the best explanation is some form of vacuum energy arising from quantum fluctuations. It may be that inflation caused baryogenesis, the hypothetical physical processes that produced an asymmetry (imbalance) between baryons and antibaryons produced in the very early universe, but this is far from certain.

Cosmology

Paul S. Wesson examined the cosmological implications of assuming that zero-point energy is real. Among numerous difficulties, general relativity requires that such energy not gravitate, so it cannot be similar to electromagnetic radiation.

Alternative theories

There has been a long debate over the question of whether zero-point fluctuations of quantized vacuum fields are "real" i.e. do they have physical effects that cannot be interpreted by an equally valid alternative theory? Schwinger, in particular, attempted to formulate QED without reference to zero-point fluctuations via his "source theory". From such an approach it is possible to derive the Casimir Effect without reference to a fluctuating field. Such a derivation was first given by Schwinger (1975) for a scalar field, and then generalized to the electromagnetic case by Schwinger, DeRaad, and Milton (1978). in which they state "the vacuum is regarded as truly a state with all physical properties equal to zero". Jaffe (2005) has highlighted a similar approach in deriving the Casimir effect stating "the concept of zero-point fluctuations is a heuristic and calculational aid in the description of the Casimir effect, but not a necessity in QED."

Milonni has shown the necessity of the vacuum field for the formal consistency of QED. Modern physics does not know any better way to construct gauge-invariant, renormalizable theories than with zero-point energy and they would seem to be a necessity for any attempt at a unified theory.Nevertheless, as pointed out by Jaffe, "noknown phenomenon, including the Casimir effect, demonstrates that zero point energies are “real”"

Chaotic and emergent phenomena

See also: Chaos theory, Emergence, and Self-organization

The mathematical models used in classical electromagnetism, quantum electrodynamics (QED) and the Standard Model all view the electromagnetic vacuum as a linear system with no overall observable consequence. For example, in the case of the Casimir effect, Lamb shift, and so on these phenomena can be explained by alternative mechanisms other than action of the vacuum by arbitrary changes to the normal ordering of field operators. See the alternative theories section. This is a consequence of viewing electromagnetism as a U(1) gauge theory, which topologically does not allow the complex interaction of a field with and on itself. In higher symmetry groups and in reality, the vacuum is not a calm, randomly fluctuating, largely immaterial and passive substance, but at times can be viewed as a turbulent virtual plasma that can have complex vortices (i.e. solitons vis-à-vis particles), entangled states and a rich nonlinear structure. There are many observed nonlinear physical electromagnetic phenomena such as Aharonov–Bohm (AB) and Altshuler–Aronov–Spivak (AAS) effects, Berry, Aharonov–Anandan, Pancharatnam and Chiao–Wu phase rotation effects, Josephson effect, Quantum Hall effect, the De Haas–Van Alphen effect, the Sagnac effect and many other physically observable phenomena which would indicate that the electromagnetic potential field has real physical meaning rather than being a mathematical artifact and therefore an all encompassing theory would not confine electromagnetism as a local force as is currently done, but as a SU(2) gauge theory or higher geometry. Higher symmetries allow for nonlinear, aperiodic behaviour which manifest as a variety of complex non-equilibrium phenomena that do not arise in the linearised U(1) theory, such as multiple stable states, symmetry breaking, chaos and emergence.

What are called Maxwell's equations today, are in fact a simplified version of the original equations reformulated by Heaviside, FitzGerald, Lodge and Hertz. The original equations used Hamilton's more expressive quaternion notation, a kind of Clifford algebra, which fully subsumes the standard Maxwell vectorial equations largely used today. In the late 1880s there was a debate over the relative merits of vector analysis and quaternions. According to Heaviside the electromagnetic potential field was purely metaphysical, an arbitrary mathematical fiction, that needed to be "murdered". It was concluded that there was no need for the greater physical insights provided by the quaternions if the theory was purely local in nature. Local vector analysis has become the dominant way of using Maxwell's equations ever since. However, this strictly vectorial approach has led to a restrictive topological understanding in some areas of electromagnetism, for example, a full understanding of the energy transfer dynamics in Tesla's oscillator-shuttle-circuit can only be achieved in quaternionic algebra or higher SU(2) symmetries. It has often been argued that quaternions are not compatible with special relativity, but multiple papers have shown ways of incorporating relativity.

A good example of nonlinear electromagnetics is in high energy dense plasmas, where vortical phenomena occur which seemingly violate the second law of thermodynamics by increasing the energy gradient within the electromagnetic field and violate Maxwell's laws by creating ion currents which capture and concentrate their own and surrounding magnetic fields. In particular Lorentz force law, which elaborates Maxwell's equations is violated by these force free vortices. These apparent violations are due to the fact that the traditional conservation laws in classical and quantum electrodynamics (QED) only display linear U(1) symmetry (in particular, by the extended Noether theorem, conservation laws such as the laws of thermodynamics need not always apply to dissipative systems, which are expressed in gauges of higher symmetry). The second law of thermodynamics states that in a closed linear system entropy flow can only be positive (or exactly zero at the end of a cycle). However, negative entropy (i.e. increased order, structure or self-organisation) can spontaneously appear in an open nonlinear thermodynamic system that is far from equilibrium, so long as this emergent order accelerates the overall flow of entropy in the total system. The 1977 Nobel Prize in Chemistry was awarded to thermodynamicist Ilya Prigogine for his theory of dissipative systems that described this notion. Prigogine described the principle as "order through fluctuations" or "order out of chaos". It has been argued by some that all emergent order in the universe from galaxies, solar systems, planets, weather, complex chemistry, evolutionary biology to even consciousness, technology and civilizations are themselves examples of thermodynamic dissipative systems; nature having naturally selected these structures to accelerate entropy flow within the universe to an ever-increasing degree. For example, it has been estimated that human body is 10,000 times more effective at dissipating energy per unit of mass than the sun.

One may query what this has to do with zero-point energy. Given the complex and adaptive behaviour that arises from nonlinear systems considerable attention in recent years has gone into studying a new class of phase transitions which occur at absolute zero temperature. These are quantum phase transitions which are driven by EM field fluctuations as a consequence of zero-point energy. A good example of a spontaneous phase transition that are attributed to zero-point fluctuations can be found in superconductors. Superconductivity is one of the best known empirically quantified macroscopic electromagnetic phenomena whose basis is recognised to be quantum mechanical in origin. The behaviour of the electric and magnetic fields under superconductivity is governed by the London equations. However, it has been questioned in a series of journal articles whether the quantum mechanically canonised London equations can be given a purely classical derivation. Bostick, for instance, has claimed to show that the London equations do indeed have a classical origin that applies to superconductors and to some collisionless plasmas as well. In particular it has been asserted that the Beltrami vortices in the plasma focus display the same paired flux-tube morphology as Type II superconductors. Others have also pointed out this connection, Fröhlich has shown that the hydrodynamic equations of compressible fluids, together with the London equations, lead to a macroscopic parameter ($\mu$ = electric charge density / mass density), without involving either quantum phase factors or the Planck constant. In essence, it has been asserted that Beltrami plasma vortex structures are able to at least simulate the morphology of Type I and Type II superconductors. This occurs because the "organised" dissipative energy of the vortex configuration comprising the ions and electrons far exceeds the "disorganised" dissipative random thermal energy. The transition from disorganised fluctuations to organised helical structures is a phase transition involving a change in the condensate's energy (i.e. the ground state or zero-point energy) but without any associated rise in temperature. This is an example of zero-point energy having multiple stable states (see Quantum phase transition, Quantum critical point, Topological degeneracy, Topological order) and where the overall system structure is independent of a reductionist or deterministic view, that "classical" macroscopic order can also causally affect quantum phenomena. Furthermore, the pair production of Beltrami vortices has been compared to the morphology of pair production of virtual particles in the vacuum.

Artist's conception of the expansion of the universe. On the left, the dramatic expansion occurs in the inflationary epoch.

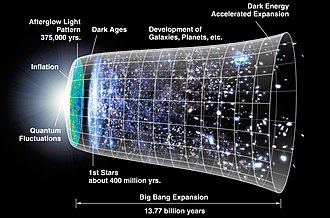
The idea that the vacuum energy can have multiple stable energy states is a leading hypothesis for the cause of cosmic inflation. In fact, it has been argued that these early vacuum fluctuations led to the expansion of the universe and in turn have guaranteed the non-equilibrium conditions necessary to drive order from chaos, as without such expansion the universe would have reached thermal equilibrium and no complexity could have existed. With the continued accelerated expansion of the universe, the cosmos generates an energy gradient that increases the "free energy" (i.e. the available, usable or potential energy for useful work) which the universe is able to use to create ever more complex forms of order. The only reason Earth's environment does not decay into an equilibrium state is that it receives a daily dose of sunshine and that, in turn, is due to the sun "polluting" interstellar space with entropy. The sun's fusion power is only possible due to the gravitational disequilibrium of matter that arose from cosmic expansion. In this essence, the vacuum energy can be viewed as the key cause of the structure throughout the universe. That humanity might alter the morphology of the vacuum energy to create an energy gradient for useful work is the subject of much controversy.

Purported applications

Physicists overwhelmingly reject any possibility that the zero-point energy field can be exploited to obtain useful energy (work) or uncompensated momentum; such efforts are seen as tantamount to perpetual motion machines.

Nevertheless, the allure of free energy has motivated such research, usually falling in the category of fringe science. As long ago as 1889 (before quantum theory or discovery of the zero point energy) Nikola Tesla proposed that useful energy could be obtained from free space, or what was assumed at that time to be an all-pervasive aether. Others have since claimed to exploit zero-point or vacuum energy with a large amount of pseudoscientific literature causing ridicule around the subject. Despite rejection by the scientific community, harnessing zero-point energy remains an interest of research, particularly in the US where it has attracted the attention of major aerospace/defence contractors and the U.S. Department of Defense as well as in China, Germany, Russia and Brazil.

Casimir batteries and engines

A common assumption is that the Casimir force is of little practical use; the argument is made that the only way to actually gain energy from the two plates is to allow them to come together (getting them apart again would then require more energy), and therefore it is a one-use-only tiny force in nature. In 1984 Robert Forward published work showing how a "vacuum-fluctuation battery" could be constructed; the battery can be recharged by making the electrical forces slightly stronger than the Casimir force to reexpand the plates.

In 1999, Pinto, a former scientist at NASA's Jet Propulsion Laboratory at Caltech in Pasadena, published in Physical Review his thought experiment (Gedankenexperiment) for a "Casimir engine". The paper showed that continuous positive net exchange of energy from the Casimir effect was possible, even stating in the abstract "In the event of no other alternative explanations, one should conclude that major technological advances in the area of endless, by-product free-energy production could be achieved."

Garret Moddel at University of Colorado has highlighted that he believes such devices hinge on the assumption that the Casimir force is a nonconservative force, he argues that there is sufficient evidence (e.g. analysis by Scandurra (2001)) to say that the Casimir effect is a conservative force and therefore even though such an engine can exploit the Casimir force for useful work it cannot produce more output energy than has been input into the system.

In 2008, DARPA solicited research proposals in the area of Casimir Effect Enhancement (CEE). The goal of the program is to develop new methods to control and manipulate attractive and repulsive forces at surfaces based on engineering of the Casimir force.

A 2008 patent by Haisch and Moddel details a device that is able to extract power from zero-point fluctuations using a gas that circulates through a Casimir cavity. A published test of this concept by Moddel was performed in 2012 and seemed to give excess energy that could not be attributed to another source. However it has not been conclusively shown to be from zero-point energy and the theory requires further investigation.

Single heat baths

In 1951 Callen and Welton proved the quantum fluctuation-dissipation theorem (FDT) which was originally formulated in classical form by Nyquist (1928) as an explanation for observed Johnson noise in electric circuits. Fluctuation-dissipation theorem showed that when something dissipates energy, in an effectively irreversible way, a connected heat bath must also fluctuate. The fluctuations and the dissipation go hand in hand; it is impossible to have one without the other. The implication of FDT being that the vacuum could be treated as a heat bath coupled to a dissipative force and as such energy could, in part, be extracted from the vacuum for potentially useful work. Such a theory has met with resistance: Macdonald (1962) and Harris (1971) claimed that extracting power from the zero-point energy to be impossible, so FDT could not be true. Grau and Kleen (1982) and Kleen (1986), argued that the Johnson noise of a resistor connected to an antenna must satisfy Planck's thermal radiation formula, thus the noise must be zero at zero temperature and FDT must be invalid. Kiss (1988) pointed out that the existence of the zero-point term may indicate that there is a renormalization problem—i.e., a mathematical artifact—producing an unphysical term that is not actually present in measurements (in analogy with renormalization problems of ground states in quantum electrodynamics). Later, Abbott et al. (1996) arrived at a different but unclear conclusion that "zero-point energy is infinite thus it should be renormalized but not the 'zero-point fluctuations'". Despite such criticism, FDT has been shown to be true experimentally under certain quantum, non-classical conditions. Zero-point fluctuations can, and do, contribute towards systems which dissipate energy. A paper by Armen Allahverdyan and Theo Nieuwenhuizen in 2000 showed the feasibility of extracting zero-point energy for useful work from a single bath, without contradicting the laws of thermodynamics, by exploiting certain quantum mechanical properties.

There have been a growing number of papers showing that in some instances the classical laws of thermodynamics, such as limits on the Carnot efficiency, can be violated by exploiting negative entropy of quantum fluctuations.

Despite efforts to reconcile quantum mechanics and thermodynamics over the years, their compatibility is still an open fundamental problem. The full extent that quantum properties can alter classical thermodynamic bounds is unknown

Space travel and gravitational shielding

The use of zero-point energy for space travel is speculative and does not form part of the mainstream scientific consensus. A complete quantum theory of gravitation (that would deal with the role of quantum phenomena like zero-point energy) does not yet exist. Speculative papers explaining a relationship between zero-point energy and gravitational shielding effects have been proposed, but the interaction (if any) is not yet fully understood. According to the general theory of relativity, rotating matter can generate a new force of nature, known as the gravitomagnetic interaction, whose intensity is proportional to the rate of spin. In certain conditions the gravitomagnetic field can be repulsive. In neutrons stars for example it can produce a gravitational analogue of the Meissner effect, but the force produced in such an example is theorized to be exceedingly weak.

In 1963 Robert Forward, a physicist and aerospace engineer at Hughes Research Laboratories, published a paper showing how within the framework of general relativity "anti-gravitational" effects might be achieved. Since all atoms have spin, gravitational permeability may be able to differ from material to material. A strong toroidal gravitational field that acts against the force of gravity could be generated by materials that have nonlinear properties that enhance time-varying gravitational fields. Such an effect would be analogous to the nonlinear electromagnetic permeability of iron making it an effective core (i.e. the doughnut of iron) in a transformer, whose properties are dependent on magnetic permeability. In 1966 Dewitt was first to identify the significance of gravitational effects in superconductors. Dewitt demonstrated that a magnetic-type gravitational field must result in the presence of fluxoid quantization. In 1983, Dewitt's work was substantially expanded by Ross.

From 1971 to 1974 Henry William Wallace, a scientist at GE Aerospace was issued with three patents. Wallace used Dewitt's theory to develop an experimental apparatus for generating and detecting a secondary gravitational field, which he named the kinemassic field (now better known as the gravitomagnetic field). In his three patents, Wallace describes three different methods used for detection of the gravitomagnetic field – change in the motion of a body on a pivot, detection of a transverse voltage in a semiconductor crystal, and a change in the specific heat of a crystal material having spin-aligned nuclei. There are no publicly available independent tests verifying Wallace's devices. Such an effect if any would be small. Referring to Wallace's patents, a New Scientist article in 1980 stated "Although the Wallace patents were initially ignored as cranky, observers believe that his invention is now under serious but secret investigation by the military authorities in the USA. The military may now regret that the patents have already been granted and so are available for anyone to read." A further reference to Wallace's patents occur in an electric propulsion study prepared for the Astronautics Laboratory at Edwards Air Force Base which states: "The patents are written in a very believable style which include part numbers, sources for some components, and diagrams of data. Attempts were made to contact Wallace using patent addresses and other sources but he was not located nor is there a trace of what became of his work. The concept can be somewhat justified on general relativistic grounds since rotating frames of time varying fields are expected to emit gravitational waves."

In 1986 the U.S. Air Force's then Rocket Propulsion Laboratory (RPL) at Edwards Air Force Base solicited "Non Conventional Propulsion Concepts" under a small business research and innovation program. One of the six areas of interest was "Esoteric energy sources for propulsion, including the quantum dynamic energy of vacuum space..." In the same year BAE Systems launched "Project Greenglow" to provide a "focus for research into novel propulsion systems and the means to power them".

In 1988 Kip Thorne et al. published work showing how traversable wormholes can exist in spacetime only if they are threaded by quantum fields generated by some form of exotic matter that has negative energy. In 1993 Scharnhorst and Barton showed that the speed of a photon will be increased if it travels between two Casimir plates, an example of negative energy. In the most general sense, the exotic matter needed to create wormholes would share the repulsive properties of the inflationary energy, dark energy or zero-point radiation of the vacuum. Building on the work of Thorne, in 1994 Miguel Alcubierre proposed a method for changing the geometry of space by creating a wave that would cause the fabric of space ahead of a spacecraft to contract and the space behind it to expand (see Alcubierre drive). The ship would then ride this wave inside a region of flat space, known as a warp bubble and would not move within this bubble but instead be carried along as the region itself moves due to the actions of the drive.

In 1992 Evgeny Podkletnov published a heavily debated journal article claiming a specific type of rotating superconductor could shield gravitational force. Independently of this, from 1991 to 1993 Ning Li and Douglas Torr published a number of articles about gravitational effects in superconductors. One finding they derived is the source of gravitomagnetic flux in a type II superconductor material is due to spin alignment of the lattice ions. Quoting from their third paper: "It is shown that the coherent alignment of lattice ion spins will generate a detectable gravitomagnetic field, and in the presence of a time-dependent applied magnetic vector potential field, a detectable gravitoelectric field." The claimed size of the generated force has been disputed by some but defended by others. In 1997 Li published a paper attempting to replicate Podkletnov's results and showed the effect was very small, if it existed at all. Li is reported to have left the University of Alabama in 1999 to found the company AC Gravity LLC. AC Gravity was awarded a U.S. DOD grant for $448,970 in 2001 to continue anti-gravity research. The grant period ended in 2002 but no results from this research were ever made public.

In 2002 Phantom Works, Boeing's advanced research and development facility in Seattle, approached Evgeny Podkletnov directly. Phantom Works was blocked by Russian technology transfer controls. At this time Lieutenant General George Muellner, the outgoing head of the Boeing Phantom Works, confirmed that attempts by Boeing to work with Podkletnov had been blocked by Moscow, also commenting that "The physical principles – and Podkletnov's device is not the only one – appear to be valid... There is basic science there. They're not breaking the laws of physics. The issue is whether the science can be engineered into something workable"

Froning and Roach (2002) put forward a paper that builds on the work of Puthoff, Haisch and Alcubierre. They used fluid dynamic simulations to model the interaction of a vehicle (like that proposed by Alcubierre) with the zero-point field. Vacuum field perturbations are simulated by fluid field perturbations and the aerodynamic resistance of viscous drag exerted on the interior of the vehicle is compared to the Lorentz force exerted by the zero-point field (a Casimir-like force is exerted on the exterior by unbalanced zero-point radiation pressures). They find that the optimized negative energy required for an Alcubierre drive is where it is a saucer-shaped vehicle with toroidal electromagnetic fields. The EM fields distort the vacuum field perturbations surrounding the craft sufficiently to affect the permeability and permittivity of space.

In 2009 Giorgio Fontana and Bernd Binder presented a new method to potentially extract the Zero-point energy of the electromagnetic field and nuclear forces in the form of gravitational waves. In the spheron model of the nucleus, proposed by the two times Nobel laureate Linus Pauling, dineutrons are among the components of this structure. Similarly to a dumbbell put in a suitable rotational state, but with nuclear mass density, dineutrons are nearly ideal sources of gravitational waves at X-ray and gamma-ray frequencies. The dynamical interplay, mediated by nuclear forces, between the electrically neutral dineutrons and the electrically charged core nucleus is the fundamental mechanism by which nuclear vibrations can be converted to a rotational state of dineutrons with emission of gravitational waves. Gravity and gravitational waves are well described by General Relativity, that is not a quantum theory, this implies that there is no Zero-point energy for gravity in this theory, therefore dineutrons will emit gravitational waves like any other known source of gravitational waves. In Fontana and Binder paper, nuclear species with dynamical instabilites, related to the Zero-point energy of the electromagnetic field and nuclear forces, and possessing dineutrons, will emit gravitational waves. In experimental physics this approach is still unexplored.

In 2014 NASA's Eagleworks Laboratories announced that they had successfully validated the use of a Quantum Vacuum Plasma Thruster which makes use of the Casimir effect for propulsion. In 2016 a scientific paper by the team of NASA scientists passed peer review for the first time. The paper suggests that the zero-point field acts as pilot-wave and that the thrust may be due to particles pushing off the quantum vacuum. While peer review doesn't guarantee that a finding or observation is valid, it does indicate that independent scientists looked over the experimental setup, results, and interpretation and that they could not find any obvious errors in the methodology and that they found the results reasonable. In the paper, the authors identify and discuss nine potential sources of experimental errors, including rogue air currents, leaky electromagnetic radiation, and magnetic interactions. Not all of them could be completely ruled out, and further peer-reviewed experimentation is needed in order to rule these potential errors out.

Zero-point energy in fiction

The concept of Zero-point energy used as an energy source has been an element used in science fiction and related media.

See also

• Casimir effect
• Ground state
• Lamb shift
• QED vacuum
• QCD vacuum
• Quantum fluctuation
• Quantum foam
• Scalar field
• Time crystal
• Topological order
• Unruh effect
• Vacuum energy
• Vacuum expectation value
• Vacuum state
• Virtual particle

References

Статьи в прессе

• Баттерсби, С. (20 ноября 2008 г.). «Подтверждено: материя — это всего лишь колебания вакуума» . Новый учёный . Архивировано из оригинала 27 мая 2017 года.
• Беннетт, Дж. (30 ноября 2016 г.). «Ученые ловят «виртуальные частицы», которые появляются и исчезают» . Популярная механика . Архивировано из оригинала 29 мая 2017 года.
• Чо, А. (1 октября 2015 г.). «Физики наблюдают странные квантовые флуктуации в пустом пространстве — возможно» . Наука . дои : 10.1126/science.aad4655 . Архивировано из оригинала 27 мая 2017 года.
• Чо, А. (30 ноября 2016 г.). «Астрономы заметили признаки странного квантового искажения в космосе» . Наука . дои : 10.1126/science.aal0437 . Архивировано из оригинала 29 мая 2017 года.
• Чой, CQ (12 февраля 2013 г.). «Что-то из ничего? Вакуум может давать вспышки света» . Научный американец . Архивировано из оригинала 30 мая 2017 года.
• Чоун, М. (7 апреля 1990 г.). «Наука: могут ли фотоны путешествовать быстрее света?» . Новый учёный . Архивировано из оригинала 30 мая 2017 года.
• Кук, Н. (29 июля 2002 г.). «Антигравитационное движение выходит «из шкафа» » . Еженедельник защиты Джейн . Лондон. Архивировано из оригинала 2 августа 2002 года.
• Крейн, Л. (30 ноября 2016 г.). «Квантовые частицы искажают свет нейтронной звезды» . Новый учёный . Архивировано из оригинала 29 мая 2017 года.
• Дэвис, PCW (22 сентября 1994 г.). «Теория инерции: волшебный круговой перекресток. Пол Дэвис о значении принципа Маха» . Хранитель . Архивировано из оригинала 17 января 1999 года.
• Дэвис, PCW (19 ноября 2011 г.). «Из эфира: меняющееся лицо вакуума». Новый учёный . Том. 212, нет. 2839. стр. 50–52. Бибкод : 2011NewSc.212Q..50D . дои : 10.1016/S0262-4079(11)62858-3 .
• Лучентини, Дж. (28 сентября 2000 г.). «Веские последствия: НАСА финансирует спорный гравитационный щит» . SPACE.com . Архивировано из оригинала 9 ноября 2000 года.
• Мэтьюз, Р. (25 февраля 1995 г.). «Ничто лучше вакуума» . Новый учёный . Том. 145, нет. 1966. стр. 30–33. Архивировано из оригинала 13 апреля 2016 года . Через Институт Калфизики .
• О'Кэрролл, Э. (25 марта 2013 г.). «Учёные ничего не исследуют, а что-то находят» . Христианский научный монитор . Архивировано из оригинала 31 марта 2013 года.
• Пилкингтон, М. (17 июля 2003 г.). «Энергия нулевой точки» . Хранитель . Архивировано из оригинала 7 февраля 2017 года.
• Пауэлл, CS (1994). «Невыносимая легкость: новая теория может объяснить, почему объекты имеют тенденцию оставаться на месте». Научный американец . 270 (5): 30–31. doi : 10.1038/scientificamerican0594-27 .
• Скотт, Всемирный банк (март 2004 г.). «К звездам» (PDF) . Неделя авиации и космических технологий . стр. 50–53. Архивировано из оригинала (PDF) 26 февраля 2017 года . Проверено 25 октября 2016 г.
• Сигел, Э. (22 сентября 2016 г.). «Что такое физика ничего?» . Форбс . Архивировано из оригинала 27 мая 2017 года.
• Сига, Д. (28 сентября 2005 г.). «Вакуумная энергия: что-то даром?» . Новый учёный . Архивировано из оригинала 27 мая 2017 года.
• Уолл, М. (27 марта 2014 г.). «Происходит ли темная энергия из «квантового вакуума?» " . SPACE.com . Архивировано из оригинала 29 марта 2014 года.

Библиография

• Эбботт, Д.; Дэвис, БР; Филлипс, Нью-Джерси; Эшрагян, К. (1996). «Простой вывод формулы теплового шума с использованием преобразований Фурье с ограниченным окном и других загадок». Транзакции IEEE по образованию . 39 (1): 1–13. Бибкод : 1996ITEdu..39....1A . CiteSeerX   10.1.1.129.5792 . дои : 10.1109/13.485226 .
• Бартон, Г.; Шарнхорст, К. (1993). «КЭД между параллельными зеркалами: световые сигналы быстрее, чем c , или усиливаются вакуумом». Журнал физики A: Математический и общий . 26 (8): 2037–2046. Бибкод : 1993JPhA...26.2037B . дои : 10.1088/0305-4470/26/8/024 . ISSN   0305-4470 .
• Баттерсби, Стивен (2016). «Темная энергия: Глядя во тьму» . Природа . 537 (7622): 201–204. Бибкод : 2016Natur.537S.201B . дои : 10.1038/537S201a . ПМИД   27681049 . S2CID   4398296 .
• Бордаг, М; Климчицкая Г.Л.; Мохидин, У.; Мостепаненко, В. М. (2009). Достижения в области эффекта Казимира . Оксфорд: Издательство Оксфордского университета. ISBN  978-0-19-923874-3 . LCCN   2009279136 . OCLC   319209483 .
• Бостик, Вашингтон; Прайор, В.; Грюнбергер, Л.; Эммерт, Г. (1966). «Парное рождение плазменных вихрей». Физика жидкостей . 9 (10): 2078. Бибкод : 1966PhFl....9.2078B . дои : 10.1063/1.1761572 .
• Бресси, Г.; Каруньо, Г.; Онофрио, Р.; Руозо, Г. (2002). «Измерение силы Казимира между параллельными металлическими поверхностями». Письма о физических отзывах . 88 (4): 041804. arXiv : quant-ph/0203002 . Бибкод : 2002PhRvL..88d1804B . doi : 10.1103/PhysRevLett.88.041804 . ПМИД   11801108 . S2CID   43354557 .
• Капассо, Ф.; Мандей, JN; Яннуцци, Д.; Чан, Х.Б. (2007). «Силы Казимира и квантовые электродинамические моменты: физика и наномеханика» (PDF) . Журнал IEEE по избранным темам квантовой электроники . 13 (2): 400–414. Бибкод : 2007IJSTQ..13..400C . дои : 10.1109/JSTQE.2007.893082 . S2CID   32996610 .
• Кэрролл, С.М. ; Филд, Великобритания (1997). «Есть ли доказательства космической анизотропии в поляризации далеких радиоисточников?» (PDF) . Письма о физических отзывах . 79 (13): 2394–2397. arXiv : astro-ph/9704263 . Бибкод : 1997PhRvL..79.2394C . doi : 10.1103/PhysRevLett.79.2394 . ISSN   0031-9007 . S2CID   13943605 .
• Чан, Х.Б.; Аксюк, В.А.; Клейман, Р.Н.; Бишоп, диджей; Капассо, Ф. (2001). «Квантово-механическое приведение в действие микроэлектромеханических систем силой Казимира» (PDF) . Наука . 291 (5510): 1941–1944. Бибкод : 2001Sci...291.1941C . дои : 10.1126/science.1057984 . ПМИД   11239149 . S2CID   17072357 .
• Конлон, Т.Э. (2011). Думая ни о чем: Отто фон Герике и Магдебургские эксперименты с вакуумом . Сан-Франциско: Сент-Остин Пресс. ISBN  978-1-4478-3916-3 . OCLC   840927124 .
• Корреа, Луизиана; Палао, Япония; Алонсо, Д.; Адессо, Г. (2014). «Абсорбционные холодильники с квантовым усилением» . Научные отчеты . 4 (3949): 3949. arXiv : 1308.4174 . Бибкод : 2014NatSR...4E3949C . дои : 10.1038/srep03949 . ПМЦ   3912482 . ПМИД   24492860 .
• Дэвис, PCW (1985). Суперсила: В поисках Великой Единой Теории Природы . Нью-Йорк: Саймон и Шустер. ISBN  978-0-671-47685-4 . LCCN   84005473 . OCLC   12397205 .
• Декка, РС; Лопес, Д.; Фишбах, Э.; Краузе, Германия (2003). «Измерение силы Казимира между разнородными металлами» . Письма о физических отзывах . 91 (5): 050402. arXiv : quant-ph/0306136 . Бибкод : 2003PhRvL..91e0402D . doi : 10.1103/PhysRevLett.91.050402 . ПМИД   12906584 . S2CID   20243276 .
• Дирак, Поль AM (1927). «Квантовая теория испускания и поглощения излучения» (PDF) . Учеб. Р. Сок. А. ​ 114 (767): 243–265. Бибкод : 1927RSPSA.114..243D . дои : 10.1098/rspa.1927.0039 . Архивировано из оригинала (PDF) 25 октября 2016 года . Проверено 17 октября 2016 г.
• Дрексхаге, К.Х. (1970). «Мономолекулярные слои и свет». Научный американец . 222 (3): 108–119. Бибкод : 1970SciAm.222c.108D . doi : 10.1038/scientificamerican0370-108 .
• Дрексхаге, К.Х. (1974). «IV Взаимодействие света с мономолекулярными слоями красителя». В Вольф, Э. (ред.). Прогресс в оптике . Том. 12. С. 163–232. дои : 10.1016/S0079-6638(08)70266-X . ISBN  978-0-444-10571-4 .
• Данн, Г.В. (2012). «Эффективные действия Гейзенберга-Эйлера: 75 лет спустя». Международный журнал современной физики А. 27 (15): 1260004. arXiv : 1202.1557 . Бибкод : 2012IJMPA..2760004D . дои : 10.1142/S0217751X12600044 . ISSN   0217-751X . S2CID   119258601 .
• Эйнштейн, А. (1995). Кляйн, Мартин Дж.; Кокс, Эй Джей; Ренн, Юрген; Шульманн, Роберт (ред.). Сборник статей Альберта Эйнштейна Том. 4 Швейцарские годы: сочинения, 1912–1914 гг . Принстон: Издательство Принстонского университета. ISBN  978-0-691-03705-9 . OCLC   929349643 .
• Эйнштейн, А. (1993). Кляйн, Мартин Дж.; Кокс, Эй Джей; Шульманн, Роберт (ред.). Сборник статей Альберта Эйнштейна Том. 5 Швейцарские годы: переписка, 1902–1914 гг . Принстон: Издательство Принстонского университета. ISBN  978-0-691-03322-8 . OCLC   921496342 .
• Гой, П.; Раймонд, Дж. М.; Гросс, М.; Гарош, С. (1983). «Наблюдение спонтанной эмиссии одного атома, усиленной резонатором». Письма о физических отзывах . 50 (24): 1903–1906. Бибкод : 1983PhRvL..50.1903G . doi : 10.1103/PhysRevLett.50.1903 .
• Грейнер, В.; Мюллер, Б.; Рафельски, Дж. (2012). Квантовая электродинамика сильных полей: с введением в современную релятивистскую квантовую механику . Спрингер. дои : 10.1007/978-3-642-82272-8 . ISBN  978-0-387-13404-8 . LCCN   84026824 . ОСЛК   317097176 .
• Хайш, Б.; Руэда, А.; Путхофф, HE (1994). «Инерция как сила Лоренца в нулевом поле» (PDF) . Физический обзор А. 49 (2): 678–694. Бибкод : 1994PhRvA..49..678H . дои : 10.1103/PhysRevA.49.678 . ПМИД   9910287 . Архивировано из оригинала (PDF) 31 июля 2018 года . Проверено 17 октября 2016 г.
• Гейзенберг, В.; Эйлер, Х. (1936). «Выводы из теории позитрона Дирака». Журнал физики . 98 (11–12): 714–732. arXiv : физика/0605038 . Бибкод : 1936ZPhy...98..714H . дои : 10.1007/BF01343663 . ISSN   1434-6001 . S2CID   120354480 .
• Хейл, Дж.С.; Шавив, Нью-Джерси (2000). «Эволюция поляризации в сильных магнитных полях». Ежемесячные уведомления Королевского астрономического общества . 311 (3): 555–564. arXiv : astro-ph/9909339 . Бибкод : 2000MNRAS.311..555H . дои : 10.1046/j.1365-8711.2000.03076.x . ISSN   0035-8711 . S2CID   11717019 .
• Ицыксон, К.; Зубер, Ж.-Б. (1980). Квантовая теория поля (изд. 2005 г.). Минеола, Нью-Йорк: Dover Publications. ISBN  978-0486445687 . LCCN   2005053026 . OCLC   61200849 .
• Костелецкий, В. Алан; Мьюз, М. (2009). «Электродинамика с операторами произвольной размерности, нарушающими Лоренц». Физический обзор D . 80 (1): 015020.arXiv : 0905.0031 . Бибкод : 2009PhRvD..80a5020K . doi : 10.1103/PhysRevD.80.015020 . ISSN   1550-7998 . S2CID   119241509 .
• Костелецкий, В. Алан; Мьюз, М. (2013). «Ограничения на нарушения теории относительности из-за гамма-всплесков». Письма о физических отзывах . 110 (20): 201601. arXiv : 1301.5367 . Бибкод : 2013PhRvL.110t1601K . doi : 10.1103/PhysRevLett.110.201601 . ISSN   0031-9007 . ПМИД   25167393 . S2CID   8579347 .
• Ковитт, Марк (1994). «Гравитомагнетизм и магнитная проницаемость в сверхпроводниках». Физический обзор B . 49 (1): 704–708. Бибкод : 1994PhRvB..49..704K . дои : 10.1103/PhysRevB.49.704 . ПМИД   10009347 .
• Краг, Х. (2002). Квантовые поколения: история физики двадцатого века . Издательство Принстонского университета. ISBN  978-0-691-09552-3 . OCLC   248763258 .
• Краг, Х. (2012). «Прелюдии к темной энергии: энергия нулевой точки и предположения о вакууме». Архив истории точных наук . 66 (3): 199–240. arXiv : 1111.4623 . дои : 10.1007/s00407-011-0092-3 . ISSN   0003-9519 . S2CID   118593162 .
• Краг, HS; Овердуин, Дж. М. (2014). Вес вакуума: научная история темной энергии . Нью-Йорк: Спрингер. ISBN  978-3-642-55089-8 . LCCN   2014938218 . OCLC   884863929 .
• Кун, Т. (1978). Теория черного тела и квантовый разрыв, 1894–1912 гг . Нью-Йорк: Издательство Оксфордского университета. ISBN  978-0-19-502383-1 . LCCN   77019022 . OCLC   803538583 .
• Ле Беллак, М. (2006). Квантовая физика (изд. 2012 г.). Издательство Кембриджского университета. ISBN  978-1-107-60276-2 . OCLC   957316740 .
• Лейхс, Г.; Санчес-Сото, LL (2013). «Правило сумм для заряженных элементарных частиц». Европейский физический журнал Д. 67 (3): 57. arXiv : 1301.3923 . Бибкод : 2013EPJD...67...57L . дои : 10.1140/epjd/e2013-30577-8 . ISSN   1434-6060 . S2CID   118643015 .
• Лаудон, Р. (2000). Квантовая теория света (3-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN  978-0198501770 . LCCN   2001265846 . ОСЛК   44602993 .
• Мэтьюз, Р. (1994). «Инерция: выдерживает ли пустое пространство сопротивление?» . Наука . 263 (5147): 612–613. Бибкод : 1994Sci...263..612M . дои : 10.1126/science.263.5147.612 . ISSN   0036-8075 . JSTOR   2883066 . PMID   17747645 – через Институт Калфизики.
• Миньяни, РП; Теста, В.; Гонсалес Канюлеф, Д.; Таверна, Р.; Туролла, Р.; Зейн, С.; Ву, К. (2017). «Доказательства вакуумного двойного лучепреломления, полученные в результате первого измерения оптической поляриметрии изолированной нейтронной звезды RX J1856.5-3754» (PDF) . Ежемесячные уведомления Королевского астрономического общества . 465 (1): 492–500. arXiv : 1610.08323 . Бибкод : 2017MNRAS.465..492M . дои : 10.1093/mnras/stw2798 . ISSN   0035-8711 . S2CID   38736536 .
• Милонни, PW (1981). «Радиационная реакция и нерелятивистская теория электрона». Буквы по физике А. 82 (5): 225–226. Бибкод : 1981PhLA...82..225M . дои : 10.1016/0375-9601(81)90191-2 .
• Милонни, PW (1983). «Зависит ли электромагнитная масса электрона от того, где он находится?». Международный журнал теоретической физики . 22 (4): 323–328. Бибкод : 1983IJTP...22..323M . дои : 10.1007/BF02082897 . S2CID   119991060 .
• Милонни, PW (1994). Квантовый вакуум: введение в квантовую электродинамику . Бостон: Академическая пресса. ISBN  978-0124980808 . LCCN   93029780 . OCLC   422797902 .
• Милонни, PW (2009). «Энергия нулевой точки» . В Гринбергере, Д.; Хентшель, К.; Вайнерт, Ф. (ред.). Сборник квантовой физики: концепции, эксперименты, история и философия . Берлин, Гейдельберг: Springer. стр. 864–866. arXiv : 0811.2516 . дои : 10.1007/978-3-540-70626-7 . ISBN  9783540706229 . LCCN   2008942038 . OCLC   297803628 .
• Пиблз, PJE ; Ратра, Бхарат (2003). «Космологическая константа и темная энергия». Обзоры современной физики . 75 (2): 559–606. arXiv : astro-ph/0207347 . Бибкод : 2003РвМП...75..559П . дои : 10.1103/RevModPhys.75.559 . ISSN   0034-6861 . S2CID   118961123 .
• Пенроуз, Роджер (2004). Дорога к реальности (8-е изд.). Нью-Йорк: Альфред А. Кнопф. ISBN  978-0-679-45443-4 . OCLC   474890537 .
• Перлмуттер, С .; Альдеринг; Гольдхабер; Кноп; Ньюджент; Кастро; Деустуа; Фаббро; Губар; и др. (1999). «Измерения Ω и Λ по 42 сверхновым с высоким красным смещением». Астрофизический журнал . 517 (2): 565–86. arXiv : astro-ph/9812133 . Бибкод : 1999ApJ...517..565P . дои : 10.1086/307221 . S2CID   118910636 .
• Пескин, Мэн; Шредер, Д.В. (1995). Введение в квантовую теорию поля . Аддисон-Уэсли. ISBN  978-0-201-50397-5 . OCLC   635667163 .
• Пинто, Ф. (1999). «Цикл двигателя вакуумного преобразователя энергии с оптическим управлением». Физический обзор B . 60 (21): 14740. Бибкод : 1999PhRvB..6014740P . дои : 10.1103/PhysRevB.60.14740 .
• Планк, М. (1900). «К теории закона распределения энергии в нормальном спектре». Переговоры Немецкого физического общества . 2 :237-245.
• Планк, М. (1911). «Новая радиационная гипотеза». Переговоры Немецкого физического общества . 13 :138-148.
• Планк, М. (1912а). «Об обосновании закона черного излучения» . Анналы физики . 37 (4): 642–656. Бибкод : 1912АнП...342..642П . дои : 10.1002/andp.19123420403 .
• Планк, М. (1912b). «Закон черного излучения и гипотеза элементарных величин действия». В Ланжевене, П .; Сольвей, Э .; де Бройль, М. (ред.). Теория излучения и квантов . Париж: Готье-Виллар. стр. 93 –114. LCCN   unk84021539 . OCLC   5894537227 .
• Планк, М. (1913). Лекции по теории теплового излучения . Лейпциг: Дж. А. Барт. OCLC   924400975 .
• Планк, М. (1958). Физические трактаты и лекции. Том 2 . Брауншвейг: Vieweg & Son. LCCN59047616   . OCLC   603096370 .
• Мощность, Э.А. (1964). Введение в квантовую электродинамику . Лондон: Лонгманс. LCCN   65020006 . OCLC   490279969 .
• Рид, Д. (1995). «Фундаментальная электродинамика и векторные поля Бельтрами» . В Барретте, Теренс Уильям; Граймс, Дейл М. (ред.). Расширенный электромагнетизм: основы, теория и приложения . Сингапур: World Scientific. стр. 217–249. ISBN  978-981-02-2095-2 .
• Рис, Мартин , изд. (2012). Вселенная . Нью-Йорк: Паб DK. ISBN  978-0-7566-9841-6 . LCCN   2011277855 . OCLC   851193468 .
• Риек, К.; Селецкий, Д.В.; Москаленко А.С.; Шмидт, Дж. Ф.; Крауспе, П.; Эккарт, С.; Эггерт, С.; Буркард, Г.; Лейтенсторфер, А. (2015). «Прямой отбор проб флуктуаций вакуума электрического поля» (PDF) . Наука . 350 (6259): 420–423. Бибкод : 2015Sci...350..420R . дои : 10.1126/science.aac9788 . ISSN   0036-8075 . ПМИД   26429882 . S2CID   40368170 .
• Рисс, АГ ; Филиппенко; Чаллис; Клоккьятти; Диркс; Гарнавич; Гиллиленд; Хоган; Джа; и др. (1998). «Наблюдательные данные сверхновых об ускоряющейся Вселенной и космологической постоянной». Астрономический журнал . 116 (3): 1009–38. arXiv : astro-ph/9805201 . Бибкод : 1998AJ....116.1009R . дои : 10.1086/300499 . S2CID   15640044 .
• Росснагель, Дж.; Абах, О.; Шмидт-Калер, Ф.; Сингер, К.; Лутц, Э. (2014). «Наномасштабная тепловая машина за пределом Карно». Письма о физических отзывах . 112 (3): 030602. arXiv : 1308.5935 . Бибкод : 2014PhRvL.112c0602R . doi : 10.1103/PhysRevLett.112.030602 . ПМИД   24484127 . S2CID   1826585 .
• Раг, ЮВ; Зинкернагель, Х. (2002). «Квантовый вакуум и проблема космологической постоянной». Исследования по истории и философии науки. Часть B: Исследования по истории и философии современной физики . 33 (4): 663–705. arXiv : hep-th/0012253 . Бибкод : 2002ШПМП..33..663Р . дои : 10.1016/S1355-2198(02)00033-3 . ISSN   1355-2198 . S2CID   9007190 .
• Сондерс, Саймон ; Браун, Харви Р. , ред. (1991). Философия вакуума . Оксфорд: Издательство Оксфордского университета. ISBN  978-0198244493 . LCCN   90048906 . OCLC   774073198 .
• Швингер, Дж. (1998a). Частицы, источники и поля: Том I. Ридинг, Массачусетс: Расширенная книжная программа, Perseus Books. ISBN  978-0-7382-0053-8 . LCCN   98087896 . OCLC   40544377 .
• Швингер, Дж. (1998b). Частицы, источники и поля: Том II . Ридинг, Массачусетс: Расширенная книжная программа, Perseus Books. ISBN  978-0-7382-0054-5 . LCCN   98087896 . OCLC   40544377 .
• Швингер, Дж. (1998c). Частицы, источники и поля: Том III . Ридинг, Массачусетс: Расширенная книжная программа, Perseus Books. ISBN  978-0-7382-0055-2 . LCCN   98087896 . OCLC   40544377 .
• Скиама, Д.В. (1991). «Физическое значение вакуумного состояния квантового поля». В Сондерсе, Саймон ; Браун, Харви Р. (ред.). Философия вакуума . Оксфорд: Издательство Оксфордского университета. ISBN  978-0198244493 . LCCN   90048906 . OCLC   774073198 .
• Скотт, Олвин (2006). Энциклопедия нелинейной науки . Рутледж. ISBN  978-1-57958-385-9 . OCLC   937249213 .
• Скалли, Миссури; Зубайри, М.С. (1997). Квантовая оптика . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-43595-6 . OCLC   444869786 .
• Скалли, Миссури (2001). «Извлечение работы из одиночной тепловой ванны посредством квантовой негэнтропии». Письма о физических отзывах . 87 (22). 220601. Бибкод : 2001PhRvL..87v0601S . doi : 10.1103/PhysRevLett.87.220601 . ПМИД   11736390 .
• Скалли, Миссури; Зубайри, М.С.; Агарвал, Г.С.; Вальтер, Х. (2003). «Извлечение работы из одной тепловой ванны посредством исчезновения квантовой когерентности» . Наука . 299 (5608): 862–863. Бибкод : 2003Sci...299..862S . дои : 10.1126/science.1078955 . ПМИД   12511655 . S2CID   120884236 .
• Урбан, М.; Кушо, Ф.; Саразин, X.; Джаннати-Атай, А. (2013). «Квантовый вакуум как происхождение скорости света». Европейский физический журнал Д. 67 (3): 58. arXiv : 1302,6165 . Бибкод : 2013EPJD...67...58U . дои : 10.1140/epjd/e2013-30578-7 . ISSN   1434-6060 . S2CID   15753833 .
• Вайнберг, С. (1989). «Проблема космологической постоянной» (PDF) . Обзоры современной физики . 61 (1): 1–23. Бибкод : 1989РвМП...61....1Вт . дои : 10.1103/RevModPhys.61.1 . hdl : 2152/61094 . ISSN   0034-6861 . S2CID   122259372 .
• Вайнберг, С. (2015). Лекции по квантовой механике (2-е изд.). Кембридж: Издательство Кембриджского университета. ISBN  978-1-107-11166-0 . LCCN   2015021123 . OCLC   910664598 .
• Вайскопф, В. (1936). «К электродинамике вакуума на основе квантовой теории электрона» ( PDF) . Kongelige Danske Videnskabernes Selskab, Mathematisk-fysiske Meddelelse . 24 (6): 3–39.
• Уайт, Х.; Марш, П.; Лоуренс, Дж.; Вера, Дж.; Сильвестр, А.; Брэди, Д.; Бейли, П. (2016). «Измерение импульсной тяги закрытого радиочастотного резонатора в вакууме». Журнал движения и мощности . 33 (4): 830–841. дои : 10.2514/1.B36120 . hdl : 2060/20170000277 . S2CID   126303009 .
• Уайт, Х.; Марш, П.; Уильямс, Н.; О'Нил, В. (5 декабря 2011 г.). Eagleworks Laboratories: Исследования в области перспективной физики двигательных установок (PDF) . Совместное совещание JANNAF; 5–9 декабря 2011 г.; Хантсвилл, Алабама . Проверено 24 октября 2016 г.
• Уилсон, CM; Йоханссон, Г.; Пуркабирян, А.; Симоен, М.; Йоханссон-младший; Долг, Т.; Нори, Ф.; Дельсинг, П. (2011). «Наблюдение динамического эффекта Казимира в сверхпроводящей цепи». Природа . 479 (7373): 376–379. arXiv : 1105.4714 . Бибкод : 2011Natur.479..376W . дои : 10.1038/nature10561 . ISSN   0028-0836 . ПМИД   22094697 . S2CID   219735 .
• Вудс, Р.К. (2005). «Управление гравитационными волнами для приложений связи с использованием сверхпроводников». Физика C: Сверхпроводимость . 433 (1–2): 101–107. Бибкод : 2005PhyC..433..101W . дои : 10.1016/j.physc.2005.10.003 .
• Вудс, Колорадо; Кук, СГ; Хельме, Дж.; Колдуэлл, CH (2001). «Гравитационная модификация высокотемпературными сверхпроводниками». 37-я совместная конференция и выставка AIAA по двигательной технике . дои : 10.2514/6.2001-3363 .

Дальнейшее чтение

Статьи в прессе

• Брамфилд, Г. (3 июня 2011 г.). «Движущиеся зеркала создают свет из ничего» . Природа . дои : 10.1038/news.2011.346 .
• Брукс, М. (16 ноября 2011 г.). «Свет, вырванный из пустого пространства» . Новый учёный . Архивировано из оригинала 30 мая 2017 года.
• Картлидж, Э. (17 ноября 2011 г.). «Как превратить тьму в свет» . Мир физики . Институт физики. Архивировано из оригинала 30 мая 2017 года.
• Маркус, А. (12 октября 2009 г.). «Исследования в вакууме: DARPA пытается использовать неуловимый эффект Казимира для революционной технологии» . Научный американец . Архивировано из оригинала 2 марта 2015 года.
• Мэтьюз, Р.; Образец, И. (1 сентября 1996 г.). « Антигравитационное устройство дает науке новый импульс» . «Санди телеграф» . Архивировано из оригинала 6 марта 2003 года.
• Скиама, DW (2 февраля 1978 г.). «Трансмогрифицированный эфир» . Новый учёный . Том. 77, нет. 1088. стр. 298–300 – через Google Книги.
• Йирка, Б. (2 октября 2015 г.). «Исследовательская группа утверждает, что непосредственно измерила колебания вакуума электрического поля» . Физика.орг . Архивировано из оригинала 27 мая 2017 года.

Журнальные статьи

• Бойер, TH (1970). «Квантовая энергия нулевой точки и силы дальнего действия». Анналы физики . 56 (2): 474–503. Бибкод : 1970AnPhy..56..474B . дои : 10.1016/0003-4916(70)90027-8 . ISSN   0003-4916 .
• Булсара, Арканзас; Гамайтони, Л. (1996). «Настройка на шум» (PDF) . Физика сегодня . 49 (3): 39–45. Бибкод : 1996PhT....49c..39B . дои : 10.1063/1.881491 . ISSN   0031-9228 . Архивировано из оригинала (PDF) 12 июля 2018 года . Проверено 31 мая 2017 г.
• Лахтеенмаки, П.; Параоану, Г.С.; Хассель, Дж.; Хаконен, П.Дж. (2013). «Динамический эффект Казимира в метаматериале Джозефсона» . Труды Национальной академии наук . 110 (11): 4234–4238. arXiv : 1111.5608 . Бибкод : 2013PNAS..110.4234L . дои : 10.1073/pnas.1212705110 . ISSN   0027-8424 . S2CID   10972781 .

Книги

• Бейзер, А. (2003). Концепции современной физики (6-е изд.). Бостон: МакГроу-Хилл. ISBN  978-0072448481 . LCCN   2001044743 . OCLC   48965418 .
• Хайтлер, В. (1984). Квантовая теория радиации (переиздание 1954 г., 3-е изд.). Нью-Йорк: Dover Publications. ISBN  978-0486645582 . LCCN   83005201 . OCLC   924845769 .
• Рафельски, Дж .; Мюллер, Б. (1985). Структурированный вакуум: ни о чем не думая (PDF) . Х. Дойч: Тун. ISBN  978-3871448898 . LCCN   86175968 . OCLC   946050522 .

Внешние ссылки

• Нима Аркани-Хамед о проблеме вакуумной энергии и темной энергии .
• Стивен Вайнберг о проблеме космологической постоянной .