Частота Раби

Частота Раби — это частота, с которой амплитуды вероятности двух уровней атомной энергии колеблются в колеблющемся электромагнитном поле. Он пропорционален переходному дипольному моменту двух уровней и амплитуде ( не напряженности ) электромагнитного поля . Перенос населения между уровнями такой двухуровневой системы, освещенной светом, точно резонансным с разницей в энергии между двумя уровнями, будет происходить на частоте Раби; когда падающий свет отстроен от этой разности энергий (отстроен от резонанса), тогда перенос населенности происходит на обобщенной частоте Раби . Частота Раби — это квазиклассическая концепция, поскольку она рассматривает атом как объект с квантованными уровнями энергии , а электромагнитное поле — как непрерывную волну.

В контексте эксперимента по ядерному магнитному резонансу частота Раби представляет собой частоту нутации вектора чистой ядерной намагниченности образца относительно радиочастотного поля. (Обратите внимание, что это отличается от ларморовской частоты , которая характеризует прецессию поперечной ядерной намагниченности вокруг статического магнитного поля.)

Вывод

Рассмотрим два собственных состояния энергии квантовой системы с гамильтонианом ${\hat {H}}_{0}$ (например, это может быть гамильтониан частицы в ${\frac {1}{r}}$ потенциал, такой как атом водорода или атомы щелочи):

$${\begin{aligned}\psi _{1}(\mathbf {r} ,t)&=e^{-i\omega _{1}t}|1\rangle \\\psi _{2}(\mathbf {r} ,t)&=e^{-i\omega _{2}t}|2\rangle \end{aligned}}$$

Мы хотим рассмотреть зависящий от времени гамильтониан

$${\hat {\mathcal {H}}}={\hat {H}}_{0}+{\hat {V}}(t)$$

где ${\hat {V}}(t)=e\mathbf {r} \cdot \mathbf {E} _{0}\cos(\omega t)$ – потенциал электромагнитного поля. Рассматривая потенциал как возмущение , мы можем ожидать, что собственные состояния возмущенного гамильтониана будут некоторой смесью собственных состояний исходного гамильтониана с коэффициентами, зависящими от времени:

$$\Psi (\mathbf {r} ,t)=c_{1}(t)e^{-i\omega _{1}t}|1\rangle +c_{2}(t)e^{-i\omega _{2}t}|2\rangle$$

Подключая это к зависящему от времени уравнению Шредингера

$$i\hbar {\frac {\partial \Psi (\mathbf {r} ,t)}{\partial t}}={\hat {\mathcal {H}}}\Psi (\mathbf {r} ,t)$$

беря внутренний продукт с каждым из $e^{i\omega _{1}t}\langle 1|$ и $e^{i\omega _{2}t}\langle 2|$и используя условие ортогональности собственных состояний $\langle i|j\rangle =\delta _{i,j}$, придем к двум уравнениям с коэффициентами $c_{1}(t)$ и $c_{2}(t)$:

$${\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {c_{1}(t)\cos(\omega t)}{\hbar }}\langle 1|e\mathbf {r} \cdot \mathbf {E} _{0}|1\rangle +{\frac {e^{i\omega _{0}t}c_{2}(t)\cos(\omega t)}{\hbar }}\langle 1|e\mathbf {r} \cdot \mathbf {E} _{0}|2\rangle \\i{\dot {c}}_{2}(t)&={\frac {c_{2}(t)\cos(\omega t)}{\hbar }}\langle 2|e\mathbf {r} \cdot \mathbf {E} _{0}|2\rangle +{\frac {e^{-i\omega _{0}t}c_{1}(t)\cos(\omega t)}{\hbar }}\langle 2|e\mathbf {r} \cdot \mathbf {E} _{0}|1\rangle \end{aligned}}$$

где $\omega _{0}=\omega _{1}-\omega _{2}$. Два члена в скобках представляют собой дипольные матричные элементы, нанесенные точками на вектор поляризации электромагнитного поля. При рассмотрении сферически-симметричных пространственных собственных функций $|i\rangle$ потенциала атома водорода диагональные матричные элементы обращаются к нулю, оставляя нас с

$${\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {c_{2}(t)\cos(\omega t)}{\hbar }}\langle 1|e\mathbf {r} \cdot \mathbf {E} _{0}|2\rangle e^{i\omega _{0}t}\\i{\dot {c}}_{2}(t)&={\frac {c_{1}(t)\cos(\omega t)}{\hbar }}\langle 2|e\mathbf {r} \cdot \mathbf {E} _{0}|1\rangle e^{-i\omega _{0}t}\end{aligned}}$$

или

$${\begin{aligned}i{\dot {c}}_{1}(t)&=\Omega c_{2}(t)\cos(\omega t)e^{i\omega _{0}t}\\i{\dot {c}}_{2}(t)&=\Omega ^{*}c_{1}(t)\cos(\omega t)e^{-i\omega _{0}t}\end{aligned}}$$

Здесь $\Omega :=\Omega _{1,2}$, где $\Omega _{i,j}={\frac {\langle i|e\mathbf {r} \cdot \mathbf {E} _{0}|j\rangle }{\hbar }}$ — частота Раби.

Интуиция

В числителе стоит дипольный момент перехода для $i\to j$ переход, квадрат амплитуды которого представляет силу взаимодействия между электромагнитным полем и атомом, и $\mathbf {E} _{0}={\hat {\epsilon }}E_{0}$ – векторная электрического поля амплитуда , включающая поляризацию . Числитель имеет размерность энергии, поэтому деление на $\hbar$ дает угловую частоту .

По аналогии с классическим диполем ясно, что атом с большим дипольным моментом будет более подвержен возмущению электрическим полем. Скалярное произведение включает в себя коэффициент $\cos \theta$, где $\theta$ — угол между поляризацией света и дипольным моментом перехода. Когда они параллельны, взаимодействие наиболее сильное, когда они перпендикулярны, взаимодействия нет вообще.

Если переписать найденные выше дифференциальные уравнения:

$${\begin{aligned}i{\dot {c}}_{1}(t)=\Omega c_{2}(t)\cos(\omega t)e^{i\omega _{0}t}&\to {\frac {\Omega c_{2}}{2}}(e^{i(\omega -\omega _{0})t}+e^{-i(\omega +\omega _{0})t})\\i{\dot {c}}_{2}(t)=\Omega ^{*}c_{1}(t)\cos(\omega t)e^{-i\omega _{0}t}&\to {\frac {\Omega ^{*}c_{1}}{2}}(e^{i(\omega +\omega _{0})t}+e^{-i(\omega -\omega _{0})t})\end{aligned}}$$

и применить приближение вращающейся волны , которое предполагает, что $\omega +\omega _{0}>>\omega -\omega _{0}$, так что мы можем отбросить высокочастотные осциллирующие члены, мы имеем

$${\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {\Omega c_{2}}{2}}e^{i\delta t}\\i{\dot {c}}_{2}(t)&={\frac {\Omega ^{*}c_{1}}{2}}e^{-i\delta t}\end{aligned}}$$

где $\delta =\omega -\omega _{0}$ называется расстройкой между лазерной и атомной частотами.

Мы можем решить эти уравнения, предполагая, что в момент времени $t=0$ атом находится внутри $|1\rangle$ (т.е. $c_{1}(0)=1$), чтобы найти

$$|c_{2}(t)|^{2}={\frac {\Omega ^{2}\sin ^{2}{\bigg (}{\frac {{\sqrt {\Omega ^{2}+\delta ^{2}}}t}{2}}{\bigg )}}{\Omega ^{2}+\delta ^{2}}}$$

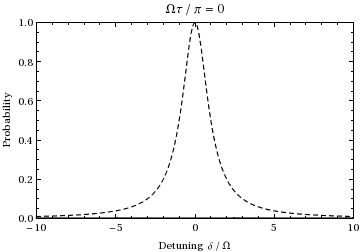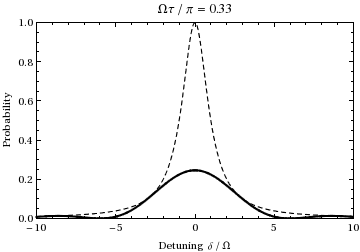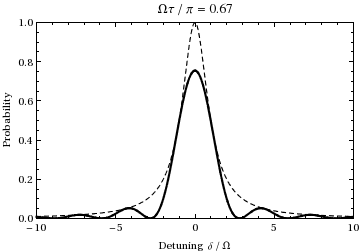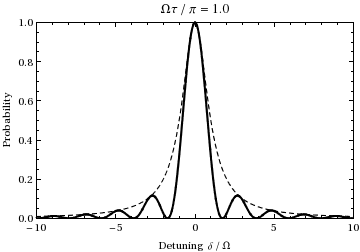
Это вероятность как функция расстройки и времени населения состояния. $|2\rangle$. График как функция расстройки и изменения времени от 0 до $t={\frac {\pi }{\Omega }}$ дает:

Мы видим это для $\delta =0$ население будет колебаться между двумя состояниями на частоте Раби.

Обобщенная частота Раби

Количество ${\sqrt {\Omega ^{2}+\delta ^{2}}}$ обычно называют «обобщенной частотой Раби». Для случаев, когда $\delta \neq 0$, провал Раби , где на этой частоте действительно происходит $\delta$ — это отстройка , мера того, насколько свет находится вне резонанса относительно перехода. Например, исследуя приведенную выше анимацию при частоте смещения ±1,73, можно увидеть, что во время 1/2 цикла Раби (при резонансе), показанного во время анимации, колебание вместо этого подвергается одному полному циклу, то есть в два раза больше (нормального) Частота Раби $\Omega _{i,j}$, как и предсказывает это уравнение. Также обратите внимание, что по мере дальнейшего отклонения частоты падающего света от частоты перехода амплитуда колебаний Раби уменьшается, как показано пунктирной огибающей на графике выше.

Двухфотонная частота Раби

Когерентные осцилляции Раби также могут быть вызваны двухфотонными переходами . В этом случае мы рассматриваем систему с тремя атомными энергетическими уровнями: $|1\rangle$, $|i\rangle$, и $|2\rangle$, где $|i\rangle$ представляет собой так называемое промежуточное состояние с соответствующей частотой $\omega _{i}$, и электромагнитное поле с двумя частотными компонентами:

$${\hat {V}}(t)=e\mathbf {r} \cdot \mathbf {E} _{L1}\cos(\omega _{L1}t)+e\mathbf {r} \cdot \mathbf {E} _{L2}\cos(\omega _{L2}t)$$

Сейчас, $\omega _{i}$ может быть намного больше, чем оба $\omega _{1}$ и $\omega _{2}$, или $\omega _{2}>\omega _{i}>\omega _{1}$, как показано на рисунке справа.

Схема двухфотонного возбуждения. $\omega _{i}>>\omega _{2}>\omega _{1}$ показано слева, а $\omega _{2}>\omega _{i}>\omega _{1}$ показано справа. Вертикальная ось — это ось частоты (или энергии).

Двухфотонный переход — это не то же самое, что возбуждение из основного состояния в промежуточное, а затем из промежуточного состояния в возбужденное. Вместо этого атом поглощает два фотона одновременно и перемещается непосредственно между начальным и конечным состояниями. Есть два необходимых условия для того, чтобы этот двухфотонный процесс (также известный как рамановский процесс ) стал доминирующей моделью взаимодействия света и материи:

$${\begin{aligned}\omega _{L2}+\omega _{L1}&=\omega _{1}-\omega _{2}\\\Delta =|\omega _{L1}-\omega _{1}|&>>0\end{aligned}}$$

Другими словами, сумма частот двух фотонов должна находиться в резонансе с переходом между начальным и конечным состояниями, а отдельные частоты фотонов должны быть отстроены от промежуточного состояния к переходам в начальное и конечное состояния. Если последнее условие не выполнено и $\Delta \to 0$, доминирующим процессом будет тот, который управляется уравнениями скорости, в которых промежуточное состояние заселяется и стимулируется, а события спонтанного излучения из этого состояния предотвращают возможность возникновения когерентных колебаний между начальным и конечным состояниями.

Мы можем получить двухфотонную частоту Раби, вернувшись к уравнениям

$${\begin{aligned}i{\dot {c}}_{1}(t)&={\frac {\Omega _{1i}c_{2}}{2}}e^{i\Delta t}\\i{\dot {c}}_{i}(t)&={\frac {\Omega _{1i}^{*}c_{1}}{2}}e^{-i\Delta t}\end{aligned}}$$

которые теперь описывают возбуждение между основным и промежуточным состояниями. Мы знаем, что у нас есть решение

$$c_{i}(t)={\frac {\Omega _{1i}\sin {\bigg (}{\frac {{\tilde {\Omega }}_{1i}t}{2}}{\bigg )}}{{\tilde {\Omega }}_{1i}}}$$

где ${\tilde {\Omega }}_{1i}$ – обобщенная частота Раби перехода из начального в промежуточное состояние. Аналогично для перехода от промежуточного состояния к конечному мы имеем уравнения

$${\begin{aligned}i{\dot {c}}_{i}(t)&={\frac {\Omega _{i2}c_{2}}{2}}e^{i\Delta t}\\i{\dot {c}}_{2}(t)&={\frac {\Omega _{i2}^{*}c_{i}}{2}}e^{-i\Delta t}\end{aligned}}$$

Теперь мы подключаем $c_{i}(t)$ в приведенное выше уравнение для ${\dot {c}}_{2}(t)$

$$i{\dot {c}}_{2}(t)={\frac {\Omega _{i2}^{*}\Omega _{1i}\sin {\bigg (}{\frac {{\tilde {\Omega }}_{1i}t}{2}}{\bigg )}}{2{\tilde {\Omega }}_{1i}}}e^{-i\Delta t}$$

Так что, решив это уравнение, мы найдем коэффициент, пропорциональный:

$$c_{2}(t)\propto {\frac {\Omega _{i2}\Omega _{1i}}{2\Delta }}$$

Это эффективная или двухфотонная частота Раби. Это произведение отдельных частот Раби для $|1\rangle \to |i\rangle$ и $|i\rangle \to |2\rangle$ переходы, разделенные отстройкой от промежуточного состояния $|i\rangle$.

См. также

• Цикл Раби
• Вакуумные колебания Раби
• Метод резонанса Раби