Квантовое машинное обучение

Квантовое машинное обучение — это интеграция квантовых алгоритмов в машинного обучения . программы

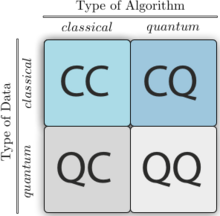
Наиболее распространенное использование этого термина относится к алгоритмам машинного обучения для анализа классических данных, выполняемых на квантовом компьютере , то есть машинному обучению с квантовым расширением. В то время как алгоритмы машинного обучения используются для вычисления огромных объемов данных, квантовое машинное обучение использует кубиты и квантовые операции или специализированные квантовые системы для повышения скорости вычислений и хранения данных, выполняемых алгоритмами в программе. Сюда входят гибридные методы, включающие как классическую, так и квантовую обработку, при которой сложные в вычислительном отношении подпрограммы передаются на аутсорсинг квантовому устройству. Эти процедуры могут быть более сложными по своей природе и выполняться быстрее на квантовом компьютере. Более того, квантовые алгоритмы можно использовать для анализа квантовых состояний вместо классических данных.

Помимо квантовых вычислений, термин «обучение квантовых машин» также связан с классическими методами машинного обучения, применяемыми к данным, полученным в результате квантовых экспериментов (т. е. машинному обучению квантовых систем ), таким как изучение фазовых переходов квантовой системы. или создание новых квантовых экспериментов.

Квантовое машинное обучение также распространяется на отрасль исследований, изучающую методологические и структурные сходства между определенными физическими системами и системами обучения, в частности нейронными сетями. Например, некоторые математические и численные методы квантовой физики применимы к классическому глубокому обучению и наоборот.

Кроме того, исследователи исследуют более абстрактные понятия теории обучения в отношении квантовой информации, иногда называемые «теорией квантового обучения».

Четыре разных подхода к объединению дисциплин квантовых вычислений и машинного обучения. Первая буква обозначает, является ли изучаемая система классической или квантовой, а вторая буква определяет, используется ли классическое или квантовое устройство обработки информации.

Машинное обучение с помощью квантовых компьютеров

Квантовое машинное обучение относится к квантовым алгоритмам , которые решают задачи машинного обучения, тем самым улучшая и часто ускоряя классические методы машинного обучения. Такие алгоритмы обычно требуют кодирования заданного классического набора данных в квантовом компьютере, чтобы сделать его доступным для обработки квантовой информации. Впоследствии применяются процедуры квантовой обработки информации, и результат квантовых вычислений считывается путем измерения квантовой системы. Например, результат измерения кубита показывает результат задачи двоичной классификации. полномасштабного универсального квантового компьютера Хотя многие предложения алгоритмов квантового машинного обучения все еще являются чисто теоретическими и требуют тестирования , другие были реализованы на небольших квантовых устройствах или квантовых устройствах специального назначения.

Квантовая ассоциативная память и

Ассоциативная память (или память с адресацией по содержимому) способна распознавать сохраненный контент на основе меры сходства, а не фиксированных адресов, как в памяти с произвольным доступом. Таким образом, они должны иметь возможность извлекать как неполные, так и поврежденные шаблоны, что является важной задачей машинного обучения по распознаванию образов.

Типичная классическая ассоциативная память хранит p-паттерны в $O(n^{2})$ взаимодействия (синапсы) реальной симметричной энергетической матрицы в сети из n искусственных нейронов. Кодирование таково, что желаемые шаблоны представляют собой локальные минимумы функционала энергии, а извлечение осуществляется путем минимизации полной энергии, начиная с начальной конфигурации.

К сожалению, классическая ассоциативная память сильно ограничена феноменом перекрестных помех . Когда сохраняется слишком много шаблонов, появляются ложные воспоминания, которые быстро размножаются, так что энергетический ландшафт становится беспорядочным и восстановление становится невозможным. Количество сохраняемых шаблонов обычно ограничено линейной функцией количества нейронов: $p\leq O(n)$.

Квантовая ассоциативная память (в их простейшей реализации) хранят шаблоны в унитарной матрице U, действующей в гильбертовом пространстве из n кубитов. Поиск реализуется путем унитарной эволюции фиксированного начального состояния к квантовой суперпозиции желаемых шаблонов с распределением вероятностей, имеющим максимум на шаблоне, наиболее похожем на входные данные. Таким образом, по своей квантовой природе процесс поиска является вероятностным. Однако, поскольку квантовая ассоциативная память свободна от перекрестных помех, ложные воспоминания никогда не генерируются. Соответственно, они имеют превосходящую емкость, чем классические. Число параметров в унитарной матрице U равно $O(pn)$. Таким образом, можно иметь эффективную квантовую ассоциативную память без ложной памяти для любого полиномиального числа паттернов.

линейной алгебры с

Ряд квантовых алгоритмов машинного обучения основан на идее амплитудного кодирования, то есть связывания амплитуд квантового состояния с входными и выходными данными вычислений. Поскольку состояние $n$ кубиты описываются $2^{n}$ комплексных амплитуд, это кодирование информации может обеспечить экспоненциально компактное представление. Интуитивно это соответствует сопоставлению дискретного распределения вероятностей двоичных случайных величин с классическим вектором. Целью алгоритмов, основанных на амплитудном кодировании, является формулирование квантовых алгоритмов, ресурсы которых растут полиномиально по числу кубитов. $n$, что соответствует логарифмической временной сложности количества амплитуд и, следовательно, размерности входных данных.

Многие алгоритмы квантового машинного обучения в этой категории основаны на вариациях квантового алгоритма для линейных систем уравнений. (в просторечии называемый HHL по имени авторов статьи), который при определенных условиях выполняет инверсию матрицы, используя количество физических ресурсов, растущих только логарифмически по размерам матрицы. Одним из этих условий является то, что гамильтониан , который по входу соответствует матрице, может быть эффективно смоделирован, что, как известно, возможно, если матрица разрежена. или низкого ранга. Для справки: любой известный классический алгоритм обращения матрицы требует ряда операций, размерность которых возрастает более чем квадратично (например, $O{\mathord {\left(n^{2.373}\right)}}$), но они не ограничиваются разреженными матрицами.

Инверсию квантовой матрицы можно применять к методам машинного обучения, в которых обучение сводится к решению линейной системы уравнений , например, в линейной регрессии наименьших квадратов, методом наименьших квадратов версия машины опорных векторов , и гауссовские процессы.

Решающим узким местом методов, моделирующих вычисления линейной алгебры с амплитудами квантовых состояний, является подготовка состояния, которая часто требует инициализации квантовой системы в состоянии, амплитуды которого отражают особенности всего набора данных. Хотя для конкретных случаев известны эффективные методы подготовки государства, этот шаг легко скрывает сложность задачи.

Вариационные квантовые алгоритмы (ВКА)

VQA являются одним из наиболее изученных квантовых алгоритмов, поскольку исследователи ожидают, что все необходимые приложения для квантового компьютера будут использовать VQA, а также VQA, похоже, оправдывают ожидания достижения квантового превосходства. VQAs — это смешанный квантово-классический подход, при котором квантовый процессор подготавливает квантовые состояния и выполняет измерения, а оптимизацию выполняет классический компьютер. VQA считаются лучшими для NISQ, поскольку VQA устойчивы к шуму по сравнению с другими алгоритмами и обеспечивают квантовое превосходство всего за несколько сотен кубитов. Исследователи изучили схемные алгоритмы для решения задач оптимизации и поиска энергии основного состояния сложных систем, которые было трудно решить или которые требовали большого времени для выполнения вычислений с использованием классического компьютера.

Вариационные квантовые схемы (ВКК)

Вариационные квантовые схемы, также известные как параметризованные квантовые схемы (PQC), основаны на вариационных квантовых алгоритмах (VQA). VQC состоят из трех частей: подготовка начальных состояний, квантовая схема и измерение. Исследователи активно изучают VQC, поскольку он использует возможности квантовых вычислений для быстрого обучения, а также использует меньше параметров, чем его классические аналоги. Теоретически и численно доказано, что мы можем аппроксимировать нелинейные функции, подобные тем, которые используются в нейронных сетях, на квантовых схемах. Из-за превосходства VQC нейронная сеть была заменена VQC в задачах обучения с подкреплением и генеративных алгоритмах. Внутренняя природа квантовых устройств, связанная с декогерентностью, случайными ошибками вентиля и ошибками измерений, привела к тому, что они имеют высокий потенциал ограничения обучения вариационных схем. Обучение VQC на классических устройствах перед их использованием на квантовых устройствах помогает преодолеть проблему шума декогеренции, возникающего из-за количества повторений обучения.

Квантовый

Реорганизация шаблонов — одна из важных задач машинного обучения, а двоичная классификация — один из инструментов или алгоритмов для поиска шаблонов. Бинарная классификация используется в обучении с учителем и в обучении без учителя . В квантовом машинном обучении классические биты преобразуются в кубиты и отображаются в гильбертово пространство; данные комплексных значений используются в квантовом двоичном классификаторе, чтобы использовать преимущества гильбертова пространства. Используя квантово-механические свойства, такие как суперпозиция, запутанность, интерференция, квантовый бинарный классификатор дает точный результат за короткий период времени.

основе поиска

Другой подход к улучшению классического машинного обучения с помощью квантовой обработки информации использует методы усиления амплитуды, основанные на алгоритме поиска Гровера , который, как было показано, решает задачи неструктурированного поиска с квадратичным ускорением по сравнению с классическими алгоритмами. Эти квантовые процедуры можно использовать для обучения алгоритмов, которые преобразуются в задачу неструктурированного поиска, как это можно сделать, например, в случае с k-медианами. и алгоритмы k-ближайших соседей . Другие приложения включают квадратичное ускорение при обучении персептрона. и расчет внимания .

Примером усиления амплитуды, используемого в алгоритме машинного обучения, является минимизация алгоритма поиска Гровера. В котором подпрограмма использует алгоритм поиска Гровера, чтобы найти элемент, меньший, чем некоторый ранее определенный элемент. Это можно сделать с помощью оракула, который определяет, меньше ли состояние с соответствующим элементом предопределенного. Алгоритм Гровера затем сможет найти элемент, удовлетворяющий нашему условию. Минимизация инициализируется некоторым случайным элементом в нашем наборе данных и итеративно выполняет эту подпрограмму, чтобы найти минимальный элемент в наборе данных. Эта минимизация особенно используется в квантовых k-медианах и имеет ускорение как минимум $O({\sqrt {n/k}})$ по сравнению с классическими версиями k-медиан, где $n$ количество точек данных и $k$ это количество кластеров.

Усиление амплитуды часто комбинируется с квантовыми блужданиями для достижения того же квадратичного ускорения. Квантовые блуждания были предложены для улучшения алгоритма PageRank Google. а также производительность агентов обучения с подкреплением в рамках проективного моделирования.

Квантовое

Обучение с подкреплением — это отрасль машинного обучения, отличная от обучения с учителем и без учителя, которая также допускает квантовые улучшения. При обучении с квантовым подкреплением квантовый агент взаимодействует с классической или квантовой средой и иногда получает вознаграждение за свои действия, что позволяет агенту адаптировать свое поведение — другими словами, узнать, что делать, чтобы получить больше вознаграждений. В некоторых ситуациях, либо из-за возможностей квантовой обработки агента, или из-за возможности исследовать окружающую среду в суперпозициях , может быть достигнуто квантовое ускорение. Реализации такого рода протоколов были предложены для систем захваченных ионов. и сверхпроводящие цепи . Квантовое ускорение внутреннего времени принятия решений агентом. было экспериментально продемонстрировано на захваченных ионах, в то время как квантовое ускорение времени обучения при полностью когерентном («квантовом») взаимодействии агента и окружающей среды было экспериментально реализовано на фотонной установке.

Квантовый отжиг

Основная статья: Квантовый отжиг

Квантовый отжиг — это метод оптимизации, используемый для определения локальных минимумов и максимумов функции по заданному набору функций-кандидатов. Это метод дискретизации функции со многими локальными минимумами или максимумами с целью определения наблюдаемых функции. Этот процесс можно отличить от имитации отжига с помощью процесса квантового туннелирования , при котором частицы туннелируют через кинетические или потенциальные барьеры из высокого состояния в низкое состояние. Квантовый отжиг начинается с суперпозиции всех возможных состояний системы, имеющих одинаковый вес. Затем зависящее от времени уравнение Шредингера направляет эволюцию системы во времени, влияя на амплитуду каждого состояния с увеличением времени. В конце концов, основное состояние может быть достигнуто, что приведет к мгновенному гамильтониану системы.

NISQ как

По мере увеличения глубины квантовой схемы на устройствах NISQ уровень шума растет, что создает серьезную проблему для точного расчета затрат и градиентов в обучающих моделях. Устойчивость к шуму будет повышена за счет использования квантового персептрона и квантового алгоритма на доступном в настоящее время квантовом оборудовании.

Регулярное соединение подобных компонентов, известных как нейроны, составляет основу даже самых сложных сетей мозга. Обычно нейрон выполняет две операции: внутренний продукт и функцию активации . В отличие от функции активации, которая обычно является нелинейной , внутренний продукт представляет собой линейный процесс. С помощью квантовых вычислений можно легко дополнительно реализовать линейные процессы, поскольку из-за простоты реализации большинство квантовых нейронов предпочитают пороговую функцию для функций активации.

выборки

Выборка из многомерных распределений вероятностей лежит в основе широкого спектра вычислительных методов, имеющих важные приложения в науке, технике и обществе. Примеры включают глубокое обучение , вероятностное программирование и другие приложения машинного обучения и искусственного интеллекта.

Вычислительно сложной проблемой, которая является ключевой для некоторых соответствующих задач машинного обучения, является оценка средних значений по вероятностным моделям, определенным в терминах распределения Больцмана . Выборка из общих вероятностных моделей сложна: ожидается, что алгоритмы, в значительной степени полагающиеся на выборку, останутся трудноразрешимыми, независимо от того, насколько большими и мощными станут классические вычислительные ресурсы. Несмотря на то, что квантовые отжиги, подобные тем, что производятся D-Wave Systems, были разработаны для решения сложных задач комбинаторной оптимизации, недавно они были признаны потенциальным кандидатом для ускорения вычислений, основанных на выборке, за счет использования квантовых эффектов.

Некоторые исследовательские группы недавно изучили возможность использования оборудования квантового отжига для обучения машин Больцмана и глубоких нейронных сетей . Стандартный подход к обучению машин Больцмана основан на вычислении определенных средних значений, которые можно оценить с помощью стандартных методов выборки , таких как Монте-Карло с использованием цепей Маркова алгоритмы . Другая возможность — полагаться на физический процесс, такой как квантовый отжиг, который естественным образом генерирует образцы из распределения Больцмана. Цель состоит в том, чтобы найти оптимальные параметры управления, которые лучше всего отражают эмпирическое распределение данного набора данных.

Система D-Wave 2X, размещенная в Исследовательском центре Эймса НАСА, недавно использовалась для обучения специального класса ограниченных машин Больцмана, которые могут служить строительным блоком для архитектур глубокого обучения. Дополнительные работы, появившиеся примерно одновременно, показали, что квантовый отжиг можно использовать для контролируемого обучения в задачах классификации. Позже это же устройство было использовано для обучения полностью подключенной машины Больцмана генерированию, реконструкции и классификации уменьшенных рукописных цифр с низким разрешением среди других синтетических наборов данных. В обоих случаях модели, обученные с помощью квантового отжига, имели аналогичные или лучшие характеристики с точки зрения качества. Главный вопрос, который движет этими усилиями, заключается в том, существует ли квантовое ускорение в приложениях выборки. Опыт использования квантовых отжигов для комбинаторной оптимизации показывает, что ответ не однозначен. Обратный отжиг также использовался для решения полностью связной квантово-ограниченной машины Больцмана.

Вдохновленный успехом машин Больцмана, основанных на классическом распределении Больцмана, недавно был предложен новый подход к машинному обучению, основанный на квантовом распределении Больцмана гамильтониана Изинга поперечного поля. Из-за некоммутативной природы квантовой механики процесс обучения квантовой машины Больцмана может стать нетривиальным. Эту проблему в некоторой степени удалось обойти, введя ограничения на квантовые вероятности, что позволило авторам эффективно обучать модель путем выборки. Вполне возможно, что определенный тип квантовой машины Больцмана был обучен в D-Wave 2X с использованием правила обучения, аналогичного правилу обучения классических машин Больцмана.

Квантовый отжиг — не единственная технология отбора проб. В сценарии «подготовь и измерь» универсальный квантовый компьютер подготавливает тепловое состояние, которое затем измеряется с помощью измерений. Это может сократить время, необходимое для обучения машины Больцмана с глубокими ограничениями, и обеспечить более богатую и всеобъемлющую основу для глубокого обучения, чем классические вычисления. Те же квантовые методы также позволяют эффективно обучать полные машины Больцмана и многослойные полностью связные модели и не имеют хорошо известных классических аналогов. Опираясь на эффективный протокол подготовки теплового состояния, начиная с произвольного состояния, марковские логические сети с квантовым расширением используют симметрию и структуру локальности вероятностной графической модели, сгенерированной логическим шаблоном первого порядка . Это обеспечивает экспоненциальное снижение вычислительной сложности при вероятностном выводе, и, хотя протокол основан на универсальном квантовом компьютере, при мягких предположениях его можно внедрить в современное оборудование для квантового отжига.

Квантовые нейронные сети

Основная статья: Квантовая нейронная сеть

Квантовые аналоги или обобщения классических нейронных сетей часто называют квантовыми нейронными сетями . Этот термин востребован широким спектром подходов, включая реализацию и расширение нейронных сетей с использованием фотонов, слоистых вариационных схем или квантовых моделей типа Изинга. Квантовые нейронные сети часто определяют как расширение модели квантовой вычислительной сети Дойча. В рамках этой модели для спекуляции данного набора данных используются нелинейные и необратимые элементы, отличные от оператора Гамильтона. Такие ворота делают невозможным наблюдение определенных фаз и генерируют определенные колебания. Квантовые нейронные сети применяют принципы квантовой информации и квантовых вычислений к классическим нейрокомпьютерам. Текущие исследования показывают, что QNN может экспоненциально увеличивать вычислительную мощность и степени свободы компьютера, которые для классического компьютера ограничены его размером. Квантовая нейронная сеть обладает вычислительными возможностями, позволяющими уменьшить количество шагов, используемых кубитов и время вычислений. Волновая функция в квантовой механике — это нейрон для нейронных сетей. Для тестирования квантовых приложений в нейронной сети молекулы квантовых точек наносятся на подложку из GaAs или аналогичного материала, чтобы записать, как они взаимодействуют друг с другом. Каждую квантовую точку можно назвать островком электрической активности, и когда такие точки расположены достаточно близко (приблизительно 10–20 нм) электроны могут туннелировать под островами. Равномерное распределение по подложке в наборах по два создает диполи и, в конечном итоге, два состояния спина: вверх или вниз. Эти состояния обычно известны как кубиты с соответствующими состояниями $|0\rangle$ и $|1\rangle$ в обозначениях Дирака.

свертки

Новый дизайн многомерных векторов, в котором схемы используются в качестве фильтров свертки. это QCNN. Он был вдохновлен преимуществами CNN. и мощь QML. Это сделано с использованием комбинации вариационной квантовой схемы (VQC). и глубокая нейронная сеть (DNN), полностью используя возможности чрезвычайно параллельной обработки суперпозиции квантового состояния с конечным числом кубитов. Основная стратегия заключается в проведении итеративного процесса оптимизации в NISQ. устройств без негативного влияния шума, который, возможно, заложен в параметре схемы, и без необходимости квантовой коррекции ошибок.

Квантовая схема должна эффективно обрабатывать пространственную информацию, чтобы QCNN функционировала как CNN. Сверточный фильтр — это самый простой метод использования пространственной информации. Один или несколько квантовых сверточных фильтров составляют квантовую сверточную нейронную сеть (QCNN), и каждый из этих фильтров преобразует входные данные с помощью квантовой схемы, которая может быть создана организованным или рандомизированным способом. Квантовый сверточный фильтр состоит из трех частей: кодировщик, параметризованная квантовая схема (PQC), и измерение. Квантовый сверточный фильтр можно рассматривать как расширение фильтра традиционной CNN, поскольку он был разработан с обучаемыми параметрами.

Квантовые нейронные сети используют преимущества иерархических структур, и для каждого последующего слоя количество кубитов предыдущего слоя уменьшается в два раза. Для n входных кубитов эта структура имеет слои O(log(n)) что обеспечивает небольшую глубину схемы. Кроме того, они могут избежать «бесплодного плато», одной из наиболее серьезных проблем алгоритмов на основе PQC, обеспечивая обучаемость. Несмотря на то, что модель QCNN не включает соответствующую квантовую операцию, для обеспечения достоверности также предлагается фундаментальная идея уровня пула. В архитектуре QCNN уровень объединения обычно размещается между последующими сверточными уровнями. Его функция состоит в том, чтобы уменьшить пространственный размер представления при сохранении важнейших функций, что позволяет уменьшить количество параметров, оптимизировать сетевые вычисления и управлять переобучением. Такой процесс можно осуществить, применив полную томографию состояния, чтобы полностью уменьшить его до одного кубита, а затем обработать его в метро. Наиболее часто используемый тип единиц на уровне пула — это максимальный пул, хотя существуют и другие типы. Подобно обычным нейронным сетям с прямой связью , последний модуль представляет собой полностью связанный уровень с полными связями со всеми активациями на предыдущем уровне. Трансляционная инвариантность, которая требует идентичных блоков параметризованных квантовых вентилей внутри слоя, является отличительной чертой архитектуры QCNN.

сеть

Диссипативные QNN (DQNN) состоят из слоев кубитов, связанных перцептроном, называемых строительными блоками, которые имеют произвольную унитарную конструкцию. Каждому узлу сетевого уровня DQNN дан отдельный набор кубитов, и каждому кубиту также дается уникальный унитарный квантовый перцептрон, который характеризует его. Информация о входных состояниях передается по сети в режиме прямой связи, отображение переходов между слоями на кубитах двух соседних слоев, как следует из названия. Термин «диссипативность» также относится к тому факту, что выходной слой формируется вспомогательными кубитами, в то время как входные слои отбрасываются при трассировке последнего слоя. При выполнении широкой задачи обучения с учителем DQNN используются для изучения унитарной матрицы, соединяющей входные и выходные квантовые состояния. Обучающие данные для этой задачи состоят из квантового состояния и соответствующих классических меток.

Вдохновленный чрезвычайно успешной классической генеративно-состязательной сетью (GAN) , диссипативная квантовая генеративно-состязательная сеть (DQGAN) представлена ​​для неконтролируемого обучения немаркированных обучающих данных. Генератор и дискриминатор — это две DQNN, составляющие одну DQGAN. Цель генератора — создать ложные состояния обучения, которые дискриминатор не сможет отличить от подлинных, а цель дискриминатора — отделить настоящие состояния обучения от ложных состояний, созданных генератором. Соответствующие функции обучающего набора изучаются генератором путем альтернативного и состязательного обучения сетей, которые помогают создавать наборы, расширяющие обучающий набор. DQGAN имеет полностью квантовую архитектуру и обучен на квантовых данных.

марковские

Скрытые квантовые модели Маркова (HQMM) — это квантово-расширенная версия классических скрытых марковских моделей (HMM), которые обычно используются для моделирования последовательных данных в различных областях, таких как робототехника и обработка естественного языка . В отличие от подхода, используемого другими алгоритмами квантового машинного обучения, HQMM можно рассматривать как модели, основанные на квантовой механике, которые также можно запускать на классических компьютерах. В то время как классические HMM используют векторы вероятности для представления скрытых состояний «убеждения», HQMM используют квантовый аналог: матрицы плотности . Недавняя работа показала, что эти модели можно успешно изучить за счет максимизации логарифмического правдоподобия заданных данных посредством классической оптимизации, и есть некоторые эмпирические доказательства того, что на практике эти модели могут лучше моделировать последовательные данные по сравнению с классическими HMM, хотя дальнейшая работа еще не завершена. необходимо точно определить, когда и как будут получены эти выгоды. Кроме того, поскольку классические HMM представляют собой особый вид сети Байеса , захватывающим аспектом HQMM является то, что используемые методы показывают, как мы можем выполнить квантово-аналоговый байесовский вывод , который должен позволить общее построение квантовых версий вероятностных графических моделей .

машинное

В самом общем случае квантового машинного обучения и обучающее устройство, и изучаемая система, а также их взаимодействие являются полностью квантовыми. В этом разделе приведены несколько примеров результатов по этой теме.

Одним из классов проблем, для которых может быть полезен полностью квантовый подход, является «обучение» неизвестных квантовых состояний, процессов или измерений в том смысле, что их можно впоследствии воспроизвести в другой квантовой системе. Например, кто-то может захотеть изучить измерение, которое различает два когерентных состояния, имея не классическое описание различаемых состояний, а вместо этого набор примеров квантовых систем, подготовленных в этих состояниях. Наивный подход заключался бы в том, чтобы сначала извлечь классическое описание состояний, а затем реализовать идеальное избирательное измерение на основе этой информации. Для этого потребуется только классическое обучение. Однако можно показать, что полностью квантовый подход в этом случае имеет явное преимущество. (Это также относится к работе по сопоставлению квантовых образов. ) Аналогично можно подойти к задаче изучения унитарных преобразований.

Выходя за рамки конкретной проблемы изучения состояний и преобразований, задача кластеризации также допускает полностью квантовую версию, в которой как оракул, возвращающий расстояние между точками данных, так и устройство обработки информации, запускающее алгоритм, являются квантовыми. Наконец, в полностью квантовой среде была представлена ​​общая структура, охватывающая контролируемое, неконтролируемое обучение и обучение с подкреплением. где также было показано, что возможность исследования окружающей среды в суперпозициях позволяет квантово ускорить обучение с подкреплением. Такое ускорение в парадигме обучения с подкреплением было экспериментально продемонстрировано на фотонной установке.

машинное

Потребность в моделях, понятных людям, возникает в квантовом машинном обучении по аналогии с классическим машинным обучением и стимулирует исследовательскую область объяснимого квантового машинного обучения (или XQML). по аналогии с XAI/XML ). Эти усилия часто также называют интерпретируемым машинным обучением (IML и, как следствие, IQML). XQML/IQML можно рассматривать как альтернативное направление исследований вместо поиска квантового преимущества. Например, XQML использовался в контексте обнаружения и классификации мобильных вредоносных программ. Квантовые значения Шепли также были предложены для интерпретации вентилей внутри схемы на основе теоретико-игрового подхода. Для этой цели ворота вместо функций выступают в роли игроков в коалиционной игре с функцией ценности, которая зависит от измерений интересующей квантовой схемы. Кроме того, квантовая версия классической техники, известная как LIME (линейные интерпретируемые модельно-агностические объяснения). также был предложен продукт, известный как Q-LIME.

Классическое обучение применительно

Дополнительная информация: Машинное обучение в физике.

Термин «квантовое машинное обучение» иногда относится к классическому машинному обучению, выполняемому на данных из квантовых систем. Базовым примером этого является томография квантовых состояний , где квантовое состояние изучается в результате измерений. Другие приложения включают изучение гамильтонианов. и автоматически проводить квантовые эксперименты.

обучения

Теория квантового обучения преследует математический анализ квантовых обобщений классических моделей обучения и возможных ускорений или других улучшений, которые они могут обеспечить. Структура очень похожа на классическую теорию вычислительного обучения , но обучаемый в данном случае представляет собой квантовое устройство обработки информации, а данные могут быть как классическими, так и квантовыми. Теорию квантового обучения следует противопоставлять квантово-расширенному машинному обучению, обсуждавшемуся выше, целью которого было рассмотрение конкретных проблем и использование квантовых протоколов для улучшения временной сложности классических алгоритмов для решения этих задач. Хотя теория квантового обучения все еще находится в стадии разработки, частичные результаты в этом направлении уже получены.

Отправной точкой в ​​теории обучения обычно является класс концепций, набор возможных концепций. Обычно понятие — это функция в какой-то области, например $\{0,1\}^{n}$. Например, концептуальный класс может представлять собой набор формул дизъюнктивной нормальной формы (ДНФ) на n битах или набор логических схем некоторой постоянной глубины. Цель учащегося — изучить (точно или приблизительно) неизвестную целевую концепцию из этого класса концепций. Учащийся может активно взаимодействовать с целевой концепцией или пассивно получать из нее образцы.

При активном обучении учащийся может делать запросы на принадлежность к целевому понятию c, запрашивая его значение c(x) на входных данных x, выбранных учащимся. Затем учащийся должен с высокой вероятностью восстановить точную целевую концепцию. В модели квантового точного обучения учащийся может делать запросы на членство в квантовой суперпозиции. Если сложность учащегося измеряется количеством выполняемых им запросов на членство, то квантово-точные учащиеся могут быть полиномиально более эффективными, чем классические учащиеся, для некоторых концептуальных классов, но не более того. Если сложность измеряется количеством времени, которое учащийся использует, то существуют концептуальные классы, которые могут эффективно изучать квантовые учащиеся, но не классические учащиеся (при правдоподобных предположениях теории сложности).

Естественная модель пассивного обучения — это вероятно приблизительно правильное (PAC) обучение Valiant . Здесь учащийся получает случайные примеры (x,c(x)), где x распределяется в соответствии с некоторым неизвестным распределением D. Цель учащегося — вывести функцию гипотезы h такую, что h(x)=c(x) с высокой вероятностью. когда x нарисован в соответствии с D. Обучающийся должен быть в состоянии создать такой «приблизительно правильный» h для каждого D и каждого целевого понятия c в своем классе понятий. Мы можем рассмотреть возможность замены случайных примеров потенциально более мощными квантовыми примерами. $\sum _{x}{\sqrt {D(x)}}|x,c(x)\rangle$. В модели PAC (и связанной с ней агностической модели) это существенно не уменьшает количество необходимых примеров: для каждого класса концепций сложность классической и квантовой выборки одинакова с точностью до постоянных коэффициентов. Однако для обучения при некотором фиксированном распределении D квантовые примеры могут быть очень полезны, например, для изучения ДНФ при равномерном распределении. При рассмотрении временной сложности существуют концептуальные классы, которые квантовые обучающиеся могут эффективно изучить с помощью PAC, даже на классических примерах, но не классические обучающиеся (опять же, при правдоподобных предположениях теории сложности).

Этот тип пассивного обучения также является наиболее распространенной схемой обучения с учителем: алгоритм обучения обычно использует фиксированные обучающие примеры без возможности запрашивать метки немаркированных примеров. Вывод гипотезы h является шагом индукции. Классически индуктивная модель разделяется на этап обучения и этап применения: параметры модели оцениваются на этапе обучения, а изученная модель применяется произвольное количество раз на этапе применения. В асимптотическом пределе числа приложений такое расщепление фаз присутствует и с квантовыми ресурсами.

Реализации и эксперименты

Самые ранние эксперименты были проведены с использованием адиабатического квантового компьютера D-Wave , например, для обнаружения автомобилей на цифровых изображениях с использованием регуляризованного повышения с невыпуклой целевой функцией во время демонстрации в 2009 году. На одной и той же архитектуре последовало множество экспериментов, и ведущие технологические компании проявили интерес к потенциалу квантового машинного обучения для будущих технологических реализаций. В 2013 году исследовательский центр Google, НАСА и Ассоциация университетских космических исследований запустили Лабораторию квантового искусственного интеллекта , которая исследует использование адиабатического квантового компьютера D-Wave. Более свежий пример обучил вероятностные генеративные модели с произвольной парной связностью, показав, что их модель способна генерировать рукописные цифры, а также реконструировать зашумленные изображения полос, полос и рукописных цифр.

В 2009 году с использованием другой технологии отжига, основанной на ядерном магнитном резонансе (ЯМР), была реализована квантовая сеть Хопфилда , которая сопоставила входные данные и запомнила данные с гамильтонианами, что позволило использовать адиабатические квантовые вычисления. Технология ЯМР также обеспечивает универсальные квантовые вычисления, и он использовался для первой экспериментальной реализации квантовой машины опорных векторов для распознавания рукописных цифр «6» и «9» на жидкостном квантовом компьютере в 2015 году. Данные обучения включали предварительную обработку изображения, которая сопоставляла их с нормализованными двумерными векторами, чтобы представить изображения как состояния кубита. Две записи вектора представляют собой соотношение интенсивности пикселей изображения по вертикали и горизонтали. После того как векторы определены в пространстве признаков , была реализована машина квантовых опорных векторов для классификации неизвестного входного вектора. Считывание позволяет избежать дорогостоящей квантовой томографии за счет считывания конечного состояния с точки зрения направления (вверх/вниз) сигнала ЯМР.

Фотонные реализации привлекают все больше внимания. не в последнюю очередь потому, что они не требуют значительного охлаждения. В 2013 году одновременное распознавание произнесенных цифр и говорящего, а также хаотическое прогнозирование временных рядов было продемонстрировано при скорости передачи данных более 1 гигабайта в секунду. Используя нелинейную фотонику для реализации полностью оптического линейного классификатора, модель перцептрона была способна итеративно изучать границу классификации на основе обучающих данных с помощью правила обратной связи. Основным строительным блоком многих алгоритмов обучения является вычисление расстояния между двумя векторами: впервые это было экспериментально продемонстрировано для восьми измерений с использованием запутанных кубитов в фотонном квантовом компьютере в 2015 году.

Недавно, на основе нейромиметического подхода, в область квантового машинного обучения был добавлен новый ингредиент в виде так называемого квантового мемристора, квантовой модели стандартного классического мемристора . Это устройство можно сконструировать с помощью перестраиваемого резистора, слабых измерений в системе и классического механизма прямой связи. Была предложена реализация квантового мемристора в сверхпроводниковых схемах. и проведен эксперимент с квантовыми точками. Квантовый мемристор будет реализовывать нелинейные взаимодействия в квантовой динамике, что поможет в поиске полнофункциональной квантовой нейронной сети.

С 2016 года IBM запустила облачную онлайн-платформу для разработчиков квантового программного обеспечения под названием IBM Q Experience . Эта платформа состоит из нескольких полностью работоспособных квантовых процессоров, доступных через веб-API IBM. При этом компания поощряет разработчиков программного обеспечения разрабатывать новые алгоритмы в среде разработки с квантовыми возможностями. На экспериментальной основе исследуются новые архитектуры, вплоть до 32 кубитов, с использованием методов квантовых вычислений как с захваченными ионами, так и со сверхпроводниками.

В октябре 2019 года было отмечено, что внедрение квантовых генераторов случайных чисел (QRNG) в модели машинного обучения, включая нейронные сети и сверточные нейронные сети для случайного начального распределения веса и случайные леса для процессов разделения, оказало глубокое влияние на их возможности по сравнению с классический метод генераторов псевдослучайных чисел (ГПСЧ). Однако в более поздней публикации 2021 года эти утверждения не удалось воспроизвести для инициализации веса нейронной сети, и не было обнаружено никаких существенных преимуществ использования QRNG перед PRNG. Работа также продемонстрировала, что генерация справедливых случайных чисел с помощью вентильного квантового компьютера является нетривиальной задачей для устройств NISQ, и поэтому QRNG обычно гораздо сложнее использовать на практике, чем PRNG.

В статье, опубликованной в декабре 2018 года, сообщается об эксперименте с использованием системы захваченных ионов, демонстрирующем квантовое ускорение времени обсуждения агентов обучения с подкреплением, использующих внутреннее квантовое оборудование.

В марте 2021 года группа исследователей из Австрии, Нидерландов, США и Германии сообщила об экспериментальной демонстрации квантового ускорения времени обучения агентов обучения с подкреплением, полностью квантово взаимодействующих с окружающей средой. Соответствующие степени свободы как агента, так и окружающей среды были реализованы на компактном и полностью настраиваемом интегрированном нанофотонном процессоре.

Скептицизм

Хотя машинное обучение само по себе сейчас является не только областью исследований, но и экономически значимой и быстрорастущей отраслью, а квантовые вычисления — хорошо зарекомендовавшей себя областью как теоретических, так и экспериментальных исследований, квантовое машинное обучение остается чисто теоретической областью исследований. Попытки экспериментально продемонстрировать концепции квантового машинного обучения остаются недостаточными.

Многие ведущие ученые, активно публикующие публикации в области квантового машинного обучения, предупреждают о масштабном ажиотаже вокруг этой темы и очень сдержанно отвечают на вопрос о ее практическом использовании в обозримом будущем. София Чен собрал некоторые высказывания известных ученых в этой области:

• «Я думаю, что мы еще не сделали домашнее задание. Это чрезвычайно новая научная область», — физик Мария Шульд из канадского стартапа по квантовым вычислениям Xanadu.
• «Смешивая машинное обучение с «квантовым», вы катализируете хайп-конденсат». - Джейкоб Биамонте внес вклад в теорию квантовых вычислений.
• «Предстоит проделать гораздо больше работы, прежде чем утверждать, что квантовое машинное обучение действительно будет работать», — учёный-компьютерщик Иорданис Керенидис, руководитель отдела квантовых алгоритмов стартапа квантовых вычислений в Кремниевой долине QC Ware.
• «Я не видел ни одного доказательства того, что существует значимая задача [машинного обучения], для решения которой имело бы смысл использовать квантовый компьютер, а не классический компьютер», — физик Райан Свеке из Свободного университета Берлина в Германии. .
• «Не поддавайтесь рекламе!» - Фрэнк Зикерт, автор, пожалуй, самой практичной книги по этой теме, помните, что «квантовые компьютеры далеки от развития машинного обучения в плане их способности представления» и даже говорят об оценке и оптимизации для любого рода полезных квантовых задач. превосходство еще не достигнуто. Более того, никто из активных исследователей в этой области не делает никаких прогнозов о том, когда это может стать практическим.

См. также

• Дифференцируемое программирование
• Квантовые вычисления
• Квантовый алгоритм для линейных систем уравнений
• Квантовый отжиг
• Квантовая нейронная сеть
• Квантовое изображение