Сеть Хопфилда
Сеть Хопфилда ( модель Изинга нейронной сети или модель Изинга-Ленца-Литтла или сеть Амари-Литтла-Хопфилда ) — это система спинового стекла , используемая для моделирования нейронных сетей , основанная на Эрнста Изинга работе с Вильгельмом Ленцем над моделью Изинга. из магнитных материалов. [1] Сети Хопфилда были впервые описаны в отношении рекуррентных нейронных сетей Шуничи Амари в 1972 году. [2] [3] а что касается биологических нейронных сетей Уильяма Литтла в 1974 году, [4] и были популяризированы Джоном Хопфилдом в 1982 году. [5] Сети Хопфилда служат содержательно-адресуемыми («ассоциативными») системами памяти с двоичными пороговыми узлами или с непрерывными переменными. [6] Сети Хопфилда также предоставляют модель для понимания человеческой памяти. [7] [8]
История [ править ]
Сама модель Изинга была опубликована в 1920-х годах как модель магнетизма, однако она изучалась при тепловом равновесии, которое не меняется со временем. Глаубер в 1963 году изучил модель Изинга, развивающуюся во времени, как процесс достижения теплового равновесия ( динамика Глаубера ). [9]
Модель модели Изинга обучения была впервые предложена Шуничи Амари в 1972 году. [2] а затем Уильямом А. Литтлом в 1974 году: [4] который был признан Хопфилдом в его статье 1982 года. Модель спинового стекла Шеррингтона -Киркпатрика , опубликованная в 1975 году, представляет собой сеть Хопфилда со случайной инициализацией. Шеррингтон и Киркпатрик обнаружили, что энергетическая функция модели SK с высокой вероятностью будет иметь множество локальных минимумов. [5]
Сети с непрерывной динамикой были разработаны Хопфилдом в его статье 1984 года. [6] Крупный прогресс в области емкости памяти был разработан Кротовым и Хопфилдом в 2016 году. [10] через изменение сетевой динамики и энергетической функции. Эта идея была развита Демирджигилом и его коллегами в 2017 году. [11] Модели непрерывной динамики памяти большой емкости были разработаны в серии статей в период с 2016 по 2020 год. [10] [12] [13] Сети Хопфилда с большой емкостью памяти теперь называются плотными ассоциативными запоминающими устройствами или современными сетями Хопфилда .
Структура [ править ]
Единицы в сетях Хопфилда являются двоичными пороговыми единицами, т. е. единицы принимают только два разных значения для своих состояний, а значение определяется тем, превышает ли входной сигнал единицы ее пороговое значение. . Дискретные сети Хопфилда описывают отношения между бинарными (активирующими или неактивными) нейронами. . [5] В определенный момент состояние нейронной сети описывается вектором , который записывает, какие нейроны срабатывают, в двоичном слове биты.
Взаимодействия Между нейронами есть единицы, которые обычно принимают значения 1 или -1, и это соглашение будет использоваться на протяжении всей статьи. Однако в другой литературе могут использоваться единицы, принимающие значения 0 и 1. Эти взаимодействия «обучаются» с помощью закона ассоциации Хебба , так что для определенного состояния и отдельные узлы
но .
(Обратите внимание, что правило обучения Хебба принимает форму когда единицы принимают значения в .)
Как только сеть будет обучена, больше не развивается. Если новое состояние нейронов вводится в нейронную сеть, сеть действует на нейроны так, что
- если
- если
где — пороговое значение i-го нейрона (часто принимается равным 0). [14] Таким образом, сети Хопфилда имеют возможность «запоминать» состояния, хранящиеся в матрице взаимодействия, поскольку если новое состояние подвергается воздействию матрицы взаимодействия, каждый нейрон будет меняться до тех пор, пока не достигнет исходного состояния (см. раздел «Обновления» ниже).
Соединения в сети Хопфилда обычно имеют следующие ограничения:
- (ни одна единица не имеет связи сама с собой)
- (соединения симметричны)
Ограничение симметрии весов гарантирует, что энергетическая функция монотонно убывает при соблюдении правил активации. [15] Сеть с асимметричными весами может демонстрировать периодическое или хаотическое поведение; однако Хопфилд обнаружил, что такое поведение ограничено относительно небольшими частями фазового пространства и не ухудшает способность сети действовать как система ассоциативной памяти с адресацией по контенту.
Хопфилд также моделировал нейронные сети для непрерывных значений, в которых электрический выход каждого нейрона является не двоичным, а некоторым значением от 0 до 1. [6] Он обнаружил, что этот тип сети также способен хранить и воспроизводить запомненные состояния.
Обратите внимание, что каждая пара модулей i и j в сети Хопфилда имеет соединение, которое описывается весом связности. . В этом смысле сеть Хопфилда формально можно описать как полный неориентированный граф. , где представляет собой набор нейронов Мак-Каллоха-Питтса и — это функция, которая связывает пары единиц с реальным значением — весом связности.
Обновление [ править ]
Обновление одной единицы (узла в графе, моделирующем искусственный нейрон) в сети Хопфилда производится по следующему правилу:
где:
- — прочность соединения веса от узла j до узла i (вес соединения).
- состояние единицы i.
- порог единицы i.
Обновления в сети Хопфилда могут выполняться двумя разными способами:
- Асинхронный : одновременно обновляется только один блок. Этот отряд можно выбрать случайным образом или с самого начала можно установить заранее определенный порядок.
- Синхронно : все устройства обновляются одновременно. Для поддержания синхронизации в системе требуются центральные часы. Некоторые считают этот метод менее реалистичным, поскольку он основан на отсутствии наблюдаемых глобальных часов, влияющих на аналогичные представляющие интерес биологические или физические системы.
притягивают или отталкивают друг друга» в состояний Нейроны « пространстве
Вес между двумя единицами оказывает сильное влияние на значения нейронов. Учитывайте вес соединения между двумя нейронами i и j. Если правило обновления подразумевает, что:
- когда , вклад j во взвешенную сумму положителен. Таким образом, притягивается j к своему значению
- когда , вклад j во взвешенную сумму отрицательный. Опять же, подталкивается j к своему значению
Таким образом, значения нейронов i и j сойдутся, если вес между ними положителен. Аналогично они будут расходиться, если вес отрицательный.
Принципы работы дискретных и непрерывных сетей Хопфилда
Брук пролил свет на поведение нейрона в дискретной сети Хопфилда, доказав ее сходимость в своей статье 1990 года. [16] Последующий документ [17] дополнительно исследовал поведение любого нейрона в сетях Хопфилда как с дискретным, так и с непрерывным временем, когда соответствующая энергетическая функция минимизируется в процессе оптимизации. Брук показывает [16] этот нейрон j меняет свое состояние тогда и только тогда, когда он дополнительно уменьшает следующий смещенный псевдоразрез. Дискретная сеть Хопфилда минимизирует следующий смещенный псевдоразрез [17] для матрицы синаптических весов сети Хопфилда.
где и представляет собой набор нейронов, которые равны -1 и +1 соответственно в момент времени . Более подробную информацию можно найти в недавней статье. [17]
Сеть Хопфилда с дискретным временем всегда минимизирует именно следующий псевдоразрез: [16] [17]
Сеть Хопфилда с непрерывным временем всегда минимизирует верхнюю границу следующего взвешенного разреза [17]
где является сигмоидальной функцией с центром в нуле.
С другой стороны, сложная сеть Хопфилда обычно имеет тенденцию минимизировать так называемое теневое сокращение матрицы комплексных весов сети. [18]
Энергия [ править ]

Сети Хопфилда имеют скалярное значение, связанное с каждым состоянием сети, называемое «энергией» E сети, где:
Это количество называется «энергией», поскольку оно либо уменьшается, либо остается неизменным при обновлении сетевых блоков. Более того, при многократном обновлении сеть в конечном итоге сходится к состоянию, которое является локальным минимумом функции энергии (которая считается функцией Ляпунова ). [5] Таким образом, если состояние является локальным минимумом энергетической функции, оно является стабильным состоянием сети. Обратите внимание, что эта энергетическая функция принадлежит к общему классу моделей в физике под названием модели Изинга ; они, в свою очередь, являются частным случаем марковских сетей , поскольку связанная с ними вероятностная мера , мера Гиббса , обладает марковским свойством .
Сеть оптимизации в Хопфилда
Хопфилд и Танк представили применение сети Хопфилда для решения классической задачи коммивояжера в 1985 году. [19] С тех пор сеть Хопфилда широко используется для оптимизации. Идея использования сети Хопфилда в задачах оптимизации проста: если ограниченную/неограниченную функцию стоимости можно записать в виде энергетической функции Хопфилда E, то существует сеть Хопфилда, точки равновесия которой представляют собой решения ограниченной/неограниченной оптимизации. проблема. Минимизация энергетической функции Хопфилда одновременно минимизирует целевую функцию и удовлетворяет ограничениям, поскольку ограничения «встроены» в синаптические веса сети. Хотя включение оптимизационных ограничений в синаптические веса наилучшим образом является сложной задачей, многие сложные задачи оптимизации с ограничениями в различных дисциплинах были преобразованы в энергетическую функцию Хопфилда: системы ассоциативной памяти, аналого-цифровое преобразование, работа задача планирования магазина, квадратичное назначение и другие связанные с ней NP-полные задачи, проблема распределения каналов в беспроводных сетях, проблема маршрутизации мобильных одноранговых сетей, восстановление изображений, идентификация системы, комбинаторная оптимизация и т. д., и это лишь некоторые из них. Более подробную информацию можно найти, например, в статье. [17]
Инициализация и запуск [ править ]
Инициализация сетей Хопфилда выполняется путем установки значений единиц в соответствии с желаемым шаблоном запуска. Затем выполняются повторные обновления до тех пор, пока сеть не сойдется к шаблону аттрактора. Сходимость в целом обеспечивается, поскольку Хопфилд доказал, что аттракторы этой нелинейной динамической системы стабильны, а не периодически или хаотичны, как в некоторых других системах. [ нужна ссылка ] . Следовательно, в контексте сетей Хопфилда шаблон аттрактора — это окончательное стабильное состояние, шаблон, который не может изменить какое-либо значение внутри себя при обновлении. [ нужна ссылка ] .
Обучение [ править ]
Обучение сети Хопфилда предполагает снижение энергии состояний, которые сеть должна «запоминать». Это позволяет сети служить системой памяти, адресуемой по контенту, то есть сеть будет переходить в «запомненное» состояние, если ей будет предоставлена только часть состояния. Сеть может использоваться для восстановления после искаженных входных данных до обученного состояния, которое наиболее похоже на эти входные данные. Это называется ассоциативной памятью, поскольку она восстанавливает воспоминания на основе сходства. Например, если мы обучим сеть Хопфилда с пятью элементами так, чтобы состояние (1, −1, 1, −1, 1) было минимумом энергии, и мы зададим сети состояние (1, −1, −1, −1, 1) оно будет сходиться к (1, −1, 1, −1, 1). Таким образом, сеть правильно обучается, когда энергия состояний, которые сеть должна запомнить, является локальным минимумом. Обратите внимание, что, в отличие от обучения персептроном , пороги нейронов никогда не обновляются.
Правила обучения [ править ]
Существуют различные правила обучения , которые можно использовать для хранения информации в памяти сети Хопфилда. Желательно, чтобы правило обучения имело оба следующих двух свойства:
- Локальное : правило обучения является локальным , если каждый вес обновляется с использованием информации, доступной нейронам по обе стороны соединения, связанного с этим конкретным весом.
- Поэтапно : новые шаблоны можно изучать без использования информации из старых шаблонов, которые также использовались для обучения. То есть, когда для обучения используется новый шаблон, новые значения весов зависят только от старых значений и нового шаблона. [20]
Эти свойства желательны, поскольку удовлетворяющее им правило обучения более биологически правдоподобно. Например, поскольку человеческий мозг постоянно изучает новые концепции, можно предположить, что человеческое обучение происходит постепенно. Система обучения, которая не была инкрементной, обычно обучалась только один раз с использованием огромного количества обучающих данных.
обучения Хебба для сетей Хопфилда Правило
Теория Хебба была предложена Дональдом Хеббом в 1949 году для объяснения «ассоциативного обучения», при котором одновременная активация нейронных клеток приводит к выраженному увеличению синаптической силы между этими клетками. [21] Это часто резюмируют так: «Нейроны, которые срабатывают вместе, соединяются друг с другом. Нейроны, которые срабатывают несинхронно, не могут соединиться».
Правило Хеббиана является одновременно локальным и инкрементным. Для сетей Хопфилда при обучении это реализуется следующим образом. бинарные шаблоны:
где представляет бит i из шаблона .
Если биты, соответствующие нейронам i и j, равны по шаблону , то произведение будет положительным. Это, в свою очередь, положительно скажется на весе. и значения i и j будут стремиться стать равными. Обратное происходит, если биты, соответствующие нейронам i и j, различны.
обучения Правило Сторки
Это правило было введено Амосом Сторки в 1997 году и является одновременно локальным и поэтапным. Сторки также показал, что сеть Хопфилда, обученная по этому правилу, имеет большую пропускную способность, чем соответствующая сеть, обученная по правилу Хеббиана. [22] Весовая матрица нейронной сети-аттрактора [ нужны разъяснения ] Говорят, что он следует правилу обучения Сторки, если он подчиняется:
где является формой локального поля [20] на нейроне i.
Это правило обучения является локальным, поскольку синапсы учитывают только нейроны по бокам. Это правило использует больше информации из шаблонов и весов, чем обобщенное правило Хеббиана, из-за влияния локального поля.
Ложные закономерности [ править ]
Шаблоны, которые сеть использует для обучения (называемые состояниями поиска ), становятся аттракторами системы. Повторные обновления в конечном итоге приведут к сходимости к одному из состояний поиска. Однако иногда сеть сходится к ложным шаблонам (отличным от шаблонов обучения). [23] Энергия в этих ложных узорах также является локальным минимумом. Для каждого сохраненного шаблона x отрицание -x также является ложным шаблоном.
Ложное состояние также может представлять собой линейную комбинацию нечетного числа состояний поиска. Например, при использовании 3 шаблонов , можно получить следующее ложное состояние:
Ложные шаблоны с четным числом состояний не могут существовать, поскольку их сумма может равняться нулю. [23]
Вместимость [ править ]
Емкость сети сетевой модели Хопфилда определяется количеством нейронов и связями внутри данной сети. Следовательно, количество воспоминаний, которые можно сохранить, зависит от нейронов и связей. Кроме того, было показано, что точность восстановления между векторами и узлами составила 0,138 (приблизительно 138 векторов можно вызвать из хранилища на каждые 1000 узлов) (Hertz et al., 1991). Поэтому очевидно, что при попытке сохранить большое количество векторов произойдет много ошибок. Когда модель Хопфилда не запоминает правильный шаблон, возможно, имело место вторжение, поскольку семантически связанные элементы имеют тенденцию сбивать человека с толку, и происходит воспоминание неправильного шаблона. Таким образом, показано, что сетевая модель Хопфилда путает один хранимый элемент с другим при извлечении. Идеальный отзыв и высокая емкость (>0,14) могут быть загружены в сеть с помощью метода обучения Сторки; ЭТАМ, [24] [25] Эксперименты ETAM также проводятся. [26] Позже были разработаны скрытые модели, вдохновленные сетью Хопфилда, чтобы увеличить предел хранения и снизить частоту ошибок поиска, причем некоторые из них были способны к однократному обучению . [27]
Емкость хранилища можно представить как где количество нейронов в сети.
Человеческая память [ править ]
Модель Хопфилда учитывает ассоциативную память посредством включения векторов памяти. Векторы памяти можно слегка использовать, и это приведет к поиску наиболее похожего вектора в сети. Однако мы узнаем, что из-за этого процесса могут произойти вторжения. В ассоциативной памяти сети Хопфилда существуют два типа операций: автоассоциация и гетероассоциация. Первый — когда вектор связан сам с собой, а второй — когда в хранилище связаны два разных вектора. Более того, оба типа операций можно хранить в одной матрице памяти, но только если данная матрица представления не является той или иной из операций, а скорее комбинацией (автоассоциативной и гетероассоциативной) их двух. Важно отметить, что сетевая модель Хопфилда использует то же правило обучения, что и правило обучения Хебба (1949) , которое характеризует обучение как результат усиления весов в случаях активности нейронов.
Риццуто и Кахана (2001) смогли показать, что модель нейронной сети может учитывать повторение и точность воспроизведения за счет включения алгоритма вероятностного обучения. В процессе поиска никакого обучения не происходит. В результате веса сети остаются фиксированными, показывая, что модель способна переключаться с этапа обучения на этап отзыва. Добавив контекстуальный дрейф, они смогли продемонстрировать быстрое забывание, которое происходит в модели Хопфилда во время задачи по запоминанию. Вся сеть способствует изменению активации любого отдельного узла.
Динамическое правило Маккалока и Питтса (1943), которое описывает поведение нейронов, делает это таким образом, что показывает, как активация нескольких нейронов отражается на активации скорости срабатывания нового нейрона и как веса нейронов усиливают синаптические связи между новым активированным нейроном (и теми, которые его активировали). Хопфилд будет использовать динамическое правило Маккаллоха-Питтса, чтобы показать, как поиск возможен в сети Хопфилда. Однако важно отметить, что Хопфилд делал это повторяющимся образом. Хопфилд использовал бы нелинейную функцию активации вместо линейной функции. Таким образом, это привело бы к созданию динамического правила Хопфилда, и благодаря этому Хопфилд смог показать, что с помощью нелинейной функции активации динамическое правило всегда будет изменять значения вектора состояния в направлении одного из сохраненных шаблонов.
сеть Хопфилда Плотная ассоциативная современная память или
Сети Хопфилда [5] [6] представляют собой рекуррентные нейронные сети с динамическими траекториями, сходящимися к состояниям аттрактора с фиксированной точкой и описываемыми энергетической функцией. Состояние каждого модельного нейрона определяется зависящей от времени переменной , который может быть дискретным или непрерывным. Полная модель описывает математику того, как будущее состояние активности каждого нейрона зависит от известной нынешней или предыдущей активности всех нейронов.
В оригинальной модели ассоциативной памяти Хопфилда [5] переменные были бинарными, а динамика описывалась поочередным обновлением состояния нейронов. Энергетическая функция, квадратичная по была определена, а динамика заключалась в изменении активности каждого отдельного нейрона только в том случае, если это приведет к снижению общей энергии системы. Эта же идея была распространена на случай являющаяся непрерывной переменной, представляющей выходные данные нейрона , и является монотонной функцией входного тока. Динамика стала выражаться в виде системы дифференциальных уравнений первого порядка, для которых «энергия» системы всегда уменьшалась. [6] Энергия в непрерывном случае имеет один член, квадратичный по (как в бинарной модели) и второй член, который зависит от функции усиления (функции активации нейрона). Обладая многими желательными свойствами ассоциативной памяти, обе эти классические системы страдают от небольшого объема памяти, который линейно масштабируется с количеством входных функций. [5] Напротив, увеличивая количество параметров в модели так, чтобы между нейронами существовали не только парные, но и взаимодействия более высокого порядка, можно увеличить емкость памяти. [28] [29]
Плотные ассоциативные воспоминания [10] (также известные как современные сети Хопфилда [12] ) являются обобщением классических сетей Хопфилда, которые нарушают соотношение линейного масштабирования между количеством входных объектов и количеством сохраненных воспоминаний. Это достигается за счет введения более сильных нелинейностей (либо в энергетическую функцию, либо в функции активации нейронов), приводящих к сверхлинейности. [10] (даже экспоненциальное [11] ) емкость памяти как функция количества нейронов функций, что фактически увеличивает порядок взаимодействий между нейронами. [28] [29] Сеть по-прежнему требует достаточного количества скрытых нейронов. [13]
Ключевая теоретическая идея, лежащая в основе плотных ассоциативных сетей памяти, заключается в использовании энергетической функции и правила обновления, которые имеют более резкий пик вокруг сохраненных воспоминаний в пространстве конфигураций нейронов по сравнению с классической моделью. [10] как показано при явном моделировании взаимодействий более высокого порядка и последующих энергетических ландшафтов. [29]
Дискретные переменные [ править ]
Простой пример [10] современной сети Хопфилда можно записать в терминах двоичных переменных которые представляют собой активную и неактивен состояние модельного нейрона .
В предельном случае, когда нелинейная энергетическая функция квадратична эти уравнения сводятся к знакомой функции энергии и правилу обновления классической бинарной сети Хопфилда. [5]
Емкость памяти этих сетей можно рассчитать для случайных двоичных шаблонов. Для функции мощности энергии максимальное количество воспоминаний, которые можно сохранить и извлечь из этой сети без ошибок, определяется выражением [10]

Непрерывные переменные [ править ]
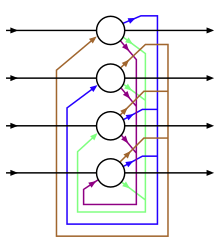
Современные сети Хопфилда или плотные ассоциативные воспоминания лучше всего можно понять в непрерывных переменных и непрерывном времени. [12] [13] Рассмотрим архитектуру сети, показанную на рис.1, и уравнения эволюции состояний нейрона. [13]
| ( 1 ) |
где токи характеристических нейронов обозначены , а токи нейронов памяти обозначаются ( означает скрытые нейроны). Между функциональными нейронами и нейронами памяти нет синаптических связей. Матрица обозначает силу синапсов функционального нейрона к нейрону памяти . Предполагается, что синапсы симметричны, так что одно и то же значение характеризует физический синапс, отличный от нейрона памяти. к функциональному нейрону . Выходы нейронов памяти и нейронов признаков обозначаются и , которые являются нелинейными функциями соответствующих токов. В общем, эти выходные данные могут зависеть от токов всех нейронов в этом слое, так что и . Эти функции активации удобно определить как производные функций Лагранжа для двух групп нейронов.
| ( 2 ) |
Таким образом, конкретный вид уравнений состояний нейрона полностью определяется после задания функций Лагранжа. Наконец, постоянные времени для двух групп нейронов обозначаются через и , — это входной ток в сети, который можно регулировать с помощью представленных данных.

Общие системы нелинейных дифференциальных уравнений могут иметь много сложного поведения, которое может зависеть от выбора нелинейностей и начальных условий. Однако для сетей Хопфилда это не так: динамические траектории всегда сходятся к состоянию аттрактора с фиксированной точкой. Это свойство достигается потому, что эти уравнения специально разработаны так, что в их основе лежит энергетическая функция. [13]
| ( 3 ) |
Члены, сгруппированные в квадратные скобки, представляют собой преобразование Лежандра функции Лагранжа относительно состояний нейронов. Если матрицы Гессе функций Лагранжа положительно полуопределенны, то энергетическая функция гарантированно убывает на динамической траектории [13]
| ( 4 ) |
Это свойство позволяет доказать, что система динамических уравнений, описывающая временную эволюцию активности нейронов, в конечном итоге достигнет состояния аттрактора с фиксированной точкой.
В определенных ситуациях можно предположить, что динамика скрытых нейронов уравновешивается гораздо быстрее по сравнению с динамикой характерных нейронов. . В этом случае стационарное решение второго уравнения системы ( 1 ) можно использовать для выражения токов скрытых единиц через выходы признакных нейронов. Это позволяет свести общую теорию ( 1 ) к эффективной теории только для признаковых нейронов. Полученные в результате эффективные правила обновления и энергии для различных распространенных вариантов функций Лагранжа показаны на рис.2. В случае логарифмической экспоненциальной функции Лагранжа правило обновления (если оно применяется один раз) для состояний характерных нейронов является механизмом внимания. [12] обычно используется во многих современных системах искусственного интеллекта (см. [13] для вывода этого результата из формулировки непрерывного времени).
с классической сетью Хопфилда с непрерывными переменными Связь
Классическая формулировка непрерывных сетей Хопфилда. [6] можно понять [13] как частный предельный случай современных сетей Хопфилда с одним скрытым слоем. Обычно описываются непрерывные сети Хопфилда для нейронов с ступенчатой реакцией. [6] по динамическим уравнениям
| ( 5 ) |
и энергетическая функция
| ( 6 ) |
где , и является обратной функцией активации . Эта модель представляет собой особый предел класса моделей, который называется моделями А. [13] со следующим выбором функций Лагранжа
| ( 7 ) |
что согласно определению ( 2 ) приводит к функциям активации
| ( 8 ) |
Если интегрировать скрытые нейроны, то система уравнений ( 1 ) сводится к уравнениям для признакных нейронов ( 5 ) с , а общее выражение для энергии ( 3 ) сводится к эффективной энергии
| ( 9 ) |
Хотя первые два члена в уравнении ( 6 ) такие же, как и в уравнении ( 9 ), третьи члены внешне выглядят иначе. В уравнении ( 9 ) это преобразование Лежандра лагранжиана для характерных нейронов, а в ( 6 ) третий член представляет собой интеграл обратной функции активации. Тем не менее, эти два выражения на самом деле эквивалентны, поскольку производные функции и ее преобразования Лежандра являются обратными функциями друг друга. Самый простой способ увидеть, что эти два термина явно равны, — это дифференцировать каждый из них по . Результаты этих дифференцирований для обоих выражений равны . Таким образом, два выражения равны с точностью до аддитивной константы. Это завершает доказательство [13] что классическая сеть Хопфилда с непрерывными состояниями [6] является частным предельным случаем современной сети Хопфилда ( 1 ) с энергией ( 3 ).
современной сети формулировка Общая Хопфилда

Биологические нейронные сети обладают большой степенью гетерогенности в отношении разных типов клеток. В этом разделе описывается математическая модель полностью связной современной сети Хопфилда, предполагающая крайнюю степень неоднородности: каждый нейрон уникален. [30] В частности, энергетическая функция и соответствующие динамические уравнения описываются в предположении, что каждый нейрон имеет свою собственную функцию активации и кинетическую шкалу времени. Предполагается, что сеть полностью связна, так что каждый нейрон связан с каждым другим нейроном с помощью симметричной матрицы весов. , индексы и перечислить разные нейроны в сети, см. рис.3. Самый простой способ математически сформулировать эту проблему — определить архитектуру через функцию Лагранжа. это зависит от активности всех нейронов в сети. Функция активации для каждого нейрона определяется как частная производная лагранжиана по активности этого нейрона.
| ( 10 ) |
С биологической точки зрения можно подумать о как аксональный выход нейрона . В простейшем случае, когда лагранжиан аддитивен для разных нейронов, это определение приводит к активации, которая является нелинейной функцией активности этого нейрона. Для неаддитивных лагранжианов эта функция активации может зависеть от активности группы нейронов. Например, он может содержать контрастную (softmax) или разделительную нормализацию. Динамические уравнения, описывающие временную эволюцию данного нейрона, имеют вид [30]
| ( 11 ) |
Это уравнение принадлежит к классу моделей, называемых в нейробиологии моделями скорости стрельбы. Каждый нейрон собирает выходы аксонов от всех нейронов, взвешивает их с помощью синаптических коэффициентов и производит свою собственную, зависящую от времени активность . Временная эволюция имеет постоянную времени , которые в общем случае могут быть разными для каждого нейрона. Эта сеть имеет глобальную энергетическую функцию. [30]
| ( 12 ) |
где первые два члена представляют собой преобразование Лежандра функции Лагранжа относительно токов нейронов . Производная по времени этой энергетической функции может быть вычислена на динамических траекториях, ведущих к (см. [30] подробности)
| ( 13 ) |
Последний знак неравенства имеет место при условии, что матрица (или его симметричная часть) положительно полуопределена. Если вдобавок к этому энергетическая функция ограничена снизу, то нелинейные динамические уравнения гарантированно сходятся к состоянию аттрактора с неподвижной точкой. Преимущество формулирования этой сети в терминах функций Лагранжа состоит в том, что она позволяет легко экспериментировать с различным выбором функций активации и различным архитектурным расположением нейронов. Для всех этих гибких вариантов условия сходимости определяются свойствами матрицы и существование нижней границы энергетической функции.
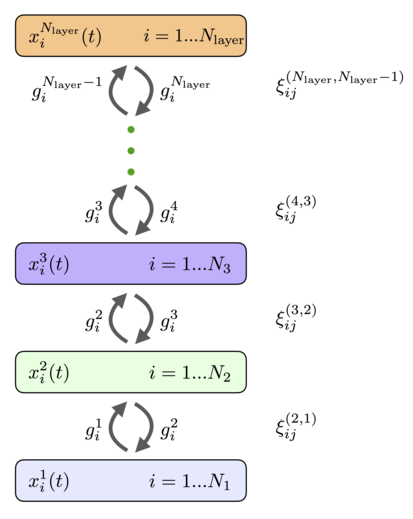
памяти ассоциативная Иерархическая сеть
Нейроны могут быть организованы в слои так, чтобы каждый нейрон в данном слое имел одинаковую функцию активации и одинаковую динамическую шкалу времени. Если предположить, что между нейронами внутри слоя нет горизонтальных связей (латеральных связей) и нет связей с пропуском слоев, то общая полносвязная сеть ( 11 ), ( 12 ) сводится к архитектуре, показанной на рис.4. Он имеет слои рекуррентно связанных нейронов с состояниями, описываемыми непрерывными переменными и функции активации , индекс перечисляет слои сети и индексирует перечисляет отдельные нейроны в этом слое. Функции активации могут зависеть от активности всех нейронов слоя. Каждый слой может иметь разное количество нейронов. . Эти нейроны рекуррентно связаны с нейронами предыдущего и последующих слоев. Матрицы весов, соединяющие нейроны в слоях и обозначаются (порядок верхних индексов весов такой же, как порядок нижних индексов, в примере выше это означает, что индекс перечисляет нейроны в слое и индекс перечисляет нейроны в слое ). Веса прямой связи и веса обратной связи равны. Динамические уравнения состояний нейронов можно записать в виде [30]
| ( 14 ) |
с граничными условиями
| ( 15 ) |
Основное отличие этих уравнений от уравнений обычных сетей прямого распространения заключается в наличии второго члена, который отвечает за обратную связь с более высокими уровнями. Эти нисходящие сигналы помогают нейронам нижних слоев принять решение о своей реакции на предъявленные стимулы. Следуя общему рецепту, удобно ввести функцию Лагранжа для -й скрытый слой, который зависит от активности всех нейронов этого слоя. [30] Функции активации в этом слое можно определить как частные производные лагранжиана
| ( 16 ) |
С этими определениями функция энергии (Ляпунова) определяется выражением [30]
| ( 17 ) |
Если функции Лагранжа или, что то же самое, функции активации выбраны таким образом, что гессиан для каждого слоя является положительно полуопределенным, а общая энергия ограничена снизу, эта система гарантированно сходится к состоянию аттрактора с фиксированной точкой. Производная по времени этой энергетической функции определяется выражением [30]
| ( 18 ) |
Таким образом, иерархическая слоистая сеть действительно является сетью-аттрактором с глобальной энергетической функцией. Эта сеть описывается иерархическим набором синаптических весов, которые можно изучить для каждой конкретной проблемы.
См. также [ править ]
- Ассоциативная память (значения)
- Автоассоциативная память
- Машина Больцмана - похожа на сеть Хопфилда, но вместо градиентного спуска использует отожженную выборку Гиббса.
- Модель динамических систем познания
- Модель Изинга
- Теория Хебба
Ссылки [ править ]
- ^ Браш, Стивен Г. (1967). «История модели Ленца-Изинга». Обзоры современной физики . 39 (4): 883–893. Бибкод : 1967РвМП...39..883Б . дои : 10.1103/RevModPhys.39.883 .
- ^ Jump up to: Перейти обратно: а б Амари, Сюн-Ичи (1972). «Обучение шаблонам и последовательностям шаблонов с помощью самоорганизующихся сетей пороговых элементов». IEEE-транзакции . С (21): 1197–1206.
- ^ Шмидхубер, Юрген (2022). «Аннотированная история современного искусственного интеллекта и глубокого обучения». arXiv : 2212.11279 [ cs.NE ].
- ^ Jump up to: Перейти обратно: а б Литтл, Вашингтон (1974). «Существование постоянных состояний в мозге». Математические биологические науки . 19 (1–2): 101–120. дои : 10.1016/0025-5564(74)90031-5 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час Хопфилд, Джей-Джей (1982). «Нейронные сети и физические системы с возникающими коллективными вычислительными способностями» . Труды Национальной академии наук . 79 (8): 2554–2558. Бибкод : 1982PNAS...79.2554H . дои : 10.1073/pnas.79.8.2554 . ПМЦ 346238 . ПМИД 6953413 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час Хопфилд, Джей-Джей (1984). «Нейроны с дифференцированной реакцией обладают коллективными вычислительными свойствами, подобными свойствам нейронов с двумя состояниями» . Труды Национальной академии наук . 81 (10): 3088–3092. Бибкод : 1984PNAS...81.3088H . дои : 10.1073/pnas.81.10.3088 . ПМЦ 345226 . ПМИД 6587342 .
- ^ Амит, диджей (1992). Моделирование функций мозга: мир нейронных сетей-аттракторов . Издательство Кембриджского университета. ISBN 978-0-521-42124-9 .
- ^ Роллс, Эдмунд Т. (2016). Кора головного мозга: принципы работы . Издательство Оксфордского университета. ISBN 978-0-19-878485-2 .
- ^ Глаубер, Рой Дж. (февраль 1963 г.). «Рой Дж. Глаубер «Зависящая от времени статистика модели Изинга» » . Журнал математической физики . 4 (2): 294–307. дои : 10.1063/1.1703954 . Проверено 21 марта 2021 г.
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж Кротов Дмитрий; Хопфилд, Джон (2016). «Плотная ассоциативная память для распознавания образов». Нейронные системы обработки информации . 29 : 1172–1180. arXiv : 1606.01164 .
- ^ Jump up to: Перейти обратно: а б с д Мете, Демирджигил; и др. (2017). «О модели ассоциативной памяти с огромной емкостью» . Журнал статистической физики . 168 (2): 288–299. arXiv : 1702.01929 . Бибкод : 2017JSP...168..288D . дои : 10.1007/s10955-017-1806-y . S2CID 119317128 .
- ^ Jump up to: Перейти обратно: а б с д и Рамзауэр, Хуберт; и др. (2021). «Hopfield Networks — это все, что вам нужно». Международная конференция по обучению представлений . arXiv : 2008.02217 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к Кротов Дмитрий; Хопфилд, Джон (2021). «Большая ассоциативная проблема памяти в нейробиологии и машинном обучении». Международная конференция по обучению представлений . arXiv : 2008.06996 .
- ^ Хопфилд, Джей-Джей (1982). «Нейронные сети и физические системы с возникающими коллективными вычислительными способностями» . Труды Национальной академии наук . 79 (8): 2554–2558. Бибкод : 1982PNAS...79.2554H . дои : 10.1073/pnas.79.8.2554 . ПМЦ 346238 . ПМИД 6953413 .
- ^ Маккей, Дэвид Дж. К. (2003). «42. Сети Хопфилда». Теория информации, логический вывод и алгоритмы обучения . Издательство Кембриджского университета . п. 508 . ISBN 978-0521642989 .
Это доказательство сходимости решающим образом зависит от того факта, что соединения сети Хопфилда симметричны . Это также зависит от асинхронного выполнения обновлений.
- ^ Jump up to: Перейти обратно: а б с Брук, Дж. (октябрь 1990 г.). «О свойствах сходимости модели Хопфилда» . Учеб. ИИЭЭ . 78 (10): 1579–85. дои : 10.1109/5.58341 .
- ^ Jump up to: Перейти обратно: а б с д и ж Уйкан, З. (сентябрь 2020 г.). «О принципе работы нейронных сетей Хопфилда и их эквивалентности GADIA в оптимизации» . Транзакции IEEE в нейронных сетях и системах обучения . 31 (9): 3294–3304. дои : 10.1109/TNNLS.2019.2940920 . ПМИД 31603804 . S2CID 204331533 .
- ^ Уйкан, З. (март 2021 г.). «Минимизация/максимизация теней и сложные нейронные сети Хопфилда» . Транзакции IEEE в нейронных сетях и системах обучения . 32 (3): 1096–1109. дои : 10.1109/TNNLS.2020.2980237 . ПМИД 32310787 . S2CID 216047831 .
- ^ Хопфилд, Джей-Джей; Танк, Д.В. (1985). «Нейронные вычисления решений в задачах оптимизации». Биологическая кибернетика . 52 (3): 141–6. дои : 10.1007/BF00339943 . ПМИД 4027280 . S2CID 36483354 .
- ^ Jump up to: Перейти обратно: а б Сторки, Эй Джей; Валабрег, Р. (1999). «Тассейны привлекательности нового правила обучения Хопфилда». Нейронные сети . 12 (6): 869–876. CiteSeerX 10.1.1.19.4681 . дои : 10.1016/S0893-6080(99)00038-6 . ПМИД 12662662 .
- ^ Хебб 1949
- ^ Сторки, Амос (1997). «Увеличение пропускной способности сети Хопфилда без ущерба для функциональности». Искусственные нейронные сети – ICANN'97 . Конспекты лекций по информатике. Том. 1327. Спрингер. стр. 451–6. CiteSeerX 10.1.1.33.103 . дои : 10.1007/BFb0020196 . ISBN 978-3-540-69620-9 .
- ^ Jump up to: Перейти обратно: а б Герц 1991 г.
- ^ Лиу, К.-Ю.; Лин, С.-Л. (2006). «Конечная загрузка памяти в волосатых нейронах» (PDF) . Естественные вычисления . 5 (1): 15–42. дои : 10.1007/s11047-004-5490-x . S2CID 35025761 .
- ^ Лиу, К.-Ю.; Юань, С.-К. (1999). «Ошибочноустойчивая ассоциативная память». Биологическая кибернетика . 81 (4): 331–342. дои : 10.1007/s004220050566 . ПМИД 10541936 . S2CID 6168346 .
- ^ Юань, С.-К. (июнь 1997 г.). Расширение бассейнов притяжения ассоциативной памяти (Магистерская диссертация). Национальный Тайваньский университет. 991010725609704786.
- ^ АБУДИБ, Ала; ГРИПОН, Винсент; Цзян, Сяорань (2014). «Исследование алгоритмов поиска разреженных сообщений в сетях нейронных клик» . COGNITIVE 2014: 6-я Международная конференция по передовым когнитивным технологиям и приложениям . стр. 140–6. arXiv : 1308.4506 . Бибкод : 2013arXiv1308.4506A .
- ^ Jump up to: Перейти обратно: а б Хорн, Д; Ашер, М. (1988). «Мощности многосвязных моделей памяти» . Дж. Физ. Франция . 49 (3): 389–395. doi : 10.1051/jphys:01988004903038900 .
- ^ Jump up to: Перейти обратно: а б с Бернс, Томас; Фукай, Томоки (2023). «Симплициальные сети Хопфилда» . Международная конференция по обучению представлений . 11 . arXiv : 2305.05179 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я Кротов, Дмитрий (2021). «Иерархическая ассоциативная память». arXiv : 2107.06446 [ cs.NE ].
- Хебб, Д.О. (2005) [1949]. Организация поведения: нейропсихологическая теория . Психология Пресс. ISBN 978-1-135-63190-1 .
- Герц, Джон А. (2018) [1991]. Введение в теорию нейронных вычислений . ЦРК Пресс. ISBN 978-0-429-96821-1 .
- Маккалок, штат Вашингтон; Питтс, WH (1943). «Логическое исчисление идей, имманентных нервной деятельности». Вестник математической биофизики . 5 (4): 115–133. дои : 10.1007/BF02478259 .
- Полин, С.М.; Кахана, MJ (2008). «Поиск в памяти и нейронное представление контекста» . Тенденции в когнитивных науках . 12 (1): 24–30. дои : 10.1016/j.tics.2007.10.010 . ПМЦ 2839453 . ПМИД 18069046 .
- Риццуто, Д.С.; Кахана, MJ (2001). «Автоассоциативная нейронная сетевая модель парно-ассоциированного обучения». Нейронные вычисления . 13 (9): 2075–2092. CiteSeerX 10.1.1.45.7929 . дои : 10.1162/089976601750399317 . ПМИД 11516358 . S2CID 7675117 .
- Крузе, Рудольф; Боргельт, Кристиан; Клавонн, Фрэнк; Мовес, Кристиан; Штайнбрехер, Матиас; Хелд, Паскаль (2013). Вычислительный интеллект: методологическое введение . Спрингер. ISBN 978-1-4471-5013-8 .
Внешние ссылки [ править ]
- Рохас, Рауль (12 июля 1996 г.). «13. Модель Хопфилда» (PDF) . Нейронные сети – систематическое введение . Спрингер. ISBN 978-3-540-60505-8 .
- Сеть Хопфилда Javascript
- Задача коммивояжера. Архивировано 30 мая 2015 г. в Wayback Machine - JAVA-апплет нейронной сети Хопфилда.
- Хопфилд, Джон (2007). «Сеть Хопфилда» . Схоларпедия . 2 (5): 1977. Бибкод : 2007SchpJ...2.1977H . doi : 10.4249/scholarpedia.1977 .
- Флетчер, Тристан. «Обучение сети Хопфилда с использованием детерминированных скрытых переменных» (PDF) (учебник). Архивировано из оригинала (PDF) 5 октября 2011 г.
























































![{\displaystyle V_{i}^{(t+1)}=Sign{\bigg [}\sum \limits _{\mu =1}^{N_{\text{mem}}}{\bigg (}F {\Big (}\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}-F {\Big (}-\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}{ \бигг )}{\бигг ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f610dc9c7b006debf54cab514e242c9dbc1ac72)




















![{\displaystyle E(t)={\Big [}\sum \limits _{i=1}^{N_{f}}(x_{i}-I_{i})g_{i}-L_{x} {\Big ]}+{\Big [}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }f_{\mu }-L_{h}{\Big ]}- \sum \limits _{\mu,i}f_{\mu }\xi _{\mu i}g_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49e7d96e213a43700492bcdcc56832be110a2f0d)







































![{\displaystyle E=\sum \limits _{A=1}^{N_{\text{layer}}}{\Big [}\sum \limits _{i=1}^{N_{A}}x_{ i}^{A}g_{i}^{A}-L^{A}{\Big ]}-\sum \limits _{A=1}^{N_{\text{layer}}-1}\ sum \limits _{i=1}^{N_{A+1}}\sum \limits _{j=1}^{N_{A}}g_{i}^{A+1}\xi _{ij }^{(A+1,A)}g_{j}^{A}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087774b10637a0e122dd10a4f8e5893df2aca372)
