Контактный процесс (математика)

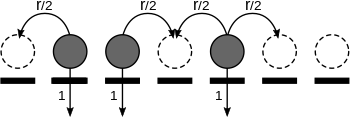
Контактный процесс (на одномерной решетке): активные сайты обозначены серыми кружками, а неактивные сайты - пунктирными кружками. Активные сайты могут активировать неактивные сайты по обе стороны от них со скоростью r /2 или становиться неактивными со скоростью 1.

Контактный процесс — это стохастический процесс, используемый для моделирования роста населения на множестве участков. $S$ графа , в котором занятые сайты освобождаются с постоянной скоростью, а свободные сайты заполняются со скоростью, пропорциональной количеству занятых соседних сайтов. Поэтому, если мы обозначим через $\lambda$ константа пропорциональности, каждый сайт остается занятым в течение случайного периода времени, который экспоненциально распределяется параметром 1 и помещает потомков в каждый свободный соседний сайт во время событий процесса Пуассона параметра $\lambda$ в этот период. Все процессы независимы друг от друга и в произвольный период времени сайты остаются занятыми. Контактный процесс также можно интерпретировать как модель распространения инфекции путем представление о частицах как о бактериях, распространяющихся по индивидуумам, расположенным в местах $S$, занятые места соответствуют зараженным особям, а свободные – здоровым.

Основная интересующая нас величина — это количество частиц в процессе, скажем $N_{t}$, в первой интерпретации, что соответствует количеству зараженных сайтов во второй. Таким образом, процесс выживает , когда число частиц положительно во все времена, что соответствует случаю, когда во втором процессе всегда есть инфицированные особи. Для любого бесконечного графа $S$ существует положительное и конечное критическое значение $\lambda _{c}$ так что если $\lambda >\lambda _{c}$ то выживание процесса, начиная с конечного числа частиц, происходит с положительной вероятностью, а если $\lambda <\lambda _{c}$ их исчезновение почти неизбежно. Обратите внимание, что в соответствии с доведением до абсурда и теоремой о бесконечных обезьянах выживание процесса эквивалентно $N_{t}\to \infty$, как $t\to \infty$, тогда как угасание эквивалентно $N_{t}\to 0$, как $t\to \infty$, и поэтому естественно задаться вопросом о скорости, с которой $N_{t}\to \infty$ когда процесс выживет.

Математическое определение

Если состояние процесса в момент времени $t$ является $\xi _{t}$, затем сайт $x$ в $S$ занято, скажем, частицей, если $\xi _{t}(x)=1$ и вакантным, если $\xi _{t}(x)=0$. Контактный процесс представляет собой непрерывный марковский процесс с пространством состояний. $\{0,1\}^{S}$, где $S$ — конечный или счетный граф , обычно $\mathbb {Z} ^{d}$и частный случай взаимодействующей системы частиц .Более конкретно, динамика основного контактного процесса определяется следующими темпами перехода: на месте $x$,

$1\rightarrow 0\quad {\text{at rate }}1,$

$0\rightarrow 1\quad {\text{at rate }}\lambda \sum _{y\,:\,y\,\sim \,x}\xi _{t}(y),$

где сумма по всем соседям $y$ из $x$ в $S$. Это означает, что каждый сайт ожидает экспоненциальное время с соответствующей скоростью, а затем переключается (так что 0 становится 1 и наоборот).

Подключение к перколяции

Контактный процесс — это случайный процесс , тесно связанный с теорией перколяции . Тед Харрис (1974) отметил, что процесс контакта $\mathbb {Z} ^{d}$ когда заражения и выздоровления могут происходить только в дискретные моменты времени $\{1,2,\ldots ,\}$ соответствует поэтапной перколяции связей на графе, полученном ориентацией каждого ребра $\mathbb {Z} ^{d+1}$ в сторону увеличения координаты.

Закон больших чисел о целых числах

Закон больших чисел для числа частиц в процессе в целых числах неформально означает, что для всех больших $t$, $N_{t}$ приблизительно равно $ct$ для некоторой положительной константы $c=c(\lambda )$. Харрис (1974) доказал, что если процесс сохраняется, то скорость роста $N_{t}$ максимально и по крайней мере линейна во времени. Слабый закон больших чисел (что процесс сходится по вероятности ) был показан Дарреттом (1980). Несколько лет спустя Дарретт и Гриффит (1983) усовершенствовали этот закон до строгого закона больших чисел, обеспечив почти уверенную сходимость процесса.

Вымереть при критичности

Контактные процессы на всех целочисленных решетках почти наверняка затухают при критическом значении.

Гипотеза Дарретта и центральная предельная теорема

Дарретт выдвинул гипотезу В обзорных статьях и конспектах лекций в 1980-х и начале 1990-х годов относительно центральной предельной теоремы для контактного процесса Харриса, а именно. что, если процесс выживет, то для всех крупных $t$, $N_{t}$ равно $ct$ и ошибка равна $\sigma {\sqrt {t}}$ умножается на (случайную) ошибку, распределенную в соответствии со стандартным распределением Гаусса .

Гипотеза Дарретта оказалась верной для другого значения $\sigma$ как было доказано в 2018 году.

Дальнейшее чтение

• Дарретт, Ричард (1980). «О росте одномерных контактных процессов» . Анналы вероятности . 8 (5): 890–907. дои : 10.1214/aop/1176994619 .
• Дарретт, Ричард ; Дэвид Гриффит (1983). «Сверхкритические контактные процессы на Z» . Анналы вероятности . 11 (1): 1–15. дои : 10.1214/aop/1176993655 .
• Гриммет, Джеффри (1999), Перколяция , Спрингер
• Лиггетт, Томас М. (1985). Взаимодействующие системы частиц . Нью-Йорк: Springer Verlag. ISBN  978-0-387-96069-2 .
• Томас М. Лиггетт , «Стохастические взаимодействующие системы: процессы контакта, избирателя и исключения», Springer-Verlag, 1999.