Гауссов процесс

В теории вероятностей и статистике гауссов процесс — это случайный процесс (набор случайных величин, индексированных по времени или пространству), такой, что каждый конечный набор этих случайных величин имеет многомерное нормальное распределение . Распределение гауссовского процесса — это совместное распределение всех этих (бесконечно многих) случайных величин и, как таковое, распределение по функциям с непрерывной областью определения, например, во времени или пространстве.

Концепция гауссовских процессов названа в честь Карла Фридриха Гаусса , поскольку в ее основе лежит понятие гауссовского распределения ( нормального распределения ). Гауссовские процессы можно рассматривать как бесконечномерное обобщение многомерных нормальных распределений.

Гауссовы процессы полезны в статистическом моделировании , поскольку они извлекают выгоду из свойств, унаследованных от нормального распределения. Например, если случайный процесс моделируется как гауссовский процесс, распределения различных производных величин можно получить явно. К таким величинам относятся среднее значение процесса за определенный период времени и ошибка оценки среднего значения с использованием выборочных значений за небольшой набор периодов времени. Хотя точные модели часто плохо масштабируются по мере увеличения объема данных, несколько методов аппроксимации было разработано , которые часто сохраняют хорошую точность, резко сокращая время вычислений.

Определение

Непрерывный во времени случайный процесс $\left\{X_{t};t\in T\right\}$ является гауссовым тогда и только тогда, когда для любого конечного индексов набора $t_{1},\ldots ,t_{k}$ в наборе индексов $T$

$$\mathbf {X} _{t_{1},\ldots ,t_{k}}=(X_{t_{1}},\ldots ,X_{t_{k}})$$

— многомерная гауссова случайная величина . Это то же самое, что сказать, что каждая линейная комбинация $(X_{t_{1}},\ldots ,X_{t_{k}})$ имеет одномерное нормальное (или гауссово) распределение.

Используя характеристические функции случайных величин с $i$ обозначая мнимую единицу такую, что $i^{2}=-1$, свойство Гаусса можно сформулировать следующим образом: $\left\{X_{t};t\in T\right\}$ является гауссовым тогда и только тогда, когда для любого конечного набора индексов $t_{1},\ldots ,t_{k}$, есть действительные значения $\sigma _{\ell j}$, $\mu _{\ell }$ с $\sigma _{jj}>0$ такая, что для всех имеет место равенство $s_{1},s_{2},\ldots ,s_{k}\in \mathbb {R}$,

$${\mathbb {E} }\left[\exp \left(i\sum _{\ell =1}^{k}s_{\ell }\,\mathbf {X} _{t_{\ell }}\right)\right]=\exp \left(-{\tfrac {1}{2}}\sum _{\ell ,j}\sigma _{\ell j}s_{\ell }s_{j}+i\sum _{\ell }\mu _{\ell }s_{\ell }\right),$$

или ${\mathbb {E} }\left[{\mathrm {e} }^{i\,\mathbf {s} \,(\mathbf {X} _{t}-\mathbf {\mu } )}\right]={\mathrm {e} }^{-\mathbf {s} \,\sigma \,\mathbf {s} /2}$. Числа $\sigma _{\ell j}$ и $\mu _{\ell }$ Можно показать, что это ковариации и средние значения переменных в процессе.

Дисперсия

Дисперсия гауссовского процесса конечна в любой момент времени. $t$, формально $$\operatorname {var} [X(t)]={\mathbb {E} }\left[\left|X(t)-\operatorname {E} [X(t)]\right|^{2}\right]<\infty \quad {\text{for all }}t\in T.$$

Стационарность

Для общих случайных процессов стационарность в строгом смысле подразумевает стационарность в широком смысле , но не каждый стационарный случайный процесс в широком смысле является стационарным в строгом смысле. Однако для гауссовского случайного процесса эти две концепции эквивалентны.

Гауссов случайный процесс является стационарным в строгом смысле тогда и только тогда, когда он стационарен в широком смысле.

Пример

Существует явное представление для стационарных гауссовских процессов. Простой пример такого представления:

$$X_{t}=\cos(at)\,\xi _{1}+\sin(at)\,\xi _{2}$$

где $\xi _{1}$ и $\xi _{2}$ являются независимыми случайными величинами со стандартным нормальным распределением .

Ковариационные функции

Основная статья: Ковариационная функция

Дополнительная информация: Вариограмма.

Ключевым фактом гауссовских процессов является то, что они могут быть полностью определены их статистикой второго порядка. Таким образом, если предполагается, что гауссовский процесс имеет нулевое среднее, определение функции ковариации полностью определяет поведение процесса. Важно отметить, что неотрицательная определенность этой функции позволяет ее спектральное разложение с использованием расширения Карунена-Лоэва . процесса Основными аспектами, которые можно определить с помощью ковариационной функции, являются стационарность , изотропность , гладкость и периодичность .

Стационарность относится к поведению процесса в отношении разделения любых двух точек. $x$ и $x'$. Если процесс стационарен, ковариационная функция зависит только от $x-x'$. Например, процесс Орнштейна–Уленбека стационарен.

Если процесс зависит только от $|x-x'|$, евклидово расстояние (не направление) между $x$ и $x'$, то процесс считается изотропным. считается процесс, одновременно стационарный и изотропный Однородным ; на практике эти свойства отражают различия (вернее, их отсутствие) в поведении процесса в зависимости от местоположения наблюдателя.

В конечном итоге гауссовские процессы переводятся как принятие априорных значений функций, и гладкость этих априорных значений может быть вызвана функцией ковариации. Если мы ожидаем, что для «близких» входных точек $x$ и $x'$ соответствующие им выходные точки $y$ и $y'$ быть также «рядом», то присутствует предположение о непрерывности. Если мы хотим учесть значительное смещение, мы можем выбрать более грубую ковариационную функцию. Крайними примерами такого поведения являются ковариационная функция Орнштейна – Уленбека и квадратичная экспонента, где первая никогда не дифференцируема, а вторая бесконечно дифференцируема.

Периодичность означает создание периодических закономерностей в поведении процесса. Формально это достигается путем отображения входных данных $x$ в двумерный вектор $u(x)=\left(\cos(x),\sin(x)\right)$.

Обычные ковариационные функции

Влияние выбора разных ядер на распределение априорной функции гауссовского процесса. Слева — квадрат экспоненциального ядра. Середина – броуновская. Справа квадратично.

Существует ряд общих ковариационных функций:

• Постоянный : $K_{\operatorname {C} }(x,x')=C$
• Линейный: $K_{\operatorname {L} }(x,x')=x^{\mathsf {T}}x'$
• белый гауссов шум: $K_{\operatorname {GN} }(x,x')=\sigma ^{2}\delta _{x,x'}$
• Квадратная экспонента: $K_{\operatorname {SE} }(x,x')=\exp \left(-{\tfrac {|d|^{2}}{2\ell ^{2}}}\right)$
• Орнштейн-Уленбек: $K_{\operatorname {OU} }(x,x')=\exp \left(-{\tfrac {|d|}{\ell }}\right)$
• Мать: $K_{\operatorname {Matern} }(x,x')={\tfrac {2^{1-\nu }}{\Gamma (\nu )}}\left({\tfrac {{\sqrt {2\nu }}|d|}{\ell }}\right)^{\nu }K_{\nu }\left({\tfrac {{\sqrt {2\nu }}|d|}{\ell }}\right)$
• Периодический: $K_{\operatorname {P} }(x,x')=\exp \left(-{\tfrac {2}{\ell ^{2}}}\sin ^{2}(d/2)\right)$
• Рациональный квадратик: $K_{\operatorname {RQ} }(x,x')=\left(1+|d|^{2}\right)^{-\alpha },\quad \alpha \geq 0$

Здесь $d=x-x'$. Параметр $\ell$ — характерный масштаб процесса (практически «насколько близко» две точки $x$ и $x'$ должны существенно влиять друг на друга), $\delta$ это дельта Кронекера и $\sigma$ стандартное отклонение шумовых флуктуаций. Более того, $K_{\nu }$ — Бесселя модифицированная функция порядка $\nu$ и $\Gamma (\nu )$ гамма -функция оценивается при $\nu$. Важно отметить, что сложную ковариационную функцию можно определить как линейную комбинацию других более простых ковариационных функций, чтобы учесть различные представления о имеющемся наборе данных.

Результаты вывода зависят от значений гиперпараметров. $\theta$ (например $\ell$ и $\sigma$), определяющий поведение модели. Популярный выбор для $\theta$ состоит в том, чтобы обеспечить максимальные апостериорные его (MAP) оценки с некоторыми выбранными априорными значениями. Если априор очень близок к однородному, это то же самое, что максимизировать предельную вероятность процесса; маргинализация, выполняемая по наблюдаемым значениям процесса $y$. Этот подход также известен как метод максимального правдоподобия II , максимизация доказательств или эмпирический Байес .

Непрерывность

Для гауссовского процесса непрерывность по вероятности эквивалентна среднеквадратической непрерывности , и непрерывность с вероятностью единица эквивалентна непрерывности выборки . Последнее предполагает, но не подразумевает, непрерывность вероятности.Непрерывность вероятности имеет место тогда и только тогда, когда среднее значение и автоковариация являются непрерывными функциями. Напротив, непрерывность выборки была сложной задачей даже для стационарных гауссовских процессов (как, вероятно, впервые заметил Андрей Колмогоров ), и еще более сложной задачей для более общих процессов. Как обычно, под выборочным непрерывным процессом понимают процесс, допускающий выборочную непрерывную модификацию .

Стационарный корпус

Для стационарного гауссовского процесса $X=(X_{t})_{t\in \mathbb {R} },$ некоторые условия в его спектре достаточны для непрерывности образца, но не являются необходимыми. Необходимое и достаточное условие, иногда называемое теоремой Дадли – Фернике, включает функцию $\sigma$ определяется $$\sigma (h)={\sqrt {{\mathbb {E} }{\big [}X(t+h)-X(t){\big ]}^{2}}}$$(правая часть не зависит от $t$ из-за стационарности). Непрерывность $X$ по вероятности эквивалентно непрерывности $\sigma$ в $0.$ При сближении $\sigma (h)$ к $0$ (как $h\to 0$) слишком медленный, непрерывность выборки $X$ может потерпеть неудачу. Имеет значение сходимость следующих интегралов: $$I(\sigma )=\int _{0}^{1}{\frac {\sigma (h)}{h{\sqrt {\log(1/h)}}}}\,dh=\int _{0}^{\infty }2\sigma (e^{-x^{2}})\,dx,$$эти два интеграла равны согласно интегрированию путем замены ${\textstyle h=e^{-x^{2}},}$ ${\textstyle x={\sqrt {\log(1/h)}}.}$ Первый подынтегральный оператор не обязательно должен быть ограничен как $h\to 0+,$ таким образом, интеграл может сходиться ( $I(\sigma )<\infty$) или расходятся ( $I(\sigma )=\infty$). Взяв для примера ${\textstyle \sigma (e^{-x^{2}})={\tfrac {1}{x^{a}}}}$ для больших $x,$ то есть, ${\textstyle \sigma (h)=(\log(1/h))^{-a/2}}$ для маленьких $h,$ получается $I(\sigma )<\infty$ когда $a>1,$ и $I(\sigma )=\infty$ когда $0<a\leq 1.$В этих двух случаях функция $\sigma$ увеличивается на $[0,\infty ),$ но в целом это не так. Более того, условие

(*) существует $\varepsilon >0$ такой, что $\sigma$ является монотонным на $[0,\varepsilon ]$

не следует из непрерывности $\sigma$ и очевидные отношения $\sigma (h)\geq 0$ (для всех $h$) и $\sigma (0)=0.$

Теорема Пусть 1. $\sigma$ быть непрерывным и удовлетворять (*) . Тогда условие $I(\sigma )<\infty$ необходимо и достаточно для обеспечения непрерывности выборки $X.$

Немного истории. Достаточность была объявлена ​​Ксавье Ферником в 1964 году, но первое доказательство было опубликовано Ричардом М. Дадли в 1967 году. Необходимость доказали Майкл Б. Маркус и Лоуренс Шепп в 1970 году.

Существуют образцы непрерывных процессов $X$ такой, что $I(\sigma )=\infty ;$ они нарушают условие (*) . Пример, найденный Маркусом и Шеппом представляет собой случайный лакунарный ряд Фурье $$X_{t}=\sum _{n=1}^{\infty }c_{n}(\xi _{n}\cos \lambda _{n}t+\eta _{n}\sin \lambda _{n}t),$$где $\xi _{1},\eta _{1},\xi _{2},\eta _{2},\dots$ являются независимыми случайными величинами со стандартным нормальным распределением ; частоты $0<\lambda _{1}<\lambda _{2}<\dots$ являются быстрорастущей последовательностью; и коэффициенты $c_{n}>0$ удовлетворить ${\textstyle \sum _{n}c_{n}<\infty .}$ Последнее соотношение подразумевает

${\textstyle {\mathbb {E} }\sum _{n}c_{n}(|\xi _{n}|+|\eta _{n}|)=\sum _{n}c_{n}{\mathbb {E} }[|\xi _{n}|+|\eta _{n}|]={\text{const}}\cdot \sum _{n}c_{n}<\infty ,}$

откуда ${\textstyle \sum _{n}c_{n}(|\xi _{n}|+|\eta _{n}|)<\infty }$ почти наверняка, что почти наверняка обеспечивает равномерную сходимость ряда Фурье и выборочную непрерывность $X.$

Автокорреляция случайного лакунарного ряда Фурье

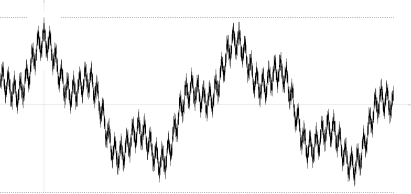
Его автоковариационная функция $${\mathbb {E} }[X_{t}X_{t+h}]=\sum _{n=1}^{\infty }c_{n}^{2}\cos \lambda _{n}h$$нигде не монотонна (см. рисунок), как и соответствующая функция $\sigma ,$$$\sigma (h)={\sqrt {2{\mathbb {E} }[X_{t}X_{t}]-2{\mathbb {E} }[X_{t}X_{t+h}]}}=2{\sqrt {\sum _{n=1}^{\infty }c_{n}^{2}\sin ^{2}{\frac {\lambda _{n}h}{2}}}}.$$

Броуновское движение как интеграл гауссовских процессов

Винеровский процесс (также известный как броуновское движение) является интегралом обобщенного гауссовского процесса белого шума . Он не стационарен , но имеет стационарные приращения .

Процесс Орнштейна – Уленбека является стационарным гауссовским процессом.

Броуновский мост (как и процесс Орнштейна-Уленбека) является примером гауссовского процесса, приращения которого не являются независимыми .

Дробное броуновское движение — это гауссов процесс, ковариационная функция которого является обобщением функции винеровского процесса.

Закон нуля и единицы Дрисколла

Закон нуля и единицы Дрисколла - это результат, характеризующий выборочные функции, генерируемые гауссовским процессом.

Позволять $f$ быть гауссовским процессом со средним нулем $\left\{X_{t};t\in T\right\}$ с неотрицательно определенной ковариационной функцией $K$. Позволять ${\mathcal {H}}(R)$ быть гильбертовым пространством с воспроизводящим ядром с положительно определенным ядром. $R$.

Затем $$\lim _{n\to \infty }\operatorname {tr} [K_{n}R_{n}^{-1}]<\infty ,$$где $K_{n}$ и $R_{n}$ являются ковариационными матрицами всех возможных пар $n$ точки, подразумевает $$\Pr[f\in {\mathcal {H}}(R)]=1.$$

Более того, $$\lim _{n\to \infty }\operatorname {tr} [K_{n}R_{n}^{-1}]=\infty$$подразумевает $$\Pr[f\in {\mathcal {H}}(R)]=0.$$

Это имеет важные последствия, когда $K=R$, как $$\lim _{n\to \infty }\operatorname {tr} [R_{n}R_{n}^{-1}]=\lim _{n\to \infty }\operatorname {tr} [I]=\lim _{n\to \infty }n=\infty .$$

Таким образом, почти все выборочные пути гауссовского процесса со средним нулем и положительно определенным ядром $K$ будет лежать вне гильбертова пространства ${\mathcal {H}}(K)$.

Гауссовы процессы с линейными ограничениями

Для многих представляющих интерес приложений уже имеются некоторые ранее существовавшие знания о рассматриваемой системе. Рассмотрим, например, случай, когда результат гауссовского процесса соответствует магнитному полю; здесь реальное магнитное поле ограничено уравнениями Максвелла, и был бы желателен способ включить это ограничение в формализм гауссовского процесса, поскольку это, вероятно, улучшит точность алгоритма.

Метод включения линейных ограничений в гауссовские процессы уже существует:

Рассмотрим (векторную) выходную функцию $f(x)$ который, как известно, подчиняется линейному ограничению (т.е. ${\mathcal {F}}_{X}$ является линейным оператором) $${\mathcal {F}}_{X}(f(x))=0.$$Тогда ограничение ${\mathcal {F}}_{X}$ можно выполнить, выбрав $f(x)={\mathcal {G}}_{X}(g(x))$, где $g(x)\sim {\mathcal {GP}}(\mu _{g},K_{g})$ моделируется как гауссовский процесс, и нахождение ${\mathcal {G}}_{X}$ такой, что $${\mathcal {F}}_{X}({\mathcal {G}}_{X}(g))=0\qquad \forall g.$$Данный ${\mathcal {G}}_{X}$ и используя тот факт, что гауссовы процессы замкнуты относительно линейных преобразований, гауссов процесс для $f$ подчинение принуждению ${\mathcal {F}}_{X}$ становится $$f(x)={\mathcal {G}}_{X}g\sim {\mathcal {GP}}({\mathcal {G}}_{X}\mu _{g},{\mathcal {G}}_{X}K_{g}{\mathcal {G}}_{X'}^{\mathsf {T}}).$$Следовательно, линейные ограничения могут быть закодированы в среднее значение и ковариационную функцию гауссовского процесса.

Приложения

Пример регрессии гауссовского процесса (прогноз) в сравнении с другими моделями регрессии.

Гауссов процесс можно использовать в качестве априорного распределения вероятностей по функциям в байесовском выводе . Учитывая любой набор из N точек в желаемой области ваших функций, возьмите многомерный гауссиан , параметром ковариационной матрицы которого является матрица Грамма ваших N точек с некоторым желаемым ядром , и выполните выборку из этого гауссиана. Для решения задачи прогнозирования с несколькими выходами была разработана регрессия гауссовского процесса для векторной функции. В этом методе строится «большая» ковариация, описывающая корреляции между всеми входными и выходными переменными, взятыми в N точках в желаемой области. Этот подход был подробно разработан для матричных гауссовских процессов и обобщен на процессы с «более тяжелыми хвостами», такие как процессы Стьюдента .

Вывод непрерывных значений с помощью предшествующего гауссовского процесса известен как регрессия гауссовского процесса или кригинг ; расширение регрессии гауссовского процесса на несколько целевых переменных известно как кокригинг . Таким образом, гауссовские процессы полезны как мощный инструмент нелинейной многомерной интерполяции .

Гауссовы процессы также широко используются для решения задач численного анализа, таких как численное интегрирование, решение дифференциальных уравнений или оптимизация в области вероятностных чисел .

Гауссовские процессы также можно использовать, например, в контексте смешанных экспертных моделей. Основное обоснование такой структуры обучения состоит в предположении, что данное отображение не может быть хорошо отражено с помощью одной модели гауссовского процесса. Вместо этого пространство наблюдения разделено на подмножества, каждое из которых характеризуется своей функцией отображения; каждый из них изучается через различные компоненты гауссовского процесса в постулируемой смеси.

В естественных науках гауссовские процессы нашли применение в качестве вероятностных моделей астрономических временных рядов и в качестве предсказателей молекулярных свойств.

Предсказание гауссовского процесса, или кригинг

Дополнительная информация: Кригинг.

Гауссова регрессия процесса (прогноз) с квадратичным экспоненциальным ядром. Левый график основан на предыдущем распределении функции. Средние вытянуты сзади. Справа — средний прогноз с заштрихованным одним стандартным отклонением.

Когда речь идет об общей задаче регрессии гауссовского процесса (кригинг), предполагается, что для гауссовского процесса $f$ наблюдался в координатах $x$, вектор значений ⁠ $f(x)$⁠ — это всего лишь один образец из многомерного гауссовского распределения размерности, равной количеству наблюдаемых координат ⁠ $n$⁠ . Следовательно, в предположении распределения с нулевым средним ⁠ $f(x')\sim N(0,K(\theta ,x,x'))$⁠ , где ⁠ $K(\theta ,x,x')$⁠ — ковариационная матрица между всеми возможными парами ⁠ $(x,x')$⁠ для заданного набора гиперпараметров θ . Таким образом, логарифмическая предельная вероятность равна:

$$\log p(f(x')\mid \theta ,x)=-{\frac {1}{2}}\left(f(x)^{\mathsf {T}}K(\theta ,x,x')^{-1}f(x')+\log \det(K(\theta ,x,x'))+n\log 2\pi \right)$$

и максимизация этой предельной вероятности в направлении θ обеспечивает полную спецификацию гауссова процесса f . Здесь можно кратко отметить, что первый член соответствует штрафному члену за неспособность модели соответствовать наблюдаемым значениям, а второй член - штрафному члену, который увеличивается пропорционально сложности модели. Указав θ , делаем прогнозы относительно ненаблюдаемых значений ⁠ $f(x^{*})$⁠ в координатах x * тогда остается только вопрос отбора выборок из прогнозируемого распределения $p(y^{*}\mid x^{*},f(x),x)=N(y^{*}\mid A,B)$ где апостериорная средняя оценка A определяется как $$A=K(\theta ,x^{*},x)K(\theta ,x,x')^{-1}f(x)$$а апостериорная оценка дисперсии B определяется как: $$B=K(\theta ,x^{*},x^{*})-K(\theta ,x^{*},x)K(\theta ,x,x')^{-1}K(\theta ,x^{*},x)^{\mathsf {T}}$$где ⁠ $K(\theta ,x^{*},x)$⁠ — это ковариация между новой координатой оценки x * и всеми другими наблюдаемыми координатами x для данного вектора гиперпараметров θ , ⁠ $K(\theta ,x,x')$⁠ и ⁠ $f(x)$⁠ определены, как и раньше, и ⁠ $K(\theta ,x^{*},x^{*})$⁠ — это дисперсия в точке x *, определяемая θ . Важно отметить, что практически апостериорная средняя оценка ⁠ $f(x^{*})$⁠ («точечная оценка») — это просто линейная комбинация наблюдений ⁠ $f(x)$⁠ ; аналогичным образом дисперсия ⁠ $f(x^{*})$⁠ фактически не зависит от наблюдений ⁠ $f(x)$⁠ . Известным узким местом в прогнозировании гауссовского процесса является то, что вычислительная сложность вывода и оценки правдоподобия кубична по числу точек | x |, и поэтому может стать невозможным для больших наборов данных. Работы по разреженным гауссовским процессам, которые обычно основаны на идее построения репрезентативного множества для данного процесса f , пытаются обойти эту проблему. Метод кригинга можно использовать на скрытом уровне нелинейной модели смешанных эффектов для прогнозирования пространственных функций: этот метод называется скрытым кригингом.

Часто ковариация имеет вид ${\textstyle K(\theta ,x,x')={\frac {1}{\sigma ^{2}}}{\tilde {K}}(\theta ,x,x')}$, где $\sigma ^{2}$ является параметром масштабирования. Примерами являются ковариационные функции класса Матерна. Если этот параметр масштабирования $\sigma ^{2}$ либо известна, либо неизвестна (т.е. должна быть маргинализирована), то апостериорная вероятность, $p(\theta \mid D)$, т.е. вероятность гиперпараметров $\theta$ задан набор пар данных $D$ наблюдений за $x$ и $f(x)$, допускает аналитическое выражение.

Байесовские нейронные сети как гауссовские процессы

Дополнительная информация: Гауссов процесс нейронной сети.

Байесовские нейронные сети — это особый тип байесовских сетей , который возникает в результате вероятностной обработки моделей глубокого обучения и искусственных нейронных сетей и назначения предварительного распределения их параметрам . Вычисления в искусственных нейронных сетях обычно организованы в последовательные слои искусственных нейронов . Количество нейронов в слое называется шириной слоя. По мере увеличения ширины слоя многие байесовские нейронные сети сводятся к гауссовскому процессу с композиционным ядром закрытой формы . Этот гауссов процесс называется гауссовским процессом нейронной сети (NNGP). Он позволяет более эффективно оценивать прогнозы байесовских нейронных сетей и предоставляет аналитический инструмент для понимания глубокого обучения моделей .

Вычислительные проблемы

См. Также: Приближения гауссовского процесса.

В практических приложениях модели гауссовских процессов часто оцениваются на сетке, приводящей к многомерным нормальным распределениям. Использование этих моделей для прогнозирования или оценки параметров с использованием максимального правдоподобия требует оценки многомерной гауссовской плотности, которая включает в себя вычисление определителя и обратной ковариационной матрицы. Обе эти операции имеют кубическую вычислительную сложность, что означает, что даже для сеток скромных размеров обе операции могут иметь непомерно высокие вычислительные затраты. Этот недостаток привел к развитию множества методов аппроксимации .

См. также

• Линейная статистика Байеса
• Байесовская интерпретация регуляризации
• Кригинг
• Гауссово свободное поле
• Процесс Гаусса – Маркова
• Градиентный кригинг (GEK)
• t-процесс Стьюдента

Внешние ссылки

Литература

• Веб-сайт гауссовских процессов, включая текст книги Расмуссена и Уильямса «Гауссовы процессы для машинного обучения».
• Эбден, Марк (2015). «Гауссовы процессы: краткое введение». arXiv : 1505.02965 [ math.ST ].
• Обзор гауссовских случайных полей и корреляционных функций
• Эффективное обучение с подкреплением с использованием гауссовских процессов

Программное обеспечение

Дополнительная информация: Сравнение программного обеспечения гауссовского процесса.

• GPML: комплексный набор инструментов Matlab для регрессии и классификации GP.
• STK: небольшой (Matlab/Octave) набор инструментов для моделирования кригинга и GP.
• Модуль Кригинга в среде UQLab (Matlab)
• CODES Toolbox: реализации кригинга, вариационного кригинга и моделей мультиточности (Matlab)
• Функция Matlab/Octave для стационарных гауссовских полей
• Yelp MOE — механизм оптимизации «черного ящика», использующий гауссово процесс обучения.
• ooDACE. Архивировано 9 августа 2020 г. на Wayback Machine — гибкий объектно-ориентированный набор инструментов Kriging Matlab.
• GPstuff — набор инструментов для гауссовских процессов для Matlab и Octave.
• GPy — структура гауссовских процессов на Python.
• GSTools — набор геостатистических инструментов, включая регрессию гауссовского процесса, написанный на Python.
• Интерактивная демонстрация регрессии гауссовского процесса
• Базовая библиотека гауссовских процессов, написанная на C++11.
• scikit-learn — библиотека машинного обучения для Python, которая включает регрессию и классификацию гауссовых процессов.
• [1] - Набор инструментов Кригинга (KriKit) разработан в Институте био- и геонаук 1 (IBG-1) Forschungszentrum Jülich (FZJ).

Видеоуроки

• Основы гауссовского процесса Дэвида Маккея
• Обучение с помощью гауссовских процессов, Карл Эдвард Расмуссен
• Байесовский вывод и гауссовские процессы Карла Эдварда Расмуссена