Градиентный кригинг

Градиентный кригинг ( GEK ) — это метод суррогатного моделирования, используемый в технике. Суррогатная модель (также известная как метамодель , поверхность отклика или эмулятор) представляет собой прогноз выходных данных дорогостоящего компьютерного кода. ^[1] Этот прогноз основан на небольшом количестве оценок дорогостоящего компьютерного кода.

Введение

Сопряженные решатели теперь становятся доступными в ряде решателей вычислительной гидродинамики (CFD), таких как Fluent , OpenFOAM , SU2 и US3D. Первоначально разработанные для оптимизации , сопряженные решатели теперь находят все более широкое применение при количественной оценке неопределенности .

Линейное ускорение

Сопряженный решатель позволяет вычислить градиент интересующей величины по отношению ко всем параметрам расчета за счет одного дополнительного решения. Это потенциально приводит к линейному ускорению: вычислительные затраты на построение точного суррогатного кода уменьшаются и, как следствие, к ускорению вычислений. $s$ масштабируется линейно с числом $d$ проектных параметров.

Причина такого линейного ускорения проста. Предположим, мы бежим $N$ примитивные решения и $N$ сопряженное решает, общая стоимость $2N$ . Это приводит к $N+dN$ данные; $N$ значения количества процентов и $d$ частные производные в каждом из $N$ градиенты. Теперь предположим, что каждая частная производная предоставляет нашему суррогату столько же информации, сколько одно основное решение. Тогда общая стоимость получения того же объема информации только из простых решений составит $N+dN$ . Ускорение – это соотношение этих затрат: ^[2]^[3]

s={\frac {N+dN}{2N}}={\frac {1}{2}}+{\frac {1}{2}}d.

Линейное ускорение было продемонстрировано для взаимодействия жидкости и конструкции. задачи ^[2] и для трансзвукового профиля . ^[3]

Шум

Одна из проблем с сопряженными градиентами в CFD заключается в том, что они могут быть особенно зашумленными . ^[4]^[5] При использовании байесовской модели GEK позволяет учитывать не только информацию о градиенте, но и неопределенность этой информации о градиенте. ^[6]

Подход

При использовании GEK необходимо выполнить следующие шаги:

Создайте план эксперимента (DoE): DoE или «план выборки» представляет собой список различных мест в пространстве дизайна. DoE указывает, какие комбинации параметров будут использоваться для выборки компьютерного моделирования. В случае с Kriging и GEK распространенным выбором является использование проекта Latin Hypercube Design (LHS) с критерием «максимина». LHS-дизайн доступен в кодах сценариев, таких как MATLAB или Python .
Сделайте наблюдения: для каждого образца в нашем DoE проводится компьютерное моделирование, чтобы получить интересующую величину (QoI).
Постройте суррогат: используются уравнения-предикторы GEK для построения суррогатного условия на основе полученных наблюдений.

После того как суррогат создан, его можно использовать по-разному, например, для количественной оценки неопределенности на основе суррогата (UQ) или оптимизации .

Уравнения-предикторы

В байесовской структуре мы используем теорему Байеса для прогнозирования среднего кригинга и ковариации, зависящей от наблюдений. При использовании GEK наблюдения обычно являются результатами ряда компьютерных симуляций. GEK можно интерпретировать как форму регрессии гауссовского процесса .

Кригинг

В духе, ^[7] нас интересует результат $X$ нашего компьютерного моделирования, для которого мы предполагаем нормальное априорное распределение вероятностей :

X\sim {\mathcal {N}}(\mu ,P),

с априорным средним значением $\mu$ и априорная ковариационная матрица $P$ . Наблюдения $y$ имеют нормальную вероятность :

Y\mid x\sim {\mathcal {N}}(Hx,R),

с $H$ матрица наблюдения и $R$ ковариационная матрица ошибок наблюдения, которая содержит неопределенности наблюдения . После применения теоремы Байеса мы получаем нормально распределенное апостериорное распределение вероятностей со средним кригинговым значением:

\operatorname {E} (X\mid y)=\mu +K(y-H\mu ),

и ковариация кригинга:

\operatorname {cov} (X\mid y)=(I-KH)P,

где у нас есть матрица усиления:

K=PH^{T}(R+HPH^{T})^{-1}.

В кригинге априорная ковариационная матрица $P$ генерируется из ковариационной функции. Одним из примеров ковариационной функции является ковариация Гаусса:

P_{ij}=\sigma ^{2}\exp \left(-\sum _{k}{\frac {|\xi _{jk}-\xi _{ik}|^{2}}{2\theta _{k}^{2}}}\right),

где мы суммируем по размерам $k$ и $\xi$ являются входными параметрами. Гиперпараметры $\mu$ , $\sigma$ и $\theta$ можно оценить с помощью оценки максимального правдоподобия (MLE). ^[6]^[8] ^[9]

Косвенно СУМАСШЕДШИЙ

Существует несколько способов реализации GEK. Первый метод, косвенный GEK, определяет небольшой, но конечный размер шага. $h$ и использует информацию о градиенте для добавления синтетических данных к наблюдениям $y$ , см. например. ^[8] Косвенный кригинг чувствителен к выбору размера шага. $h$ и не может включать неопределенности наблюдений .

Прямой GEK (через априорную ковариационную матрицу)

Прямой GEK — это форма совместного кригинга, при которой мы добавляем информацию о градиенте в качестве копеременных. Это можно сделать, изменив предыдущую ковариацию $P$ или изменив матрицу наблюдения $H$ ; оба подхода приводят к одному и тому же предиктору GEK. Когда мы строим прямой GEK через априорную ковариационную матрицу, мы добавляем частные производные к $y$ и измените предыдущую ковариационную матрицу $P$ так, что он также содержит производные (и вторые производные) ковариационной функции, см., например, ^[10]. ^[6]Основные преимущества прямого GEK перед косвенным GEK: 1) нам не нужно выбирать размер шага, 2) мы можем включить неопределенности наблюдения для градиентов в $R$ и 3) он менее восприимчив к плохой настройке матрицы усиления. $K$ . ^[6]^[8]

Прямой ГЭК (через матрицу наблюдения)

Другой способ получить тот же прямой предиктор GEK — добавить к наблюдениям частные производные. $y$ и включить операторы частных производных в матрицу наблюдения $H$ , см. например. ^[11]

Градиентный кригинг для задач большой размерности (косвенный метод)

Текущие методы кригинга с усилением градиента плохо масштабируются с количеством точек отбора проб из-за быстрого роста размера корреляционной матрицы, в которой новая информация добавляется для каждой точки отбора проб в каждом направлении расчетного пространства. Кроме того, они плохо масштабируются с количеством независимых переменных из-за увеличения количества гиперпараметров, которые необходимо оценить. новый подход суррогатной модели с улучшенным градиентом, который радикально сокращает количество гиперпараметров за счет использования метода частичных наименьших квадратов Для решения этой проблемы разработан , обеспечивающего точность. Кроме того, этот метод позволяет контролировать размер корреляционной матрицы путем добавления только соответствующих точек, определенных с помощью информации, предоставленной методом частичных наименьших квадратов. Более подробную информацию см. ^[12]Этот подход реализован в наборе инструментов суррогатного моделирования (SMT) на Python ( https://github.com/SMTorg/SMT ) и работает в Linux, macOS и Windows. SMT распространяется по лицензии New BSD.

Кригинг с усиленным градиентом (прямой метод)

Универсальная дополненная структура предложена в ^[9] добавлять к наблюдениям производные любого порядка. Этот метод можно рассматривать как обобщение Direct GEK, учитывающее производные более высокого порядка. Кроме того, согласно этой схеме, наблюдения и производные не обязательно должны измеряться в одном и том же месте.

Пример: Коэффициент лобового сопротивления трансзвукового профиля.

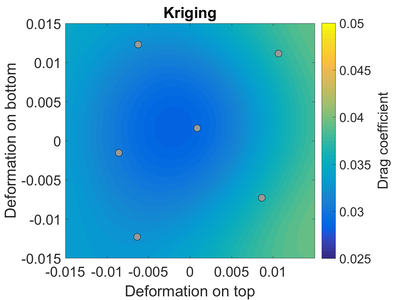
В качестве примера рассмотрим обтекание трансзвукового профиля . ^[3] Профиль работает при числе Маха 0,8 и угле атаки 1,25 градуса. Мы предполагаем, что форма профиля неопределенна; верхняя и нижняя части профиля могли сместиться вверх или вниз из-за производственных допусков. Другими словами, форма профиля, который мы используем, может немного отличаться от профиля, который мы разработали.

Справа мы видим эталонные результаты для коэффициента сопротивления аэродинамического профиля, основанные на большом количестве моделирования CFD. Обратите внимание, что наименьшее сопротивление, соответствующее «оптимальным» характеристикам, близко к недеформированной «базовой» конструкции профиля крыла (0,0).

После разработки плана отбора проб (обозначенного серыми точками) и запуска решателя CFD в этих местах отбора проб мы получаем суррогатную модель Кригинга. Суррогат Кригинга близок к эталону, но, возможно, не так близок, как хотелось бы.

На последнем рисунке мы улучшили точность этой суррогатной модели, включив информацию о сопряженном градиенте, указанную стрелками, и применив GEK.

Приложения

GEK нашел следующие применения:

1993: Проблема проектирования тестовой функции модели скважины. ^[13]
2002: Аэродинамический проект сверхзвукового бизнес-джета. ^[14]
2008: Количественная оценка неопределенности трансзвукового профиля с неопределенными параметрами формы. ^[10]
2009: Количественная оценка неопределенности для трансзвукового профиля с неопределенными параметрами формы. ^[8]
2012: Построение суррогатной модели для проблемы расхождения панелей и проблемы взаимодействия жидкости и конструкции . Демонстрация линейного ускорения. ^[2]
2013: Количественная оценка неопределенности для трансзвукового профиля с неопределенным углом атаки и числом Маха. ^[15]
2014: Количественная оценка неопределенности для RANS-моделирования профиля крыла с параметрами модели турбулентности k-эпсилон в качестве неопределенных входных данных. ^[6]
2015: Количественная оценка неопределенности для моделирования Эйлера трансзвукового профиля с неопределенными параметрами формы. Демонстрация линейного ускорения. ^[3]
2016: Построение суррогатной модели для двух задач взаимодействия жидкости и конструкции . ^[16]
2017: Большой обзор суррогатных моделей с градиентным усилением, включая множество подробностей, касающихся кригинга с градиентным усилением. ^[17]
2017: Распространение неопределенности в ядерной энергетической системе. ^[18]
2020: Оптимизация молекулярной геометрии. ^[19]

Ссылки

^ Митчелл, М.; Моррис, М. (1992). «Байесовский дизайн и анализ компьютерных экспериментов: два примера» (PDF) . Статистика Синица (2): 359–379.
^ Jump up to: ^а ^б ^с де Баар, JHS; Шольц, ТП; Верхузель, резюме; Дуайт, РП; ван Зейлен, АХ; Бейл, Х. (2012). «Эффективная количественная оценка неопределенности с помощью кригинга с усилением градиента: приложения в FSI» (PDF) . ECCOMAS, Вена, Австрия, 10–14 сентября .
^ Jump up to: ^а ^б ^с ^д де Баар, JHS; Шольц, ТП; Дуайт, РП (2015). «Использование сопряженных производных в многомерных метамоделях». Журнал АИАА . 53 (5): 1391–1395. Бибкод : 2015AIAAJ..53.1391D . дои : 10.2514/1.J053678 .
^ Дуайт, Р.; Брезиллон, Дж. (2006). «Влияние аппроксимации дискретного сопряжения на градиентную оптимизацию». Журнал АИАА . 44 (12): 3022–3031. Бибкод : 2006AIAAJ..44.3022D . CiteSeerX 10.1.1.711.4761 . дои : 10.2514/1.21744 .
^ Джайлз, М.; Дута, М.; Мюллер, Дж.; Пирс, Н. (2003). «Разработка алгоритмов для дискретных сопряженных методов» . Журнал АИАА . 41 (2): 198–205. Бибкод : 2003AIAAJ..41..198G . дои : 10.2514/02.1961 . S2CID 2106397 .
^ Jump up to: ^а ^б ^с ^д ^и де Баар, JHS; Дуайт, РП; Бейл, Х. (2014). «Усовершенствования кригинга с усилением градиента с использованием байесовской интерпретации» . Международный журнал количественной оценки неопределенности . 4 (3): 205–223. doi : 10.1615/Int.J.UncertaintyQuantification.2013006809 .
^ Викле, СК; Берлинер, LM (2007). «Байесовский учебник по ассимиляции данных». Физика Д. 230 (1–2): 1–16. Бибкод : 2007PhyD..230....1W . дои : 10.1016/j.physd.2006.09.017 .
^ Jump up to: ^а ^б ^с ^д Дуайт, РП; Хан, З.-Х. (2009). Эффективная количественная оценка неопределенности с использованием градиентного кригинга (PDF) . дои : 10.2514/6.2009-2276 . ISBN 978-1-60086-975-4 . S2CID 59019628 . {{cite book}}: |journal= игнорируется ( помогите )
^ Jump up to: ^а ^б Чжан, Шэн; Ян, Сю; Тиндел, Сэми; Линь, Гуан (2021). «Расширенное гауссово случайное поле: теория и вычисления». Дискретные и непрерывные динамические системы - С. 15 (4): 931. arXiv : 2009.01961 . дои : 10.3934/dcdss.2021098 . S2CID 221507566 .
^ Jump up to: ^а ^б Лоуренсо, Дж.; Сагаут, П. (2008). «Построение эффективных поверхностей отклика аэродинамических функций с помощью кригинга и кокригинга». Журнал АИАА . 46 (2): 498–507. Бибкод : 2008AIAAJ..46..498L . дои : 10.2514/1.32308 . S2CID 17895486 .
^ де Баар, JHS (2014). «Стохастические заменители измерений и компьютерные модели жидкостей» . Докторская диссертация, Делфтский технологический университет : 99–101.
^ Бухель, Массачусетс; Мартинс, JRRA (2018). «Градиентный кригинг для задач большой размерности». Инженерное дело с компьютерами . 35 : 157–173. arXiv : 1708.02663 . дои : 10.1007/s00366-018-0590-x . S2CID 3540630 .
^ Моррис, доктор медицины; Митчелл, Ти Джей; Юлвисакер, Д. (1993). «Байесовский дизайн и анализ компьютерных экспериментов: использование производных в прогнозировании поверхности» . Технометрика . 35 (3): 243–255. дои : 10.1080/00401706.1993.10485320 .
^ Чунг, Х.-С.; Алонсо, Джей-Джей (2002). «Использование градиентов для построения моделей аппроксимации кокригинга для многомерных задач оптимизации проектирования». 40-е собрание и выставка AIAA по аэрокосмическим наукам : 2002–03:17. CiteSeerX 10.1.1.12.4149 . дои : 10.2514/6.2002-317 .
^ Хан, З.-Х.; Горц, С.; Циммерманн, Р. (2013). «Улучшение суррогатного моделирования с переменной точностью с помощью кригинга с усилением градиента и обобщенной гибридной мостовой функции». Инженерное дело с компьютерами . 32 (1): 15–34. doi : 10.1016/j.ast.2012.01.006 .
^ Улаганатан, С.; Кокейт, И.; Дэн, Т.; Дегроот, Дж.; Лаерманс, Э. (2016). «Исследование эффективности кригинга с градиентным усилением» . Аэрокосмическая наука и технология . 25 (1): 177–189.
^ Лоран, Л.; Ле Риш, Р.; Сулье, Б.; Букар, П.-А. (2017). «Обзор метамоделей с улучшенным градиентом и приложений» (PDF) . Архив вычислительных методов в технике . 26 : 1–46. дои : 10.1007/s11831-017-9226-3 . S2CID 54625655 .
^ Локвуд, бакалавр; Анитеску, М. (2012). «Универсальный кригинг с градиентным усилением для распространения неопределенности» (PDF) . Ядерная наука и инженерия . 170 (2): 168–195. CiteSeerX 10.1.1.187.6097 . дои : 10.13182/NSE10-86 . S2CID 18465024 .
^ Рагги, Г.; Фдез. Гальван, И.; Риттерхофф, КЛ; Вашер, М.; Линд, Р. (2020). «Оптимизация молекулярной геометрии с ограниченной дисперсией на основе градиентного кригинга» . Журнал химической теории и вычислений . 16 (6): 3989–4001. дои : 10.1021/acs.jctc.0c00257 . ПМК 7304864 . ПМИД 32374164 .

[mitchell1992-1] Митчелл, М.; Моррис, М. (1992). «Байесовский дизайн и анализ компьютерных экспериментов: два примера» (PDF) . Статистика Синица (2): 359–379.

[debaar2012-2] Jump up to: ^а ^б ^с де Баар, JHS; Шольц, ТП; Верхузель, резюме; Дуайт, РП; ван Зейлен, АХ; Бейл, Х. (2012). «Эффективная количественная оценка неопределенности с помощью кригинга с усилением градиента: приложения в FSI» (PDF) . ECCOMAS, Вена, Австрия, 10–14 сентября .

[debaar2015-3] Jump up to: ^а ^б ^с ^д де Баар, JHS; Шольц, ТП; Дуайт, РП (2015). «Использование сопряженных производных в многомерных метамоделях». Журнал АИАА . 53 (5): 1391–1395. Бибкод : 2015AIAAJ..53.1391D . дои : 10.2514/1.J053678 .

[dwight2006-4] Дуайт, Р.; Брезиллон, Дж. (2006). «Влияние аппроксимации дискретного сопряжения на градиентную оптимизацию». Журнал АИАА . 44 (12): 3022–3031. Бибкод : 2006AIAAJ..44.3022D . CiteSeerX 10.1.1.711.4761 . дои : 10.2514/1.21744 .

[giles2003-5] Джайлз, М.; Дута, М.; Мюллер, Дж.; Пирс, Н. (2003). «Разработка алгоритмов для дискретных сопряженных методов» . Журнал АИАА . 41 (2): 198–205. Бибкод : 2003AIAAJ..41..198G . дои : 10.2514/02.1961 . S2CID 2106397 .

[debaar2014a-6] Jump up to: ^а ^б ^с ^д ^и де Баар, JHS; Дуайт, РП; Бейл, Х. (2014). «Усовершенствования кригинга с усилением градиента с использованием байесовской интерпретации» . Международный журнал количественной оценки неопределенности . 4 (3): 205–223. doi : 10.1615/Int.J.UncertaintyQuantification.2013006809 .

[7] Викле, СК; Берлинер, LM (2007). «Байесовский учебник по ассимиляции данных». Физика Д. 230 (1–2): 1–16. Бибкод : 2007PhyD..230....1W . дои : 10.1016/j.physd.2006.09.017 .

[dwight2009-8] Jump up to: ^а ^б ^с ^д Дуайт, РП; Хан, З.-Х. (2009). Эффективная количественная оценка неопределенности с использованием градиентного кригинга (PDF) . дои : 10.2514/6.2009-2276 . ISBN 978-1-60086-975-4 . S2CID 59019628 . {{cite book}}: |journal= игнорируется ( помогите )

[zhang2021-9] Jump up to: ^а ^б Чжан, Шэн; Ян, Сю; Тиндел, Сэми; Линь, Гуан (2021). «Расширенное гауссово случайное поле: теория и вычисления». Дискретные и непрерывные динамические системы - С. 15 (4): 931. arXiv : 2009.01961 . дои : 10.3934/dcdss.2021098 . S2CID 221507566 .

[laurenceau2008-10] Jump up to: ^а ^б Лоуренсо, Дж.; Сагаут, П. (2008). «Построение эффективных поверхностей отклика аэродинамических функций с помощью кригинга и кокригинга». Журнал АИАА . 46 (2): 498–507. Бибкод : 2008AIAAJ..46..498L . дои : 10.2514/1.32308 . S2CID 17895486 .

[11] де Баар, JHS (2014). «Стохастические заменители измерений и компьютерные модели жидкостей» . Докторская диссертация, Делфтский технологический университет : 99–101.

[bouhlel2018-12] Бухель, Массачусетс; Мартинс, JRRA (2018). «Градиентный кригинг для задач большой размерности». Инженерное дело с компьютерами . 35 : 157–173. arXiv : 1708.02663 . дои : 10.1007/s00366-018-0590-x . S2CID 3540630 .

[morris1993-13] Моррис, доктор медицины; Митчелл, Ти Джей; Юлвисакер, Д. (1993). «Байесовский дизайн и анализ компьютерных экспериментов: использование производных в прогнозировании поверхности» . Технометрика . 35 (3): 243–255. дои : 10.1080/00401706.1993.10485320 .

[chung2002-14] Чунг, Х.-С.; Алонсо, Джей-Джей (2002). «Использование градиентов для построения моделей аппроксимации кокригинга для многомерных задач оптимизации проектирования». 40-е собрание и выставка AIAA по аэрокосмическим наукам : 2002–03:17. CiteSeerX 10.1.1.12.4149 . дои : 10.2514/6.2002-317 .

[han2013-15] Хан, З.-Х.; Горц, С.; Циммерманн, Р. (2013). «Улучшение суррогатного моделирования с переменной точностью с помощью кригинга с усилением градиента и обобщенной гибридной мостовой функции». Инженерное дело с компьютерами . 32 (1): 15–34. doi : 10.1016/j.ast.2012.01.006 .

[ulaganathan2016-16] Улаганатан, С.; Кокейт, И.; Дэн, Т.; Дегроот, Дж.; Лаерманс, Э. (2016). «Исследование эффективности кригинга с градиентным усилением» . Аэрокосмическая наука и технология . 25 (1): 177–189.

[laurent2017-17] Лоран, Л.; Ле Риш, Р.; Сулье, Б.; Букар, П.-А. (2017). «Обзор метамоделей с улучшенным градиентом и приложений» (PDF) . Архив вычислительных методов в технике . 26 : 1–46. дои : 10.1007/s11831-017-9226-3 . S2CID 54625655 .

[lockwood2010-18] Локвуд, бакалавр; Анитеску, М. (2012). «Универсальный кригинг с градиентным усилением для распространения неопределенности» (PDF) . Ядерная наука и инженерия . 170 (2): 168–195. CiteSeerX 10.1.1.187.6097 . дои : 10.13182/NSE10-86 . S2CID 18465024 .

[Raggi2020-19] Рагги, Г.; Фдез. Гальван, И.; Риттерхофф, КЛ; Вашер, М.; Линд, Р. (2020). «Оптимизация молекулярной геометрии с ограниченной дисперсией на основе градиентного кригинга» . Журнал химической теории и вычислений . 16 (6): 3989–4001. дои : 10.1021/acs.jctc.0c00257 . ПМК 7304864 . ПМИД 32374164 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]