Современная сеть Хопфилда

Современные сети Хопфилда ^[1]^[2] (также известный как плотные ассоциативные воспоминания) . ^[3]) являются обобщением классических сетей Хопфилда , которые нарушают соотношение линейного масштабирования между количеством входных функций и количеством сохраненных воспоминаний. Это достигается за счет введения более сильных нелинейностей (либо в энергетическую функцию, либо в функции активации нейронов), приводящих к сверхлинейности. ^[3] (даже экспоненциальное ^[4]) емкость памяти как функция количества функциональных нейронов. Сеть по-прежнему требует достаточного количества скрытых нейронов. ^[5]

Ключевая теоретическая идея, лежащая в основе современных сетей Хопфилда, заключается в использовании энергетической функции и правила обновления, которые имеют более резкий пик вокруг сохраненных воспоминаний в пространстве конфигураций нейронов по сравнению с классической сетью Хопфилда. ^[3]

Классические сети Хопфилда

Сети Хопфилда ^[6]^[7] представляют собой рекуррентные нейронные сети с динамическими траекториями, сходящимися к состояниям аттрактора с фиксированной точкой и описываемыми энергетической функцией . Состояние каждого модельного нейрона ${\textstyle i}$ определяется зависящей от времени переменной $V_{i}$ , который может быть дискретным или непрерывным. Полная модель описывает математику того, как будущее состояние активности каждого нейрона зависит от известной нынешней или предыдущей активности всех нейронов.

В оригинальной модели ассоциативной памяти Хопфилда ^[6] переменные были двоичными, а динамика описывалась поочередным обновлением состояния нейронов. Энергетическая функция, квадратичная по $V_{i}$ была определена, а динамика заключалась в изменении активности каждого отдельного нейрона $i$ только в том случае, если это приведет к снижению общей энергии системы. Эта же идея была распространена на случай $V_{i}$ являющаяся непрерывной переменной, представляющей выходные данные нейрона $i$ , и $V_{i}$ является монотонной функцией входного тока. Динамика стала выражаться в виде системы дифференциальных уравнений первого порядка , для которых «энергия» системы всегда уменьшалась. ^[7] Энергия в непрерывном случае имеет один член, квадратичный по $V_{i}$ нейрона (как в бинарной модели) и второй член, который зависит от функции усиления ( функция активации ). Обладая многими желательными свойствами ассоциативной памяти, обе эти классические системы страдают от небольшого объема памяти, который линейно масштабируется с количеством входных функций. ^[6]

Дискретные переменные

Простой пример ^[3] сети Modern Hopfield можно записать в терминах двоичных переменных $V_{i}$ которые представляют собой активную $V_{i}=+1$ и неактивен $V_{i}=-1$ состояние модельного нейрона $i$ . $E=-\sum \limits _{\mu =1}^{N_{\text{mem}}}F{\Big (}\sum \limits _{i=1}^{N_{f}}\xi _{\mu i}V_{i}{\Big )}$ В этой формуле веса ${\textstyle \xi _{\mu i}}$ представляют собой матрицу векторов памяти (индекс $\mu =1...N_{\text{mem}}$ перечисляет различные воспоминания и индексирует $i=1...N_{f}$ перечисляет содержимое каждой памяти, соответствующей $i$ -й признак нейрона), а функция $F(x)$ является быстро растущей нелинейной функцией. Правило обновления для отдельных нейронов (в асинхронном случае) можно записать в следующем виде $V_{i}^{(t+1)}=\operatorname {sign} {\bigg [}\sum \limits _{\mu =1}^{N_{\text{mem}}}{\bigg (}F{\Big (}\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}-F{\Big (}-\xi _{\mu i}+\sum \limits _{j\neq i}\xi _{\mu j}V_{j}^{(t)}{\Big )}{\bigg )}{\bigg ]}$ в котором говорится, что для расчета обновленного состояния ${\textstyle i}$ -й нейрон сети сравнивает две энергии: энергию сети с энергией $i$ -й нейрон в состоянии ON и энергия сети с $i$ -й нейрон в состоянии ВЫКЛ, учитывая состояния оставшегося нейрона. Обновленное состояние $i$ -й нейрон выбирает состояние, которое имеет наименьшую из двух энергий. ^[3]

В предельном случае, когда нелинейная энергетическая функция квадратична $F(x)=x^{2}$ эти уравнения сводятся к знакомой функции энергии и правилу обновления классической бинарной сети Хопфилда. ^[6]

Емкость памяти этих сетей можно рассчитать для случайных двоичных шаблонов. Для функции мощности энергии $F(x)=x^{n}$ максимальное количество воспоминаний, которые можно сохранить и извлечь из этой сети без ошибок, определяется выражением ^[3] $N_{\text{mem}}^{\max }\approx {\frac {1}{2(2n-3)!!}}{\frac {N_{f}^{n-1}}{\ln(N_{f})}}$ Для показательной функции энергии ${\textstyle F(x)=e^{x}}$ емкость памяти экспоненциально зависит от количества функциональных нейронов ^[4] $N_{\text{mem}}^{\max }\approx 2^{N_{f}/2}$

Непрерывные переменные

Современные сети Хопфилда или плотные ассоциативные воспоминания лучше всего можно понять в непрерывных переменных и непрерывном времени. ^[1]^[5] Рассмотрим архитектуру сети, показанную на рис.1, и уравнения эволюции состояний нейронов. ^[5]

{\begin{cases}\tau _{f}{\frac {dx_{i}}{dt}}=\sum \limits _{\mu =1}^{N_{h}}\xi _{i\mu }f_{\mu }-x_{i}+I_{i}\\\tau _{h}{\frac {dh_{\mu }}{dt}}=\sum \limits _{i=1}^{N_{f}}\xi _{\mu i}g_{i}-h_{\mu }\end{cases}}

( 1 )

где токи характеристических нейронов обозначены ${\textstyle x_{i}}$ , а токи нейронов памяти обозначаются $h_{\mu }$ ( $h$ означает скрытые нейроны). Между функциональными нейронами и нейронами памяти нет синаптических связей. Матрица $\xi _{\mu i}$ обозначает силу синапсов функционального нейрона $i$ к нейрону памяти $\mu$ . Предполагается, что синапсы симметричны, так что одно и то же значение характеризует физический синапс, отличный от нейрона памяти. $\mu$ к функциональному нейрону $i$ . Выходы нейронов памяти и нейронов признаков обозначаются $f_{\mu }$ и $g_{i}$ , которые являются нелинейными функциями соответствующих токов. В общем, эти выходные данные могут зависеть от токов всех нейронов в этом слое, так что $f_{\mu }=f(\{h_{\mu }\})$ и ${\textstyle g_{i}=g(\{x_{i}\})}$ . Эти функции активации удобно определить как производные функций Лагранжа для двух групп нейронов.

f_{\mu }={\frac {\partial L_{h}}{\partial h_{\mu }}},\ \ \ \ {\text{and}}\ \ \ \ g_{i}={\frac {\partial L_{v}}{\partial x_{i}}}

( 2 )

Таким образом, конкретный вид уравнений состояний нейрона полностью определяется после задания функций Лагранжа. Наконец, постоянные времени для двух групп нейронов обозначаются через $\tau _{f}$ и $\tau _{h}$ , $I_{i}$ — это входной ток в сети, который можно регулировать с помощью представленных данных.

Общие системы нелинейных дифференциальных уравнений могут иметь много сложного поведения, которое может зависеть от выбора нелинейностей и начальных условий. Однако для сетей Хопфилда это не так: динамические траектории всегда сходятся к состоянию аттрактора с фиксированной точкой. Это свойство достигается потому, что эти уравнения специально разработаны так, что в их основе лежит энергетическая функция. ^[5]

E(t)={\Big [}\sum \limits _{i=1}^{N_{f}}(x_{i}-I_{i})g_{i}-L_{x}{\Big ]}+{\Big [}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }f_{\mu }-L_{h}{\Big ]}-\sum \limits _{\mu ,i}f_{\mu }\xi _{\mu i}g_{i}

( 3 )

Члены, сгруппированные в квадратные скобки, представляют собой преобразование Лежандра функции Лагранжа относительно состояний нейронов. Если матрицы Гессе функций Лагранжа положительно полуопределенны, то энергетическая функция гарантированно убывает на динамической траектории ^[5]

{\frac {dE(t)}{dt}}=-\tau _{f}\sum \limits _{i,j=1}^{N_{f}}{\frac {dx_{i}}{dt}}{\frac {\partial ^{2}L_{x}}{\partial x_{i}\partial x_{j}}}{\frac {dx_{j}}{dt}}-\tau _{h}\sum \limits _{\mu ,\nu =1}^{N_{h}}{\frac {dh_{\mu }}{dt}}{\frac {\partial ^{2}L_{h}}{\partial h_{\mu }\partial h_{\nu }}}{\frac {dh_{\nu }}{dt}}\leq 0

( 4 )

Это свойство позволяет доказать, что система динамических уравнений, описывающая временную эволюцию активности нейронов, в конечном итоге достигнет состояния аттрактора с фиксированной точкой.

В определенных ситуациях можно предположить, что динамика скрытых нейронов уравновешивается гораздо быстрее по сравнению с динамикой характерных нейронов. ${\textstyle \tau _{h}\ll \tau _{f}}$ . В этом случае стационарное решение второго уравнения системы ( 1 ) можно использовать для выражения токов скрытых единиц через выходы признакных нейронов. Это позволяет свести общую теорию ( 1 ) к эффективной теории только для признаковых нейронов. Полученные в результате эффективные правила обновления и энергии для различных распространенных вариантов функций Лагранжа показаны на рис.2. В случае логарифмической экспоненциальной функции Лагранжа правило обновления (если оно применяется один раз) для состояний характерных нейронов является механизмом внимания. ^[1] обычно используется во многих современных системах искусственного интеллекта (см. ^[5] для вывода этого результата из формулировки непрерывного времени).

Связь с классической сетью Хопфилда с непрерывными переменными

Классическая формулировка непрерывных сетей Хопфилда. ^[6] можно понять ^[5] как частный предельный случай современных сетей Хопфилда с одним скрытым слоем. Обычно описываются непрерывные сети Хопфилда для нейронов с градуированной реакцией. ^[6] динамическими уравнениями

\tau _{f}{\frac {dx_{i}}{dt}}=\sum \limits _{j=1}^{N_{f}}T_{ij}V_{j}-x_{i}+I_{i}

( 5 )

и энергетическая функция

E=-{\frac {1}{2}}\sum \limits _{i,j=1}^{N_{f}}T_{ij}V_{i}V_{j}-\sum \limits _{i=1}^{N_{f}}V_{i}I_{i}+\sum \limits _{i=1}^{N_{f}}\int \limits ^{V_{i}}g^{-1}(z)\,dz

( 6 )

где ${\textstyle V_{i}=g(x_{i})}$ , и $g^{-1}(z)$ является обратной функцией активации $g(x)$ . Эта модель представляет собой особый предел класса моделей, который называется моделями А. ^[5] со следующим выбором функций Лагранжа

L_{v}=\sum \limits _{i=1}^{N_{f}}\int \limits ^{x_{i}}g(x)\,dx,\ \ \ \ \ {\text{and}}\ \ \ \ \ L_{h}={\frac {1}{2}}\sum \limits _{\mu =1}^{N_{h}}h_{\mu }^{2}

( 7 )

что согласно определению ( 2 ) приводит к функциям активации

V_{i}=g(x_{i}),\ \ \ \ \ {\text{and}}\ \ \ \ \ f_{\mu }=h_{\mu }

( 8 )

Если интегрировать скрытые нейроны, то система уравнений ( 1 ) сводится к уравнениям для признакных нейронов ( 5 ) с $T_{ij}=\sum \limits _{\mu =1}^{N_{h}}\xi _{\mu i}\xi _{\mu j}$ , а общее выражение для энергии ( 3 ) сводится к эффективной энергии

E=-{\frac {1}{2}}\sum \limits _{i,j=1}^{N_{f}}T_{ij}V_{i}V_{j}-\sum \limits _{i=1}^{N_{f}}V_{i}I_{i}+\sum \limits _{i=1}^{N_{f}}{\Big (}x_{i}V_{i}-\int \limits ^{x_{i}}g(x)\,dx{\Big )}

( 9 )

Хотя первые два члена в уравнении ( 6 ) такие же, как и в уравнении ( 9 ), третьи члены внешне выглядят иначе. В уравнении ( 9 ) это преобразование Лежандра лагранжиана для характерных нейронов, а в ( 6 ) третий член представляет собой интеграл обратной функции активации. Тем не менее, эти два выражения фактически эквивалентны, поскольку производные функции и ее преобразования Лежандра являются обратными функциями друг друга. Самый простой способ увидеть, что эти два термина явно равны, — это дифференцировать каждый из них по $x_{i}$ . Результаты этих дифференцирований для обоих выражений равны $x_{i}g(x_{i})'$ . Таким образом, два выражения равны с точностью до аддитивной константы. Это завершает доказательство ^[5] что классическая сеть Хопфилда с непрерывными состояниями ^[6] является частным предельным случаем современной сети Хопфилда ( 1 ) с энергией ( 3 ).

Общая формулировка современной сети Хопфилда

Биологические нейронные сети обладают большой степенью гетерогенности в отношении разных типов клеток. В этом разделе описывается математическая модель полностью связанной сети Modern Hopfield, предполагающая крайнюю степень неоднородности: каждый нейрон уникален. ^[8] В частности, энергетическая функция и соответствующие динамические уравнения описываются в предположении, что каждый нейрон имеет свою собственную функцию активации и кинетическую шкалу времени. Предполагается, что сеть полностью связна, так что каждый нейрон связан с каждым другим нейроном с помощью симметричной матрицы весов. $W_{IJ}$ , индексы $I$ и $J$ перечислить разные нейроны в сети, см. рис.3. Самый простой способ математически сформулировать эту проблему — определить архитектуру через функцию Лагранжа. $L(\{x_{I}\})$ это зависит от активности всех нейронов в сети. Функция активации для каждого нейрона определяется как частная производная лагранжиана по активности этого нейрона.

g_{I}={\frac {\partial L}{\partial x_{I}}}

( 10 )

С биологической точки зрения можно подумать о $g_{I}$ как аксональный выход нейрона $I$ . В простейшем случае, когда лагранжиан аддитивен для разных нейронов, это определение приводит к активации, которая является нелинейной функцией активности этого нейрона. Для неаддитивных лагранжианов эта функция активации может зависеть от активности группы нейронов. Например, он может содержать контрастную (softmax) или разделительную нормализацию. Динамические уравнения, описывающие временную эволюцию данного нейрона, имеют вид ^[8]

\tau _{I}{\frac {dx_{I}}{dt}}=\sum \limits _{J=1}^{N}W_{IJ}g_{J}-x_{I}

( 11 )

Это уравнение принадлежит к классу моделей, называемых в нейробиологии моделями скорости стрельбы. Каждый нейрон $I$ собирает выходы аксонов $g_{J}$ от всех нейронов, взвешивает их с помощью синаптических коэффициентов $W_{IJ}$ и производит свою собственную, зависящую от времени активность $x_{I}$ . Временная эволюция имеет постоянную времени $\tau _{I}$ , которые в общем случае могут быть разными для каждого нейрона. Эта сеть имеет глобальную энергетическую функцию. ^[8]

E=\sum \limits _{I=1}^{N}x_{I}g_{I}-L-{\frac {1}{2}}\sum \limits _{I,J=1}^{N}g_{I}W_{IJ}g_{J}

( 12 )

где первые два члена представляют собой преобразование Лежандра функции Лагранжа относительно токов нейронов $x_{I}$ . Производная по времени этой энергетической функции может быть вычислена на динамических траекториях, ведущих к (см. ^[8] подробности)

{\frac {dE}{dt}}=-\sum \limits _{I,K=1}^{N}{\frac {dx_{I}}{dt}}M_{IK}{\frac {dx_{K}}{dt}}\leq 0,\ \ \ \ {\text{where}}\ \ \ \ M_{IK}=\tau _{I}{\frac {\partial ^{2}L}{\partial x_{I}\partial x_{K}}}

( 13 )

Последний знак неравенства имеет место при условии, что матрица $M_{IK}$ (или его симметричная часть) положительно полуопределена. Если вдобавок к этому энергетическая функция ограничена снизу, то нелинейные динамические уравнения гарантированно сходятся к состоянию аттрактора с неподвижной точкой. Преимущество формулирования этой сети в терминах функций Лагранжа состоит в том, что она позволяет легко экспериментировать с различным выбором функций активации и различным архитектурным расположением нейронов. Для всех этих гибких вариантов условия сходимости определяются свойствами матрицы $M_{IJ}$ и существование нижней границы энергетической функции.

Иерархическая ассоциативная сеть памяти

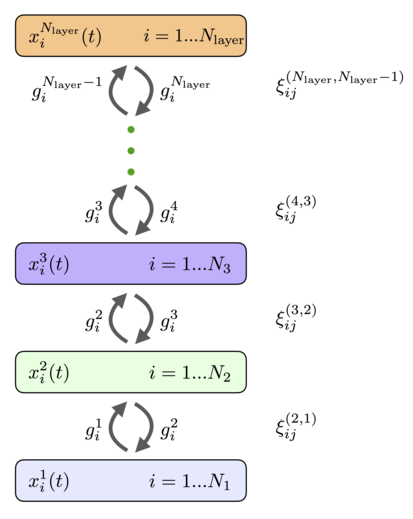
Нейроны могут быть организованы в слои так, чтобы каждый нейрон в данном слое имел одинаковую функцию активации и одинаковую динамическую шкалу времени. Если предположить, что между нейронами внутри слоя нет горизонтальных связей (латеральных связей) и нет связей с пропуском слоев, то общая полносвязная сеть ( 11 ), ( 12 ) сводится к архитектуре, показанной на рис.4. Он имеет $N_{\text{layer}}$ слои рекуррентно связанных нейронов с состояниями, описываемыми непрерывными переменными $x_{i}^{A}$ и функции активации $g_{i}^{A}$ , индекс $A$ перечисляет слои сети и индексирует $i$ перечисляет отдельные нейроны в этом слое. Функции активации могут зависеть от активности всех нейронов слоя. Каждый слой может иметь разное количество нейронов. $N_{A}$ . Эти нейроны рекуррентно связаны с нейронами предыдущего и последующих слоев. Матрицы весов, соединяющие нейроны в слоях $A$ и $B$ обозначаются $\xi _{ij}^{(A,B)}$ (порядок верхних индексов весов такой же, как и порядок нижних индексов, в примере выше это означает, что индекс $i$ перечисляет нейроны в слое $A$ и индекс $j$ перечисляет нейроны в слое $B$ ). Веса прямой связи и веса обратной связи равны. Динамические уравнения состояний нейронов можно записать в виде ^[8]

\tau _{A}{\frac {dx_{i}^{A}}{dt}}=\sum \limits _{j=1}^{N_{A-1}}\xi _{ij}^{(A,A-1)}g_{j}^{A-1}+\sum \limits _{j=1}^{N_{A+1}}\xi _{ij}^{(A,A+1)}g_{j}^{A+1}-x_{i}^{A}

( 14 )

с граничными условиями

g_{i}^{0}=0,\ \ \ \ \ {\text{and}}\ \ \ \ \ g_{i}^{N_{\text{layer}}+1}=0

( 15 )

Основным отличием этих уравнений от обычных сетей прямого распространения является наличие второго члена, отвечающего за обратную связь с более высокими уровнями. Эти нисходящие сигналы помогают нейронам нижних слоев принять решение о своей реакции на предъявленные стимулы. Следуя общему рецепту, удобно ввести функцию Лагранжа $L^{A}(\{x_{i}^{A}\})$ для $A$ -й скрытый слой, который зависит от активности всех нейронов этого слоя. ^[8] Функции активации в этом слое можно определить как частные производные лагранжиана

g_{i}^{A}={\frac {\partial L^{A}}{\partial x_{i}^{A}}}

( 16 )

С этими определениями функция энергии (Ляпунова) определяется выражением ^[8]

E=\sum \limits _{A=1}^{N_{\text{layer}}}{\Big [}\sum \limits _{i=1}^{N_{A}}x_{i}^{A}g_{i}^{A}-L^{A}{\Big ]}-\sum \limits _{A=1}^{N_{\text{layer}}-1}\sum \limits _{i=1}^{N_{A+1}}\sum \limits _{j=1}^{N_{A}}g_{i}^{A+1}\xi _{ij}^{(A+1,A)}g_{j}^{A}

( 17 )

Если функции Лагранжа или, что то же самое, функции активации выбраны таким образом, что гессиан для каждого слоя является положительно полуопределенным, а общая энергия ограничена снизу, эта система гарантированно сходится к состоянию аттрактора с фиксированной точкой. Производная по времени этой энергетической функции определяется выражением ^[8]

{\frac {dE}{dt}}=-\sum \limits _{A=1}^{N_{\text{layer}}}\tau _{A}\sum \limits _{i,j=1}^{N_{A}}{\frac {dx_{j}^{A}}{dt}}{\frac {\partial ^{2}L^{A}}{\partial x_{j}^{A}\partial x_{i}^{A}}}{\frac {dx_{i}^{A}}{dt}}\leq 0

( 18 )

Таким образом, иерархическая слоистая сеть действительно является сетью-аттрактором с глобальной энергетической функцией. Эта сеть описывается иерархическим набором синаптических весов, которые можно изучить для каждой конкретной проблемы.

Ссылки

^ Jump up to: ^а ^б ^с ^д Рамзауэр, Хуберт; и др. (2021). «Hopfield Networks — это все, что вам нужно». Международная конференция по обучению представлений . arXiv : 2008.02217 .
^ «Hopfield Networks — это все, что вам нужно» . слои хмеля . 25 августа 2020 г. Архивировано из оригинала 26 марта 2023 года . Проверено 4 мая 2023 г.
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г Кротов Дмитрий; Хопфилд, Джон (2016). «Плотная ассоциативная память для распознавания образов». Нейронные системы обработки информации . 29 : 1172–1180. arXiv : 1606.01164 .
^ Jump up to: ^а ^б ^с Демирджигил, Мете; и др. (2017). «О модели ассоциативной памяти с огромной емкостью» . Журнал статистической физики . 168 (2): 288–299. arXiv : 1702.01929 . Бибкод : 2017JSP...168..288D . дои : 10.1007/s10955-017-1806-y . S2CID 119317128 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Кротов Дмитрий; Хопфилд, Джон (2021). «Большая ассоциативная проблема памяти в нейробиологии и машинном обучении». Международная конференция по обучению представлений . arXiv : 2008.06996 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г Хопфилд, Джон (1982). «Нейронные сети и физические системы с возникающими коллективными вычислительными способностями» . Труды Национальной академии наук . 79 (8): 2554–2558. Бибкод : 1982PNAS...79.2554H . дои : 10.1073/pnas.79.8.2554 . ПМЦ 346238 . ПМИД 6953413 .
^ Jump up to: ^а ^б Хопфилд, Джон (1984). «Нейроны с дифференцированной реакцией обладают коллективными вычислительными свойствами, подобными свойствам нейронов с двумя состояниями» . Труды Национальной академии наук . 81 (10): 3088–3092. Бибкод : 1984PNAS...81.3088H . дои : 10.1073/pnas.81.10.3088 . ПМК 345226 . ПМИД 6587342 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Кротов, Дмитрий (2021). «Иерархическая ассоциативная память». arXiv : 2107.06446 [ cs.NE ].

[:3-1] Jump up to: ^а ^б ^с ^д Рамзауэр, Хуберт; и др. (2021). «Hopfield Networks — это все, что вам нужно». Международная конференция по обучению представлений . arXiv : 2008.02217 .

[2] «Hopfield Networks — это все, что вам нужно» . слои хмеля . 25 августа 2020 г. Архивировано из оригинала 26 марта 2023 года . Проверено 4 мая 2023 г.

[:1-3] Jump up to: ^а ^б ^с ^д ^и ^ж ^г Кротов Дмитрий; Хопфилд, Джон (2016). «Плотная ассоциативная память для распознавания образов». Нейронные системы обработки информации . 29 : 1172–1180. arXiv : 1606.01164 .

[:2-4] Jump up to: ^а ^б ^с Демирджигил, Мете; и др. (2017). «О модели ассоциативной памяти с огромной емкостью» . Журнал статистической физики . 168 (2): 288–299. arXiv : 1702.01929 . Бибкод : 2017JSP...168..288D . дои : 10.1007/s10955-017-1806-y . S2CID 119317128 .

[:4-5] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Кротов Дмитрий; Хопфилд, Джон (2021). «Большая ассоциативная проблема памяти в нейробиологии и машинном обучении». Международная конференция по обучению представлений . arXiv : 2008.06996 .

[:0-6] Jump up to: ^а ^б ^с ^д ^и ^ж ^г Хопфилд, Джон (1982). «Нейронные сети и физические системы с возникающими коллективными вычислительными способностями» . Труды Национальной академии наук . 79 (8): 2554–2558. Бибкод : 1982PNAS...79.2554H . дои : 10.1073/pnas.79.8.2554 . ПМЦ 346238 . ПМИД 6953413 .

[:6-7] Jump up to: ^а ^б Хопфилд, Джон (1984). «Нейроны с дифференцированной реакцией обладают коллективными вычислительными свойствами, подобными свойствам нейронов с двумя состояниями» . Труды Национальной академии наук . 81 (10): 3088–3092. Бибкод : 1984PNAS...81.3088H . дои : 10.1073/pnas.81.10.3088 . ПМК 345226 . ПМИД 6587342 .

[:5-8] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Кротов, Дмитрий (2021). «Иерархическая ассоциативная память». arXiv : 2107.06446 [ cs.NE ].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]