Спиновое стекло

Схематическое изображение случайной спиновой структуры спинового стекла (вверху) и упорядоченной структуры ферромагнетика ( внизу).

Стекло (аморфный SiO ₂ )

Кварц (кристаллический SiO ₂ )

Магнитный беспорядок спинового стекла по сравнению с ферромагнетиком аналогичен разупорядочению положения стекла (слева) по сравнению с кварцем (справа).

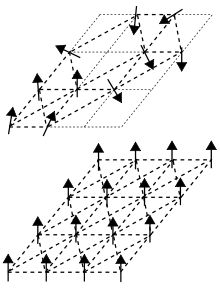
В физике конденсированного состояния спиновое стекло представляет собой магнитное состояние, характеризующееся случайностью, помимо кооперативного поведения при замораживании спинов при температуре, называемой «температурой замерзания» T _f . В ферромагнитных твердых телах магнитные спины атомов компонентов ориентированы в одном направлении. Спиновое стекло в отличие от ферромагнетика определяется как « неупорядоченное » магнитное состояние, в котором спины ориентированы случайным образом или без регулярного рисунка, а связи также случайны.

Термин «стекло» происходит от аналогии между магнитным беспорядком в спиновом стекле и позиционным беспорядком обычного химического стекла , например оконного стекла. В оконном стекле или любом аморфном твердом теле структура атомных связей крайне нерегулярна; напротив, кристалл имеет однородный рисунок атомных связей. В ферромагнитных твердых телах все магнитные спины ориентированы в одном направлении; кристалла это аналогично решетчатой ​​структуре .

Отдельные атомные связи в спиновом стекле представляют собой смесь примерно равного количества ферромагнитных связей (где соседи имеют одинаковую ориентацию) и антиферромагнитных связей (где соседи имеют совершенно противоположную ориентацию: северный и южный полюса перевернуты на 180 градусов). Эти узоры совмещенных и смещенных атомных магнитов создают так называемые фрустрированные взаимодействия — искажения геометрии атомных связей по сравнению с тем, что можно было бы наблюдать в обычном, полностью выровненном твердом теле. Они также могут создавать ситуации, когда более чем одно геометрическое расположение атомов стабильно.

Есть два основных аспекта спинового стекла. С физической стороны спиновые стекла — это реальные материалы с отличительными свойствами, обзор которых есть. С математической стороны широко изучаются и применяются простые модели статистической механики, основанные на реальных спиновых очках.

Спиновые стекла и сложные внутренние структуры, возникающие внутри них, называются « метастабильными », потому что они «застряли» в стабильных конфигурациях, отличных от конфигурации с самой низкой энергией (которая была бы ориентированной и ферромагнитной). Математическая сложность этих структур трудна, но плодотворна для изучения экспериментально или с помощью моделирования ; с приложениями к физике, химии, материаловедению и искусственным нейронным сетям в информатике .

Магнитное поведение

См. Также: Аморфный магнит.

Именно зависимость от времени отличает спиновые стекла от других магнитных систем.

спинового Выше температуры стеклования T _c , спиновое стекло демонстрирует типичное магнитное поведение (например, парамагнетизм ).

Если приложить магнитное поле при охлаждении образца до температуры перехода, намагниченность образца увеличивается, как описано законом Кюри . При достижении T _c образец становится спиновым стеклом, и дальнейшее охлаждение приводит к незначительному изменению намагниченности. Это называется намагниченностью , охлажденной полем .

Когда внешнее магнитное поле удаляется, намагниченность спинового стекла быстро падает до более низкого значения, известного как остаточная намагниченность.

Затем намагниченность медленно убывает по мере приближения к нулю (или некоторой небольшой доле первоначального значения – это остается неизвестным ). Этот затух не является экспоненциальным , и ни одна простая функция не может адекватно описать кривую зависимости намагниченности от времени. Этот медленный распад характерен для спиновых стекол. Экспериментальные измерения длительностью порядка нескольких дней показали постоянные изменения выше уровня шума приборов.

Спиновые стекла отличаются от ферромагнетиков тем, что после снятия внешнего магнитного поля с ферромагнитного вещества намагниченность неопределенно долго остается на остаточном значении. Парамагнетики отличаются от спиновых стекол тем, что после снятия внешнего магнитного поля намагниченность быстро падает до нуля без остаточной намагниченности. Распад быстрый и экспоненциальный.

Если образец охлаждается ниже T _c в отсутствие внешнего магнитного поля и прикладывается магнитное поле после перехода в фазу спинового стекла, происходит быстрый начальный рост до значения, называемого намагниченностью, охлажденной в нулевом поле . Затем происходит медленный дрейф вверх в сторону намагниченности, охлажденной полем.

Удивительно, но сумма двух сложных функций времени (охлажденной в нулевом поле и остаточной намагниченности) является константой, а именно, величиной, охлажденной полем, и, таким образом, обе имеют одинаковые функциональные формы со временем: по крайней мере, в пределе очень малых внешних полей.

Модель Эдвардса – Андерсона

Это похоже на модель Изинга . В этой модели мы имеем спины, расположенные на $d$-мерная решетка только с взаимодействиями ближайших соседей. Эту модель можно решить точно для критических температур, и наблюдается существование стеклообразной фазы при низких температурах. Гамильтониан для этой спиновой системы определяется выражением:

$H=-\sum _{\langle ij\rangle }J_{ij}S_{i}S_{j},$

где $S_{i}$ относится к матрице спина Паули для получастицы со спином в точке решетки $i$, и сумма более $\langle ij\rangle$ относится к суммированию по соседним точкам решетки $i$ и $j$. Отрицательное значение $J_{ij}$ обозначает взаимодействие антиферромагнитного типа между спинами в точках $i$ и $j$. Сумма пробегает все позиции ближайших соседей на решетке любой размерности. Переменные $J_{ij}$ представляющие магнитную природу спин-спиновых взаимодействий, называются переменными связи или связи.

Чтобы определить статистическую сумму этой системы, необходимо усреднить свободную энергию $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ где ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$, по всем возможным значениям $J_{ij}$. Распределение значений $J_{ij}$ принимается как гауссиан со средним $J_{0}$ и дисперсия $J^{2}$:

$P(J_{ij})={\sqrt {\frac {N}{2\pi J^{2}}}}\exp \left\{-{\frac {N}{2J^{2}}}\left(J_{ij}-{\frac {J_{0}}{N}}\right)^{2}\right\}.$

При определении свободной энергии методом реплик обнаруживается , что ниже определенной температуры существует новая магнитная фаза, называемая фазой спинового стекла (или стеклообразной фазой) системы, которая характеризуется исчезающей намагниченностью. $m=0$ наряду с ненулевым значением двухточечной корреляционной функции между спинами в одной и той же точке решетки, но в двух разных репликах:

$q=\sum _{i=1}^{N}S_{i}^{\alpha }S_{i}^{\beta }\neq 0,$

где $\alpha ,\beta$ являются индексами реплик. Таким образом, параметр порядка для фазового перехода из ферромагнетика в спиновое стекло равен $q$, и что для парамагнетика вращать стекло снова $q$. Следовательно, новый набор параметров порядка, описывающий три магнитные фазы, состоит как из $m$ и $q$.

В предположении симметрии реплик свободная энергия среднего поля определяется выражением:

${\begin{aligned}\beta f={}-{\frac {\beta ^{2}J^{2}}{4}}(1-q)^{2}+{\frac {\beta J_{0}m^{2}}{2}}-\int \exp \left(-{\frac {z^{2}}{2}}\right)\log \left(2\cosh \left(\beta Jz+\beta J_{0}m\right)\right)\,\mathrm {d} z.\end{aligned}}$

Модель Шеррингтона – Киркпатрика

Помимо необычных экспериментальных свойств, спиновые стекла являются предметом обширных теоретических и вычислительных исследований. Значительная часть ранних теоретических работ по спиновым стеклам была связана с формой теории среднего поля, основанной на наборе копий статистической суммы системы.

Важная, точно решаемая модель спинового стекла была представлена ​​Дэвидом Шеррингтоном и Скоттом Киркпатриком в 1975 году. Это модель Изинга с фрустрированными ферро- и антиферромагнитными связями на большом расстоянии. Оно соответствует приближению среднего поля спиновых стекол, описывающему медленную динамику намагниченности и сложное неэргодическое состояние равновесия.

В отличие от модели Эдвардса-Андерсона (ЭА), в системе, хотя и рассматриваются только двухспиновые взаимодействия, диапазон каждого взаимодействия может быть потенциально бесконечным (порядка размера решетки). Таким образом, мы видим, что любые два спина могут быть связаны ферромагнитной или антиферромагнитной связью, и их распределение задается точно так же, как и в случае модели Эдвардса–Андерсона. Гамильтониан для модели SK очень похож на модель EA:

$H=-{\frac {1}{\sqrt {N}}}\sum _{i<j}J_{ij}S_{i}S_{j}$

где $J_{ij},S_{i},S_{j}$ имеют те же значения, что и в модели советника. Равновесное решение модели после некоторых первоначальных попыток Шеррингтона, Киркпатрика и других было найдено Джорджио Паризи в 1979 году с помощью метода реплик. Последующие работы по интерпретации решения Паризи — М. Мезара , Г. Паризи , М. А. Вирасоро и многих других — выявили сложную природу стеклообразной низкотемпературной фазы, характеризующейся нарушением эргодичности, ультраметричностью и несамоусреднённостью. Дальнейшие разработки привели к созданию метода резонаторов , который позволил изучать низкотемпературную фазу без реплик. Строгое доказательство решения Паризи было предоставлено в работе Франческо Герра и Мишеля Талагранда .

Фазовая диаграмма

Кривая де Алмейды-Таулесса.

При наличии однородного внешнего магнитного поля величиной $M$, энергетическая функция становится $$H=-{\frac {1}{\sqrt {N}}}\sum _{i<j}J_{ij}S_{i}S_{j}-M\sum _{i}S_{i}$$Пусть все муфты $J_{ij}$ представляют собой выборки IID из гауссовского распределения среднего значения 0 и дисперсии $J^{2}$. В 1979 году JRL де Алмейда и Дэвид Таулесс. обнаружил, что, как и в случае с моделью Изинга, решение модели SK в среднем поле становится нестабильным в условиях низкой температуры и низкого магнитного поля.

Область устойчивости на фазовой диаграмме модели СК определяется двумя безразмерными параметрами $x:={\frac {kT}{J}},\quad y:={\frac {M}{J}}$. Его фазовая диаграмма состоит из двух частей, разделенных кривой де Алмейды-Таулесса . Кривая представляет собой решение множества уравнений $${\begin{aligned}&x^{2}={\frac {1}{(2\pi )^{1/2}}}\int \mathrm {d} z\;\mathrm {e} ^{-{\frac {1}{2}}z^{2}}\operatorname {sech} ^{4}\left({\frac {q^{1/2}z+y}{x}}\right),\\&q={\frac {1}{(2\pi )^{1/2}}}\int \mathrm {d} z\;\mathrm {e} ^{-{\frac {1}{2}}z^{2}}\tanh ^{2}\left({\frac {q^{1/2}z+y}{x}}\right).\end{aligned}}$$Фазовый переход происходит при $x=1$. Чуть ниже него у нас есть $$y^{2}\approx {\frac {4}{3}}(1-x)^{3}.$$При низкой температуре и высоком пределе магнитного поля линия $$x\approx {\frac {4}{3{\sqrt {2\pi }}}}e^{-{\frac {1}{2}}y^{2}}$$

Модель бесконечного радиуса действия

Это также называется «моделью p-спина». Модель бесконечного радиуса действия представляет собой обобщение модели Шеррингтона–Киркпатрика, в которой мы рассматриваем не только двухспиновые взаимодействия, но и $p$-спиновые взаимодействия, где $p\leq N$ и $N$ общее количество вращений. В отличие от модели Эдвардса-Андерсона, но аналогично модели СК, диапазон взаимодействия бесконечен. Гамильтониан для этой модели описывается следующим образом:

$H=-\sum _{i_{1}<i_{2}<\cdots <i_{p}}J_{i_{1}\dots i_{p}}S_{i_{1}}\cdots S_{i_{p}}$

где $J_{i_{1}\dots i_{p}},S_{i_{1}},\dots ,S_{i_{p}}$ имеют те же значения, что и в модели советника. $p\to \infty$ предел этой модели известен как модель случайной энергии . В этом пределе вероятность существования спинового стекла в определенном состоянии зависит только от энергии этого состояния, а не от отдельных спиновых конфигураций в нем.Для решения этой модели обычно предполагается гауссово распределение магнитных связей по решетке. Ожидается, что любое другое распределение даст тот же результат, как следствие центральной предельной теоремы . Функция распределения Гаусса со средним значением ${\frac {J_{0}}{N}}$ и дисперсия ${\frac {J^{2}}{N}}$, определяется как:

$P\left(J_{i_{1}\cdots i_{p}}\right)={\sqrt {\frac {N^{p-1}}{J^{2}\pi p!}}}\exp \left\{-{\frac {N^{p-1}}{J^{2}p!}}\left(J_{i_{1}\cdots i_{p}}-{\frac {J_{0}p!}{2N^{p-1}}}\right)\right\}$

Параметры порядка для этой системы определяются намагниченностью $m$ и двухточечная спиновая корреляция между спинами в одном и том же месте $q$, в двух разных репликах, которые такие же, как и для модели SK. Эту модель бесконечного диапазона можно явно решить для свободной энергии. с точки зрения $m$ и $q$, в предположении симметрии реплики, а также нарушения симметрии 1-реплики.

${\begin{aligned}\beta f={}&{\frac {1}{4}}\beta ^{2}J^{2}q^{p}-{\frac {1}{2}}p\beta ^{2}J^{2}q^{p}-{\frac {1}{4}}\beta ^{2}J^{2}+{\frac {1}{2}}\beta J_{0}pm^{p}+{\frac {1}{4{\sqrt {2\pi }}}}p\beta ^{2}J^{2}q^{p-1}+{}\\&\int \exp \left(-{\frac {1}{2}}z^{2}\right)\log \left(2\cosh \left(\beta Jz{\sqrt {{\frac {1}{2}}pq^{p-1}}}+{\frac {1}{2}}\beta J_{0}pm^{p-1}\right)\right)\,\mathrm {d} z\end{aligned}}$

Неэргодическое поведение и приложения

Термодинамическая система является эргодической , когда при наличии любого (равновесного) экземпляра системы она в конечном итоге посещает любое другое возможное (равновесное) состояние (с той же энергией). Одной из характеристик систем спинового стекла является то, что ниже температуры замерзания $T_{\text{f}}$экземпляры попадают в «неэргодический» набор состояний: система может колебаться между несколькими состояниями, но не может переходить в другие состояния с эквивалентной энергией. Интуитивно можно сказать, что система не может выйти из глубоких минимумов иерархически неупорядоченного энергетического ландшафта ; расстояния между минимумами задаются ультраметрикой с высокими энергетическими барьерами между минимумами. Коэффициент участия подсчитывает количество состояний, доступных из данного экземпляра, то есть количество состояний, участвующих в основном состоянии . Эргодический аспект спинового стекла сыграл важную роль в присуждении половины Нобелевской премии по физике 2021 года Джорджо Паризи .

Для физических систем, таких как разбавленный марганец в меди, температура замерзания обычно составляет всего 30 кельвинов (-240 ° C), и поэтому магнетизм спинового стекла практически не имеет применения в повседневной жизни. Однако неэргодические состояния и суровые энергетические ландшафты весьма полезны для понимания поведения некоторых нейронных сетей , включая сети Хопфилда , а также многих проблем информатики оптимизации и генетики .

Спиновое стекло без структурного беспорядка

Элементарный кристаллический неодим парамагнитен при комнатной температуре и становится антиферромагнетиком несоизмеримого порядка при охлаждении ниже 19,9 К. Ниже этой температуры перехода он демонстрирует сложный набор магнитных фаз. которые имеют большие времена спиновой релаксации и поведение спинового стекла, не зависящее от структурного беспорядка.

История

Подробный отчет об истории спиновых стекол с начала 1960-х до конца 1980-х годов можно найти в серии популярных статей Филипа Андерсона в журнале Physics Today .

Открытие

В 1930-х годах ученые-материалисты обнаружили эффект Кондо , при котором удельное сопротивление номинально чистого золота достигает минимума при 10 К, а также для номинально чистой меди при 2 К. Позже стало понятно, что эффект Кондо возникает, когда немагнитный металл пропитывается разбавленные магнитные атомы.

Необычное поведение наблюдалось в сплаве железо-золото (Au Fe ) и сплаве марганец-медь (Cu Mn ) при содержании от 1 до 10 атомных процентов . Каннелла и Мидош наблюдались в 1972 году. что Au Fe имел неожиданный пик восприимчивости, похожий на выступ , при четко определенной температуре, которую позже назвали температурой замерзания спинового стекла .

Его еще называли «миктомагнит» (микто-по-гречески «смешанный»). Этот термин возник из наблюдения, что эти материалы часто содержат смесь ферромагнетиков ( $J>0$) и антиферромагнитный ( $J<0$) взаимодействия, приводящие к их неупорядоченной магнитной структуре. Этот термин вышел из употребления по мере развития теоретического понимания спиновых стекол, признавшего, что магнитная фрустрация возникает не просто из-за простой смеси ферро- и антиферромагнитных взаимодействий, но из-за их хаотичности и фрустрации в системе.

Модель Шеррингтона-Киркпатрика

Шеррингтон и Киркпатрик предложили модель SK в 1975 году и решили ее методом реплик. Они обнаружили, что при низких температурах его энтропия становится отрицательной, что, по их мнению, произошло потому, что метод реплик является эвристическим методом, который не применяется при низких температурах.

Затем было обнаружено, что метод реплик был правильным, но проблема заключается в том, что низкотемпературное нарушение симметрии в модели SK не может быть охарактеризовано исключительно параметром порядка Эдвардса-Андерсона. Вместо этого необходимы дополнительные параметры порядка, что приводит к нарушению анзаца реплики Джорджио Паризи . При полном анзаце разрушения реплик требуется бесконечно много параметров порядка, чтобы охарактеризовать устойчивое решение.

Приложения

Формализм теории среднего поля реплик также применялся при изучении нейронных сетей , где он позволял рассчитывать такие свойства, как емкость памяти простых архитектур нейронных сетей, без необходимости алгоритма обучения (например, обратного распространения ошибки разработки или разработки ). реализовано.

Более реалистичные модели спинового стекла с короткодействующими фрустрированными взаимодействиями и беспорядком, такие как модель Гаусса, в которой связи между соседними спинами следуют гауссовскому распределению , также широко изучались, особенно с использованием моделирования Монте-Карло . Эти модели отображают фазы спинового стекла, окаймленные резкими фазовыми переходами .

Помимо своей значимости в физике конденсированного состояния, теория спинового стекла приобрела ярко выраженный междисциплинарный характер с приложениями к теории нейронных сетей , информатике, теоретической биологии, эконофизике и т. д.

Модели спинового стекла были адаптированы к складчатой ​​воронки модели белка .

См. также

• Аморфный магнит
• Антиферромагнитное взаимодействие
• Полостной метод
• Кристаллическая структура
• Геометрическое разочарование
• Ориентационное стекло
• Фазовый переход
• Подавленный беспорядок
• Модель случайной энергии
• Трюк с репликой
• Физика твердого тела
• Вращение льда

Литература

Выставки

• Штейн, Дэниел Л.; Ньюман, Чарльз М. (2013). Спиновые очки и сложность . Праймеры в сложных системах. Принстон: Издательство Принстонского университета. ISBN  978-0-691-14733-8 . Популярное изложение, с минимальным количеством математики.
• Монтанари, Андреа; Сен, Субхабрата (9 января 2024 г.). «Дружественное руководство по методам определения среднего поля спинового стекла для нефизиков» . Основы и тенденции в машинном обучении . 17 (1): 1–173. arXiv : 2204.02909 . дои : 10.1561/2200000105 . ISSN   1935-8237 . Введение в практическое руководство.
• Мезар, Марк; Монтанари, Андреа (2009). Информация, физика и вычисления . Оксфорд, Великобритания: Издательство Оксфордского университета. ISBN  9780198570837 . OCLC   234430714 . Первые 15 глав черновой версии 2008 г. доступны на сайте www.stat.ucla.edu. Учебник, посвященный методу полости и его приложениям в информатике, особенно проблемам удовлетворения ограничений .
• Нисимори, Хидетоши (2001). Статистическая физика спиновых стекол и обработка информации: введение . Международная серия монографий по физике. Оксфорд; Нью-Йорк: Издательство Оксфордского университета. ISBN  978-0-19-850940-0 . OCLC   47063323 . Введение было сосредоточено на приложениях информатики, включая нейронные сети.
• Мидош, ЖА (1993). Спиновые стекла: экспериментальное введение . Лондон; Вашингтон, округ Колумбия: Тейлор и Фрэнсис. ISBN  978-0-7484-0038-6 . Основное внимание уделяется экспериментально измеряемым свойствам спиновых стекол (таких как медно-марганцевый сплав).
• Фишер, К.Х.; Герц, Джон (1991). Спиновые очки . Кембриджские исследования по магнетизму. Кембридж; Нью-Йорк, штат Нью-Йорк, США: Издательство Кембриджского университета. ISBN  978-0-521-34296-4 . Охватывает среднюю теорию поля , экспериментальные данные и численное моделирование.
• Мезар, Марк; Паризи, Джорджо ; Вирасоро, Мигель Анхель (1987), Теория спинового стекла и не только , Сингапур: World Scientific, ISBN  978-9971-5-0115-0 . Ранняя экспозиция, содержащая достижения, существовавшие до 1990 года, такие как трюк с репликами .
• Де Доминисис, Сирано; Джардина, Ирен (2006). Случайные поля и спиновые стекла: подход теории поля . Кембридж, Великобритания ; Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-84783-4 . OCLC   70764844 . Подход через статистическую теорию поля .
• Талагранд, Мишель (2010). Модели среднего поля для спиновых стекол. 1: Основные примеры . Результаты математики и ее границы (переиздание в мягкой обложке из харковского издания, 1-е изд., 2010 г.). Берлин Гейдельберг: Springer. ISBN  978-3-642-26598-3 . и Талагранд, Мишель (2011). Модели среднего поля для спиновых стекол . Результаты математики и ее пограничные области. 3-я серия = Серия современных обзоров по математике. Гейдельберг; Нью-Йорк: Спрингер. ISBN  978-3-642-15201-6 . OCLC   733249730 . . Сборник строго доказуемых результатов.

Первоисточники

• Эдвардс, Сан-Франциско; Андерсон, П.В. (1975), «Теория спиновых стекол», Journal of Physics F: Metal Physics , 5 (5): 965–974, Бибкод : 1975JPhF....5..965E , doi : 10.1088/0305-4608 /05.05.017 . ЩитКвадратная Капча
• Шеррингтон, Дэвид; Киркпатрик, Скотт (1975), «Разрешимая модель спинового стекла», Physical Review Letters , 35 (26): 1792–1796, Бибкод : 1975PhRvL..35.1792S , doi : 10.1103/PhysRevLett.35.1792 . Резюме Papercore http://papercore.org/Sherrington1975
• Нордблад, П.; Лундгрен, Л.; Сандлунд, Л. (1986), «Связь между релаксацией охлаждения в нулевом поле и термоостаточной намагниченностью в спиновых стеклах», Journal of Magnetism and Magnetic Materials , 54 : 185–186, Bibcode : 1986JMMM...54.. 185Н , номер документа : 10.1016/0304-8853(86)90543-3 .
• Биндер, К .; Янг, AP (1986), «Спиновые очки: экспериментальные факты, теоретические концепции и открытые вопросы», Reviews of Modern Physics , 58 (4): 801–976, Бибкод : 1986RvMP...58..801B , doi : 10.1103 /RevModPhys.58.801 .
• Брингельсон, Джозеф Д.; Волинс, Питер Г. (1987), «Спиновые стекла и статистическая механика сворачивания белков», Proceedings of the National Academy of Sciences , 84 (21): 7524–7528, Bibcode : 1987PNAS...84.7524B , doi : 10.1073 /pnas.84.21.7524 , PMC   299331 , PMID   3478708 ....
• Паризи, Г. (1980), «Параметр порядка для спиновых стекол: функция в интервале 0–1» (PDF) , J. Phys. А: Математика. Gen. , 13 (3): 1101–1112, Bibcode : 1980JPhA...13.1101P , doi : 10.1088/0305-4470/13/3/042 Резюме Papercore http://papercore.org/Parisi1980 .
• Талагранд, Мишель (2000), «Нарушение симметрии реплик и экспоненциальные неравенства для модели Шеррингтона-Киркпатрика», Annals of Probability , 28 (3): 1018–1062, doi : 10.1214/aop/1019160325 , JSTOR   2652978 .
• Герра, Ф.; Тонинелли, Флорида (2002), «Термодинамический предел в моделях спинового стекла среднего поля», Communications in Mathematical Physics , 230 (1): 71–79, arXiv : cond-mat/0204280 , Bibcode : 2002CMaPh.230...71G , doi : 10.1007/s00220-002-0699-y , S2CID   16833848

Внешние ссылки

• Статистика частотности термина «Спиновое стекло» на arxiv.org