Потенциальная энергетическая поверхность
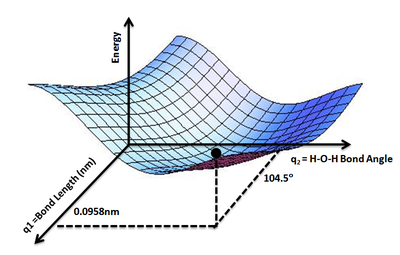

Поверхность потенциальной энергии ( ППЭ ) или энергетический ландшафт описывает энергию системы , особенно совокупности атомов, с точки зрения определенных параметров , обычно положений атомов. Поверхность функцию может определять энергию как одной или нескольких координат; если есть только одна координата, поверхность называется кривой потенциальной энергии или энергетическим профилем . Примером может служить потенциал Морзе/Дальнодействия .
Полезно использовать аналогию с ландшафтом: для системы с двумя степенями свободы (например, двумя длинами связей) значение энергии (аналогия: высота земли) является функцией двух длин связей (аналогия: координаты положения на местности). [1]
Концепция PES находит применение в таких областях, как физика , химия и биохимия , особенно в теоретических разделах этих предметов. Его можно использовать для теоретического исследования свойств структур, состоящих из атомов, например, для определения минимальной энергетической формы молекулы или расчета скорости реакции химической . Его можно использовать для описания всех возможных конформаций молекулярного объекта или пространственного положения взаимодействующих молекул в системе, или параметров и соответствующих им энергетических уровней, обычно свободной энергии Гиббса . Геометрически энергетический ландшафт представляет собой график энергетической функции в конфигурационном пространстве системы. Этот термин также используется в более общем смысле в геометрической перспективе математической оптимизации , когда областью определения функции потерь является пространство параметров некоторой системы.
Математическое определение и расчет
[ редактировать ]Геометрию набора атомов можно описать вектором r , элементы которого представляют позиции атомов. Вектор r может быть набором декартовых координат атомов или также набором межатомных расстояний и углов.
Учитывая r , энергия как функция позиций, E ( r ) , является значением E ( r ) для всех r , представляющих интерес. Используя аналогию с ландшафтом из введения, E обозначает высоту «энергетического ландшафта», так что возникает концепция потенциальной энергетической поверхности .
Чтобы изучить химическую реакцию с использованием PES в зависимости от положений атомов, необходимо рассчитать энергию для каждого интересующего атомного расположения. Методы расчета энергии определенного атомного расположения атомов хорошо описаны в статьях по вычислительной химии , и здесь основное внимание будет уделено поиску приближений E ( r ) для получения более детальной информации об энергетическом положении.
Для очень простых химических систем или когда делаются упрощающие приближения к межатомным взаимодействиям, иногда можно использовать аналитически полученное выражение для энергии как функции положения атомов. Примером может служить Лондона - Айринга - Полани -Сато. потенциал [2] [3] [4] для системы H + H 2 как функция трех расстояний HH.
Для более сложных систем расчет энергии определенного расположения атомов часто оказывается слишком дорогим с точки зрения вычислений, чтобы можно было получить крупномасштабное представление поверхности. Для этих систем возможный подход состоит в том, чтобы вычислить только сокращенный набор точек на PES, а затем использовать более дешевый в вычислительном отношении метод интерполяции, например интерполяцию Шепарда , чтобы заполнить пробелы. [5]
Приложение
[ редактировать ]PES — это концептуальный инструмент, помогающий анализировать молекулярную геометрию и динамику химических реакций . После оценки необходимых точек на PES точки можно классифицировать в соответствии с первой и второй производными энергии по положению, которые соответственно представляют собой градиент и кривизну . Стационарные точки (или точки с нулевым градиентом) имеют физический смысл: минимумы энергии соответствуют физически стабильным химическим соединениям, а седловые точки соответствуют переходным состояниям , точке с наивысшей энергией на координате реакции (которая представляет собой путь с наименьшей энергией, соединяющий химический реагент с химический продукт).
Этот термин полезен при изучении сворачивания белков ; Хотя теоретически белок может существовать в почти бесконечном количестве конформаций по своему энергетическому ландшафту, в действительности белки сворачиваются (или «расслабляются») во вторичные и третичные структуры , которые обладают минимально возможной свободной энергией . Ключевой концепцией энергетического ландшафтного подхода к сворачиванию белков является гипотеза складчатой воронки .
В катализе при разработке новых катализаторов или очистке существующих считается, что энергетические ландшафты позволяют избегать низкоэнергетических или высокоэнергетических промежуточных продуктов, которые могут остановить реакцию или потребовать чрезмерной энергии для достижения конечных продуктов. [6]
В моделях остекления локальные минимумы энергетического ландшафта соответствуют метастабильным низкотемпературным состояниям термодинамической системы . [7] [8]
В машинном обучении искусственные нейронные сети можно анализировать с использованием аналогичных подходов. [9] Например, нейронная сеть может идеально соответствовать обучающему набору , что соответствует глобальному минимуму нулевых потерь, но переобучать модель («изучение шума» или « запоминание обучающего набора»). Понимание того, когда это происходит, можно изучить, используя геометрию соответствующего энергетического ландшафта. [10]
Привлекательные и отталкивающие поверхности
[ редактировать ]Поверхности потенциальной энергии химических реакций можно классифицировать как притягивающие или отталкивающие путем сравнения длин связей в активированном комплексе по сравнению с длинами связей реагентов и продуктов. [11] [12] Для реакции типа А + В—С → А—В + С удлинение длины вновь образовавшейся связи А—В определяется как R* AB = R AB − R. 0 AB , где R AB — длина связи A—B в переходном состоянии, а R 0 AB в молекуле продукта. Аналогично для связи, которая разрывается в реакции, R* BC = R BC − R. 0 до н.э. , где R 0 BC относится к молекуле реагента. [13]
Для экзотермических реакций ППЭ классифицируется как притягивающая (или ранняя нисходящая ), если R* AB > R* BC , так что переходное состояние достигается, когда реагенты приближаются друг к другу. После переходного состояния длина связи А—В продолжает уменьшаться, так что большая часть высвободившейся энергии реакции преобразуется в колебательную энергию связи А—В. [13] [14] Примером может служить гарпунная реакция K + Br 2 → K—Br + Br, в которой первоначальное дальнодействующее притяжение реагентов приводит к образованию активированного комплекса, напоминающего K + •••Br − •••Br. [13] Колебательно-возбужденные популяции молекул продукта можно обнаружить с помощью инфракрасной хемилюминесценции . [15] [16]
Напротив, ППЭ для реакции H + Cl 2 → HCl + Cl является отталкивающим (или поздним спуском ), поскольку R* HCl < R* ClCl и переходное состояние достигается при разделении продуктов. [13] [14] В этой реакции, в которой атом A (здесь H) легче атома B и C, энергия реакции высвобождается в основном в виде поступательной кинетической энергии продуктов. [13] Для такой реакции, как F + H 2 → HF + H, в которой атом A тяжелее B и C, происходит смешанное энерговыделение, как колебательное, так и поступательное, хотя ППЭ и отталкивающий. [13]
Для эндотермических реакций тип поверхности определяет тип энергии, который наиболее эффективен для проведения реакции. Поступательная энергия реагентов наиболее эффективна при инициировании реакций с притягивающей поверхностью, тогда как колебательное возбуждение (до более высокого колебательного квантового числа v) более эффективно для реакций с отталкивающей поверхностью. [13] В качестве примера последнего случая можно привести реакцию F + HCl(v=1) → Cl + HF примерно в пять раз быстрее, чем F + HCl(v=0) → Cl + HF при той же полной энергии HCl. [17]
История
[ редактировать ]Идея потенциальной энергетической поверхности химических реакций была впервые предложена французским физиком Рене Марселеном в 1913 году. [18] Первый полуэмпирический расчет поверхности потенциальной энергии был предложен для H + H 2 реакции Генри Эйрингом и Майклом Поланьи в 1931 году. Эйринг использовал поверхности потенциальной энергии для расчета констант скорости реакции в теории переходного состояния в 1935 году.
H + H 2 двумерный ПЭС
[ редактировать ]Поверхности потенциальной энергии обычно изображаются в виде трехмерных графиков, но они также могут быть представлены двумерными графиками, на которых развитие реакции изображается с помощью изоэнергетических линий.Коллинеарная система H + H 2 представляет собой простую реакцию, позволяющую легко и понятно построить двумерную ППЭ. В этой реакции атом водорода (Н) реагирует с молекулой диводорода (Н 2 ), образуя новую связь с одним атомом молекулы, что, в свою очередь, разрывает связь исходной молекулы. Это обозначается как H a + H b –H c → H a –H b + H c . Развитие реакции от реагентов (H+H₂) к продуктам (HHH), а также энергия частиц, участвующих в реакции, четко определены на соответствующей поверхности потенциальной энергии.Энергетические профили описывают потенциальную энергию как функцию геометрических переменных (PES в любом измерении не зависят от времени и температуры).
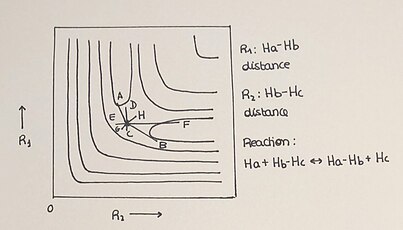
У нас есть различные соответствующие элементы в 2-D PES:
- Двумерный график показывает точки минимума, в которых мы находим реагенты , продукты и седловую точку или переходное состояние .
- Переходное состояние представляет собой максимум в координате реакции и минимум в координате, перпендикулярной пути реакции.
- Ход времени описывает траекторию каждой реакции. В зависимости от условий реакции процесс будет показывать разные пути достижения образования продукта, нанесенного на график между двумя осями.
См. также
[ редактировать ]- Вычислительная химия
- Минимизация энергии (или оптимизация геометрии)
- Энергетический профиль (химия)
- Потенциальная скважина
- Координата реакции
Ссылки
[ редактировать ]- ^ Поверхность потенциальной энергии (реакции) в Сборнике химической терминологии, 2-е изд. («Золотая книга»). Составлено А.Д. Макнотом и А. Уилкинсоном. Научные публикации Блэквелла, Оксфорд (1997)
- ^ Сато, С. (1955). «Новый метод построения поверхности потенциальной энергии». Бюллетень Химического общества Японии . 28 (7): 450–453. дои : 10.1246/bcsj.28.450 . Сато, Шин (1955). «О новом методе изображения поверхности потенциальной энергии». Журнал химической физики . 23 (3): 592–593. Бибкод : 1955ЖЧФ..23..592С . дои : 10.1063/1.1742043 .
- ^ Кейт Дж. Лейдлер , Химическая кинетика (3-е изд., Harper & Row 1987), стр.68-70 ISBN 0-06-043862-2
- ^ Стейнфельд Дж.И., Франциско Дж.С. и Хазе В.Л. Химическая кинетика и динамика (2-е изд., Prentice-Hall 1998), стр.201-2. ISBN 0-13-737123-3
- ^ Улучшенная интерполяция Шепарда с помощью метода наименьших квадратов с перемещением для методов быстрого марша и струн, Burger SK1, Liu Y, Sarkar U, Ayers PW, J Chem Phys. 2009 130(2) 024103. doi: 10.1063/1.2996579.
- ^ Чен, Шэньтан; Хо, Мин-Сюнь; Буллок, Р. Моррис; Дюбуа, Дэниел Л.; Дюпюи, Мишель; Руссо, Роджер; Раугей, Симона (2014). «Расчет ландшафтов свободной энергии: применение к электрокатализаторам на основе Ni с подвесными аминами для производства и окисления H2». АКС-катализ . 4 (1): 229–242. дои : 10.1021/cs401104w . ISSN 2155-5435 .
- ^ Уэльс, Дэвид Дж. (2004). Энергетические ландшафты: приложения к кластерам, биомолекулам и стеклам . Кембридж: Издательство Кембриджского университета . дои : 10.1017/CBO9780511721724 . ISBN 978-0-511-72172-4 .
- ^ Хойер, Андреас (2005). «Энергетические ландшафты. Применение к кластерам, биомолекулам и стеклам. Дэвид Дж. Уэльс». Angewandte Chemie, международное издание . 44 (12): 1756–1757. дои : 10.1002/anie.200485197 .
- ^ Баллард, Эндрю Дж.; Дас, Ританкар ; Мартиниани, Стефано; Мехта, Дагаш; Сагун, Левент; Стивенсон, Джейкоб Д.; Уэльс, Дэвид Дж. (2017). «Перспектива: энергетические ландшафты для машинного обучения». Физ. хим. хим. Физ . 19 (20): 12585–12603. arXiv : 1703.07915 . Бибкод : 2017PCCP...1912585B . дои : 10.1039/C7CP01108C . ПМИД 28367548 . S2CID 15326566 .
- ^ Энтони Коллинз Гамст; Уокер, Олден (2017). «Энергетический ландшафт простой нейронной сети». arXiv : 1706.07101 [ stat.ML ].
- ^ Привлекательная поверхность потенциальной энергии в Сборнике химической терминологии, 2-е изд. («Золотая книга»). Составлено А.Д. Макнотом и А. Уилкинсоном. Научные публикации Блэквелла, Оксфорд (1997)
- ^ Поверхность отталкивающей потенциальной энергии в Сборнике химической терминологии, 2-е изд. («Золотая книга»). Составлено А.Д. Макнотом и А. Уилкинсоном. Научные публикации Блэквелла, Оксфорд (1997)
- ^ Перейти обратно: а б с д и ж г Кейт Дж. Лейдлер , Химическая кинетика (3-е изд., Harper & Row 1987), стр. 461-8. ISBN 0-06-043862-2
- ^ Перейти обратно: а б Стейнфельд Дж.И., Франциско Дж.С. и Хазе В.Л. Химическая кинетика и динамика (2-е изд., Prentice-Hall, 1998), стр.272-4. ISBN 0-13-737123-3
- ^ Стейнфельд Дж.И., Франциско Дж.С. и Хазе В.Л. Химическая кинетика и динамика (2-е изд., Prentice-Hall 1998), стр.263 ISBN 0-13-737123-3
- ^ Аткинс П. и де Паула Дж. Физическая химия (8-е изд., WHFreeman 2006), стр.886 ISBN 0-7167-8759-8
- ^ Аткинс П. и де Паула Дж. Физическая химия (8-е изд., WHFreeman 2006), стр.889-890 ISBN 0-7167-8759-8
- ^ Вычислительная химия: Введение в теорию и приложения молекулярной и квантовой механики Эррол Г. Льюарс, 2-е изд. (Спрингер 2011) стр.21 ISBN 978-9048138616