Обратное взвешивание расстояния

Взвешивание обратного расстояния как сумма всех весовых функций для каждой точки выборки. Каждая функция имеет значение одной из выборок в своей точке выборки и нулевое значение в каждой другой точке выборки.

Взвешивание обратного расстояния ( IDW ) — это тип детерминированного метода многомерной интерполяции с известным разбросанным набором точек. Присвоенные значения неизвестным точкам рассчитываются с использованием средневзвешенного значения значений, доступных в известных точках. Этот метод также можно использовать для создания матриц пространственных весов в анализе пространственной автокорреляции (например, Морана I ).

Название, данное этому типу метода, было обусловлено применяемым средневзвешенным значением , поскольку при присвоении весов он использует обратную величину расстояния до каждой известной точки («степень близости»).

Определение проблемы

Ожидаемый результат — дискретное присвоение неизвестной функции. $u$ в регионе исследования:

$u(x):x\to \mathbb {R} ,\quad x\in \mathbf {D} \subset \mathbb {R} ^{n},$

где $\mathbf {D}$ является регионом исследования.

Набор $N$ известные точки данных можно описать как список кортежей :

$[(x_{1},u_{1}),(x_{2},u_{2}),...,(x_{N},u_{N})].$

Функция должна быть «гладкой» (непрерывной и однократно дифференцируемой), точнее ( $u(x_{i})=u_{i}$) и удовлетворить интуитивные ожидания пользователя относительно исследуемого явления. Более того, функция должна быть подходящей для компьютерного приложения по разумной цене (в настоящее время базовая реализация, вероятно, будет использовать параллельные ресурсы ).

Метод Шепарда

Историческая справка

Начиная с 1965 года в Гарвардской лаборатории компьютерной графики и пространственного анализа собралась разнообразная группа ученых, чтобы переосмыслить, среди прочего, то, что сейчас называется географическими информационными системами .

Движущая сила лаборатории, Говард Фишер , задумал улучшенную компьютерную картографическую программу, которую он назвал SYMAP, в которой с самого начала Фишер хотел улучшить интерполяцию. Он показал первокурсникам Гарвардского колледжа свою работу над SYMAP, и многие из них приняли участие в лабораторных мероприятиях. Один первокурсник, Дональд Шепард, решил пересмотреть интерполяцию в SYMAP, результатом чего стала его знаменитая статья 1968 года.

На алгоритм Шепарда также повлиял теоретический подход Уильяма Варнца и других сотрудников лаборатории, которые работали с пространственным анализом. Он провел ряд экспериментов с показателем степени расстояния, решив сделать что-то более близкое к модели гравитации (показатель -2). Шепард реализовал не только базовое взвешивание обратного расстояния, но также разрешил барьеры (проницаемые и абсолютные) для интерполяции.

В то время над интерполяцией работали другие исследовательские центры, особенно Канзасский университет и их программа SURFACE II. Тем не менее, возможности SYMAP были самыми современными, хотя и были запрограммированы студентом.

Основная форма

Интерполяция Шепарда для различных параметров мощности p по разбросанным точкам на поверхности $z=\exp(-x^{2}-y^{2})$

Учитывая набор точек выборки $\{\mathbf {x} _{i},u_{i}|{\text{for }}\mathbf {x} _{i}\in \mathbb {R} ^{n},u_{i}\in \mathbb {R} \}_{i=1}^{N}$, интерполяционная функция IDW $u(\mathbf {x} ):\mathbb {R} ^{n}\to \mathbb {R}$ определяется как:

$u(\mathbf {x} )={\begin{cases}{\dfrac {\sum _{i=1}^{N}{w_{i}(\mathbf {x} )u_{i}}}{\sum _{i=1}^{N}{w_{i}(\mathbf {x} )}}},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})\neq 0{\text{ for all }}i,\\u_{i},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})=0{\text{ for some }}i,\end{cases}}$

где

$w_{i}(\mathbf {x} )={\frac {1}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}$

— это простая весовая функция IDW, определенная Шепардом, x обозначает интерполируемую (произвольную) точку, x _i представляет собой интерполирующую (известную) точку, $d$ — заданное расстояние ( метрический оператор) от известной точки x _i до неизвестной точки x , N — общее количество известных точек, используемых при интерполяции, и $p$ – положительное действительное число, называемое параметром степени.

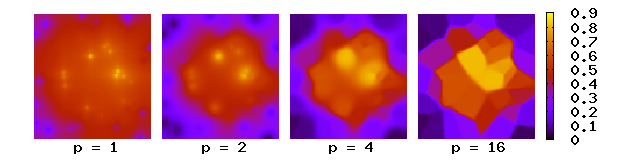
Здесь вес уменьшается по мере увеличения расстояния от интерполированных точек. Большие значения $p$ назначьте большее влияние значениям, ближайшим к интерполируемой точке, в результате чего результат превратится в мозаику из плиток ( диаграмма Вороного ) с почти постоянным интерполированным значением для больших значений p . Для двух измерений параметры мощности $p\leq 2$ приводят к тому, что в интерполируемых значениях преобладают точки, расположенные далеко, поскольку при плотности $\rho$ точек данных и соседних точек между расстояниями $r_{0}$ к $R$, суммарный вес составляет примерно

$\sum _{j}w_{j}\approx \int _{r_{0}}^{R}{\frac {2\pi r\rho \,dr}{r^{p}}}=2\pi \rho \int _{r_{0}}^{R}r^{1-p}\,dr,$

который расходится для $R\rightarrow \infty$ и $p\leq 2$. Для измерений M тот же аргумент справедлив и для $p\leq M$. При выборе значения p можно учитывать желаемую степень сглаживания при интерполяции, плотность и распределение интерполируемых выборок, а также максимальное расстояние, на котором отдельному образцу разрешено влиять на окружающие.

Метод Шепарда является следствием минимизации функционала, связанного с мерой отклонений между наборами интерполирующих точек { x , u } и i кортежами интерполируемых точек { x _i , u _i }, определяемыми как:

$\phi (\mathbf {x} ,u)=\left(\sum _{i=0}^{N}{\frac {(u-u_{i})^{2}}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}\right)^{\frac {1}{p}},$

полученное из условия минимизации:

${\frac {\partial \phi (\mathbf {x} ,u)}{\partial u}}=0.$

Этот метод легко распространить на другие размерные пространства и фактически представляет собой обобщение аппроксимации Лагранжа на многомерные пространства. Модифицированная версия алгоритма, предназначенная для трехмерной интерполяции, была разработана Робертом Дж. Ренка. и доступен в Netlib как алгоритм 661 в библиотеке TOMS .

Пример в 1 измерении

Интерполяция Шепарда в одном измерении, по 4 разбросанным точкам и с использованием p = 2.

Модифицированный метод Шепарда

Другая модификация метода Шепарда вычисляет интерполированное значение, используя только ближайших соседей внутри R -сферы (вместо полной выборки). В этом случае веса немного изменяются:

$w_{k}(\mathbf {x} )=\left({\frac {\max(0,R-d(\mathbf {x} ,\mathbf {x} _{k}))}{Rd(\mathbf {x} ,\mathbf {x} _{k})}}\right)^{2}.$

В сочетании со структурой быстрого пространственного поиска (например, kd-tree ) он становится эффективным методом интерполяции N log N, подходящим для крупномасштабных задач.

См. также

• Область (география)
• Модель гравитации
• Оценка плотности ядра
• Пространственный анализ
• Первый закон географии Тоблера
• Второй закон географии Тоблера