Молекулярная геометрия

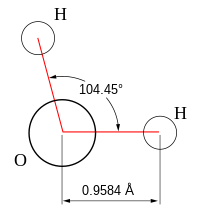
Молекулярная геометрия — это трехмерное расположение атомов , составляющих молекулу . Он включает в себя общую форму молекулы, а также длины связей , валентные углы , углы скручивания и любые другие геометрические параметры, которые определяют положение каждого атома.

Молекулярная геометрия влияет на несколько свойств вещества, включая его реакционную способность , полярность , фазу вещества , цвет , магнетизм и биологическую активность . ^[1]^[2]^[3] Углы между связями, образуемыми атомом, слабо зависят от остальной части молекулы, т. е. их можно понимать как приблизительно локальные и, следовательно, передаваемые свойства .

Определение [ править ]

Молекулярную геометрию можно определить различными спектроскопическими методами и дифракционными методами. ИК- , микроволновая и рамановская спектроскопия могут дать информацию о геометрии молекул на основе деталей колебательного и вращательного поглощения, обнаруженных этими методами. Рентгеновская кристаллография , дифракция нейтронов и дифракция электронов могут дать молекулярную структуру кристаллических твердых тел на основе расстояния между ядрами и концентрации электронной плотности. Газовую электронографию можно использовать для исследования малых молекул в газовой фазе. Методы ЯМР и FRET можно использовать для определения дополнительной информации, включая относительные расстояния, ^[4]^[5]^[6]двугранные углы, ^[7]^[8]углы и возможности подключения. Молекулярную геометрию лучше всего определять при низкой температуре, поскольку при более высоких температурах молекулярная структура усредняется по более доступным геометриям (см. следующий раздел). Более крупные молекулы часто существуют в нескольких стабильных геометриях ( конформационная изомерия ), которые близки по энергии на поверхности потенциальной энергии . Геометрию также можно вычислить с методами квантовой химии ab initio высокой точностью . Молекулярная геометрия может быть различной в твердом теле, растворе и газе.

Положение каждого атома определяется характером химических связей , которыми он соединен с соседними атомами. Молекулярную геометрию можно описать положениями этих атомов в пространстве, напоминая длины связей двух соединенных атомов, валентные углы трех связанных атомов и торсионные углы ( двугранные углы ) трех последовательных связей.

Влияние теплового возбуждения [ править ]

Поскольку движение атомов в молекуле определяется квантовой механикой, «движение» должно определяться квантовомеханическим способом. Общие (внешние) квантово-механические движения, трансляция и вращение, практически не меняют геометрию молекулы. (В некоторой степени вращение влияет на геометрию через силы Кориолиса и центробежные искажения , но для настоящего обсуждения это незначительно.) Помимо перемещения и вращения, третий тип движения — это молекулярная вибрация , которая соответствует внутренним движениям атомов, таким как как растяжение связи и изменение валентного угла. Молекулярные колебания гармоничны (по крайней мере, в хорошем приближении), и атомы колеблются около своих положений равновесия даже при абсолютном нуле температуры. При абсолютном нуле все атомы находятся в своем основном колебательном состоянии и демонстрируют нулевую точку квантовомеханического движения , так что волновая функция одной колебательной моды представляет собой не острый пик, а приблизительно гауссовую функцию (волновая функция для n = 0, изображенный в статье о квантовом гармоническом осцилляторе ). При более высоких температурах колебательные моды могут возбуждаться термически (в классической интерпретации это выражается утверждением, что «молекулы будут вибрировать быстрее»), но они все еще колеблются вокруг узнаваемой геометрии молекулы.

Чтобы понять вероятность того, что вибрация молекулы может быть термически возбуждена,мы проверяем фактор Больцмана β ≡ exp(− ΔE абсолютная / kT ) , где ΔE – энергия возбуждения колебательной моды, k – и постоянная Больцмана T – температура. При 298 К (25 °C) типичные значения фактора Больцмана β составляют:

β = 0,089 0 для Δ E = 0 500 см ⁻¹
β = 0,008 0 для Δ E = 1000 см ⁻¹
β = 0,0007 для Δ E = 1500 см ⁻¹.

( Обратный сантиметр — это энергетическая единица, которая обычно используется в инфракрасной спектроскопии ; 1 см ⁻¹ соответствует 1,239 84 × 10 ⁻⁴ эВ ). При энергии возбуждения 500 см ⁻¹, то около 8,9 процентов молекул подвергаются термическому возбуждению при комнатной температуре. Для сравнения: наименьшая энергия возбуждения в воде — это изгибная мода (около 1600 см). ⁻¹). Таким образом, при комнатной температуре менее 0,07 процента всех молекул данного количества воды будут колебаться быстрее, чем при абсолютном нуле.

Как говорилось выше, вращение практически не влияет на геометрию молекулы. Но как квантовомеханическое движение оно термически возбуждается при относительно (по сравнению с вибрацией) низких температурах. С классической точки зрения можно утверждать, что при более высоких температурах большее количество молекул будет вращаться быстрее.это означает, что они имеют более высокие угловую скорость и угловой момент . состояний с более высоким угловым моментом становится больше собственных На языке квантовой механики: с ростом температуры . Типичные энергии вращательного возбуждения составляют порядка нескольких см. ⁻¹. Результаты многих спектроскопических экспериментов расширяются, поскольку они включают усреднение по вращательным состояниям. Часто бывает трудно извлечь геометрию из спектров при высоких температурах, поскольку количество вращательных состояний, исследуемых при экспериментальном усреднении, увеличивается с ростом температуры. Таким образом, можно ожидать, что многие спектроскопические наблюдения дадут надежные молекулярные геометрии только при температурах, близких к абсолютному нулю, потому что при более высоких температурах слишком много более высоких вращательных состояний термически заселяются.

Связывание [ править ]

Молекулы по определению чаще всего удерживаются вместе ковалентными связями , включающими одинарные, двойные и/или тройные связи, где «связью» является общая пара электронов (другой метод связи между атомами называется ионной связью и включает в себя положительный катион и отрицательный анион ).

Молекулярную геометрию можно определить с точки зрения «длин связей», «углов связи» и «углов скручивания». Длина связи определяется как среднее расстояние между ядрами двух атомов, связанных вместе в любой данной молекуле. Валентный угол — это угол, образованный между тремя атомами по крайней мере через две связи. Для четырех атомов, связанных вместе в цепочку, угол скручивания — это угол между плоскостью, образованной первыми тремя атомами, и плоскостью, образованной тремя последними атомами.

Существует математическая связь между валентными углами для одного центрального атома и четырех периферийных атомов (обозначенных от 1 до 4), выраженная следующим определителем. Это ограничение лишает одну степень свободы выбора (изначально) шести свободных валентных углов, оставляя только пять вариантов валентных углов. (Углы θ ₁₁ , θ ₂₂ , θ ₃₃ и θ ₄₄ всегда равны нулю, и это соотношение можно изменить для различного количества периферийных атомов путем расширения/сжатия квадратной матрицы.)

0={\begin{vmatrix}\cos \theta _{11}&\cos \theta _{12}&\cos \theta _{13}&\cos \theta _{14}\\\cos \theta _{21}&\cos \theta _{22}&\cos \theta _{23}&\cos \theta _{24}\\\cos \theta _{31}&\cos \theta _{32}&\cos \theta _{33}&\cos \theta _{34}\\\cos \theta _{41}&\cos \theta _{42}&\cos \theta _{43}&\cos \theta _{44}\end{vmatrix}}

Молекулярная геометрия определяется квантовомеханическим поведением электронов. Используя приближение валентной связи, это можно понять по типу связей между атомами, составляющими молекулу. Когда атомы взаимодействуют с образованием химической связи , говорят, что атомные орбитали каждого атома объединяются в процессе, называемом орбитальной гибридизацией . Двумя наиболее распространенными типами связей являются сигма-связи (обычно образованные гибридными орбиталями) и пи-связи (образованные негибридизованными p-орбиталями атомов элементов основной группы ). Геометрию также можно понять с помощью теории молекулярных орбиталей, в которой электроны делокализованы.

Понимание волнового поведения электронов в атомах и молекулах является предметом квантовой химии .

Изомеры [ править ]

Изомеры — это типы молекул, которые имеют общую химическую формулу, но имеют разную геометрию, что приводит к различным свойствам:

вещество Чистое состоит только из одного типа изомеров молекулы (все они имеют одинаковую геометрическую структуру).
Структурные изомеры имеют одинаковую химическую формулу, но разное физическое расположение, часто образуя альтернативную молекулярную геометрию с совершенно разными свойствами. Атомы не связаны (соединены) вместе в одном и том же порядке.
- Функциональные изомеры — это особые виды структурных изомеров, в которых определенные группы атомов демонстрируют особое поведение, например эфир или спирт.
Стереоизомеры могут иметь множество схожих физико-химических свойств (точку плавления, температуру кипения) и в то же время весьма разную биохимическую активность. Это потому, что они демонстрируют рукоприкладство , которое обычно встречается в живых системах. Одним из проявлений этой хиральности или направленности является то, что они обладают способностью вращать поляризованный свет в разных направлениях.
Сворачивание белков связано со сложной геометрией и различными изомерами, которые белки . могут принимать

Типы молекулярной структуры [ править ]

Валентный угол — это геометрический угол между двумя соседними связями. Некоторые распространенные формы простых молекул включают:

Линейный : в линейной модели атомы соединены по прямой линии. Угол связи установлен на уровне 180°. Например, углекислый газ и оксид азота имеют линейную молекулярную форму.
Тригонально-плоские : Молекулы тригонально-плоской формы имеют несколько треугольную форму и находятся в одной плоскости (плоские) . Следовательно, валентные углы установлены равными 120°. Например, трифторид бора .
Угловые : Угловые молекулы (также называемые изогнутыми или V-образными ) имеют нелинейную форму. Например, вода (H ₂ O), имеющая угол около 105°. Молекула воды имеет две пары связанных электронов и две неподеленные неподеленные пары.
Тетраэдр : Тетра- означает четыре, а -эдр относится к грани твердого тела, поэтому « тетраэдр » буквально означает «имеющий четыре грани». Эта форма достигается, когда в одном центральном атоме имеется четыре связи без дополнительных неподеленных электронных пар. В соответствии с VSEPR (теорией отталкивания электронных пар валентной оболочки) валентные углы между электронными связями равны arccos (− 1/3 = 109,47 ) °. Например, метан (СН ₄ ) представляет собой тетраэдрическую молекулу.
Октаэдр : Окта- означает восемь, а -эдр относится к грани твердого тела, поэтому « октаэдр » означает «имеющий восемь граней». Угол связи составляет 90 градусов. Например, гексафторид серы (SF ₆ ) представляет собой октаэдрическую молекулу.
Тригонально-пирамидальная : молекула тригонально-пирамидальной формы имеет пирамидальную форму с треугольным основанием. В отличие от линейных и тригональных плоских форм, но похожих на тетраэдрическую ориентацию, пирамидальные формы требуют трех измерений, чтобы полностью разделить электроны. Здесь имеется только три пары связанных электронов, оставляя одну неподеленную неподеленную пару. Неподеленная пара - отталкивание пары связей изменяет угол связи с тетраэдрического угла на немного меньшее значение. ^[9] Например, аммиак (NH ₃ ).

Таблица ВСЕПР [ править ]

Валентные углы в таблице ниже представляют собой идеальные углы из простой теории VSEPR (произносится как «Теория Веспера»). ^{[ нужна ссылка ]}, за которым следует фактический угол для примера, приведенного в следующем столбце, где он отличается. Во многих случаях, таких как тригональная пирамида и изогнутая форма, фактический угол для примера отличается от идеального угла, а примеры отличаются на разную величину. Например, угол в H ₂ S (92°) отличается от тетраэдрического угла гораздо больше, чем угол в H ₂ O (104,48°).

Атомы, связанные с центральный атом	Одинокие пары	Электронные домены (стерическое число)	Форма	Идеальный угол соединения (валентный угол примера)	Пример
2	0	2	линейный	180°	СО ₂
3	0	3	тригональный плоский	120°	BF_БФ3
2	1	3	согнутый	120° (119°)	SO_SO2
4	0	4	четырехгранный	109.5°	СН ₄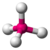
3	1	4	тригонально-пирамидальный	109.5° (106.8°) ^[10]	NH_NH3
2	2	4	согнутый	109.5° (104.48°) ^[11]^[12]	Н ₂ О
5	0	5	тригонально-бипирамидальный	90°, 120°	ПКл ₅
4	1	5	качели	топор-топор 180° (173,1°), экв–экв 120° (101,6°), ax–eq 90°	СФ ₄
3	2	5	Т-образный	90° (87.5°), 180° (175°)	КлФ ₃
2	3	5	линейный	180°	КсеФ ₂
6	0	6	октаэдрический	90°, 180°	СФ ₆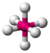
5	1	6	квадратно-пирамидальный	90° (84.8°)	БрФ ₅
4	2	6	квадратный плоский	90°, 180°	КсеФ ₄
7	0	7	пятиугольный бипирамидальный	90°, 72°, 180°	ЕСЛИ ₇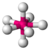
6	1	7	пятиугольный пирамидальный	72°, 90°, 144°	КсеОФ − 5
5	2	7	пятиугольный плоский	72°, 144°	ХеФ − 5
8	0	8	квадратный антипризматический		ХеФ 2− 8
9	0	9	трехгранный трехугольный призматический		РеХ 2- 9

3D-представления [ править ]

Линия или палка – атомные ядра не представлены, только связи в виде палочек или линий. Как и в двумерных молекулярных структурах этого типа, в каждой вершине подразумеваются атомы.

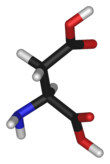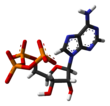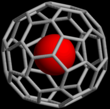График электронной плотности - показывает электронную плотность, определенную кристаллографически или с использованием квантовой механики, а не отдельные атомы или связи.

Шар и палка – атомные ядра представлены сферами (шариками), а связи – палочками.

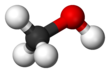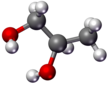Модели заполнения пространства или модели CPK (также схема раскраски атомов в представлениях) – молекула представлена перекрывающимися сферами, представляющими атомы.

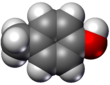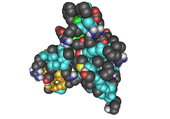Мультфильм – изображение, используемое для белков, где петли, бета-листы и альфа-спирали представлены схематически, а атомы или связи не представлены явно (например, основная цепь белка представлена в виде гладкой трубы).

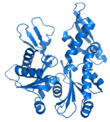Чем больше количество неподеленных пар содержится в молекуле, тем меньше углы между атомами этой молекулы. Теория VSEPR предсказывает, что неподеленные пары отталкивают друг друга, тем самым отталкивая от себя разные атомы.

См. также [ править ]

Ссылки [ править ]

^ Макмерри, Джон Э. (1992), Органическая химия (3-е изд.), Бельмонт: Уодсворт, ISBN 0-534-16218-5
^ Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Передовая неорганическая химия (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5
^ Александрос Хремос; Джек Ф. Дуглас (2015). «Когда разветвленный полимер становится частицей?» . Дж. Хим. Физ . 143 (11): 111104. Бибкод : 2015JChPh.143k1104C . дои : 10.1063/1.4931483 . ПМИД 26395679 .
^ Описание FRET. Архивировано 18 сентября 2008 г. на Wayback Machine.
^ Хиллиш, А; Лоренц, М; Дикманн, С. (2001). «Последние достижения в области FRET: определение расстояния в комплексах белок-ДНК». Современное мнение в области структурной биологии . 11 (2): 201–207. дои : 10.1016/S0959-440X(00)00190-1 . ПМИД 11297928 .
^ Введение в изображение FRET. Архивировано 14 октября 2008 г. в Wayback Machine.
^ получение двугранных углов из ³Константы связи J. Архивировано 7 декабря 2008 г. на Wayback Machine.
^ Еще одна константа связи ЯМР с двугранником, подобная Javascript. Архивировано 28 декабря 2005 г. на Wayback Machine.
^ Мисслер Г.Л. и Тарр Д.А. Неорганическая химия (2-е изд., Prentice-Hall 1999), стр.57-58.
^ Хейнс, Уильям М., изд. (2013). Справочник CRC по химии и физике (94-е изд.). ЦРК Пресс . стр. 9–26. ISBN 9781466571143 .
^ Хой, Арканзас; Бункер, PR (1979). «Точное решение уравнения Шредингера, изменяющего вращение, для трехатомной молекулы в применении к молекуле воды». Журнал молекулярной спектроскопии . 74 (1): 1–8. Бибкод : 1979JMoSp..74....1H . дои : 10.1016/0022-2852(79)90019-5 .
^ «CCCBDB Экспериментальные валентные углы, страница 2» . Архивировано из оригинала 3 сентября 2014 г. Проверено 27 августа 2014 г.

Внешние ссылки [ править ]

Учебное пособие по молекулярной геометрии и полярности 3D-визуализация молекул для определения полярности.
Молекулярная геометрия с использованием кристаллов. 3D-визуализация структуры молекул с использованием кристаллографии.

[1] Макмерри, Джон Э. (1992), Органическая химия (3-е изд.), Бельмонт: Уодсворт, ISBN 0-534-16218-5

[2] Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Передовая неорганическая химия (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5

[article0-3] Александрос Хремос; Джек Ф. Дуглас (2015). «Когда разветвленный полимер становится частицей?» . Дж. Хим. Физ . 143 (11): 111104. Бибкод : 2015JChPh.143k1104C . дои : 10.1063/1.4931483 . ПМИД 26395679 .

[4] Описание FRET. Архивировано 18 сентября 2008 г. на Wayback Machine.

[5] Хиллиш, А; Лоренц, М; Дикманн, С. (2001). «Последние достижения в области FRET: определение расстояния в комплексах белок-ДНК». Современное мнение в области структурной биологии . 11 (2): 201–207. дои : 10.1016/S0959-440X(00)00190-1 . ПМИД 11297928 .

[6] Введение в изображение FRET. Архивировано 14 октября 2008 г. в Wayback Machine.

[7] получение двугранных углов из ³Константы связи J. Архивировано 7 декабря 2008 г. на Wayback Machine.

[8] Еще одна константа связи ЯМР с двугранником, подобная Javascript. Архивировано 28 декабря 2005 г. на Wayback Machine.

[9] Мисслер Г.Л. и Тарр Д.А. Неорганическая химия (2-е изд., Prentice-Hall 1999), стр.57-58.

[CRC_94th-10] Хейнс, Уильям М., изд. (2013). Справочник CRC по химии и физике (94-е изд.). ЦРК Пресс . стр. 9–26. ISBN 9781466571143 .

[11] Хой, Арканзас; Бункер, PR (1979). «Точное решение уравнения Шредингера, изменяющего вращение, для трехатомной молекулы в применении к молекуле воды». Журнал молекулярной спектроскопии . 74 (1): 1–8. Бибкод : 1979JMoSp..74....1H . дои : 10.1016/0022-2852(79)90019-5 .

[12] «CCCBDB Экспериментальные валентные углы, страница 2» . Архивировано из оригинала 3 сентября 2014 г. Проверено 27 августа 2014 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

v т и Молекулярная геометрия
VSEPR theory Coordination number
Coordination number 2	Linear Bent
Coordination number 3	Trigonal planar Trigonal pyramidal T-shaped
Coordination number 4	Tetrahedral Square planar Seesaw
Coordination number 5	Trigonal bipyramidal Square pyramidal Pentagonal planar
Coordination number 6	Octahedral Trigonal prismatic Pentagonal pyramidal
Coordination number 7	Pentagonal bipyramidal Capped octahedral Capped trigonal prismatic
Coordination number 8	Square antiprismatic Dodecahedral Bicapped trigonal prismatic
Coordination number 9	Tricapped trigonal prismatic Capped square antiprismatic
Category

v т и Отрасли химии
Glossary of chemical formulae List of biomolecules List of inorganic compounds Periodic table
Analytical	Instrumental chemistry Electroanalytical methods Spectroscopy IR Raman UV-Vis NMR Mass spectrometry EI ICP MALDI Separation process Chromatography GC HPLC Crystallography Characterization Titration Wet chemistry Calorimetry Elemental analysis
Theoretical	Quantum chemistry Computational chemistry Mathematical chemistry Molecular modelling Molecular mechanics Molecular dynamics Molecular geometry VSEPR theory
Physical	Electrochemistry Spectroelectrochemistry Photoelectrochemistry Thermochemistry Chemical thermodynamics Surface science Interface and colloid science Micromeritics Cryochemistry Sonochemistry Structural chemistry Chemical physics Molecular physics Femtochemistry Chemical kinetics Spectroscopy Photochemistry Spin chemistry Microwave chemistry Equilibrium chemistry Mechanochemistry
Inorganic	Coordination chemistry Magnetochemistry Organometallic chemistry Organolanthanide chemistry Cluster chemistry Solid-state chemistry Ceramic chemistry
Organic	Stereochemistry Alkane stereochemistry Physical organic chemistry Organic reactions Organic synthesis Retrosynthetic analysis Enantioselective synthesis Total synthesis / Semisynthesis Fullerene chemistry Polymer chemistry Petrochemistry Dynamic covalent chemistry
Biological	Biochemistry Molecular biology Cell biology Chemical biology Bioorthogonal chemistry Medicinal chemistry Pharmacology Clinical chemistry Neurochemistry Bioorganic chemistry Bioorganometallic chemistry Bioinorganic chemistry Biophysical chemistry
Interdisciplinarity	Nuclear chemistry Radiochemistry Radiation chemistry Actinide chemistry Cosmochemistry / Astrochemistry / Stellar chemistry Geochemistry Biogeochemistry Photogeochemistry Environmental chemistry Atmospheric chemistry Ocean chemistry Clay chemistry Carbochemistry Food chemistry Carbohydrate chemistry Food physical chemistry Agricultural chemistry Soil chemistry Chemistry education Amateur chemistry General chemistry Clandestine chemistry Forensic chemistry Forensic toxicology Post-mortem chemistry Nanochemistry Supramolecular chemistry Chemical synthesis Green chemistry Click chemistry Combinatorial chemistry Biosynthesis Chemical engineering Stoichiometry Materials science Metallurgy Ceramic engineering Polymer science
See also	History of chemistry Nobel Prize in Chemistry Timeline of chemistry of element discoveries "The central science" Chemical reaction Catalysis Chemical element Chemical compound Atom Molecule Ion Chemical substance Chemical bond Alchemy Quantum mechanics
Category Commons Portal WikiProject