Теория ВСЕПР
электронных пар валентной оболочки ( VSEPR ) Теория ( / ˈ v ɛ s p ər , və ˈ s ɛ p ər / отталкивания VESP -ər , [1] : 410 и- СЭП -муж [2] ) — это модель , используемая в химии для предсказания геометрии отдельных молекул по количеству электронных пар, окружающих их центральные атомы. [3] Ее также называют теорией Гиллеспи-Нихолма в честь двух ее главных разработчиков, Рональда Гиллеспи и Рональда Нихолма .
Предпосылка VSEPR заключается в том, что пары валентных электронов, окружающие атом, имеют тенденцию отталкивать друг друга. Чем больше отталкивание, тем выше энергия (менее стабильна) молекула. молекулы , предсказанная VSEPR, Следовательно, молекулярная геометрия — это такая геометрия молекулы, в которой это отталкивание минимально возможно. Гиллеспи подчеркивал, что электрон-электронное отталкивание, обусловленное принципом Паули, более важно в определении молекулярной геометрии, чем электростатическое отталкивание . [4]
Идея теории VSEPR основана на топологическом анализе электронной плотности молекул. К таким методам квантово-химической топологии (ККТ) относятся функция локализации электрона (ELF) и квантовая теория атомов в молекулах (AIM или QTAIM). [4] [5]
История [ править ]
Идея корреляции между молекулярной геометрией и количеством пар валентных электронов (как общих, так и неподеленных) была первоначально предложена в 1939 году Рютаро Цучида в Японии. [6] и был независимо представлен на Бейкеровской лекции в 1940 году Невилом Сиджвиком и Гербертом Пауэллом из Оксфордского университета . [7] В 1957 году Рональд Гиллеспи и Рональд Сидней Нихолм из Университетского колледжа Лондона усовершенствовали эту концепцию до более подробной теории, позволяющей выбирать между различными альтернативными геометриями. [8] [9]
Обзор [ править ]
Теория VSEPR используется для предсказания расположения электронных пар вокруг центральных атомов в молекулах, особенно в простых и симметричных молекулах. Центральный атом определяется в этой теории как атом, который связан с двумя или более другими атомами, тогда как концевой атом связан только с одним другим атомом. [1] : 398 Например, в молекуле метилизоцианата (H 3 C-N=C=O) два углерода и один азот являются центральными атомами, а три водорода и один кислород - концевыми атомами. [1] : 416 Геометрия центральных атомов и их несвязывающих электронных пар, в свою очередь, определяет геометрию более крупной молекулы.
Число электронных пар в валентной оболочке центрального атома определяется после рисования структуры Льюиса молекулы и ее расширения, чтобы показать все связывающие группы и неподеленные пары электронов. [1] : 410–417 В теории VSEPR двойная или тройная связь рассматривается как одинарная связующая группа. [1] Сумма числа атомов, связанных с центральным атомом, и количества неподеленных пар, образованных его несвязывающими валентными электронами, известна как стерическое число центрального атома.
Предполагается, что электронные пары (или группы, если присутствуют кратные связи) лежат на поверхности сферы с центром в центральном атоме и стремятся занять положения, которые минимизируют их взаимное отталкивание за счет максимального увеличения расстояния между ними. [1] : 410–417 [10] Таким образом, количество электронных пар (или групп) определяет общую геометрию, которую они примут. Например, когда центральный атом окружают две пары электронов, их взаимное отталкивание минимально, когда они лежат на противоположных полюсах сферы. Следовательно, ожидается, что центральный атом примет линейную геометрию. Если центральный атом окружают 3 пары электронов, их отталкивание минимизируется за счет размещения их в вершинах равностороннего треугольника с центром на атоме. Следовательно, предсказанная геометрия является тригональной . Аналогично, для 4 пар электронов оптимальным расположением является тетраэдрическое . [1] : 410–417
В качестве инструмента прогнозирования геометрии, принятой с заданным числом электронных пар, часто используемая физическая демонстрация принципа минимального отталкивания электронных пар использует надутые воздушные шары. В результате манипуляций воздушные шары приобретают небольшой поверхностный электростатический заряд, что приводит к принятию примерно той же геометрии, когда они связаны вместе на своих ножках, как и соответствующее количество электронных пар. Например, пять связанных вместе шариков принимают тригонально-бипирамидальную геометрию, как и пять связующих пар молекулы PCl 5 .
Стерическое число [ править ]
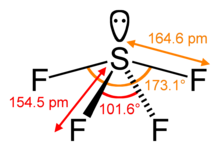
Стерическое число центрального атома в молекуле — это количество атомов, связанных с этим центральным атомом, называемое его координационным числом , плюс количество неподеленных пар валентных электронов на центральном атоме. [11] В молекуле SF 4 , например, центральный атом серы имеет четыре лиганда ; координационное число серы равно четырем. Помимо четырех лигандов, сера в этой молекуле имеет еще одну неподеленную пару. Таким образом, стерическое число равно 4 + 1 = 5.
Степень отталкивания [ править ]
Общая геометрия дополнительно уточняется за счет разделения связывающих и несвязывающих электронных пар. Связывающая пара электронов, образующая сигма-связь с соседним атомом, находится дальше от центрального атома, чем несвязывающая (неподеленная) пара этого атома, которая удерживается близко к его положительно заряженному ядру. Таким образом, теория VSEPR считает, что отталкивание неподеленной пары больше, чем отталкивание связывающей пары. Таким образом, когда молекула имеет два взаимодействия с разной степенью отталкивания, теория VSEPR предсказывает структуру, в которой неподеленные пары занимают положения, которые позволяют им испытывать меньшее отталкивание. Отталкивания одинокая пара-неподеленная пара (lp-lp) считаются более сильными, чем отталкивания одинокая пара-связывающая пара (lp-bp), которые, в свою очередь, считаются более сильными, чем отталкивания связывающая пара-связывающая пара (bp-bp), различия, которые затем определяют решения относительно общей геометрии, когда возможны 2 или более неэквивалентных позиций. [1] : 410–417 Например, когда 5 пар валентных электронов окружают центральный атом, они принимают тригонально-бипирамидальную молекулярную геометрию с двумя коллинеарными осевыми положениями и тремя экваториальными положениями. Электронная пара в аксиальном положении имеет трех близких экваториальных соседей, находящихся всего на расстоянии 90°, и четвертого, намного дальше, на расстоянии 180°, в то время как экваториальная электронная пара имеет только две соседние пары на расстоянии 90° и две на расстоянии 120°. Отталкивание от ближайших соседей под углом 90° более важно, так что осевые позиции испытывают большее отталкивание, чем экваториальные; следовательно, когда есть неподеленные пары, они имеют тенденцию занимать экваториальные положения, как показано на диаграммах следующего раздела для стерического номера пять. [10]
Разницу между неподеленными парами и связующими парами также можно использовать для объяснения отклонений от идеализированной геометрии. Например, молекула H 2 O имеет в своей валентной оболочке четыре пары электронов: две неподеленные пары и две пары связей. Четыре пары электронов разбросаны так, что они направлены примерно к вершинам тетраэдра. Однако валентный угол между двумя связями O–H составляет всего 104,5 °, а не 109,5 °, как в правильном тетраэдре, поскольку две неподеленные пары (чьи оболочки плотности или вероятности лежат ближе к ядру кислорода) оказывают большее взаимное отталкивание. чем две пары облигаций. [1] : 410–417 [10]
Связь более высокого порядка также оказывает большее отталкивание, поскольку вносят свой вклад электроны пи-связи . [10] Например, в изобутилене (H 3 C) 2 C=CH 2 угол H 3 C-C=C (124°) больше, чем угол H 3 C-C-CH 3 (111,5°). Однако в карбонат- ионе CO 2−
3 , все три связи C-O эквивалентны с углами 120° из-за резонанса .
Метод AX [ править ]
«Метод AXE» подсчета электронов обычно используется при применении теории VSEPR. Электронные пары вокруг центрального атома представлены формулой AX n E m , где A представляет центральный атом и всегда имеет подразумеваемый нижний индекс. Каждый X представляет собой лиганд (атом, связанный с A). Каждый E представляет собой неподеленную пару электронов центрального атома. [1] : 410–417 Общее количество X и E известно как стерическое число. Например, в молекуле AX 3 E 2 атом A имеет стерическое число 5.
Когда атомы заместителя (X) не все одинаковы, геометрия все еще приблизительно верна, но валентные углы могут немного отличаться от тех, где все внешние атомы одинаковы. Например, атомы углерода двойной связи в алкенах, таких как C 2 H 4 , имеют вид AX 3 E 0 , но не все валентные углы составляют точно 120°. Аналогично SOCl 2 представляет собой AX 3 E 1 , но поскольку заместители X не идентичны, углы X-A-X не все равны.
На основании стерического числа и распределения X и E теория VSEPR делает предсказания в следующих таблицах.
Элементы основной группы [ править ]
Для элементов основной группы существуют стереохимически активные неподеленные пары E , число которых может варьироваться от 0 до 3. Обратите внимание, что геометрия названа только в соответствии с положениями атомов, а не расположением электронов. Например, описание AX 2 E 1 как изогнутой молекулы означает, что три атома AX 2 не лежат на одной прямой, хотя неподеленная пара помогает определить геометрию.
| Стерик число | Молекулярная геометрия [12] 0 одиноких пар | Молекулярная геометрия [1] : 413–414 1 одинокая пара | Молекулярная геометрия [1] : 413–414 2 одинокие пары | Молекулярная геометрия [1] : 413–414 3 одинокие пары |
|---|---|---|---|---|
| 2 | ||||
| 3 |  |  | ||
| 4 | 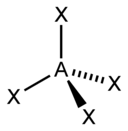 |  |  | |
| 5 |  | 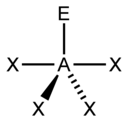 |  |  |
| 6 | 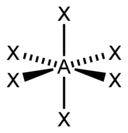 |  |  | |
| 7 |  | 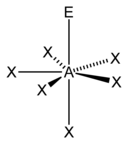 | 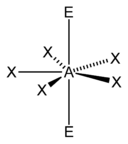 | |
| 8 |
| Молекула тип | Молекулярная форма [1] : 413–414 | Электронное расположение [1] : 413–414 включая одиночные пары, показаны желтым цветом | Геометрия [1] : 413–414 исключая одинокие пары | Примеры |
|---|---|---|---|---|
| АКС 2 Е 0 | Линейный | БеСl 2 , [3] СО 2 [10] | ||
| АКС 2 Е 1 | Бент |  |  | НЕТ − 2 , [3] СО2 , [1] : 413–414 О3 , [3] ССl 2 |
| ТОПОР 2 Е 2 | Бент | 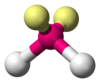 |  | Н 2 О , [1] : 413–414 ИЗ 2 [13] : 448 |
| ТОПОР 2 Е 3 | Линейный |  | ХеФ 2 , [1] : 413–414 я − 3 , [13] : 483 ХеСl 2 | |
| АКС 3 Е 0 | Тригональная плоская |  |  | БФ3 , [1] : 413–414 СО 2− 3 , [13] : 368 СН 2 О , НЕТ − 3 , [3] SOSO3 [10] |
| ТОПОР 3 Е 1 | Трехугольная пирамидальная |  |  | НХ3 , [1] : 413–414 ПКл 3 [13] : 407 |
| ТОПОР 3 Е 2 | Т-образный |  |  | КлФ 3 , [1] : 413–414 BrFБрФ3 [13] : 481 |
| АКС 4 Е 0 | Тетраэдрический | 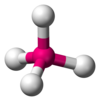 |  | СН 4 , [1] : 413–414 PO 3− 4 , ТАК 2− 4 , [10] ClO − 4 , [3] КсеО 4 [13] : 499 |
| АКС 4 Е 1 | Качели или дисфеноидальные |  | 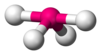 | СФ 4 [1] : 413–414 [13] : 45 |
| ТОПОР 4 Е 2 | Квадратный плоский |  |  | КсеФ 4 [1] : 413–414 |
| АКС 5 Е 0 | Треугольная бипирамида |  |  | ПКл 5 , [1] : 413–414 ПФ 5 , [1] : 413–414 |
| АКС 5 Е 1 | Квадратно-пирамидальный | 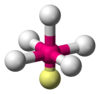 |  | КлФ 5 , [13] : 481 БрФ 5 , [1] : 413–414 КсеОФ 4 [10] |
| ТОПОР 5 Е 2 | Пятиугольная плоская |  |  | XeF − 5 [13] : 498 |
| АКС 6 Е 0 | Октаэдрический | 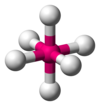 |  | СФ 6 [1] : 413–414 |
| АКС 6 Е 1 | Пятиугольная пирамидальная |  |  | XeOF − 5 , [14] ИОФ 2− 5 [14] |
| АКС 7 Е 0 | Пятиугольная бипирамида [10] |  |  | ЕСЛИ 7 [10] |
| АКС 8 Е 0 | Квадратный антипризматический [10] |  |  | ЕСЛИ − 8 , ХеФ 8 2- в (НО) 2 XeF 8 |
Переходные металлы ( Кеперта модель )
Неподеленные пары атомов переходных металлов обычно стереохимически неактивны, а это означает, что их присутствие не меняет геометрию молекулы. Например, гексааво-комплексы M(H 2 O) 6 все октаэдрические при M = V 3+ , Мн 3+ , Ко 3+ , Является 2+ и цинк 2+ , несмотря на то, что электронные конфигурации центрального иона металла d 2 , д 4 , д 6 , д 8 и д 10 соответственно. [13] : 542 Модель Кеперта игнорирует все неподеленные пары атомов переходных металлов, так что геометрия вокруг всех таких атомов соответствует геометрии VSEPR для AX n с 0 неподеленными парами E. [15] [13] : 542 Его часто пишут ML n , где M = металл и L = лиганд. Модель Кеперта предсказывает следующую геометрию для координационных чисел от 2 до 9:
| Молекула тип | Форма | Геометрия | Примеры |
|---|---|---|---|
| МЛ 2 | Линейный | HgCl 2 [3] | |
| МЛ 3 | Тригональная плоская |  | |
| MLML4 | Тетраэдрический |  | NiCl 2− 4 |
| МЛ 5 | Треугольная бипирамида |  | Fe(CO) 5 |
| Квадратно-пирамидальный |  | MnClMnCl5 2− | |
| МЛ 6 | Октаэдрический |  | ВК 6 [13] : 659 |
| МЛ 7 | Пятиугольная бипирамида [10] |  | ЗрФ 3− 7 |
| Закрытый октаэдр |  | МФ − 7 | |
| Треугольно-призматический с крышкой | 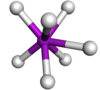 | Выключенный 2− 7 | |
| МЛ 8 | Квадратный антипризматический [10] |  | РеФ − 8 |
| Додекаэдрический |  | Мо(CN) 4− 8 | |
| Двуглавая треугольная призматика | 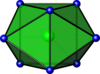 | ЗрФ 4− 8 | |
| МЛ 9 | Трехглавая треугольная призматика | 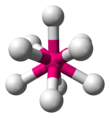 | РеХ 2− 9 [13] : 254 |
| Квадратный антипризматический с крышкой |  |
Примеры [ править ]
Молекула метана (CH 4 ) тетраэдрическая, поскольку имеет четыре пары электронов. Четыре атома водорода расположены в вершинах тетраэдра , а валентный угол равен cos. −1 (− 1 ⁄ 3 ) ≈ 109° 28′. [16] [17] Это называется молекулой типа AX 4 . Как упоминалось выше, A представляет собой центральный атом, а X представляет собой внешний атом. [1] : 410–417
Молекула аммиака (NH 3 ) имеет три пары электронов, участвующих в связывании, но на атоме азота имеется неподеленная пара электронов. [1] : 392–393 Он не связан с другим атомом; однако он влияет на общую форму посредством отталкивания. Как и в случае с метаном, описанным выше, существует четыре области электронной плотности. Следовательно, общая ориентация областей электронной плотности тетраэдрическая. С другой стороны, внешних атомов всего три. Ее называют молекулой типа AX 3 E, поскольку неподеленная пара представлена буквой E. [1] : 410–417 По определению, форма или геометрия молекулы описывает только геометрическое расположение атомных ядер, которое для NH 3 является тригонально-пирамидальным . [1] : 410–417
Возможны стерические числа 7 и выше, но они встречаются реже. Стерическое число 7 встречается в гептафториде йода (IF 7 ); базовая геометрия для стерического числа 7 — пятиугольная бипирамида. [10] Наиболее распространенной геометрией для стерического числа 8 является квадратная антипризматическая геометрия. [18] : 1165 Примеры этого включают октацианомолибдат ( Mo (CN) 4−
8 ) и октафторцирконат ( ZrF 4−
8 ) анионы. [18] : 1165 Нонагидридоренат-ион ( ReH 2−
9 ) в нонагидридоренате калия представляет собой редкий пример соединения со стерическим числом 9, имеющего трехгранную тригонально-призматическую геометрию. [13] : 254 [18]
Стерические числа больше 9 очень редки, и неясно, какая геометрия обычно предпочтительна. [19] Возможными геометриями для стерических чисел 10, 11, 12 или 14 являются двуглавый квадратный антипризматический (или двуглавый додекадельтаэдр ), октадекаэдр , икосаэдр и двуглавый шестиугольный антипризматический соответственно. Соединений с таким высоким стерическим числом, включающих монодентатные лиганды, не существует, а соединения, включающие мультидентатные лиганды, часто можно анализировать более просто как комплексы с более низкими стерическими числами, когда некоторые полидентатные лиганды рассматриваются как единое целое. [18] : 1165, 1721
Исключения [ править ]
Существуют группы соединений, в которых VSEPR не может предсказать правильную геометрию.
AX 2 E 0 Некоторые молекулы [ править ]
Было рассчитано, что формы более тяжелых аналогов алкинов элемента 14-й группы (RM≡MR, где M = Si, Ge, Sn или Pb) изогнуты. [20] [21] [22]
AX 2 E 2 Некоторые молекулы [ править ]
Одним из примеров геометрии AX 2 E 2 является молекулярный оксид лития Li 2 O, линейная, а не изогнутая структура, которая объясняется тем, что его связи являются по существу ионными и что приводит к сильному отталкиванию лития-лития. [23] Другим примером является O(SiH 3 ) 2 с углом Si-O-Si 144,1°, что сравнимо с углами в Cl 2 O (110,9°), (CH 3 ) 2 O (111,7°) и N(CH 3 ) 3 (110,9°). [24] Гиллеспи и Робинсон рационализируют валентный угол Si-O-Si на основе наблюдаемой способности неподеленной пары лиганда наиболее сильно отталкивать другие электронные пары, когда электроотрицательность лиганда больше или равна электроотрицательности центрального атома. [24] В O(SiH 3 ) 2 центральный атом более электроотрицательен, а неподеленные пары менее локализованы и менее отталкивающи. Больший валентный угол Si-O-Si является результатом этого, а также сильного отталкивания лиганд-лиганд со стороны относительно большого лиганда -SiH 3 . [24] Берфорд и др. с помощью рентгеновских дифракционных исследований показали, что Cl 3 Al-O-PCl 3 имеет линейный валентный угол Al-O-P и, следовательно, не является молекулой VSEPR. [25]
AX 6 E 1 AX 8 E 1 молекулы Некоторые и

Некоторые молекулы AX 6 E 1 , например гексафторид ксенона (XeF 6 ) и анионы Te(IV) и Bi(III), TeCl 2−
6 , ТеБр 2−
6 , БиСл 3−
6 , БиБр 3−
6 и БИИ 3−
6 , представляют собой октаэдрические, а не пятиугольные пирамиды, и неподеленная пара не влияет на геометрию в той степени, которую предсказывает VSEPR. [26] Аналогично октафтороксенат-ион ( XeF 2−
8 ) в октафтороксенате(VI) нитрозония [13] : 498 [27] [28] представляет собой квадратную антипризму с минимальными искажениями, несмотря на наличие неподеленной пары. Одно из объяснений состоит в том, что стерическое скучивание лигандов практически не оставляет места для несвязывающей неподеленной пары; [24] Еще одно объяснение — эффект инертной пары . [13] : 214
МЛ 4 Квадратно-плоскостные комплексы [ править ]
Модель Кеперта предсказывает, что молекулы переходного металла ML 4 имеют тетраэдрическую форму, и не может объяснить образование плоских квадратных комплексов. [13] : 542 Большинство таких комплексов имеют рекламу. 8 конфигурация, как у тетрахлорплатината ( PtCl 2−
4 ) ион. Объяснение формы плоских квадратных комплексов связано с электронными эффектами и требует использования теории кристаллического поля . [13] : 562–4
с сильным d вкладом - Комплексы

Некоторые комплексы переходных металлов с низким числом d-электронов имеют необычную геометрию, которую можно объяснить связующим взаимодействием d-подоболочки. [29] Гиллеспи обнаружил, что это взаимодействие создает пары связей, которые также занимают соответствующие антиподальные точки (лиганды напротив) сферы. [30] [4] Это явление представляет собой электронный эффект, возникающий из-за двухдольной формы лежащего в основе sd. х гибридные орбитали . [31] [32] Отталкивание этих связывающих пар приводит к появлению другого набора форм.
| Тип молекулы | Форма | Геометрия | Примеры |
|---|---|---|---|
| МЛ 2 | Бент |  | ТиО 2 [29] |
| МЛ 3 | Трехугольная пирамидальная |  | КрО 3 [33] |
| MLML4 | Тетраэдрический |  | ТиСl 4 [13] : 598–599 |
| МЛ 5 | Квадратно-пирамидальный |  | Та(СН 3 ) 5 [34] |
| МЛ 6 | C 3v Треугольно-призматический |  | Вт( СН3 ) 6 [35] |
Газофазные структуры трехатомных галогенидов более тяжелых членов группы 2 (т.е. галогениды кальция, стронция и бария, MX 2 ) не являются линейными, как предполагалось, а изогнуты (приблизительные углы X–M–X: CaF 2 120 SrF 2 ; SrCl 2 130 ° ° BaBr ; 2 115 ; ° [36] предположил Гиллеспи , что это также вызвано связующим взаимодействием лигандов с подоболочкой d атома металла, что влияет, таким образом, на геометрию молекулы. [24] [37]
Сверхтяжелые элементы [ править ]
Предполагается, что релятивистские эффекты на электронных орбиталях сверхтяжелых элементов будут влиять на молекулярную геометрию некоторых соединений. Например, электроны 6d 5/2 в нихонии играют неожиданно сильную роль в связывании, поэтому NhF 3 должен принять Т-образную геометрию, а не тригональную плоскую геометрию, как у его более легкого родственника BF 3 . [38] Напротив, согласно прогнозам, дополнительная стабильность электронов 7p 1/2 в теннессине сделает TsF 3 тригонально-планарным, в отличие от Т-образной геометрии, наблюдаемой для IF 3 и предсказанной для At F 3 ; [39] аналогично, Og F 4 должен иметь тетраэдрическую геометрию, в то время как XeF 4 имеет плоскую квадратную геометрию, и Rn F 4 , по прогнозам, будет иметь такую же геометрию. [40]
Молекулы с нечетными электронами [ править ]
Теорию VSEPR можно распространить на молекулы с нечетным числом электронов, рассматривая неспаренный электрон как «полуэлектронную пару» - например, Гиллеспи и Найхолм. [8] : 364–365 предположили, что уменьшение валентного угла в ряду NO +
2 (180°), НЕТ 2 (134°), НЕТ −
2 (115°) указывает на то, что данный набор пар связывающих электронов оказывает более слабое отталкивание на одиночный несвязывающий электрон, чем на пару несвязывающих электронов. По сути, они рассматривали диоксид азота как молекулу AX 2 E 0,5 с промежуточной геометрией между NO +
2 и НЕТ −
2 . Точно так же диоксид хлора (ClO 2 ) представляет собой молекулу AX 2 E 1,5 с промежуточной геометрией между ClO +
2 и ClO −
2 . [ нужна ссылка ]
Наконец, метильный радикал (CH 3 прогнозируется, что ) будет тригонально-пирамидальным, как и метиловый анион ( CH −
3 ), но с большим валентным углом (как в тригональном плоском метил-катионе ( CH +
3 )). Однако в этом случае предсказание VSEPR не совсем верно, поскольку CH 3 на самом деле является плоским, хотя его искажение до пирамидальной геометрии требует очень мало энергии. [41]
См. также [ править ]
- Правило Бента (эффект электроотрицательности лиганда)
- Сравнение программного обеспечения для моделирования молекулярной механики
- Линейная комбинация атомных орбиталей
- Молекулярная геометрия
- Молекулярное моделирование
- Теория молекулярных орбиталей (МОТ)
- Задача Томсона
- Теория валентной связи (VBT)
- Формула взаимодействия валентностей
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но из в Петруччи, Р.Х.; WS, Харвуд; ФГ, Сельдь (2002). Общая химия: принципы и современные приложения (8-е изд.). Прентис-Холл. ISBN 978-0-13-014329-7 .
- ^ Стокер, Х. Стивен (2009). Общая, органическая и биологическая химия . Cengage Обучение. п. 119. ИСБН 978-0-547-15281-3 .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г Джолли, WL (1984). Современная неорганическая химия . МакГроу-Хилл. стр. 77–90 . ISBN 978-0-07-032760-3 .
- ↑ Перейти обратно: Перейти обратно: а б с Гиллеспи, Р.Дж. (2008). «Пятьдесят лет модели ВСЕПР». Коорд. хим. Преподобный . 252 (12–14): 1315–1327. дои : 10.1016/j.ccr.2007.07.007 .
- ^ Бадер, Ричард Ф.В.; Гиллеспи, Рональд Дж.; Макдугалл, Престон Дж. (1988). «Физическая основа модели молекулярной геометрии VSEPR». Дж. Ам. хим. Соц . 110 (22): 7329–7336. дои : 10.1021/ja00230a009 .
- ^ Цучида, Рютаро (1939). «Новая простая теория валентности» Новая простая теория атомной валентности [Новая теория простой валентности]. Ниппон Кагаку Кайши (на японском языке). 60 (3): 245–256. дои : 10.1246/nikkashi1921.60.245 .
- ^ Сиджвик, Невада; Пауэлл, HM (1940). «Бейкеровская лекция. Стереохимические типы и валентные группы» . Учеб. Р. Сок. А. 176 (965): 153–180. Бибкод : 1940RSPSA.176..153S . дои : 10.1098/rspa.1940.0084 .
- ↑ Перейти обратно: Перейти обратно: а б Гиллеспи, Р.Дж. ; Нихольм, Р.С. (1957). «Неорганическая стереохимия». Q. Преподобный Chem. Соц . 11 (4): 339. doi : 10.1039/QR9571100339 .
- ^ Гиллеспи, Р.Дж. (1970). «Модель отталкивания электронных пар для молекулярной геометрии». Дж. Хим. Образование . 47 (1): 18. Бибкод : 1970ЖЧЭд..47...18Г . дои : 10.1021/ed047p18 .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л м н Мисслер, Г.Л.; Тарр, Д.А. (1999). Неорганическая химия (2-е изд.). Прентис-Холл. стр. 54–62. ISBN 978-0-13-841891-5 .
- ^ Мисслер, Г.Л.; Тарр, Д.А. (1999). Неорганическая химия (2-е изд.). Прентис-Холл. п. 55. ИСБН 978-0-13-841891-5 .
- ^ Петруччи, Р.Х.; WS, Харвуд; ФГ, Сельдь (2002). Общая химия: принципы и современные приложения (8-е изд.). Прентис-Холл. С. 413–414 (табл. 11.1). ISBN 978-0-13-014329-7 .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л м н тот п д р с Хаускрофт, CE; Шарп, AG (2005). Неорганическая химия (2-е изд.). Пирсон. ISBN 978-0-130-39913-7 .
- ↑ Перейти обратно: Перейти обратно: а б Баран, Э. (2000). «Средние амплитуды колебаний пятиугольно-пирамидального XeOF −
5 и ИОФ 2−
5 анионов». J. Fluorine Chem . 101 : 61–63. doi : 10.1016/S0022-1139(99)00194-3 . - ^ Андерсон, ОП (1983). «Рецензии на книгу: Неорганическая стереохимия (Дэвид Л. Кеперт)» (PDF) . Акта Кристаллографика Б. 39 : 527–528. дои : 10.1107/S0108768183002864 . Проверено 14 сентября 2020 г.
основанный на систематическом количественном применении общих представлений об отталкивании электронных пар.
- ^ Бриттин, МЫ (1945). «Валентный угол тетраэдрического атома углерода». Дж. Хим. Образование . 22 (3): 145. Бибкод : 1945ЖЧЭд..22..145Б . дои : 10.1021/ed022p145 .
- ^ «Угол между двумя ветвями тетраэдра». Архивировано 3 октября 2018 г. в Wayback Machine - Maze5.net.
- ↑ Перейти обратно: Перейти обратно: а б с д Виберг, Э.; Холлеман, А.Ф. (2001). Неорганическая химия . Академическая пресса. ISBN 978-0-12-352651-9 .
- ^ Вульфсберг, Гэри (2000). Неорганическая химия . Университетские научные книги. п. 107. ИСБН 9781891389016 .
- ^ Пауэр, Филип П. (сентябрь 2003 г.). «Кремниевые, германиевые, оловянные и свинцовые аналоги ацетиленов». хим. Коммун. (17): 2091–2101. дои : 10.1039/B212224C . ПМИД 13678155 .
- ^ Нагасе, Сигэру; Кобаяши, Каору; Такаги, Нозоми (6 октября 2000 г.). «Тройные связи между более тяжелыми элементами 14 группы. Теоретический подход». Дж. Органомет. хим. 11 (1–2): 264–271. дои : 10.1016/S0022-328X(00)00489-7 .
- ^ Секигути, Акира; Киндзё, Рей; Ичинохе, Масааки (сентябрь 2004 г.). «Стабильное соединение, содержащее тройную связь кремний-кремний» (PDF) . Наука . 305 (5691): 1755–1757. Бибкод : 2004Sci...305.1755S . дои : 10.1126/science.1102209 . ПМИД 15375262 . S2CID 24416825 . [ постоянная мертвая ссылка ]
- ^ Беллерт, Д.; Брекенридж, Вашингтон (2001). «Спектроскопическое определение длины связи молекулы LiOLi: сильная ионная связь». Дж. Хим. Физ. 114 (7): 2871. Бибкод : 2001JChPh.114.2871B . дои : 10.1063/1.1349424 .
- ↑ Перейти обратно: Перейти обратно: а б с д и Гиллеспи, Р.Дж.; Робинсон, Э.А. (2005). «Модели молекулярной геометрии». хим. Соц. Откр. 34 (5): 396–407. дои : 10.1039/b405359c . ПМИД 15852152 .
- ^ Берфорд, Нил; Филлипс, Эндрю; Шурко, Роберт; Василишен, Родерик; Ричардсон, Джон (1997). «Выделение и комплексная характеристика твердого состояния Cl 3 Al–O–PCl 3 » . Химические коммуникации . 1997 (24): 2363–2364 . Проверено 3 апреля 2024 г.
- ^ Уэллс, А. Ф. (1984). Структурная неорганическая химия (5-е изд.). Оксфордские научные публикации. ISBN 978-0-19-855370-0 .
- ^ Петерсон, В.; Холлоуэй, Х.; Койл, А.; Уильямс, М. (сентябрь 1971 г.). «Антипризматическая координация ксенона: структура октафтороксената нитрозония (VI)». Наука . 173 (4003): 1238–1239. Бибкод : 1971Sci...173.1238P . дои : 10.1126/science.173.4003.1238 . ISSN 0036-8075 . ПМИД 17775218 . S2CID 22384146 .
- ^ Хэнсон, Роберт М. (1995). Молекулярное оригами: точные масштабные модели из бумаги . Университетские научные книги. ISBN 978-0-935702-30-9 .
- ↑ Перейти обратно: Перейти обратно: а б Каупп, Мартин (2001). « Не-ВСЕПР» Структуры и связи в d 0 Systems» (PDF) . Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi : 10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO; 2- # ПМИД 11592184 .
- ^ Гиллеспи, Рональд Дж.; Нури, Стефан; Пильме, Жюльен; Сильви, Бернар (2004). «Исследование геометрии d с помощью функции локализации электрона». 0 Молекулы металлов периода 4 от Ca до Mn». Inorg. Chem. 43 (10): 3248–3256. doi : 10.1021/ic0354015 . PMID 15132634 .
- ^ Лэндис, ЧР; Кливленд, Т.; Фирман, ТК (1995). «Понимание формы простых гидридов металлов». Дж. Ам. хим. Соц. 117 (6): 1859–1860. дои : 10.1021/ja00111a036 .
- ^ Лэндис, ЧР; Кливленд, Т.; Фирман, ТК (1996). «Структура W(CH 3 ) 6 » . Наука . 272 (5259): 179–183. дои : 10.1126/science.272.5259.179f .
- ^ Чжай, HJ; Ли, С.; Диксон, Д.А.; Ван, Л.С. (2008). «Исследование электронных и структурных свойств кластеров оксида хрома (CrO
3 ) −
n и (CrO 3 ) n ( n = 1–5): Фотоэлектронная спектроскопия и расчеты функциональной плотности». Журнал Американского химического общества . 130 (15): 5167–77. doi : 10.1021/ja077984d . PMID 18327905 . - ^ Кинг, Р. Брюс (2000). «Атомные орбитали, симметрия и координационные многогранники». Коорд. хим. Преподобный . 197 : 141–168. дои : 10.1016/s0010-8545(99)00226-x .
- ^ Хаалан, А.; Хаммель, А.; Ридпал, К.; Волден, Х.В. (1990). «Координационная геометрия газообразного гексаметилвольфрама не октаэдрическая». Дж. Ам. хим. Соц. 112 (11): 4547–4549. дои : 10.1021/ja00167a065 .
- ^ Гринвуд, Норман Н .; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-08-037941-8 .
- ^ Сейхо, Луис; Барандьяран, Зойла; Хузинага, Сигеру (1991). «Потенциальное изучение равновесной геометрии дигалогенидов щелочноземельных металлов с помощью модели ab initio: MX 2 (M = Mg, Ca, Sr, Ba; X = F, Cl, Br, I)» (PDF) . Дж. Хим. Физ. 94 (5): 3762. Бибкод : 1991ЖЧФ..94.3762С . дои : 10.1063/1.459748 . hdl : 10486/7315 .
- ^ Сет, Майкл; Швердтфегер, Питер; Фегри, Кнут (1999). «Химия сверхтяжелых элементов. III. Теоретические исследования соединений 113-го элемента» . Журнал химической физики . 111 (14): 6422–6433. Бибкод : 1999JChPh.111.6422S . дои : 10.1063/1.480168 . S2CID 41854842 .
- ^ Бэ, Ч.; Хан, Ю.-К.; Ли, йо. С. (18 января 2003 г.). «Спин-орбитальные и релятивистские эффекты на структуры и стабильность фторидов группы 17 EF 3 (E = I, At и элемент 117): индуцированная относительностью стабильность структуры D 3h (117) F 3 ». Журнал физической химии А. 107 (6): 852–858. Бибкод : 2003JPCA..107..852B . дои : 10.1021/jp026531m .
- ^ Хан, Ён-Кю; Ли, Юн Соп (1999). «Структуры RgFn (Rg = Xe, Rn и элемент 118. n = 2, 4.), рассчитанные двухкомпонентными спин-орбитальными методами. Изомер (118)F 4 , индуцированный спин-орбитой ». Журнал физической химии А. 103 (8): 1104–1108. Бибкод : 1999JPCA..103.1104H . дои : 10.1021/jp983665k .
- ^ Анслин, Э.В.; Догерти, Д.А. (2006). Современная физико-органическая химия . Университетские научные книги. п. 57. ИСБН 978-1891389313 .
Дальнейшее чтение [ править ]
- Лаговский, Дж. Дж., изд. (2004). Химия: основы и приложения . Том. 3. Нью-Йорк: Макмиллан. стр. 99–104 . ISBN 978-0-02-865721-9 .
Внешние ссылки [ править ]
- VSEPR AR — 3D-визуализация теории VSEPR с помощью приложения дополненной реальности
- 3D Chem — химия, структуры и трехмерные молекулы.
- Центр молекулярной структуры Университета Индианы (IUMSC)