Теория молекулярных орбиталей
В химии теория молекулярных орбиталей (теория МО или МОТ) — это метод описания электронной структуры молекул с помощью квантовой механики . Это было предложено в начале 20 века.
В теории молекулярных орбиталей электроны в молекуле не относят к отдельным химическим связям между атомами , а рассматриваются как движущиеся под воздействием атомных ядер во всей молекуле. [1] Квантовая механика описывает пространственные и энергетические свойства электронов как молекулярных орбиталей, которые окружают два или более атомов в молекуле и содержат валентные электроны между атомами.
Теория молекулярных орбиталей произвела революцию в изучении химической связи, аппроксимировав состояния связанных электронов — молекулярных орбиталей — как линейные комбинации атомных орбиталей (ЛКАО). Эти аппроксимации выполняются путем применения теории функционала плотности (DFT) или моделей Хартри – Фока (HF) к уравнению Шредингера .
Теория молекулярных орбиталей и теория валентных связей являются основополагающими теориями квантовой химии .
комбинации атомных орбиталей ( Метод линейной ЛКАО )
В методе ЛКАО каждая молекула имеет набор молекулярных орбиталей . Предполагается, что волновая функция молекулярной орбитали ψ j может быть записана как простая взвешенная сумма n составляющих атомных орбиталей χ i в соответствии со следующим уравнением: [2]
определить можно Коэффициенты cij численно, подставив это уравнение в уравнение Шредингера и применив вариационный принцип . Вариационный принцип — это математический метод, используемый в квантовой механике для построения коэффициентов базиса каждой атомной орбиты. Больший коэффициент означает, что базис орбитали в большей степени состоит из этой конкретной атомной орбитали - следовательно, молекулярная орбиталь лучше всего характеризуется этим типом. Этот метод количественной оценки вклада орбиталей как линейной комбинации атомных орбиталей используется в вычислительной химии . К системе можно применить дополнительное унитарное преобразование для ускорения сходимости в некоторых вычислительных схемах. Теория молекулярных орбиталей рассматривалась как конкурент теории валентных связей в 1930-х годах, прежде чем стало понятно, что эти два метода тесно связаны и что при расширении они становятся эквивалентными.
Теория молекулярных орбиталей используется для интерпретации ультрафиолетовой-видимой спектроскопии (УФ-ВИД). Изменения электронной структуры молекул можно увидеть по поглощению света определенных длин волн. Этим сигналам можно приписать переход электронов, движущихся с одной орбитали с более низкой энергией на орбиталь с более высокой энергией. Диаграмма молекулярных орбиталей конечного состояния описывает электронную природу молекулы в возбужденном состоянии.
Существует три основных требования к комбинациям атомных орбиталей, которые могут быть пригодны в качестве приближенных молекулярных орбиталей.
- Комбинация атомных орбиталей должна иметь правильную симметрию, а это означает, что она должна принадлежать правильному неприводимому представлению группы симметрии молекулы . Используя адаптированные к симметрии линейные комбинации , или SALC, можно сформировать молекулярные орбитали правильной симметрии.
- Атомные орбитали также должны перекрываться в космосе. Они не могут объединиться в молекулярные орбитали, если находятся слишком далеко друг от друга.
- Атомные орбитали должны находиться на одинаковых энергетических уровнях, чтобы объединиться в молекулярные орбитали. Потому что если разница в энергии велика, то при формировании молекулярных орбиталей изменение энергии становится небольшим. Следовательно, уменьшение энергии электронов недостаточно для образования значительной связи. [3]
История [ править ]
Теория молекулярных орбиталей была разработана через несколько лет после теории валентных связей создания (1927 г.), главным образом благодаря усилиям Фридриха Хунда , Роберта Малликена , Джона К. Слейтера и Джона Леннарда-Джонса . [4] Теория МО первоначально называлась теорией Хунда-Малликена. [5] По словам физика и физико-химика Эриха Хюкеля , первым количественным применением теории молекулярных орбиталей была статья Леннарда-Джонса 1929 года . [6] [7] В этой статье было предсказано триплетное основное состояние молекулы дикислорода , что объяснило ее парамагнетизм. [8] (см. Молекулярную орбитальную диаграмму § Диоксид кислорода ) до теории валентных связей, которая в 1931 году предложила собственное объяснение. [9] Слово орбиталь было введено Малликеном в 1932 году. [5] К 1933 году теория молекулярных орбиталей была признана действительной и полезной теорией. [10]
Эрих Хюкель применил теорию молекулярных орбиталей к молекулам ненасыщенных углеводородов, начиная с 1931 года с помощью своего метода молекулярных орбиталей Хюкеля (HMO) для определения энергии МО для пи-электронов , который он применил к сопряженным и ароматическим углеводородам. [11] [12] Этот метод позволил объяснить стабильность молекул с шестью пи-электронами, таких как бензол .
Первый точный расчет молекулярной орбитальной волновой функции был сделан Чарльзом Коулсоном в 1938 году на молекуле водорода. [13] К 1950 году молекулярные орбитали были полностью определены как собственные функции самосогласованного поля (волновые функции) гамильтониана , и именно в этот момент теория молекулярных орбиталей стала полностью строгой и последовательной. [14] Этот строгий подход известен как метод Хартри-Фока для молекул, хотя он берет свое начало в расчетах на атомах. В расчетах на молекулах молекулярные орбитали расширяются с точки зрения базисного набора атомных орбиталей , что приводит к уравнениям Рутана . [15] Это привело к развитию многих ab initio методов квантовой химии . Параллельно теория молекулярных орбиталей применялась более приближенным образом с использованием некоторых эмпирически полученных параметров в методах, теперь известных как полуэмпирические методы квантовой химии . [15]
Успех теории молекулярных орбиталей также породил теорию поля лигандов , которая была разработана в 1930-х и 1940-х годах как альтернатива теории кристаллического поля .
Типы орбиталей [ править ]
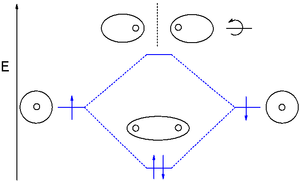
Теория молекулярных орбиталей (МО) использует линейную комбинацию атомных орбиталей (ЛКАО) для представления молекулярных орбиталей, возникающих в результате связей между атомами. Их часто делят на три типа: связывающие , разрыхляющие и несвязывающие . Связующая орбиталь концентрирует электронную плотность в области между данной парой атомов, так что ее электронная плотность будет стремиться притягивать каждое из двух ядер к другому и удерживать два атома вместе. [16] Разрыхляющая орбиталь концентрирует электронную плотность «за» каждым ядром (т. е. на стороне каждого атома, которая находится дальше всего от другого атома), и поэтому имеет тенденцию оттягивать каждое из двух ядер от другого и фактически ослаблять связь между ними. два ядра. Электроны на несвязывающих орбиталях, как правило, связаны с атомными орбиталями, которые не взаимодействуют друг с другом ни положительно, ни отрицательно, а электроны на этих орбиталях не способствуют укреплению связи и не уменьшают ее. [16]
Молекулярные орбитали подразделяются в зависимости от типов атомных орбиталей, из которых они образованы. Химические вещества будут образовывать связывающие взаимодействия, если их орбитали уменьшают энергию при взаимодействии друг с другом. Выделяют разные связывающие орбитали, различающиеся электронной конфигурацией (формой электронного облака) и энергетическими уровнями .
Молекулярные орбитали молекулы можно проиллюстрировать диаграммами молекулярных орбиталей .
Обычными связывающими орбиталями являются сигма (σ) орбитали , симметричные относительно оси связи, и пи (π) орбитали с узловой плоскостью вдоль оси связи. Реже встречаются дельта-(δ)-орбитали и фи-(φ)-орбитали с двумя и тремя узловыми плоскостями соответственно вдоль оси связи. Разрыхляющие орбитали отмечены звездочкой. Например, разрыхляющая пи-орбиталь может быть обозначена как π*.
Ордер на залог [ править ]

Порядок связи — это количество химических связей между парой атомов. Порядок связи молекулы можно рассчитать, вычитая количество электронов на разрыхляющих орбиталях из числа связывающих орбиталей, а затем полученное число делят на два. Ожидается, что молекула стабильна, если ее порядок связи больше нуля. достаточно рассмотреть валентный электрон Для определения порядка связи . Потому что (для главного квантового числа n>1), когда МО происходят из 1s АО, разница в количестве электронов на связывающей и разрыхляющей молекулярной орбитали равна нулю. Таким образом, нет никакого общего влияния на порядок связи, если электрон не является валентным.
Порядок связи = 1/2 [(Количество электронов в связывающей МО) - (Количество электронов в разрыхляющей МО)]
Зная порядок связи, можно предсказать, образуется связь между двумя атомами или нет. Например, существование молекулы He 2 . Из диаграммы молекулярных орбиталей порядок связи = 1/2 * (2-2) = 0. Это означает, что между двумя атомами He не произойдет образования связи, что и наблюдается экспериментально. Его можно обнаружить при очень низкой температуре и давлении молекулярного луча, и он имеет энергию связи примерно 0,001 Дж/моль. [17]
Кроме того, прочность связи также может быть оценена по порядку связи (BO). Например:
Н 2 :BO=(2-0)/2=1; Энергия связи = 436 кДж/моль.
Ч 2 + :BO=(1-0)/2=1/2; Энергия связи=171 кДж/моль.
По порядку связи H 2 + меньше, чем H 2 , он должен быть менее стабильным, что наблюдается экспериментально и видно по энергии связи.
Обзор [ править ]
Этот раздел нуждается в дополнительных цитатах для проверки . ( сентябрь 2020 г. ) |
MOT обеспечивает глобальный, делокализованный взгляд на химическую связь . В теории МО любой электрон в молекуле может находиться где угодно в молекуле, поскольку квантовые условия позволяют электронам перемещаться под влиянием сколь угодно большого числа ядер, пока они находятся в собственных состояниях, разрешенных определенными квантовыми правилами. Таким образом, при возбуждении необходимым количеством энергии высокочастотным светом или другими способами электроны могут перейти на молекулярные орбитали с более высокой энергией. Например, в простом случае двухатомной молекулы водорода продвижение одного электрона со связывающей орбитали на разрыхляющую орбиталь может происходить под действием УФ-излучения. Это продвижение ослабляет связь между двумя атомами водорода и может привести к фотодиссоциации — разрыву химической связи из-за поглощения света.
Теория молекулярных орбиталей используется для интерпретации ультрафиолетовой-видимой спектроскопии (УФ-ВИД). Изменения электронной структуры молекул можно увидеть по поглощению света определенных длин волн. Этим сигналам можно приписать переход электронов, движущихся с одной орбитали с более низкой энергией на орбиталь с более высокой энергией. Диаграмма молекулярных орбиталей конечного состояния описывает электронную природу молекулы в возбужденном состоянии.
Хотя в теории МО некоторые молекулярные орбитали могут содержать электроны, более локализованные между определенными парами молекулярных атомов, другие орбитали могут содержать электроны, которые более равномерно распределены по молекуле. Таким образом, в целом связь в теории МО гораздо более делокализована, что делает ее более применимой к резонансным молекулам, которые имеют эквивалентные нецелые порядки связей, чем теория валентных связей . Это делает теорию МО более полезной для описания расширенных систем.
Роберт С. Малликен , активно участвовавший в появлении теории молекулярных орбиталей, считает каждую молекулу самодостаточной единицей. Он утверждает в своей статье:
...Попытки рассматривать молекулу как состоящую из определенных атомных или ионных единиц, удерживаемых вместе дискретным числом связывающих электронов или электронных пар, считаются более или менее бессмысленными, за исключением приближения в особых случаях или метода расчета. […]. Молекула здесь рассматривается как совокупность ядер, вокруг каждого из которых группируется электронная конфигурация, очень подобная конфигурации свободного атома во внешнем поле, за исключением того, что внешние части электронных конфигураций, окружающие каждое ядро, обычно принадлежат, частично, , совместно с двумя или более ядрами.... [18]
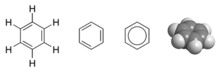
Примером может служить МО-описание бензола , C
66Ч
6 , представляющее собой ароматическое гексагональное кольцо из шести атомов углерода и трех двойных связей. В этой молекуле 24 из 30 общих валентных связывающих электронов - 24 исходящих от атомов углерода и 6 - от атомов водорода - расположены на 12 σ (сигма) связывающих орбиталях, которые расположены в основном между парами атомов (CC или CH). аналогично электронам в описании валентной связи. Однако в бензоле оставшиеся шесть связывающих электронов расположены на трех π (pi) молекулярных связующих орбиталях, которые делокализованы вокруг кольца. Два из этих электронов находятся в МО, которая имеет равные орбитальные вклады от всех шести атомов. Остальные четыре электрона находятся на орбиталях с вертикальными узлами, расположенными под прямым углом друг к другу. Как и в теории ВБ, все эти шесть делокализованных π-электронов находятся в большем пространстве, которое существует выше и ниже плоскости кольца. Все углерод-углеродные связи в бензоле химически эквивалентны. В теории МО это является прямым следствием того факта, что три молекулярные π-орбитали объединяются и равномерно распределяют дополнительные шесть электронов по шести атомам углерода.
В таких молекулах, как метан , CH
4 , восемь валентных электронов находятся в четырех МО, которые распределены по всем пяти атомам. Возможно преобразование МО в четыре локализованных sp 3 орбитали. Лайнус Полинг в 1931 году гибридизовал 2s- и 2p-орбитали углерода так, что они указывали непосредственно на базисные функции 1s водорода и имели максимальное перекрытие. Однако делокализованное описание МО более подходит для прогнозирования энергий ионизации и положения спектральных полос поглощения . Когда метан ионизируется, один электрон отрывается от валентных МО, которые могут исходить от уровней s-связи или трижды вырожденных уровней p-связи, что дает две энергии ионизации. Для сравнения, объяснение в теории валентных связей более сложное. Когда один электрон удаляется из sp 3 орбитальный резонанс возникает между четырьмя структурами валентных связей, каждая из которых имеет одну одноэлектронную связь и три двухэлектронные связи. Трижды вырожденные Т 2 и А 1 ионизированные состояния (CH 4 + ) производятся из различных линейных комбинаций этих четырех структур. Разница в энергии между ионизированным и основным состоянием дает две энергии ионизации.
Как и в бензоле, в таких веществах, как бета-каротин , хлорофилл или гем , некоторые электроны на π-орбиталях распределяются по молекулярным орбиталям на большие расстояния в молекуле, что приводит к поглощению света при более низких энергиях ( видимый спектр ), что объясняет для характерных цветов этих веществ. [19] Эти и другие спектроскопические данные для молекул хорошо объясняются в теории МО с упором на электронные состояния, связанные с многоцентровыми орбиталями, включая смешивание орбиталей, основанное на принципах согласования орбитальной симметрии. [16] Те же принципы МО естественным образом объясняют некоторые электрические явления, такие как высокая электропроводность в плоском направлении гексагональных атомных листов, существующих в графите . Это является результатом непрерывного перекрытия зон наполовину заполненных p-орбиталей и объясняет электропроводность. Теория МО признает, что некоторые электроны в атомных листах графита полностью делокализованы на произвольных расстояниях и находятся на очень больших молекулярных орбиталях, которые покрывают весь лист графита, и поэтому некоторые электроны могут свободно перемещаться и, следовательно, проводить электричество в плоскости листа. как будто они находились в металле.
См. также [ править ]
Ссылки [ править ]
- ^ Дэйнтит, Дж. (2004). Оксфордский химический словарь . Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-860918-6 .
- ^ Ликер, Марк, Дж. (2004). Краткая химическая энциклопедия МакГроу-Хилла . Нью-Йорк: МакГроу-Хилл. ISBN 978-0-07-143953-4 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Мисслер, Гэри Л.; Фишер, Пол Дж.; Тарр, Дональд А. (8 апреля 2013 г.). Неорганическая химия . Пирсон Образование. ISBN 978-0-321-91779-9 .
- ^ Коулсон, Чарльз, А. (1952). Валентность . Оксфорд в Clarendon Press.
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ↑ Перейти обратно: Перейти обратно: а б Малликен, Роберт С. (1972) [1966]. «Спектроскопия, молекулярные орбитали и химическая связь» (PDF) (пресс-релиз). Нобелевские лекции по химии 1963–1970 гг. Амстердам: Издательская компания Elsevier.
- ^ Хюкель, Эрих (1934). «Теория свободных радикалов органической химии». Пер. Фарадей Соц . 30 : 40–52. дои : 10.1039/TF9343000040 .
- ^ Леннард-Джонс, Дж. Э. (1929). «Электронное строение некоторых двухатомных молекул». Пер. Фарадей Соц . 25 : 668–686. Бибкод : 1929ФаТр...25..668Л . дои : 10.1039/TF9292500668 .
- ^ Коулсон, Калифорния Валенс (2-е изд., Oxford University Press, 1961), стр.103
- ^ Полинг, Лайнус (1931). «Природа химической связи. II. Одноэлектронная связь и трехэлектронная связь». Дж. Ам. хим. Соц . 53 (9): 3225–3237. дои : 10.1021/ja01360a004 .
- ^ Холл, Джордж Г. (1991). «Документ Леннарда-Джонса 1929 года и основы теории молекулярных орбиталей» . Достижения квантовой химии . 22 : 1–6. Бибкод : 1991AdQC...22....1H . дои : 10.1016/S0065-3276(08)60361-5 . ISBN 978-0-12-034822-0 . ISSN 0065-3276 .
- ^ Э. Хюкель, Журнал физики , 70 , 204 (1931); 72 , 310 (1931); 76 , 628 (1932); 83 , 632 (1933).
- ^ Теория Хюкеля для химиков-органиков , К. А. Коулсон , Б. О'Лири и Р.Б. Маллион, Academic Press, 1978.
- ^ Коулсон, Калифорния (1938), «Самосогласованное поле для молекулярного водорода», Mathematical Proceedings of the Cambridge Philosophical Society , 34 (2): 204–212, Bibcode : 1938PCPS...34..204C , doi : 10.1017/S0305004100020089 , S2CID 95772081
- ^ Холл, Г.Г. (7 августа 1950 г.). «Молекулярно-орбитальная теория химической валентности. VI. Свойства эквивалентных орбиталей». Учеб. Р. Сок. А. 202 (1070): 336–344. Бибкод : 1950RSPSA.202..336H . дои : 10.1098/rspa.1950.0104 . S2CID 123260646 .
- ↑ Перейти обратно: Перейти обратно: а б Дженсен, Фрэнк (1999). Введение в вычислительную химию . Джон Уайли и сыновья. ISBN 978-0-471-98425-2 .
- ↑ Перейти обратно: Перейти обратно: а б с Мисслер и Тарр (2013), Неорганическая химия , 5-е изд., 117–165, 475–534.
- ^ Мисслер, Гэри Л.; Фишер, Пол Дж.; Тарр, Дональд А. (8 апреля 2013 г.). Неорганическая химия . Пирсон Образование. ISBN 978-0-321-91779-9 .
- ^ Малликен, Р.С. (октябрь 1955 г.). «Электронный популяционный анализ молекулярных волновых функций ЛКАО – МО. I» . Журнал химической физики . 23 (10): 1833–1840. Бибкод : 1955ЖЧФ..23.1833М . дои : 10.1063/1.1740588 . ISSN 0021-9606 .
- ^ Гриффит, Дж. С. и Л. Е. Оргель. «Теория лигандного поля». Q. Преподобный Chem. Соц. 1957, 11, 381–383.
Внешние ссылки [ править ]
- Теория молекулярных орбиталей - Университет Пердью
- Теория молекулярных орбиталей — Спаркноты
- Теория молекулярных орбиталей - Химический сайт Марка Бишопа
- Введение в теорию МО - Королева Мэри, Лондонский университет
- Теория молекулярных орбиталей - таблица связанных терминов
- Введение в теорию молекулярных групп - Оксфордский университет
