Теория поля лигандов
Теория поля лигандов ( LFT ) описывает связь, расположение орбиталей и другие характеристики координационных комплексов . [1] [2] [3] [4] Он представляет собой применение теории молекулярных орбиталей к переходных металлов комплексам . Ион переходного металла имеет девять валентных атомных орбиталей , состоящих из пяти n d, одной ( n +1) и трех ( n + 1) p-орбиталей. Эти орбитали обладают соответствующей энергией для образования связывающих взаимодействий с лигандами . LFT-анализ сильно зависит от геометрии комплекса, но большинство объяснений начинаются с описания октаэдрических комплексов, где шесть лигандов координируются с металлом. Другие комплексы можно описать со ссылкой на теорию кристаллического поля . [5] Теория поля инвертированных лигандов (ILFT) развивает LFT, разрушая предположения, сделанные об относительных энергиях орбиталей металлов и лигандов.
История [ править ]
Теория поля лигандов возникла в результате объединения принципов, заложенных в теории молекулярных орбиталей и теории кристаллического поля , которые описывают потерю вырождения d-орбиталей металлов в комплексах переходных металлов. Джон Стэнли Гриффит и Лесли Оргел [6] отстаивал теорию поля лигандов как более точное описание таких комплексов, хотя эта теория возникла в 1930-х годах с работами по магнетизму Джона Хасбрука Ван Флека . Гриффит и Оргель использовали электростатические принципы, установленные в теории кристаллического поля, для описания ионов переходных металлов в растворе и использовали теорию молекулярных орбиталей для объяснения различий во взаимодействиях металл-лиганд, тем самым объясняя такие наблюдения, как стабилизация кристаллического поля и видимые спектры комплексов переходных металлов. В своей статье они предположили, что основной причиной различий в цвете комплексов переходных металлов в растворе являются неполные подоболочки d-орбитали. [6] То есть в связывании участвуют незанятые d-орбитали переходных металлов, что влияет на цвета, которые они поглощают в растворе. В теории поля лигандов на различные d-орбитали воздействуют по-разному, когда они окружены полем соседних лигандов, и их энергия повышается или понижается в зависимости от силы их взаимодействия с лигандами. [6]
Связывание [ править ]
σ-связь (сигма-связь) [ править ]
созданные в результате координации, можно рассматривать как результат отдачи двух электронов каждым из шести σ-донорных лигандов d - орбиталям металла В октаэдрическом комплексе молекулярные орбитали , . В октаэдрических комплексах лиганды сближаются по осям x- , y- и z , поэтому их орбитали σ-симметрии образуют связывающие и разрыхляющие комбинации с d z 2 и d х 2 − и 2 орбитали. Орбитали d xy , d xz и d yz остаются несвязывающими орбиталями. Также происходят некоторые слабые связывающие (и разрыхляющие) взаимодействия с s- и p -орбиталями металла, в результате чего в общей сложности образуется 6 связывающих (и 6 разрыхляющих) молекулярных орбиталей. [7]
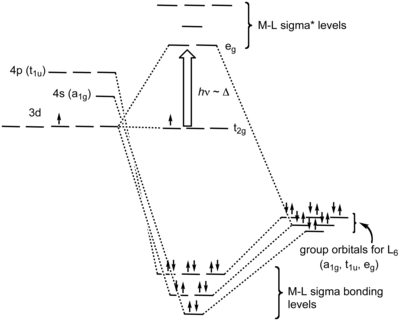
С точки зрения молекулярной симметрии , шесть неподеленных пар орбиталей лигандов (по одной от каждого лиганда) образуют шесть адаптированных к симметрии линейных комбинаций (SALC) орбиталей, также иногда называемых орбиталями группы лигандов (LGO). Неприводимые представления пролеты суть a 1g , t 1u и eg о том, что эти . У металла также есть шесть валентных орбиталей, которые охватывают эти представления : s-орбиталь обозначена 1g неприводимые , набор из трех p-орбиталей обозначен t 1u , а d z 2 и d х 2 − и 2 орбитали обозначены, например , . Шесть σ-связывающих молекулярных орбиталей возникают в результате комбинации лигандных SALC с металлическими орбиталями той же симметрии. [8]
π-связь (пи-связь) [ править ]
π-связь в октаэдрических комплексах происходит двумя способами: через любые p -орбитали лиганда, не участвующие в σ-связывании, и через любые π или π * молекулярные орбитали, присутствующие на лиганде.
В обычном анализе p -орбитали металла используются для σ-связывания (и имеют неправильную симметрию , чтобы перекрываться с лигандом p, π или π). * в любом случае орбитали), поэтому π-взаимодействия происходят с соответствующими металлическими d -орбиталями, то есть d xy , d xz и d yz . Это орбитали, которые не являются несвязывающими, когда имеет место только σ-связь.
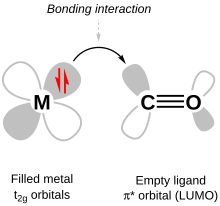
Одной из важных π-связей в координационных комплексах является π-связь металла с лигандом, также называемая π-связью . Это происходит, когда LUMO (самые низкие незанятые молекулярные орбитали) лиганда разрыхляют связь π. * орбитали. Эти орбитали близки по энергии к орбиталям dxy , с которыми , dxz они объединяются , и dyz образуя связывающие орбитали (т.е. орбитали с более низкой энергией, чем вышеупомянутый набор d -орбиталей). Соответствующие разрыхляющие орбитали имеют более высокую энергию, чем разрыхляющие орбитали от σ-связи, поэтому после того, как новые π-связывающие орбитали заполняются электронами от d -орбиталей металла, Δ O увеличивается и связь между лигандом и металл укрепляется. Лиганды оказываются с электронами в своих π * молекулярная орбиталь, поэтому соответствующая π-связь внутри лиганда ослабляется.
Другой формой координационной π-связи является связь лиганд-металл. или π-орбиталей π-симметрии Такая ситуация возникает при заполнении p- лигандов. Они объединяются с орбиталями d xy , d xz и d yz на металле и отдают электроны образовавшейся орбитали связи π-симметрии между ними и металлом. Связь металл-лиганд несколько усиливается в результате этого взаимодействия, но дополнительная разрыхляющая молекулярная орбиталь от связи лиганд-металл не выше по энергии, чем разрыхляющая молекулярная орбиталь от σ-связи. Однако он заполняется электронами с d -орбиталей металла, становясь, однако, ВЗМО (высшей занятой молекулярной орбиталью) комплекса. По этой причине Δ O уменьшается, когда происходит связь лиганда с металлом.
Большая стабилизация, возникающая в результате связывания металла с лигандом, вызвана передачей отрицательного заряда от иона металла к лигандам. Это позволяет металлу легче воспринимать σ-связи. Сочетание σ-связи лиганд-металл и металл-лиганд.π-связь представляет собой синергический эффект, поскольку одно усиливает другое.
Поскольку каждый из шести лигандов имеет две орбитали π-симметрии, всего их двенадцать. Их линейные комбинации, адаптированные к симметрии, распадаются на четыре трижды вырожденных неприводимых представления, одно из которых имеет t2g симметрию . Орбитали d xy , d xz и d yz на металле также обладают этой симметрией, и поэтому π-связи, образующиеся между центральным металлом и шестью лигандами, также имеют ее (поскольку эти π-связи просто образуются в результате перекрытия двух наборов орбиталей с симметрией t 2g .)
и низкий спин и спектрохимический Высокий ряд
Образующиеся шесть связывающих молекулярных орбиталей «наполняются» электронами от лигандов, а электроны с d -орбиталей иона металла занимают несвязывающие, а в некоторых случаях и разрыхляющие МО. Разность энергий между двумя последними типами МО называется Δ O (O означает октаэдрический) и определяется характером π-взаимодействия орбиталей лиганда с d -орбиталями центрального атома. Как описано выше, π-донорные лиганды приводят к малому Δ O и называются лигандами слабого или низкого поля, тогда как π-акцепторные лиганды приводят к большому значению Δ O и называются лигандами сильного или сильного поля. Лиганды, которые не являются ни π-донором, ни π-акцептором, дают значение Δ O где-то посередине.
Размер Δ O определяет электронную структуру d 4 - д 7 ионы. В комплексах металлов с этими d -электронными конфигурациями несвязывающие и разрыхляющие молекулярные орбитали могут заполняться двумя способами: один, при котором как можно больше электронов помещается на несвязывающие орбитали перед заполнением разрыхляющих орбиталей. орбитали, и тот, в который помещено как можно больше неспаренных электронов. Первый случай называется низкоспиновым, а второй - высокоспиновым. Небольшое Δ O можно преодолеть за счет энергетического выигрыша от отсутствия спаривания электронов, что приводит к образованию высокого спина. Однако когда Δ O велико, энергия спинового спаривания становится незначительной по сравнению с этим и возникает низкоспиновое состояние.
Спектрохимический ряд представляет собой полученный эмпирическим путем список лигандов, упорядоченный по размеру расщепления Δ, которое они производят. Видно, что все слабополевые лиганды являются π-донорами (например, I − ), лиганды сильного поля являются π-акцепторами (такими как CN − и CO), а лиганды, такие как H 2 O и NH 3 , которые не являются ни тем, ни другим, находятся посередине.
я − < Бр − < С 2− < СКН − <Кл − < НЕТ 3 − < Н 3 − < Ф − < ОН − < С 2 О 4 2− < H 2 O < NCS − < CH 3 CN < py ( пиридин ) < NH 3 < en ( этилендиамин ) < bipy ( 2,2'-бипиридин ) < phen (1,10- фенантролин ) < NO 2 − < ПФ 3 < CN − < СО
См. также [ править ]
- Теория кристаллического поля
- Лиганд-зависимый путь
- Теория молекулярных орбиталей
- Нефелауксетический эффект
Ссылки [ править ]
- ^ Боллхаузен, Карл Йохан, «Введение в теорию поля лигандов», McGraw-Hill Book Co., Нью-Йорк, 1962 г.
- ^ Гриффит, Дж. С. (2009). Теория ионов переходных металлов (переиздание). Издательство Кембриджского университета. ISBN 978-0521115995 .
- ^ Шлефер, Х.Л.; Глиманн, Г. «Основные принципы теории поля лигандов» Wiley Interscience: Нью-Йорк; 1969 год
- ^ Бхатт, Васишта (01 января 2016 г.), Бхатт, Васишта (редактор), «Глава 1 - Основная координационная химия» , Основы координационной химии , Academic Press, стр. 1–35, doi : 10.1016/b978-0- 12-803895-6.00001-х , ISBN 978-0-12-803895-6 , получено 18 июня 2024 г.
- ^ Г. Л. Мисслер и Д. А. Тарр «Неорганическая химия», 3-е изд., Пирсон / Прентис Холл, ISBN 0-13-035471-6 .
- ^ Jump up to: Перейти обратно: а б с Гриффит, Дж. С. и Л. Е. Оргель. «Теория лигандного поля». Q. Преподобный Chem. Соц. 1957, 11, 381–393.
- ^ «10.3.1: Теория поля лигандов — молекулярные орбитали октаэдрического комплекса» . Химия LibreTexts . 03.09.2021 . Проверено 7 декабря 2023 г.
- ^ «10.3.1: Теория поля лигандов — молекулярные орбитали октаэдрического комплекса» . Химия LibreTexts . 03.09.2021 . Проверено 7 декабря 2023 г.
Внешние ссылки [ править ]
- Теория кристаллического поля, метод сильной связи и эффект Яна-Теллера в книге Э. Паварини, Э. Коха, Ф. Андерса и М. Джаррелла (ред.): Коррелированные электроны: от моделей к материалам, Юлих, 2012 г., ISBN 978-3-89336-796-2