Октаэдрическая молекулярная геометрия

Октаэдрическая молекулярная геометрия
Октаэдрическая молекулярная геометрия
Примеры	SF 6 , Мо(СО) 6
Группа точек	Ой
Координационный номер	6
Угол(а) связи	90°
μ (полярность)	0

В химии октаэдрическая молекулярная геометрия , также называемая квадратной бипирамидальной , ^[1] описывает форму соединений с шестью атомами или группами атомов или лигандов, симметрично расположенных вокруг центрального атома, определяющих вершины октаэдра . Октаэдр имеет восемь граней, отсюда и приставка окта . Октаэдр — одно из платоновых тел , хотя октаэдрические молекулы обычно имеют атом в центре и не имеют связей между атомами-лигандами. Совершенный октаэдр принадлежит группе Oh _. точечной Примерами октаэдрических соединений являются гексафторид серы SF ₆ и гексакарбонил молибдена Mo(CO) ₆ . Термин «октаэдрический» используется химиками довольно широко, уделяя особое внимание геометрии связей с центральным атомом и не учитывая различия между самими лигандами. Например, [Со(NH ₃ ) ₆ ] ³⁺, который не является октаэдрическим в математическом смысле из-за ориентации Связи N-H называются октаэдрическими. ^[2]

Концепция октаэдрической координационной геометрии была разработана Альфредом Вернером для объяснения стехиометрии и изомерии в координационных соединениях . Его проницательность позволила химикам рационализировать количество изомеров координационных соединений. Октаэдрические комплексы переходных металлов, содержащие амины и простые анионы, часто называют комплексами типа Вернера .

Структура гексафторида серы , примера молекулы с октаэдрической координационной геометрией.

Изомерия в октаэдрических комплексах

Когда два или более типов лигандов (L ^а, Л ^б, ...) координированы с октаэдрическим металлоцентром (М), комплекс может существовать в виде изомеров. Система наименования этих изомеров зависит от количества и расположения различных лигандов.

цис и транс

Для ML ^а
₄ л ^б
₂ , существуют два изомера. Эти изомеры ML ^а
₄ л ^б
₂ являются цис- , если L ^б лиганды взаимно соседствуют, и транс , если L ^б группы расположены под углом 180° друг к другу. Именно анализ таких комплексов привел Альфреда Вернера к постулированию октаэдрических комплексов, получившему Нобелевскую премию 1913 года.

цис- [CoCl ₂ (NH ₃ ) ₄ ] ⁺
транс- [CoCl ₂ (NH ₃ ) ₄ ] ⁺

Фациальные и меридиональные изомеры

Для ML ^а
₃ л ^б
₃ , возможны два изомера — фациальный изомер ( fac ), у которого каждый набор из трех одинаковых лигандов занимает одну грань октаэдра, окружающего атом металла, так что любые два из этих трех лигандов являются взаимно цис-изомерами, и меридиональный изомер ( mer ), в котором каждый набор из трёх одинаковых лигандов занимает плоскость, проходящую через атом металла.

fac -[CoCl ₃ (NH ₃ ) ₃ ]
мер -[CoCl ₃ (NH ₃ ) ₃ ]

Δ и Λ-изомеры

Комплексы с тремя бидентатными лигандами или двумя цис- бидентатными лигандами могут существовать в виде энантиомерных пар. Примеры показаны ниже.

Λ- [Fe(ox) ₃ ] ³⁻
Δ -[Fe(ox) ₃ ] ³⁻
Λ - цис- (en)_[CoCl ⁺
Δ - цис - (en)_[CoCl ⁺

Другой

Для ML ^а
₂ л ^б
₂ л ^с
₂ , всего возможны пять геометрических изомеров и шесть стереоизомеров. ^[3]

Один изомер, у которого все три пары идентичных лигандов находятся в транс- положении.
Три изомера, в которых одна пара идентичных лигандов (L ^а или Л ^б или Л ^с) является транс , тогда как две другие пары лигандов взаимно цис .
Две энантиомерные пары, в которых все три пары идентичных лигандов являются цис-цисами . Они эквивалентны упомянутым выше изомерам Δ и Λ.

Число возможных изомеров может достигать 30 для октаэдрического комплекса с шестью различными лигандами (напротив, для тетраэдрического комплекса с четырьмя различными лигандами возможны только два стереоизомера). В следующей таблице перечислены все возможные комбинации монодентатных лигандов:

Формула	Количество изомеров	Количество энантиомерных пар
МЛ ₆	1	0
МЛ ^а ₅ л ^б	1	0
МЛ ^а ₄ л ^б ₂	2	0
МЛ ^а ₄ л ^бл ^с	2	0
МЛ ^а ₃ л ^б ₃	2	0
МЛ ^а ₃ л ^б ₂ л ^с	3	0
МЛ ^а ₃ л ^бл ^сл ^д	5	1
МЛ ^а ₂ л ^б ₂ л ^с ₂	6	1
МЛ ^а ₂ л ^б ₂ л ^сл ^д	8	2
МЛ ^а ₂ л ^бл ^сл ^дл ^и	15	6
МЛ ^ал ^бл ^сл ^дл ^ил ^ж	30	15

Таким образом, все 15 диастереомеров ML ^ал ^бл ^сл ^дл ^ил ^ж являются киральными, тогда как для ML ^а
₂ л ^бл ^сл ^дл ^и, шесть диастереомеров являются хиральными, а три - нет (те, где L ^а они транс ). Можно видеть, что октаэдрическая координация допускает гораздо большую сложность, чем тетраэдр, который доминирует в органической химии . Тетраэдр ML ^ал ^бл ^сл ^д существует в виде одной энантиомерной пары. Для образования двух диастереомеров в органическом соединении необходимы как минимум два углеродных центра.

Отклонения от идеальной симметрии

Эффект Яна – Теллера

Этот термин также может относиться к октаэдру, находящемуся под влиянием эффекта Яна-Теллера , который является распространенным явлением, встречающимся в координационной химии . Это снижает симметрию молекулы с O _h до D _4h и известно как тетрагональное искажение.

Искаженная октаэдрическая геометрия

Некоторые молекулы, такие как XeF ₆ или IF ⁻
₆ , имеют неподеленную пару, которая искажает симметрию молекулы от O _h до C _3v . ^[4]^[5] Конкретная геометрия известна как с моношапкой октаэдр , поскольку она получена из октаэдра путем размещения неподеленной пары в центре одной треугольной грани октаэдра в качестве «шапки» (и смещения положений остальных шести атомов для ее размещения). ). ^[6] Оба они представляют собой отклонение от геометрии, предсказанной VSEPR, которая для AX ₆ E ₁ предсказывает пятиугольную пирамидальную форму.

Биоктаэдрические структуры

Пары октаэдров можно объединить таким образом, чтобы сохранить геометрию октаэдрической координации, заменяя концевые лиганды мостиковыми лигандами . Распространены два мотива слияния октаэдров: общие ребра и общие грани. Биоктаэдры с общими ребрами и гранями имеют формулы [M ₂ L ₈ (μ-L)] ₂ и M ₂ L ₆ (μ-L) ₃ соответственно. Полимерные версии одной и той же структуры связей дают стехиометрии [ML ₂ (μ-L) ₂ ] _∞ и [M(μ-L) ₃ ] _∞ соответственно.

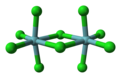
Совместное ребро или грань октаэдра дает структуру, называемую биооктаэдрической. Многие соединения пентагалогенидов и пентаалкоксидов металлов существуют в растворе и в твердом состоянии с биооктаэдрической структурой. Одним из примеров является пентахлорид ниобия . Тетрагалогениды металлов часто существуют в виде полимеров с октаэдрами, имеющими общие ребра. тетрахлорид циркония . Примером может служить ^[7] Соединения с октаэдрическими цепями с общими гранями включают MoBr ₃ , RuBr ₃ и TlBr ₃ .

Шаростержневая модель , пентахлорида ниобия биооктаэдрического координационного соединения.
Шаростержневая модель тетрахлорида циркония , неорганического полимера на основе октаэдров с общими ребрами.
Шаростержневая модель бромида молибдена (III) , неорганического полимера на основе октаэдров с общими гранями.
Посмотрите почти вниз на цепь йодида титана (III), подчеркнув затмение галогенидных лигандов в таких октаэдрах с общими гранями.

Тригонально-призматическая геометрия

Для соединений с формулой MX ₆ главной альтернативой октаэдрической геометрии является тригонально-призматическая геометрия, имеющая симметрию D _3h . В этой геометрии шесть лигандов также эквивалентны. Существуют также искаженные тригональные призмы с _{C 3v} симметрией ; ярким примером является W(СН ₃ ) ₆ . Предполагается, что взаимное превращение Δ- и Λ -комплексов, которое обычно происходит медленно, происходит через тригонально-призматический промежуточный продукт, процесс, называемый « скручиванием Байлара ». Альтернативным путем рацемизации этих же комплексов является поворот Рэя-Датта .

Расщепление d-орбитальных энергий

Для свободного иона, например газообразного Ni ²⁺ или Мо ⁰, энергии d-орбиталей равны по энергии; то есть они «выродились». В октаэдрическом комплексе это вырождение снимается. Энергия d _{z ²} и d _{х ²− и ²}, так называемые eg _- наборы, направленные непосредственно на лиганды, дестабилизируются. С другой стороны, энергия орбиталей dxz _, dxy _и dyz _, так называемого набора t2g _, стабилизируется. Метки t _2g и _eg относятся к неприводимым представлениям , которые описывают свойства симметрии этих орбиталей. Энергетическая щель, разделяющая эти два набора, является основой теории кристаллического поля и более полной теории поля лигандов . Утрата вырождения при образовании октаэдрического комплекса из свободного иона называется расщеплением кристаллического поля или расщеплением лигандного поля . Энергетическая щель обозначена Δ _o и зависит от количества и природы лигандов. Если симметрия комплекса ниже октаэдрической, _{уровни eg} и t _2g могут расщепляться дальше. Например, наборы t _2g и eg _далее расщепляются в транс -ML. ^а
₄ л ^б
₂.

Сила лигандов для этих доноров электронов имеет следующий порядок:

слабые: йод < бром < фтор < ацетат < оксалат < вода < пиридин < цианид : сильный

Так называемые «лиганды слабого поля» вызывают малые Δ _o и поглощают свет с более длинными волнами .

Реакции

Учитывая, что существует практически бесчисленное разнообразие октаэдрических комплексов, неудивительно, что описано большое разнообразие реакций. Эти реакции можно классифицировать следующим образом:

Реакции замещения лиганда (посредством различных механизмов)
Реакции присоединения лигандов, в том числе протонирование.
Окислительно-восстановительные реакции (когда электроны приобретаются или теряются)
Перегруппировки, при которых относительная стереохимия лиганда изменяется внутри координационной сферы .

Многие реакции октаэдрических комплексов переходных металлов протекают в воде. Когда анионный лиганд заменяет координированную молекулу воды, реакция называется анацией . Обратная реакция, при которой вода заменяет анионный лиганд, называется аквацией . Например, [CoCl(NH ₃ ) ₅ ] ²⁺ медленно уступает [Co(NH ₃ ) ₅ (H ₂ O)] ³⁺ в воде, особенно в присутствии кислоты или основания. Добавление концентрированной HCl превращает аквакомплекс обратно в хлорид посредством процесса анирования.

См. также

Ссылки

^ «Тригонально-бипирамидальная форма молекул @ Химический словарь и глоссарий» . глоссарий . periodni.com . Проверено 3 июля 2022 г.
^ Фон Зелевски, А. (1995). Стереохимия координационных соединений . Чичестер: Джон Уайли. ISBN 0-471-95599-Х .
^ Мисслер, Г.Л.; Тарр, Д.А. (1999). Неорганическая химия (2-е изд.). Прентис-Холл. п. 290. ИСБН 0-13-841891-8 .
^ Кроуфорд, Т. Дэниел; Спрингер, Кристен В.; Шефер, Генри Ф. (1994). «Вклад в понимание структуры гексафторида ксенона». Журнал химической физики . 102 (8): 3307–3311. Бибкод : 1995JChPh.102.3307C . дои : 10.1063/1.468642 .
^ Махджуб, Али Р.; Зеппельт, Конрад (1991). «Структура ИФ ⁻
₆ ". Applied Chemistry International Edition . 30 (3): 323–324. doi : 10.1002/anie.199103231 .
^ Зима, Марк (2015). «ВСЕПР и более шести электронных пар» . Университет Шеффилда: химический факультет . Проверено 25 сентября 2018 г. структура XeF ₆ основана на искаженном октаэдре, вероятно, в сторону одношапочного октаэдра.
^ Уэллс, А. Ф. (1984). Структурная неорганическая химия . Оксфорд: Кларендон Пресс. ISBN 0-19-855370-6 .

Внешние ссылки

[1] «Тригонально-бипирамидальная форма молекул @ Химический словарь и глоссарий» . глоссарий . periodni.com . Проверено 3 июля 2022 г.

[2] Фон Зелевски, А. (1995). Стереохимия координационных соединений . Чичестер: Джон Уайли. ISBN 0-471-95599-Х .

[3] Мисслер, Г.Л.; Тарр, Д.А. (1999). Неорганическая химия (2-е изд.). Прентис-Холл. п. 290. ИСБН 0-13-841891-8 .

[4] Кроуфорд, Т. Дэниел; Спрингер, Кристен В.; Шефер, Генри Ф. (1994). «Вклад в понимание структуры гексафторида ксенона». Журнал химической физики . 102 (8): 3307–3311. Бибкод : 1995JChPh.102.3307C . дои : 10.1063/1.468642 .

[5] Махджуб, Али Р.; Зеппельт, Конрад (1991). «Структура ИФ ⁻
₆ ". Applied Chemistry International Edition . 30 (3): 323–324. doi : 10.1002/anie.199103231 .

[6] Зима, Марк (2015). «ВСЕПР и более шести электронных пар» . Университет Шеффилда: химический факультет . Проверено 25 сентября 2018 г. структура XeF ₆ основана на искаженном октаэдре, вероятно, в сторону одношапочного октаэдра.

[7] Уэллс, А. Ф. (1984). Структурная неорганическая химия . Оксфорд: Кларендон Пресс. ISBN 0-19-855370-6 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v т и Молекулярная геометрия
Теория ВСЕПР Координационный номер
Координационный номер 2	Линейный Бент
Координационный номер 3	Тригональная плоская Трехугольная пирамидальная Т-образный
Координационный номер 4	Тетраэдрический качели Квадратный плоский
Координационный номер 5	Треугольная бипирамида Квадратно-пирамидальный Пятиугольная плоская
Координационный номер 6	Октаэдрический Треугольный призматический Пятиугольная пирамидальная
Координационный номер 7	Пятиугольная бипирамида Закрытый октаэдр Треугольно-призматический с крышкой
Координационный номер 8	Квадратный антипризматический Додекаэдрический Двуглавая треугольная призматика
Координационный номер 9	Треугольная треугольная призматика Квадратный антипризматический с крышкой
Категория