Молекулярная симметрия

В химии молекулярная симметрия описывает симметрию, присутствующую в молекулах , и классификацию этих молекул в соответствии с их симметрией. молекулы Молекулярная симметрия является фундаментальной концепцией в химии, поскольку ее можно использовать для предсказания или объяснения многих химических свойств , например наличия или отсутствия у нее дипольного момента , а также разрешенных спектроскопических переходов . Для этого необходимо использовать теорию групп . Это предполагает классификацию состояний молекулы с использованием неприводимых представлений. из таблицы символов группы симметрии молекулы. Симметрия полезна при изучении молекулярных орбиталей с приложениями к методу Хюкеля , теории поля лигандов и правилам Вудворда-Хоффмана . Во многих университетских учебниках по физической химии , квантовой химии , спектроскопии и неорганической химии обсуждается симметрия. ^[1]^[2]^[3]^[4]^[5]^[6] Другая основа более крупного масштаба — это использование кристаллических систем для описания кристаллографической симметрии в объемных материалах.

Существует множество методов определения симметрии данной молекулы, включая рентгеновскую кристаллографию и различные формы спектроскопии . Спектроскопические обозначения основаны на соображениях симметрии.

симметрии точек групп Концепции

Примеры связи киральности и симметрии
Вращательный ось ( C _n )	Неправильные элементы вращения ( S _n )
	Хиральный нет С _н	Ачирал зеркальная плоскость S ₁ = σ	Ачирал центр инверсии S ₂ = я
С ₁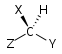
С ₂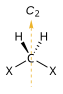

Элементы [ править ]

Точечная групповая симметрия молекулы определяется наличием или отсутствием пяти типов элементов симметрии .

Ось симметрии : ось, вокруг вращение которой ${\tfrac {360^{\circ }}{n}}$ В результате получается молекула, неотличимая от оригинала. Это также называется n -кратной осью вращения и сокращенно C _n . Примерами являются C2 _ось в воде и C3 _ось в аммиаке . Молекула может иметь более одной оси симметрии; та, у которой наибольшее n , называется главной осью и по соглашению выравнивается с осью z в декартовой системе координат .
Плоскость симметрии : плоскость отражения, посредством которой создается идентичная копия исходной молекулы. Это также называется зеркальной плоскостью и сокращенно σ (сигма = греческое «s», от немецкого «Spiegel», означающего зеркало). ^[7] У воды их два: один в плоскости самой молекулы и один перпендикулярно ей. Плоскость симметрии , параллельная главной оси, называется вертикальной (σ _v ), а перпендикулярная ей — горизонтальной (σ _h ). Существует третий тип плоскости симметрии: если вертикальная плоскость симметрии дополнительно делит пополам угол между двумя осями вращения 2-го порядка, перпендикулярными главной оси, плоскость называется двугранной (σ _d ). Плоскость симметрии также можно определить по ее декартовой ориентации, например (xz) или (yz).
Центр симметрии или центр инверсии , сокращенно i . Молекула имеет центр симметрии, когда для любого атома в молекуле существует идентичный атом, диаметрально противоположный этому центру и на равном расстоянии от него. Другими словами, молекула имеет центр симметрии, когда точки (x,y,z) и (−x,−y,−z) идентичны. Например, если в некоторой точке (x,y,z) есть атом кислорода, то в точке (−x,−y,−z) есть атом кислорода. В самом центре инверсии может быть атом, а может и не быть. Примерами являются тетрафторид ксенона (плоская квадратная молекула), центр инверсии которого находится у атома Xe, и бензол ( C
₆6Ч
₆ ), где центр инверсии находится в центре кольца.
Ось вращения-отражения : ось, вокруг которой вращение ${\tfrac {360^{\circ }}{n}}$ , с последующим отражением в перпендикулярной ему плоскости, оставляет молекулу неизмененной. называемая n -кратной несобственной осью вращения , она обозначается сокращенно Sn _Также . Примеры присутствуют в тетраэдрическом тетрафториде кремния с тремя S ₄ и шахматной конформацией этана осями с одной S ₆ осью . Ось S1 _S2 соответствует плоскости зеркала σ, а является _ось центром инверсии i . Молекула, у которой нет оси S _n ни при каком значении n, является хиральной молекулой.
Идентичность , сокращенно E , от немецкого Einheit, что означает единство. ^[8] Этот элемент симметрии просто не содержит изменений: каждая молекула имеет этот элемент симметрии, который эквивалентен собственному вращению C ₁ . Его необходимо включить в список элементов симметрии, чтобы они образовали математическую группу , определение которой требует включения единичного элемента. Оно названо так потому, что аналогично умножению на единицу (единицу). ^[9]

Операции [ править ]

XeF ₄ с плоско-квадратной геометрией имеет 1 C ₄ ось *и 4 оси C* _{2 ,} ортогональные C ₄ . перпендикулярная *оси C4* _, определяют *D4h .* _{Эти пять осей плюс зеркальная плоскость ,} группу симметрии молекулы

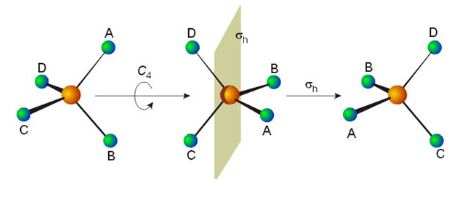
С пятью элементами симметрии связаны пять типов операций симметрии , которые делают геометрию молекулы неотличимой от исходной геометрии. Иногда их отличают от элементов симметрии кареткой или циркумфлексом . Таким образом, Ĉ _n — вращение молекулы вокруг оси, а Ê — тождественная операция. С элементом симметрии может быть связано более одной операции симметрии. Например, C ₄ оси квадратной молекулы тетрафторида ксенона (XeF ₄ ) соответствуют два вращения Ĉ ₄ в противоположных направлениях (90° и 270°), вращение Ĉ ₂ (180°) и Ĉ ₁ (0° или 270°). 360°). Поскольку Ĉ ₁ эквивалентно Ê , Ŝ ₁ — σ и Ŝ ₂ — î , все операции симметрии можно классифицировать как собственные или несобственные вращения.

Для линейных молекул вращение по часовой стрелке или против часовой стрелки вокруг оси молекулы на любой угол Φ является операцией симметрии.

Группы симметрии [ править ]

Группы [ править ]

Операции симметрии молекулы (или другого объекта) образуют группу . В математике группа — это набор с бинарной операцией , который удовлетворяет четырем свойствам, перечисленным ниже.

В группе симметрии элементы группы представляют собой операции симметрии (а не элементы симметрии), а бинарная комбинация состоит из применения сначала одной операции симметрии, а затем другой. Примером является последовательность вращения C ₄ вокруг оси z и отражения в плоскости xy, обозначаемая σ(xy) C ₄ . По соглашению порядок операций — справа налево.

Группа симметрии подчиняется определяющим свойствам любой группы.

свойство закрытия :
пары элементов x и y в G произведение * x в y также находится G. Для каждой

(в символах для каждых двух элементов x , y ∈ G , x * y также находится в G ).
Это означает, что группа закрыта , поэтому объединение двух элементов не приводит к образованию новых элементов. Операции симметрии обладают этим свойством, поскольку последовательность двух операций приведет к созданию третьего состояния, неотличимого от второго и, следовательно, от первого, так что конечный эффект на молекулу по-прежнему остается операцией симметрии. Это можно проиллюстрировать с помощью таблицы. Например, с группой точек C3 _три операции симметрии: поворот на 120°, C3 _{выполняются} , поворот на 240°, C3 _.² и поворот на 360°, что эквивалентно тождеству, E .
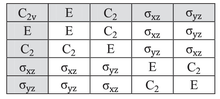
Вкладка умножения группы точек C2v
Группа точек С ₃ Таблица умножения
И С ₃ С ₃²
И И С ₃ С ₃²
С ₃ С ₃ С ₃² И
С ₃² С ₃² И С ₃
Эта таблица также иллюстрирует следующие свойства
Ассоциативное свойство :
Для каждых x , y и z в G оба результата ( x * y )* z и x *( y * z дают один и тот же элемент в G. )
(символами ( x * y )* z = x *( y * z ) для каждого x , y и z ∈ G )
существование свойства идентичности :
должен быть такой элемент (скажем, e ) В G , что произведение любого элемента G на e не вносит изменений в этот элемент.
(символами x * e = e * x = x для каждого x ∈ G )
наличие обратного элемента :
Для каждого элемента x в G должен существовать элемент y в G такой, что произведение x и y является единичным элементом e .
(в символах для каждого x ∈ G существует y ∈ G такой, что x * y = y * x = e для каждого x ∈ G )

Порядок группы — это количество элементов в группе. Для групп небольших заказов свойства группы можно легко проверить, рассмотрев ее таблицу состава — таблицу, строки и столбцы которой соответствуют элементам группы, а записи — их продуктам.

Группы точек и группы перестановок-инверсий [ править ]

Последовательное применение (или композиция ) одной или нескольких операций симметрии молекулы дает эффект, эквивалентный эффекту некоторой отдельной операции симметрии молекулы. Например, вращение C ₂ с последующим отражением σ _v рассматривается как операция симметрии σ _v ': σ _v * C ₂ = σ _v '. («Операция A , за которой следует B, чтобы сформировать C », записывается BA = C ). ^[9] Более того, набор всех операций симметрии (включая эту операцию композиции) подчиняется всем свойствам группы, приведенным выше. Итак ( S , * ) — группа, где S — множество всех операций симметрии некоторой молекулы, а * обозначает композицию (повторное применение) операций симметрии.

Эта группа называется точечной группой этой молекулы, потому что набор операций симметрии оставляет фиксированной хотя бы одну точку (хотя для некоторых симметрий целая ось или вся плоскость остается фиксированной). Другими словами, точечная группа — это группа, которая суммирует все операции симметрии, которые имеют все молекулы в этой категории. ^[9] Симметрия кристалла, напротив, описывается пространственной группой операций симметрии, включающей перемещения в пространстве.

Определить операции симметрии точечной группы конкретной молекулы можно, рассматривая геометрическую симметрию ее молекулярной модели. Однако когда для классификации состояний молекул используется точечная группа, операции в ней не следует интерпретировать одинаково. Вместо этого операции интерпретируются как вращение и/или отражение вибронных (виброэлектронных) координат. ^[10] и эти операции коммутируют с вибронным гамильтонианом. Это «операции симметрии» для этого вибронного гамильтониана. Точечная группа используется для классификации по симметрии вибронных собственных состояний жесткой молекулы. Классификация симметрии вращательных уровней, собственных состояний полного (вращательно-колебательно-электронного) гамильтониана, требует использования соответствующей группы перестановок-инверсий, введенной Лонге-Хиггинсом . ^[11] Точечные группы описывают геометрическую симметрию молекулы, тогда как группы инверсии перестановок описывают энергоинвариантную симметрию.

Примеры групп точек [ править ]

Присвоение каждой молекуле точечной группы классифицирует молекулы по категориям со схожими свойствами симметрии. Например, PCl ₃ , POF ₃ , XeO ₃ и NH ₃ используют одинаковые операции симметрии. ^[12] Все они могут подвергаться операции идентичности E , двум различным операциям вращения C ₃ и трем различным отражениям в плоскости σ _v без изменения своей идентичности, поэтому они помещаются в одну точечную группу C _3v с порядком 6. ^[9] Точно так же вода (H ₂ O) и сероводород (H ₂ S) также имеют одинаковые операции симметрии. Оба они подвергаются операции тождества E , одному C2 _{вращению} и двум отражениям σv _{изменения} своей идентичности, поэтому они оба помещаются в одну точечную группу C2v _без с порядком 4. ^[13] Эта система классификации помогает ученым более эффективно изучать молекулы, поскольку химически связанные молекулы в одной и той же точечной группе имеют тенденцию демонстрировать схожие схемы связей, диаграммы молекулярных связей и спектроскопические свойства. ^[9]Симметрия точечной группы описывает симметрию молекулы, когда она зафиксирована в равновесной конфигурации в определенном электронном состоянии. Он не допускает ни туннелирования между минимумами, ни изменения формы, которое может возникнуть из-за эффектов центробежного искажения молекулярного вращения.

Группы общих точек [ править ]

В следующей таблице перечислены многие точечные группы , применимые к молекулам, помеченные с использованием обозначения Шенфлиса , которое распространено в химии и молекулярной спектроскопии. Описания включают общие формы молекул, которые можно объяснить моделью VSEPR . В каждой строке описания и примеры не имеют более высоких симметрий, а это означает, что именованная группа точек охватывает все симметрии точек.

Группа точек	Операции симметрии ^[14]	Простое описание типичной геометрии	Пример 1	Пример 2	Пример 3
С ₁	И	нет симметрии, хиральный	бромхлорфторметан оба энантиомера ( показаны )	лизергиновая кислота	L-лейцин и большинство других α- аминокислот, кроме глицина.
С _с	E σ _ч	зеркальная плоскость	тионилхлорид	хлорноватистая кислота	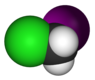хлориодометан
C_Там	Э я	центр инверсии	мезо -винная кислота	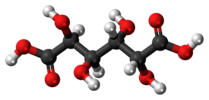слизевая кислота ( мезо -галактаровая кислота)	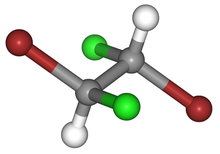1,2 дибром 1,2 дихлорэтан
C _∞v	Е 2 С _∞^Ф ∞σ _v	линейный	фтористый водород (и все другие гетероядерные двухатомные молекулы )	закись азота (окись азота)	синильная кислота (цианистый водород)
D _∞h	Е 2 С _∞^Ф ∞σ _i i 2 S _∞^Ф ∞ C ₂	линейный с центром инверсии	кислород (и все другие гомоядерные двухатомные молекулы)	углекислый газ	ацетилен (этин)
С ₂	Е С ₂	«геометрия открытой книги», хиральная	перекись водорода	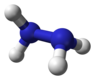гидразин	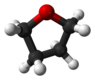тетрагидрофуран (твист-конформация)
С ₃	Е С ₃ С ₃²	пропеллер, хиральный	трифенилфосфин	триэтиламин	фосфорная кислота
С _{2 часа}	E C ₂ я σ _час	плоский с центром инверсии, без вертикальной плоскости	транс - 1,2-дихлорэтилен	транс - дифторид азота	транс - азобензол
С _{2 в}	E C ₂ σ _v (xz) σ _v '(yz)	угловой (H ₂ O) или качающийся (SF ₄ )	вода	тетрафторид серы	дихлорметан
С _{3 часа}	Е С ₃ С ₃² σ S₃ S_hS3S3⁵	пропеллер	борная кислота	флороглюцинол (1,3,5-тригидроксибензол)	бензотрифуроксан
С _3В	Е 2 С ₃ 3σ _v	тригонально-пирамидальный	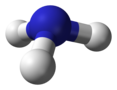аммиак (если инверсией пирамиды пренебречь )	оксихлорид фосфора	тетракарбонилгидрид кобальта , HCo(CO) ₄
С _4В	Е 2 С ₄ С ₂ 2σ _v 2σ _d	квадратно-пирамидальный	окситетрафторид ксенона	пентаборан(9) , B ₅ H ₉	нитропруссид-анион [Fe(CN) ₅ (NO)] ²⁻
С ₅	Е 2 С ₅ 2 С ₅²	пятикратная вращательная симметрия	С-реактивный белок	[Fe(Me ₅ -Cp)(P ₅ )]	Производное кораннулена
С _5В	Е 2 С ₅ 2 С ₅² 5σ _в	комплекс «доильный стул»	Циклопентадиенилникельнитрозил (CpNiNO)	кораннулен	Пентаметилциклопентадиенилникельнитрозил (Cp*NiNO)
D_Д2	Е С ₂ (х) С ₂ (у) С ₂ (з)	твист, хиральный	бифенил (косая конформация)	твистан (C ₁₀ H ₁₆ )	(δ,δ)- транс- [Co(en) ₂ Cl ₂ ] ⁺
Д ₃	Е В ₃ (з) 3 В ₂	тройная спираль, хиральная	Катион трис(этилендиамин)кобальта(III)	анион трис(оксалато)железа(III)	трис(ен)кобальт(III)
Д _{2 часа}	E C ₂ (z) C ₂ (y) C ₂ (x) i σ(xy) σ(xz) σ(yz)	плоская с центром инверсии, вертикальная плоскость	этилен	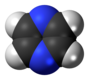пиразин	диборан
Д _{3 часа}	E 2 C ₃ 3 C ₂ σ _h 2 S ₃ 3σ _v	тригонально-плоскостной или тригонально-бипирамидальный	трифторид бора	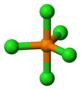пентахлорид фосфора	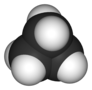циклопропан
Д _{4 часа}	E 2 C ₄ C ₂ 2 C ₂ ' 2 C ₂ " i 2 S ₄ σ _h 2σ _v 2σ _d	квадратный плоский	тетрафторид ксенона	октахлордимолибдат(II) анион	Транс -[Ко ^III(NH ₃ ) ₄ Cl ₂ ] ⁺ (исключая атомы H)
Д _5ч	Е 2 С ₅ 2 С ₅² 5 С ₂ σ _ч 2 С ₅ 2 С ₅³ 5σ _в	пятиугольный	циклопентадиенильный анион	рутеноцен	С ₇₀
Д _6ч	E 2 C ₆ 2 C ₃ C ₂ 3 C ₂ ' 3 C ₂ '' i 2 S ₃ 2 S ₆ σ _h 3σ _d 3σ _v	шестиугольный	бензол	бис(бензол)хром	коронен ( C ₂₄ H ₁₂ )
Д _7ч.	E C ₇ S ₇ 7 C ₂ σ _h 7σ _v	семиугольный	тропилий ( C ₇ H ₇⁺) катион
Д _8ч.	E C ₈ C ₄ C ₂ S ₈ i 8 C ₂ σ _h 4σ _v 4σ _d	восьмиугольный	циклооктатетраенид ( C ₈ H ₈²⁻) анион	ураноцен	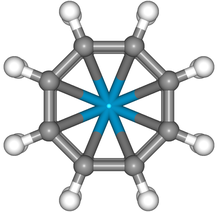бис(кот)торий(IV)
Д _2д	Е 2 S ₄ C ₂ 2 C ₂ ' 2σ _d	поворот на 90°	один	тетранитрид тетрасеры	диборан(4) (возбужденное состояние)
Д _3д	Е 2 С ₃ 3 С ₂ я 2 С ₆ 3σ _г	поворот на 60°	этан (шахматный ротамер )	октакарбонил дикобальта (немостиковый изомер )	конформация циклогексанового стула
Д _4д	Е 2 С ₈ 2 С ₄ 2 С ₈³ С ₂ 4 С ₂ ' 4σ _г	поворот на 45°	сера (коронная конформация S ₈ )	декакарбонил димарганца (шахматный ротамер)	октафтороксенат-ион (идеализированная геометрия)
Д _5д	Е 2 С ₅ 2 С ₅² 5 С ₂ и 2 С ₁₀³ 2 С ₁₀ 5σ _г	поворот на 36°	ферроцен (шахматный ротамер)	Рутеноцен (олень)	фуллерид-ион
С ₄	Э 2 С ₄ С ₂		1,2,3,4-тетрафторспиропентан ( мезоизомер ) ^[15]	тетраметил-кот	бис(дт)медь(I)
Т _д	Е 8 С ₃ 3 С ₂ 6 С ₄ 6σ _г	четырехгранный	метан	пятиокись фосфора	адамантан
Т _ч	Е 4 С ₃ 4 С ₃² я 3 С ₂ 4 С ₆ 4 С ₆⁵ 3σ _ч	пиритоэдр	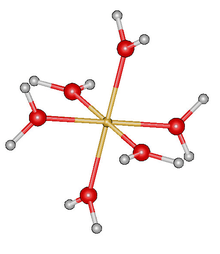[Fe(C ₅ H ₅ N) ₆ ] ²⁺	[Тх(НО ₃ ) ₆ ] ^2-	Fe(H2O)6
Ой	E 8 C ₃ 6 C ₂ 6 C ₄ 3 C ₂ i 6 S ₄ 8 S ₆ 3σ _h 6σ _d	октаэдрический или кубический	гексафторид серы	гексакарбонил молибдена	Кубинский
я	Е 12 С ₅ 12 С ₅² 20 С ₃ 15 С ₂	хиральный икосаэдр или додекаэдр	Риновирус	курносый додекаэдр	вирус полиомиелита человека
I _h	Е 12 С ₅ 12 С ₅² 20 С ₃ 15 С ₂ и 12 С ₁₀ 12 С ₁₀³ 20 С ₆ 15σ	икосаэдрический или додекаэдрический	Бакминстерфуллерен	додекаборат-анион	додекаэдр

Представления [ править ]

Набор матриц , которые умножаются друг на друга способом, имитирующим таблицу умножения элементов группы, называется представлением группы. Например, для точечной группы C _2v следующие три матрицы являются частью представления группы:

\underbrace {\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{C_{2}}\times \underbrace {\begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{\sigma _{\text{v}}}=\underbrace {\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}} _{\sigma '_{\text{v}}}

Хотя существует бесконечное число таких представлений, неприводимые представления (или «иррепы») группы — это все, что необходимо, поскольку все другие представления группы можно описать как прямую сумму неприводимых представлений.Кроме того, неприводимые представления — это те матричные представления, в которых матрицы имеют наиболее возможную диагональную форму.

Таблицы символов [ править ]

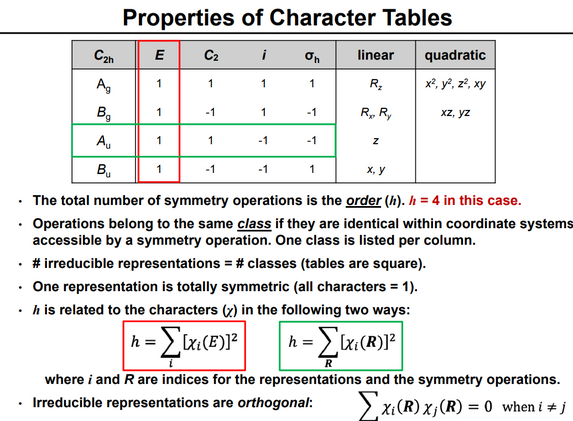
Для любой группы ее таблица характеров дает табуляцию (для классов группы) характеров (суммы диагональных элементов) матриц всех неприводимых представлений группы. Поскольку количество неприводимых представлений равно количеству классов, таблица символов имеет квадратную форму.

Представления помечены в соответствии с рядом соглашений:

А, когда вращение вокруг главной оси симметрично
Б, когда вращение вокруг главной оси асимметрично
E и T — дважды и трижды вырожденные представления соответственно.
когда группа точек имеет центр инверсии, индекс g ( немецкий : gerade или даже) сигнализирует об отсутствии изменения знака, а индекс u ( унгераде или нечетный) — об изменении знака относительно инверсии.
с точечными группами C _∞v и D _∞h символы заимствованы из углового момента описания : Σ , Π , Δ .

Таблицы также содержат информацию о том, как декартовы базисные векторы, вращения вокруг них и квадратичные функции от них преобразуются с помощью операций симметрии группы, отмечая, какое неприводимое представление преобразуется таким же образом. Эти обозначения традиционно располагаются в правой части таблиц. Эта информация полезна, поскольку химически важные орбитали (в частности, p- и d -орбитали) имеют ту же симметрию, что и эти объекты.

Таблица символов для точечной группы симметрии C _2v приведена ниже:

С _{2 в}	И	С ₂	σ _v (xz)	с _в '(ыз)
А ₁	1	1	1	1	С	х ², и ², С ²
А ₂	1	1	−1	−1	Р _з	ху
Б ₁	1	−1	1	−1	х , р _у	хз
B_Б2	1	−1	−1	1	у , р _х	да

Рассмотрим пример воды (H ₂ O), которая имеет описанную выше симметрию C _2v . 2 p _x Орбиталь кислорода _{имеет симметрию B 1} , как указано в четвертой строке таблицы символов выше, с x в шестом столбце). Он ориентирован перпендикулярно плоскости молекулы и меняет знак при операциях C ₂ и σ _v '(yz), но остается неизменным при двух других операциях (очевидно, что символ операции тождества всегда равен +1). Таким образом, набор символов этой орбитали равен {1, −1, 1, −1}, что соответствует неприводимому представлению B ₁ . Аналогичным образом видно, что орбиталь 2 p _z имеет симметрию неприводимого представления A ₁ ( т. е .: ни одна из операций симметрии не меняет его), 2 p _y B ₂ и орбиталь 3 d _xy A ₂ . Эти и другие назначения отмечены в двух крайних правых столбцах таблицы.

Историческая справка [ править ]

Ганс Бете использовал характеры операций с точечными группами в своем исследовании теории поля лигандов в 1929 году, а Юджин Вигнер использовал теорию групп для объяснения правил отбора в атомной спектроскопии . ^[16] Первые таблицы характеров были составлены Ласло Тисой (1933) в связи с колебательными спектрами. Роберт Малликен первым опубликовал таблицы характеров на английском языке (1933), а Э. Брайт Уилсон использовал их в 1934 году для предсказания симметрии нормальных мод колебаний . ^[17] Полный набор из 32 кристаллографических точечных групп был опубликован в 1936 году Розенталем и Мерфи. ^[18]

Симметрия колебательных мод [ править ]

Каждая нормальная мода молекулярных колебаний обладает симметрией, которая составляет основу одного неприводимого представления группы симметрии молекулы. ^[19] Например, молекула воды имеет три нормальных режима вибрации: симметричное растяжение, при котором длины двух связей OH изменяются в фазе друг относительно друга, асимметричное растяжение, при котором они изменяются в противофазе, и изгиб, при котором меняется валентный угол. Молекулярная симметрия воды C _2v с четырьмя неприводимыми представлениями A ₁ , A ₂ , B ₁ и B ₂ . Симметричные моды растяжения и изгиба имеют симметрию A ₁ , а несимметричная мода имеет симметрию B ₂ . Таким образом, общая симметрия трех колебательных мод равна Γ _vib = 2A ₁ + B ₂ . ^[19]^[20]

Колебательные моды аммиака [ править ]

Молекулярная симметрия аммиака C _3v . Число колебательных мод можно найти, используя формулу 3N-6 для нелинейной молекулы. Итак, у него есть шесть вибрационных режимов. Он имеет _{E, C 3} и σ _v операции симметрии . ^[7] Движение атома азота и трех атомов водорода относительно друг друга порождает эти моды. Все три атома водорода движутся симметрично вдоль оси молекулы либо в направлении атома азота, либо от него. Этот режим известен как симметричное растяжение (v₁). Симметрия растяжения связи NH отражается в этом растягивающем движении. Из трех колебательных режимов этот имеет самую высокую частоту . ^[21]

В конфигурации изгиба (ν₂) атом азота остается неподвижным, в то время как три атома водорода движутся в разных направлениях друг от друга. В результате этого действия происходят изменения валентных углов, в том числе изгиб молекулы из плоскости. Из-за того, что атомы водорода движутся как зонтик, этот режим часто называют «режимом зонтика». ^[23] Асимметричное растяжение (ν₃) также называют режимом асимметричного растяжения. Пока один атом приближается к атому азота , два атома водорода в этом режиме раздвигаются.

Аммиак имеет четыре атома. Каждому атому соответствует три вектора . NH ₃ имеет три неприводимых представления A ₁ , A ₂ и E. Суммарные моды вибрации включают колебательные, вращательные и поступательные моды.

Всего мод = 3A1 ₊ A2 ₊ 4E

Режимы вращения = А ₂ + Е

Трансляционные режимы = A ₁ + E

Колебательные режимы = Суммарные режимы - Вращательные режимы - Поступательные режимы = 3А ₁ + А ₂ + 4Е - А ₂ - Е - А ₁ - Е = 2А ₁ + 2Е

Еще примеры [ править ]

W(CO) ₆ имеет октаэдрическую геометрию. Неприводимое представление валентного колебания CO: A _1g + E _g + T _1u . Из них только T _1u является ИК-активным.
B ₂ H ₆ ( диборан ) имеет молекулярную симметрию D _2h . Концевые валентные колебания BH, активные в ИК, — это B _2u и B _3u .

Fac-Mo(CO) ₃ (CH ₃ CH ₂ CN) ₃ имеет _{C 3v} геометрию . Неприводимым представлением валентных колебаний CO является A ₁ + E. Оба из них являются ИК-активными.

Симметрия молекулярных орбиталей [ править ]

Каждая молекулярная орбиталь также обладает симметрией одного неприводимого представления. Например, этилен (C ₂ H ₄ ) имеет группу симметрии D _2h , а его высшая занятая молекулярная орбиталь ( ВЗМО ) является связывающей пи-орбиталью, которая составляет основу его неприводимого представления B _1u . ^[24]

вращение и молекулярная нежесткость Молекулярное

Как обсуждалось выше в разделе « Группы точек» и «группы перестановок-инверсий», точечные группы полезны для классификации колебательных и электронных состояний жестких молекул (иногда называемых полужесткими молекулами), которые испытывают лишь небольшие колебания относительно одной равновесной геометрии. Лонге-Хиггинс ввел более общий тип группы симметрии. ^[11] подходит не только для классификации колебательных и электронных состояний жестких молекул, но также для классификации их вращательных и ядерных спиновых состояний. Кроме того, такие группы можно использовать для классификации состояний нежестких (или флюксиальных ) молекул, которые туннелируют между эквивалентными геометриями (так называемые версии). ^[25]) и учесть искажающие эффекты вращения молекул. Эти группы известны как группы перестановок-инверсий , поскольку операции симметрии в них представляют собой энергетически осуществимые перестановки одинаковых ядер, или инверсию относительно центра масс ( операция четности ), или их комбинацию.

Например, этан (C ₂ H ₆ ) имеет три эквивалентные шахматные конформации . Туннелирование между конформациями происходит при обычных температурах за счет внутреннего вращения одной метильной группы относительно другой. не вращение всей молекулы вокруг оси С3 _Это . Хотя каждая конформация имеет симметрию D _3d , как показано в таблице выше, описание внутреннего вращения и связанных с ним квантовых состояний и энергетических уровней требует более полной группы перестановок-инверсий G ₃₆ . ^[26]

Точно так же аммиак (NH ₃ ) имеет две эквивалентные пирамидальные ( C _3v ) конформации, которые взаимопревращаются в результате процесса, известного как инверсия азота . Это не операция инверсии точечной группы, которую я использовал для центросимметричных жестких молекул (т.е. инверсия колебательных смещений и электронных координат в ядерном центре масс), поскольку NH ₃ не имеет центра инверсии и не является центросимметричным. Скорее, это инверсия ядерных и электронных координат в центре масс молекулы (иногда называемая операцией четности), которая оказывается энергетически осуществимой для этой молекулы. Подходящей группой перестановок-инверсий, которую следует использовать в этой ситуации, является D _3h (M). ^[27] которая изоморфна точечной группе D _3h .

Кроме того, в качестве примеров можно привести метан (CH ₄ ) и H ₃⁺ молекулы имеют высокосимметричные равновесные структуры с T _d и D _3h симметрией точечной группы соответственно; у них отсутствуют постоянные электрические дипольные моменты, но они имеют очень слабые спектры чистого вращения из-за вращательного движения.центробежное искажение. ^[28]^[29] Группы перестановок-инверсий, необходимые для полного изучения CH ₄ и H ₃⁺ Т ( М _д ) ^[30] и Д _3h (М) соответственно.

В основном (N) электронном состоянии молекула этилена C ₂ H ₄ имеет симметрию точечной группы D _2h , тогда как в возбужденном (V) состоянии она имеет D _2d симметрию . Чтобы рассматривать эти два состояния вместе, необходимо допустить кручение и использовать двойную группу группы перестановок-инверсий G ₁₆ . ^[31]

Второй, менее общий подход к симметрии нежестких молекул принадлежит Альтману. ^[32]^[33] В этом подходе группы симметрии известны как супергруппы Шредингера и состоят из двух типов операций (и их комбинаций): (1) операций геометрической симметрии (вращений, отражений, инверсий) жестких молекул и (2) изодинамических операций , которые перевести нежесткую молекулу в энергетически эквивалентную форму с помощью физически разумного процесса, такого как вращение вокруг одинарной связи (как в этане) или молекулярная инверсия (как в аммиаке). ^[33]

См. также [ править ]

Ссылки [ править ]

^ Квантовая химия , 3-е изд. Джон П. Лоу, Кирк Петерсон ISBN 0-12-457551-X
^ Физическая химия: молекулярный подход Дональда А. МакКуорри, Джона Д. Саймона ISBN 0-935702-99-7
^ Химическая связь , 2-е изд. Дж. Н. Мюррелл, СФА Кеттл, Дж. М. Теддер ISBN 0-471-90760-X
^ Физическая химия , 8-е изд. П. В. Аткинс и Дж. де Паула, У. Х. Фриман, 2006 г. ISBN 0-7167-8759-8 , глава 12.
^ Г.Л. Мисслер и Д.А. Тарр Неорганическая химия , 2-е изд. Пирсон, Прентис Холл, 1998 г. ISBN 0-13-841891-8 , гл.4.
^ Молекулярная симметрия и спектроскопия , 2-е изд. Филип Р. Банкер и Пер Дженсен, NRC Research Press, Оттава (1998) [1] ISBN 9780660196282
↑ Перейти обратно: Перейти обратно: ^а ^б «Операции симметрии и таблицы символов» . Университет Эксетера . 2001 . Проверено 29 мая 2018 г.
^ Результаты LEO для «единства»
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Пфеннинг, Брайан (2015). Основы неорганической химии . Джон Уайли и сыновья. ISBN 9781118859025 .
^ PR Bunker и П. Дженсен (2005), Основы молекулярной симметрии (CRC Press) ISBN 0-7503-0941-5 [2] Раздел 8.3
↑ Перейти обратно: Перейти обратно: ^а ^б Лонге-Хиггинс, ХК (1963). «Группы симметрии нежестких молекул» . Молекулярная физика . 6 (5): 445–460. Бибкод : 1963МолФ...6..445Л . дои : 10.1080/00268976300100501 .
^ Пфенниг, Брайан (30 марта 2015 г.). Основы неорганической химии . Уайли. п. 191. ИСБН 978-1-118-85910-0 .
^ Мисслер, Гэри (2004). Неорганическая химия . Пирсон. ISBN 9780321811059 .
^ Мисслер, Гэри Л.; Тарр, Дональд А. (1999). «Таблицы символов (все, кроме D7h)». Неорганическая химия (2-е изд.). Прентис-Холл. стр. 621–630. ISBN 0-13-841891-8 .
^ Хаускрофт, CE; Шарп, AG (2008). Неорганическая химия (3-е изд.). Прентис Холл. стр. 111–112. ISBN 978-0-13-175553-6 .
^ Теория групп и ее применение к квантовой механике атомных спектров , EP Wigner, Academic Press Inc. (1959)
^ Исправление двух давних ошибок в таблицах символов симметрии точечных групп Рэндалл Б. Ширтс J. Chem. Образование. 2007, 84, 1882. Аннотация.
^ Розенталь, Дженни Э.; Мерфи, генеральный менеджер (1936). «Теория групп и колебания многоатомных молекул». Преподобный Мод. Физ . 8 (4): 317–346. Бибкод : 1936РвМП....8..317Р . дои : 10.1103/RevModPhys.8.317 .
↑ Перейти обратно: Перейти обратно: ^а ^б Харрис, Дэниел С.; Бертолуччи, Майкл Д. (1978). «3». Симметрия и спектроскопия . Издательство Оксфордского университета. стр. 138–142. ISBN 0-19-502001-4 . Каждая нормальная мода вибрации образует базисный набор для неприводимого представления точечной группы молекулы.
^ Г.Л. Мисслер и Д.А. Тарр Неорганическая химия , 2-е изд. Пирсон, Прентис Холл, 1998 г. ISBN 0-13-841891-8 , стр. 97-100.
^ «Колебательные моды аммиака» . www.chem.purdue.edu . Проверено 13 апреля 2024 г.
^ Гринвуд, Нью-Йорк; Эрншоу, А. (1997) Химия элементов (2 ^nd ред.), Oxford: Butterworth-Heinemann, стр. стр. 423 ISBN 0-7506-3365-4
^ «Зонтичный режим — Большая Химическая Энциклопедия» . chempedia.info . Проверено 13 апреля 2024 г.
^ Харрис, Дэниел С.; Бертолуччи, Майкл Д. (1978). «4». Симметрия и спектроскопия . Издательство Оксфордского университета. п. 278. ИСБН 0-19-502001-4 .
^ Кость, РГА; и др. (1991). «Переходные состояния из групп молекулярной симметрии: анализ нежесткого ацетиленового тримера». Молекулярная физика . 72 (1): 33–73. Бибкод : 1991МолФ..72...33Б . дои : 10.1080/00268979100100021 .
^ PR Бункер (1964). «Волновые функции вращения-торсиона молекул, имеющих два одинаковых ротора». Мол. Физ . 8 : 81. дои : 10.1080/00268976400100091 .
^ PR Bunker «Практически все, что вам следует знать о Группе молекулярной симметрии»в «Колебательных спектрах и структуре», Vol. III', изд. Джеймс Р. Дуриг, Марсель Деккер (1975) ISBN 0824711491
^ Уотсон, JKG (1971). «Запрещенные вращательные спектры многоатомных молекул». Журнал молекулярной спектроскопии . 40 (3): 546–544. Бибкод : 1971JMoSp..40..536W . дои : 10.1016/0022-2852(71)90255-4 .
^ Олдани, М.; и др. (1985). «Чистые вращательные спектры метана и метана-d4 в основном колебательном состоянии, наблюдаемые методом микроволновой спектроскопии с преобразованием Фурье». Журнал молекулярной спектроскопии . 110 (1): 93–105. Бибкод : 1985JMoSp.110...93O . дои : 10.1016/0022-2852(85)90215-2 .
^ PR Бункер; Пер Йенсен (1999). «Молекулы сферического верха и группа симметрии молекул». Мол. Физ . 97 (1–2): 255. Бибкод : 1999MolPh..97..255B . дои : 10.1080/00268979909482827 .
^ Уотсон, JKG; и др. (1996). «Теория нечетных крутильных переходов в V−N-резонансном спектре комбинационного рассеяния этилена» . J Chem Phys . 105 (4): 1348. Бибкод : 1996JChPh.105.1348W . дои : 10.1063/1.472001 .
^ Альтманн С.Л. (1977) Индуцированные представления в кристаллах и молекулах , Academic Press
↑ Перейти обратно: Перейти обратно: ^а ^б Flurry, RL (1980) Группы симметрии , Прентис-Холл, ISBN 0-13-880013-8 , стр. 115-127.

Внешние ссылки [ править ]

Симметрия точечной группы @ Университет Ньюкасла
Молекулярная симметрия @ Имперский колледж Лондона
Таблицы симметрии молекулярных групп точек
Таблицы символов для групп точек по химии
Молекулярная симметрия онлайн @ Открытый университет Израиля
Интернет-курс лекций по молекулярной симметрии @ Bergische Universitaet
ДЕКОР – Симметрия @ Кембриджский центр кристаллографических данных
Подробности связи между точечными группами и группами инверсии перестановок , Филип Банкер

[1] Квантовая химия , 3-е изд. Джон П. Лоу, Кирк Петерсон ISBN 0-12-457551-X

[2] Физическая химия: молекулярный подход Дональда А. МакКуорри, Джона Д. Саймона ISBN 0-935702-99-7

[3] Химическая связь , 2-е изд. Дж. Н. Мюррелл, СФА Кеттл, Дж. М. Теддер ISBN 0-471-90760-X

[4] Физическая химия , 8-е изд. П. В. Аткинс и Дж. де Паула, У. Х. Фриман, 2006 г. ISBN 0-7167-8759-8 , глава 12.

[5] Г.Л. Мисслер и Д.А. Тарр Неорганическая химия , 2-е изд. Пирсон, Прентис Холл, 1998 г. ISBN 0-13-841891-8 , гл.4.

[6] Молекулярная симметрия и спектроскопия , 2-е изд. Филип Р. Банкер и Пер Дженсен, NRC Research Press, Оттава (1998) [1] ISBN 9780660196282

[:1-7] Перейти обратно: Перейти обратно: ^а ^б «Операции симметрии и таблицы символов» . Университет Эксетера . 2001 . Проверено 29 мая 2018 г.

[8] Результаты LEO для «единства»

[:0-9] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Пфеннинг, Брайан (2015). Основы неорганической химии . Джон Уайли и сыновья. ISBN 9781118859025 .

[10] PR Bunker и П. Дженсен (2005), Основы молекулярной симметрии (CRC Press) ISBN 0-7503-0941-5 [2] Раздел 8.3

[Longuet-Higgins1963-11] Перейти обратно: Перейти обратно: ^а ^б Лонге-Хиггинс, ХК (1963). «Группы симметрии нежестких молекул» . Молекулярная физика . 6 (5): 445–460. Бибкод : 1963МолФ...6..445Л . дои : 10.1080/00268976300100501 .

[12] Пфенниг, Брайан (30 марта 2015 г.). Основы неорганической химии . Уайли. п. 191. ИСБН 978-1-118-85910-0 .

[13] Мисслер, Гэри (2004). Неорганическая химия . Пирсон. ISBN 9780321811059 .

[14] Мисслер, Гэри Л.; Тарр, Дональд А. (1999). «Таблицы символов (все, кроме D7h)». Неорганическая химия (2-е изд.). Прентис-Холл. стр. 621–630. ISBN 0-13-841891-8 .

[15] Хаускрофт, CE; Шарп, AG (2008). Неорганическая химия (3-е изд.). Прентис Холл. стр. 111–112. ISBN 978-0-13-175553-6 .

[16] Теория групп и ее применение к квантовой механике атомных спектров , EP Wigner, Academic Press Inc. (1959)

[17] Исправление двух давних ошибок в таблицах символов симметрии точечных групп Рэндалл Б. Ширтс J. Chem. Образование. 2007, 84, 1882. Аннотация.

[18] Розенталь, Дженни Э.; Мерфи, генеральный менеджер (1936). «Теория групп и колебания многоатомных молекул». Преподобный Мод. Физ . 8 (4): 317–346. Бибкод : 1936РвМП....8..317Р . дои : 10.1103/RevModPhys.8.317 .

[Harris-19] Перейти обратно: Перейти обратно: ^а ^б Харрис, Дэниел С.; Бертолуччи, Майкл Д. (1978). «3». Симметрия и спектроскопия . Издательство Оксфордского университета. стр. 138–142. ISBN 0-19-502001-4 . Каждая нормальная мода вибрации образует базисный набор для неприводимого представления точечной группы молекулы.

[20] Г.Л. Мисслер и Д.А. Тарр Неорганическая химия , 2-е изд. Пирсон, Прентис Холл, 1998 г. ISBN 0-13-841891-8 , стр. 97-100.

[21] «Колебательные моды аммиака» . www.chem.purdue.edu . Проверено 13 апреля 2024 г.

[22] Гринвуд, Нью-Йорк; Эрншоу, А. (1997) Химия элементов (2 ^nd ред.), Oxford: Butterworth-Heinemann, стр. стр. 423 ISBN 0-7506-3365-4

[23] «Зонтичный режим — Большая Химическая Энциклопедия» . chempedia.info . Проверено 13 апреля 2024 г.

[24] Харрис, Дэниел С.; Бертолуччи, Майкл Д. (1978). «4». Симметрия и спектроскопия . Издательство Оксфордского университета. п. 278. ИСБН 0-19-502001-4 .

[25] Кость, РГА; и др. (1991). «Переходные состояния из групп молекулярной симметрии: анализ нежесткого ацетиленового тримера». Молекулярная физика . 72 (1): 33–73. Бибкод : 1991МолФ..72...33Б . дои : 10.1080/00268979100100021 .

[26] PR Бункер (1964). «Волновые функции вращения-торсиона молекул, имеющих два одинаковых ротора». Мол. Физ . 8 : 81. дои : 10.1080/00268976400100091 .

[27] PR Bunker «Практически все, что вам следует знать о Группе молекулярной симметрии»в «Колебательных спектрах и структуре», Vol. III', изд. Джеймс Р. Дуриг, Марсель Деккер (1975) ISBN 0824711491

[28] Уотсон, JKG (1971). «Запрещенные вращательные спектры многоатомных молекул». Журнал молекулярной спектроскопии . 40 (3): 546–544. Бибкод : 1971JMoSp..40..536W . дои : 10.1016/0022-2852(71)90255-4 .

[29] Олдани, М.; и др. (1985). «Чистые вращательные спектры метана и метана-d4 в основном колебательном состоянии, наблюдаемые методом микроволновой спектроскопии с преобразованием Фурье». Журнал молекулярной спектроскопии . 110 (1): 93–105. Бибкод : 1985JMoSp.110...93O . дои : 10.1016/0022-2852(85)90215-2 .

[30] PR Бункер; Пер Йенсен (1999). «Молекулы сферического верха и группа симметрии молекул». Мол. Физ . 97 (1–2): 255. Бибкод : 1999MolPh..97..255B . дои : 10.1080/00268979909482827 .

[31] Уотсон, JKG; и др. (1996). «Теория нечетных крутильных переходов в V−N-резонансном спектре комбинационного рассеяния этилена» . J Chem Phys . 105 (4): 1348. Бибкод : 1996JChPh.105.1348W . дои : 10.1063/1.472001 .

[32] Альтманн С.Л. (1977) Индуцированные представления в кристаллах и молекулах , Academic Press

[Flurry-33] Перейти обратно: Перейти обратно: ^а ^б Flurry, RL (1980) Группы симметрии , Прентис-Холл, ISBN 0-13-880013-8 , стр. 115-127.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]