Электронная плотность

Эта статья о квантовомеханической плотности вероятности электрона. О плотности числа электронов в плазме, также называемой «электронной плотностью», см. Плазма (физика) .

Электронная плотность или электронная плотность — это мера вероятности присутствия электрона в бесконечно малом элементе пространства, окружающем любую данную точку. Это скалярная величина, зависящая от трех пространственных переменных, и обычно обозначается либо как $\rho ({\textbf {r}})$ или $n({\textbf {r}})$. Плотность определяется по определению нормализованным $N$ электрона - волновая функция , которая сама зависит от $4N$ переменные ( ${\textstyle 3N}$ пространственный и $N$ спиновые координаты). И наоборот, плотность определяет волновую функцию по модулю с точностью до фазового множителя, обеспечивая формальную основу теории функционала плотности .

Согласно квантовой механике , из-за принципа неопределенности в атомном масштабе невозможно предсказать точное местоположение электрона, а только вероятность его нахождения в заданном положении; поэтому электроны в атомах и молекулах действуют так, как будто они «размазаны» в пространстве. Для одноэлектронных систем плотность электронов в любой точке пропорциональна квадрату величины волновой функции .

Обзор

В молекулах обычно находятся области с большой электронной плотностью вокруг атома и его связей . В делокализованных или сопряженных системах , таких как фенол , бензол и такие соединения, как гемоглобин и хлорофилл , электронная плотность значительна во всей области, т. е. в бензоле они находятся выше и ниже плоского кольца. Иногда это изображают схематически как серию чередующихся одинарных и двойных связей. В случае фенола и бензола кружок внутри шестиугольника показывает делокализованную природу соединения. Это показано ниже:

Mesomeric structures of phenol

В соединениях с несколькими взаимосвязанными кольцевыми системами это уже неточно, поэтому используются чередующиеся одинарные и двойные связи. В таких соединениях, как хлорофилл и фенол, на некоторых диаграммах показана пунктирная или пунктирная линия, обозначающая делокализацию областей, где электронная плотность выше рядом с одинарными связями. Сопряженные системы иногда могут представлять собой области, где электромагнитное излучение поглощается на разных длинах волн, в результате чего соединения кажутся окрашенными. В полимерах эти области известны как хромофоры.

В квантово-химических расчетах плотность электронов ρ( r ) является функцией координат r , определяемой так: ρ( r )d r — это количество электронов в небольшом объёме d r . Для с закрытой оболочкой молекул $\rho (\mathbf {r} )$ может быть записано через сумму произведений базисных функций φ:

$\rho (\mathbf {r} )=\sum _{\mu }\sum _{\nu }P_{\mu \nu }\phi _{\mu }(\mathbf {r} )\phi _{\nu }(\mathbf {r} )$

Электронная плотность рассчитана для анилина . Высокие значения плотности указывают положение атомов, промежуточные значения плотности подчеркивают связь , низкие значения предоставляют информацию о форме и размере молекулы.

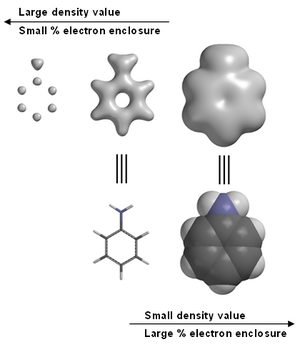
где P — матрица плотности . Плотность электронов часто выражается в виде изоповерхности (поверхности изоплотности), при этом размер и форма поверхности определяются значением выбранной плотности, или в процентах от общего количества заключенных электронов.

Программное обеспечение для молекулярного моделирования часто предоставляет графические изображения электронной плотности. Например, в анилине (см. изображение справа). Графические модели, включая электронную плотность, являются широко используемым инструментом в образовании по химии. Обратите внимание, что на крайнем левом изображении анилина высокие плотности электронов связаны с атомами углерода и азота , но атомы водорода , имеющие только один протон в ядрах, не видны. Это причина того, что рентгеновская дифракция затрудняет определение положения водорода.

Большинство пакетов программного обеспечения для молекулярного моделирования позволяют пользователю выбирать значение электронной плотности, часто называемое изозначением. Некоторое программное обеспечение также позволяет указать электронную плотность в процентах от общего количества включенных электронов. В зависимости от изозначения (типичными единицами измерения являются электроны на кубический бор ) или процента от общего количества включенных электронов, поверхность электронной плотности может использоваться для определения местоположения атомов, подчеркивания электронной плотности, связанной с химическими связями , или для указания общего размера и формы молекулы.

Графически поверхность электронной плотности также служит холстом, на котором могут отображаться другие электронные свойства. Карта электростатического потенциала (свойство электростатического потенциала, отображаемого на электронной плотности) служит индикатором распределения заряда в молекуле. Карта локального потенциала ионизации (свойство локального потенциала ионизации, отображаемое на электронной плотности) является индикатором электрофильности. А карта LUMO ( самая низкая незанятая молекулярная орбиталь, отображаемая на основе электронной плотности) может служить индикатором нуклеофильности.

Определение

Электронная плотность, соответствующая нормированному $N$-электронная волновая функция $\Psi$ (с ${\textbf {r}}$ и $s$ обозначающие пространственную и спиновую переменные соответственно) определяется как

$\rho (\mathbf {r} )=\langle \Psi |{\hat {\rho }}(\mathbf {r} )|\Psi \rangle ,$

где оператор, соответствующий наблюдаемой плотности, равен

${\hat {\rho }}(\mathbf {r} )=\sum _{i=1}^{N}\ \delta (\mathbf {r} -\mathbf {r} _{i}).$

Вычисление $\rho (\mathbf {r} )$ как определено выше, мы можем упростить выражение следующим образом.

${\begin{aligned}\rho (\mathbf {r} )&=\sum _{{s}_{1}}\cdots \sum _{{s}_{N}}\int \ \mathrm {d} \mathbf {r} _{1}\ \cdots \int \ \mathrm {d} \mathbf {r} _{N}\ \left(\sum _{i=1}^{N}\delta (\mathbf {r} -\mathbf {r} _{i})\right)|\Psi (\mathbf {r} _{1},s_{1},\mathbf {r} _{2},s_{2},...,\mathbf {r} _{N},s_{N})|^{2}\\&=N\sum _{{s}_{1}}\cdots \sum _{{s}_{N}}\int \ \mathrm {d} \mathbf {r} _{2}\ \cdots \int \ \mathrm {d} \mathbf {r} _{N}\ |\Psi (\mathbf {r} ,s_{1},\mathbf {r} _{2},s_{2},...,\mathbf {r} _{N},s_{N})|^{2}\end{aligned}}$

Другими словами: удержание одного электрона на месте. ${\textbf {r}}$ мы суммируем по всем возможным расположениям других электронов. Коэффициент N возникает, поскольку все электроны неразличимы, и, следовательно, все интегралы имеют одно и то же значение.

В теориях Хартри-Фока и функционала плотности волновая функция обычно представляется как один определитель Слейтера, построенный из $N$ орбитали, $\varphi _{k}$, с соответствующими профессиями $n_{k}$. В этих ситуациях плотность упрощается до

$\rho (\mathbf {r} )=\sum _{k=1}^{N}n_{k}|\varphi _{k}(\mathbf {r} )|^{2}.$

Общие свойства

По определению, электронная плотность является неотрицательной функцией, интегрирующейся с общим числом электронов. Далее, для системы с кинетической энергией T плотность удовлетворяет неравенствам

${\frac {1}{2}}\int \mathrm {d} \mathbf {r} \ {\big (}\nabla {\sqrt {\rho (\mathbf {r} )}}{\big )}^{2}\leq T.$

${\frac {3}{2}}\left({\frac {\pi }{2}}\right)^{4/3}\left(\int \mathrm {d} \mathbf {r} \ \rho ^{3}(\mathbf {r} )\right)^{1/3}\leq T.$

Для конечных кинетических энергий первое (более сильное) неравенство помещает квадратный корень из плотности в пространство Соболева $H^{1}(\mathbb {R} ^{3})$. Вместе с нормализацией и неотрицательностью это определяет пространство, содержащее физически приемлемые плотности как

${\mathcal {J}}_{N}=\left\{\rho \left|\rho (\mathbf {r} )\geq 0,\ \rho ^{1/2}(\mathbf {r} )\in H^{1}(\mathbf {R} ^{3}),\ \int \mathrm {d} \mathbf {r} \ \rho (\mathbf {r} )=N\right.\right\}.$

Второе неравенство помещает плотность в L ³ космос . Вместе со свойством нормализации размещает приемлемые плотности в пределах пересечения L ¹ и Л ³ - суперсет ${\mathcal {J}}_{N}$.

Топология

Предполагается, что электронная основного состояния плотность атома является монотонно убывающей функцией расстояния от ядра .

Состояние ядерного возврата

Электронная плотность имеет выступы на каждом ядре молекулы из-за неограниченного электрон-ядерного кулоновского потенциала. Это поведение количественно определяется условием возврата Като, сформулированным в терминах сферически усредненной плотности: ${\bar {\rho }}$, относительно любого данного ядра как

$\left.{\frac {\partial }{\partial r_{\alpha }}}{\bar {\rho }}(r_{\alpha })\right|_{r_{\alpha }=0}=-2Z_{\alpha }{\bar {\rho }}(0).$

То есть радиальная производная сферически усредненной плотности, оцененная в любом ядре, равна удвоенной плотности в этом ядре, умноженной на отрицательное значение атомного номера ( $Z$).

поведение

Условие ядерного возврата обеспечивает околоядерное (малое) $r$) поведение плотности как

$\rho (r)\sim e^{-2Z_{\alpha }r}\,.$

Дальняя (большая $r$) известно также поведение плотности, принимающее вид

$\rho (r)\sim e^{-2{\sqrt {2\mathrm {I} }}r}\,.$

где I — энергия ионизации системы.

Плотность ответа

Другое более общее определение плотности - это «плотность линейного отклика». Это плотность, которая при сжатиис любым бесспиновым одноэлектронным оператором получается соответствующее свойство, определяемое как производная энергии. Например, дипольный момент является производной энергии по внешнему магнитному полю и не является математическим ожиданием оператора над волновой функцией. Для некоторых теорий они одинаковы, когда волновая функция сходится. Числа занятости не ограничены диапазоном от нуля до двух, и поэтому иногда даже плотность отклика может быть отрицательной в определенных регионах космоса.

Эксперименты

Многие экспериментальные методы позволяют измерить электронную плотность. Например, квантовая кристаллография посредством рентгеновского дифракционного сканирования, когда рентгеновские лучи подходящей длины волны направляются на образец и измерения проводятся с течением времени, дает вероятностное представление о местоположении электронов. С этих позиций часто можно определить молекулярные структуры, а также точное распределение плотности заряда для кристаллизованных систем. Квантовая электродинамика и некоторые разделы квантовой теории поля также изучают и анализируют суперпозицию электронов и другие связанные явления, такие как индекс NCI , который позволяет изучать нековалентные взаимодействия с использованием электронной плотности. Анализ населения Малликена основан на плотности электронов в молекулах и представляет собой способ разделения плотности между атомами для оценки атомных зарядов.

В просвечивающей электронной микроскопии (ПЭМ) и глубоконеупругом рассеянии , а также в других экспериментах с частицами высоких энергий электроны высокой энергии взаимодействуют с электронным облаком, что дает прямое представление об электронной плотности. ПЭМ, сканирующая туннельная микроскопия (СТМ) и атомно-силовая микроскопия (АСМ) могут использоваться для исследования электронной плотности конкретных отдельных атомов.

Спиновая плотность

Спиновая плотность — это электронная плотность применительно к свободным радикалам . Она определяется как общая электронная плотность электронов одного спина минус полная электронная плотность электронов другого спина. Одним из способов его экспериментального измерения является метод электронного спинового резонанса . нейтронная дифракция позволяет напрямую картировать спиновую плотность в трехмерном пространстве.

См. также

• Карта плотности различий
• Электронное облако
• Электронная конфигурация
• Разрешение (электронная плотность)
• Плотность заряда
• Теория функционала плотности
• Вероятностный ток