Электронная дифракция

Рисунок 1: Дифрактограмма выбранной области двойникового кристалла аустенита в куске стали.

Дифракция электронов — общий термин для явлений, связанных с изменением направления электронных пучков вследствие упругого взаимодействия с атомами . Оно происходит вследствие упругого рассеяния , когда не происходит изменения энергии электронов. Отрицательно заряженные электроны рассеиваются под действием кулоновских сил , когда они взаимодействуют как с положительно заряженным ядром атома, так и с отрицательно заряженными электронами вокруг атомов. Полученная карта направлений электронов вдали от образца называется дифракционной картиной, см., например, рисунок 1 . Помимо рисунков, показывающих направления электронов, дифракция электронов также играет важную роль в контрастности изображений в электронных микроскопах .

В этой статье представлен обзор дифракции электронов и картин дифракции электронов, которые в совокупности называются дифракцией электронов. Сюда входят аспекты того, как в целом электроны могут действовать как волны, дифрагировать и взаимодействовать с материей. Он также включает в себя обширную историю современной дифракции электронов, то, как сочетание разработок 19-го века в области понимания и управления электронами в вакууме и разработок начала 20-го века с использованием электронных волн было объединено с ранними приборами , что привело к появлению электронной микроскопии и дифракции в вакууме. 1920–1935. Хотя это было рождение, с тех пор произошло большое количество дальнейших событий .

Существует множество типов и методов электронной дифракции. Наиболее распространенный подход заключается в том, что электроны проходят через тонкий образец толщиной от 1 до 100 нм (толщина от 10 до 1000 атомов), где результаты зависят от того, как атомы расположены в материале, например, монокристалл , множество кристаллов. или различные типы твердых тел. Другие случаи, такие как более крупные повторы , отсутствие периодичности или беспорядок, имеют свои собственные характерные закономерности. Существует множество различных способов сбора дифракционной информации: от параллельного освещения до сходящегося луча луча электронов или вращения или сканирования по образцу, что дает информацию, которую часто легче интерпретировать. Есть также много других типов инструментов. Например, в сканирующем электронном микроскопе (СЭМ) дифракция обратного рассеяния электронов может использоваться для определения ориентации кристаллов поперек образца. Картины электронной дифракции также можно использовать для характеристики молекул с помощью дифракции электронов в газах , жидкостей и поверхностей с использованием электронов с более низкой энергией. Этот метод называется LEED и метод, называемый RHEED , путем отражения электронов от поверхностей .

Существует также много уровней анализа дифракции электронов, в том числе:

1. Простейшее приближение с использованием длины волны де Бройля для электронов, где только геометрия учитывается и часто закон Брэгга вызывается. Этот подход учитывает только электроны, находящиеся далеко от образца, в дальнем поле или в зоне Фраунгофера. подход.
2. Первый уровень большей точности, при котором предполагается, что электроны рассеиваются только один раз, что называется кинематической дифракцией. а также дальнее поле или Фраунгофера подход.
3. Более полные и точные объяснения, включающие многократное рассеяние, так называемую динамическую дифракцию (например, ссылки ). Они включают более общий анализ с использованием релятивистски скорректированного уравнения Шредингера. методы и отслеживают электроны через образец с точностью как вблизи, так и вдали от образца ( дифракция Френеля и Фраунгофера ).

Дифракция электронов аналогична дифракции рентгеновских лучей и нейтронов . Однако в отличие от дифракции рентгеновских лучей и нейтронов, где простейшие приближения достаточно точны, в дифракции электронов дело обстоит иначе. Простые модели дают геометрию интенсивностей дифракционной картины, но для точных интенсивностей и положения дифракционных пятен необходимы подходы динамической дифракции.

Праймер по дифракции электронов

Всю материю можно представить как волны материи . от мелких частиц, таких как электроны, до макроскопических объектов – хотя невозможно измерить какое-либо «волновое» поведение макроскопических объектов. Волны могут перемещаться вокруг объектов и создавать интерференционные картины. Классическим примером является эксперимент Юнга с двумя щелями, показанный на рисунке 2 , где волна падает на две щели на первом из двух изображений (синие волны). После прохождения щелей есть направления, где волна сильнее, и те, где она слабее – волна дифрагировала . Если вместо двух щелей будет несколько маленьких точек, то может произойти подобное явление, как показано на втором изображении, где волна (красная и синяя) приходит из правого нижнего угла. Это сравнимо с дифракцией электронной волны , где маленькие точки — это атомы в маленьком кристалле, см. также примечание. Обратите внимание на сильную зависимость от взаимной ориентации кристалла и приходящей волны.

Рисунок 2: Эксперимент Янга с двумя щелями: волна показана синим цветом, а две щели — желтым; другой рисунок с красными и синими волнами похож на небольшой массив белых атомов.

Вблизи апертуры или атомов, часто называемых «образцом», электронная волна будет описываться с точки зрения ближнего поля или дифракции Френеля . Это имеет отношение к визуализации в электронных микроскопах . тогда как картины дифракции электронов измеряются вдали от образца, что описывается как дифракция в дальнем поле или дифракция Фраунгофера. Карта направлений электронных волн , покидающих образец, покажет высокую интенсивность (белый цвет) для предпочтительных направлений, таких как три наиболее заметных в двухщелевом эксперименте Юнга на рисунке 2 , в то время как другие направления будут иметь низкую интенсивность (темный цвет). ). Часто бывает множество пятен (предпочтительных направлений), как на рисунке 1 и других рисунках, показанных позже.

История

Историческая справка разделена на несколько подразделов. Первый — это общие сведения об электронах в вакууме и технологические разработки, которые привели к созданию электронно-лучевых трубок, а также электронных трубок , которые доминировали в раннем телевидении и электронике; второй — как это привело к развитию электронных микроскопов; последнее — это работа о природе электронных пучков и основах поведения электронов, ключевом компоненте квантовой механики и объяснении дифракции электронов.

Электроны в вакууме

Смотрите также: Катодный луч и история электрона.

Рисунок 3: Трубка Крукса – без эмиссии (вверху, серый фон) и с эмиссией и тенью из-за мальтийского креста , блокирующего часть электронного луча (внизу, черный фон); см. также электронно-лучевую трубку

Эксперименты с электронными пучками проводились задолго до открытия электрона; Электрон (ἤλεκτρον) — греческое слово, обозначающее янтарь . который связан с записью электростатического заряда Фалесом Милетским около 585 г. до н. э., а возможно, и другими, даже раньше.

В 1650 году Отто фон Герике изобрел вакуумный насос. позволяющий изучать воздействие электричества высокого напряжения, проходящего через разреженный воздух . В 1838 году Майкл Фарадей приложил высокое напряжение между двумя металлическими электродами на обоих концах стеклянной трубки, из которой частично откачали воздух, и заметил странную световую дугу с началом у катода (отрицательный электрод) и концом у анода. (положительный электрод). Опираясь на это, в 1850-х годах Генрих Гейсслер смог добиться давления около 10 ⁻³ атмосферы , изобретая то, что стало известно как трубки Гейсслера . Используя эти трубки, изучая электропроводность в разреженных газах в 1859 году, Юлиус Плюкер заметил, что излучение, испускаемое отрицательно заряженным катодом, вызывает появление фосфоресцирующего света на стенке трубки рядом с ним, и область фосфоресцирующего света можно перемещать, прикладывая магнитного поля.

В 1869 году ученик Плюкера Иоганн Вильгельм Хитторф обнаружил, что твердое тело, помещенное между катодом и фосфоресценцией, отбрасывает тень на стенку трубки, например, рис. 3 . Хитторф пришел к выводу, что катод испускает прямые лучи и что фосфоресценция вызвана лучами, падающими на стенки трубки. В 1876 году Ойген Гольдштейн показал, что лучи испускаются перпендикулярно поверхности катода, что отличает их от света лампы накаливания. Ойген Гольдштейн назвал их катодными лучами . К 1870-м годам Уильям Крукс и другие смогли откачать стеклянные трубки ниже 10 ⁻⁶ атмосфер и заметил, что свечение в трубке исчезало при уменьшении давления, но стекло за анодом начинало светиться. Круксу также удалось показать, что частицы катодных лучей имеют отрицательный заряд и могут отклоняться электромагнитным полем.

В 1897 году Джозеф Томсон измерил массу этих катодных лучей: доказав, что они состоят из частиц. Однако эти частицы были в 1800 раз легче самой лёгкой известной на тот момент частицы — атома водорода . Первоначально они были названы корпускулами назвал их электронами , а позже Джордж Джонстон Стоуни .

Управление электронными лучами, к которому привела эта работа, привело к значительному технологическому прогрессу в электронных усилителях и телевизионных дисплеях.

Волны, дифракция и квантовая механика

См. Также: Введение в квантовую механику и волну материи.

Рисунок 4: Распространение волнового пакета, демонстрирующее движение пучка волн; см . в групповой скорости . более подробную информацию

Независимо от развития электронов в вакууме, примерно в то же время собирались компоненты квантовой механики. В 1924 году Луи де Бройль в своей докторской диссертации «Исследования квантовой теории». представил свою теорию электронных волн. Он предположил, что электрон вокруг ядра можно рассматривать как стоячую волну . и что электроны и всю материю можно рассматривать как волны. Он объединил идею думать о них как о частицах (или корпускулах) и думать о них как о волнах. Он предположил, что частицы — это пучки волн ( волновые пакеты ), которые движутся с групповой скоростью. и иметь эффективную массу , см., например, рисунок 4 . Оба они зависят от энергии, которая, в свою очередь, связана с волновым вектором и релятивистской формулировкой Альберта Эйнштейна, сформулированной несколькими годами ранее.

назвал Это быстро стало частью того, что Эрвин Шредингер волновой механикой . теперь называется уравнением Шрёдингера или волновой механикой. Как заявил Луи де Бройль 8 сентября 1927 года в предисловии к немецкому переводу своих тезисов (в свою очередь переведенному на английский):

М. Эйнштейн с самого начала поддержал мою диссертацию, но именно М. Е. Шредингер разработал уравнения распространения новой теории и в поисках ее решений создал то, что стало известно как «Волновая механика».

Уравнение Шредингера объединяет кинетическую энергию волн и потенциальную энергию, обусловленную для электронов кулоновским потенциалом . Он смог объяснить более ранние работы, такие как квантование энергии электронов вокруг атомов в модели Бора . а также многие другие явления. Электронные волны, как предполагалось де Бройля, автоматически были частью решений его уравнения, см. также введение в квантовую механику и волны материи .

И волновая природа, и подход волновой механики были экспериментально подтверждены для электронных пучков экспериментами двух групп, выполненными независимо: первый - эксперимент Дэвиссона-Гермера , другой - Джорджа Пэджета Томсона и Александра Рида; см. примечание для дальнейшего обсуждения. Александр Рид, аспирант Томсона, провел первые эксперименты. но вскоре он погиб в аварии на мотоцикле и упоминается редко. За этими экспериментами вскоре последовала первая нерелятивистская модель дифракции электронов Ганса Бете. на основе уравнения Шрёдингера, что очень близко к тому, как сейчас описывается дифракция электронов. Примечательно, что Клинтон Дэвиссон и Лестер Гермер заметили что их результаты нельзя интерпретировать с использованием подхода закона Брэгга , поскольку позиции систематически различаются; подход Ганса Бете который учитывает рефракцию из-за среднего потенциала, дал более точные результаты. Эти достижения в понимании механики электронных волн были важны для многих разработок электронных аналитических методов, таких как наблюдения Сейши Кикучи линий, возникающих вследствие комбинированного упругого и неупругого рассеяния, газовая электронография, разработанная Германом Марком и Раймондом Вейлем, дифракция в жидкостях Луи Максвелла, и первые электронные микроскопы, разработанные Максом Ноллом и Эрнстом Руской .

Электронные микроскопы и

Смотрите также: История просвечивающей электронной микроскопии.

Чтобы иметь практичный микроскоп или дифрактометр, недостаточно было просто иметь электронный луч, им нужно было управлять. Многие разработки заложили основу электронной оптики ; обзор ранних работ см. в статье Честера Дж. Калбика. Важным шагом стала работа Генриха Герца в 1883 году. который изготовил электронно-лучевую трубку с электростатическим и магнитным отклонением, продемонстрировав манипуляцию направлением электронного луча. Другие фокусировали электроны осевым магнитным полем Эмилем Вихертом в 1899 году. улучшенные катоды с оксидным покрытием, которые производили больше электронов, Артур Венельт в 1905 году. и разработка электромагнитной линзы в 1926 году Гансом Бушем .

Рисунок 5: Реплика оригинального электронного микроскопа, созданная в 1980 году Эрнстом Руской, в Немецком музее в Мюнхене.

Создание электронного микроскопа предполагает объединение этих элементов, аналогично оптическому микроскопу, но с магнитными или электростатическими линзами вместо стеклянных. По сей день вопрос о том, кто изобрел просвечивающий электронный микроскоп, остается спорным, о чем говорил Томас Малви. и совсем недавно Япин Тао. Обширную дополнительную информацию можно найти в статьях Мартина Фрейндлиха, Рейнхольд Рюденберг и Малви.

Одна попытка была основана на университете. В 1928 году в Берлинском техническом университете Адольф Маттиас (профессор технологии высокого напряжения и электроустановок) назначил Макса Нолля возглавить группу исследователей для продвижения исследований в области электронных лучей и электронно-лучевых осциллографов. В состав команды входили несколько аспирантов, в том числе Эрнст Руска . В 1931 году Макс Нолл и Эрнст Руска успешно создал увеличенные изображения сетчатых сеток, расположенных над анодной апертурой. Устройство, копия которого показана на рисунке 5 , использовало две магнитные линзы для достижения большего увеличения и стало первым электронным микроскопом. (Макс Нолл умер в 1969 году, поэтому не получил доли Нобелевской премии по физике в 1986 году.)

Очевидно, независимой от этих усилий была работа Райнхольда Руденберга в Schuckert Siemens - . Согласно патентному праву (Патент США № 2058914 и 2070318, оба поданы в 1932 году), он является изобретателем электронного микроскопа, но неясно, когда у него появился работающий инструмент. В 1932 году он заявил в очень краткой статье: что Сименс работал над этим несколько лет до того, как в 1932 году были поданы патенты, поэтому его усилия были параллельны усилиям университета. Он умер в 1961 году, столь похожий на Макса Нолла, не имел права на долю Нобелевской премии.

Эти инструменты могли создавать увеличенные изображения, но не были особенно полезны для дифракции электронов; действительно, волновая природа электронов не использовалась во время разработки. Ключом к дифракции электронов в микроскопах стало достижение 1936 года, когда Ганс Бурш показал, что их можно использовать в качестве микродифракционных камер с апертурой. – рождение выделенной области дифракции электронов .

Менее противоречивым было развитие LEED — в ранних экспериментах Дэвиссона и Гермера использовался этот подход. Еще в 1929 году Гермер исследовал адсорбцию газов. а в 1932 году Харрисон Э. Фарнсворт исследовал монокристаллы меди и серебра. Однако доступные в то время вакуумные системы были недостаточно хороши для правильного управления поверхностями, и прошло почти сорок лет, прежде чем они стали доступны. Точно так же только примерно в 1965 году Питер Б. Сьюэлл и М. Коэн продемонстрировали мощь RHEED в системе с очень хорошо контролируемым вакуумом.

разработки в методах

Несмотря на ранние успехи, такие как определение положения атомов водорода в кристаллах NH ₄ Cl В. Е. Лашкаревым и И. Д. Усыкиным в 1933 г., борная кислота Джона М. Коули в 1953 году. и ортоборная кислота Уильяма Хоулдера Захарисена в 1954 году, Дифракция электронов на протяжении многих лет была качественным методом, используемым для проверки образцов в электронных микроскопах. Джон М. Коули объясняет в статье 1968 года:

Так было основано убеждение, в некоторых случаях почти догматическое и сохраняющееся даже по сей день, что невозможно интерпретировать интенсивность картин дифракции электронов для получения структурной информации.

Ситуация изменилась при передаче, отражении и при низких энергиях. Некоторые из ключевых событий (некоторые из которых также описаны позже) с первых дней до 2023 года:

• алгоритме Коули-Муди Быстрые численные методы, основанные на многосрезовом , что стало возможным только когда был разработан метод быстрого преобразования Фурье ( БПФ ). С помощью этих и других численных методов преобразования Фурье выполняются быстро, и стало возможным рассчитывать точную динамическую дифракцию за считанные секунды или минуты на ноутбуках с использованием широко доступных мультисрезовых программ .
• Развитие подхода к дифракции электронов сходящимся пучком . Основываясь на оригинальной работе Вальтера Косселя и Готфрида Мёлленштедта 1939 года, его расширили Питер Гудман и Гюнтер Лемпфуль, затем в основном группами Джона Стидса и Митиёси Танака который показал, как определять точечные группы и пространственные группы . Его также можно использовать для уточнения электронной плотности на более высоком уровне; краткую историю см. в истории CBED . Во многих случаях это лучший метод определения симметрии.
• Разработка новых подходов к уменьшению динамических эффектов, таких как прецессионная электронная дифракция и методы трехмерной дифракции. Эмпирически было обнаружено, что усреднение по различным направлениям значительно снижает эффекты динамической дифракции, например: см . в истории PED дополнительную информацию . С помощью этого подхода не только легче идентифицировать известные структуры, но в некоторых случаях его также можно использовать для решения неизвестных структур. - см. в прецессионной дифракции электронов . дополнительную информацию
• Развитие экспериментальных методов с использованием технологий сверхвысокого вакуума (например, подход, описанный Дэниелом Дж. Альпертом в 1953 году. ) для улучшения поверхностей управления, что делает методы LEED и RHEED более надежными и воспроизводимыми. Вначале поверхности плохо контролировались; с помощью этих технологий их можно очищать и оставаться чистыми в течение нескольких часов или дней, что является ключевым компонентом науки о поверхности .
• Быстрые и точные методы расчета интенсивности для LEED , чтобы их можно было использовать для определения положения атомов, например, эталонов. Они широко использовались для определения структуры многих поверхностей и расположения посторонних атомов на поверхностях.
• Методы моделирования интенсивностей в RHEED , поэтому его можно использовать полуколичественно для понимания поверхностей во время роста и, таким образом, для контроля получаемых материалов.
• Разработка современных детекторов для просвечивающей электронной микроскопии, таких как устройства с зарядовой связью. и детекторы прямых электронов, которые повышают точность и надежность измерений интенсивности. Их эффективность и точность могут быть в тысячу и более раз выше, чем у фотопленки, использовавшейся в самых ранних экспериментах. с информацией, доступной в режиме реального времени, вместо того, чтобы требовать фотографической обработки после эксперимента.

электронов

Плоские волны, волновые векторы

То, что видно на картине дифракции электронов, зависит от образца, а также от энергии электронов. Электроны необходимо рассматривать как волны, что предполагает описание электрона через волновую функцию, записанную в кристаллографических обозначениях (см. примечания и ) как: $$\psi (\mathbf {r} )=\exp(2\pi i\mathbf {k} \cdot \mathbf {r} )$$на должность $\mathbf {r}$. Это описание квантовой механики ; нельзя использовать классический подход. Вектор $\mathbf {k}$ называется волновым вектором, имеет единицы обратных нанометров, а приведенная выше форма называется плоской волной , поскольку член внутри экспоненты постоянен на поверхности плоскости. Вектор $\mathbf {k}$ это то, что используется при рисовании лучевых диаграмм, а в вакууме параллельно направлению или, лучше сказать, групповой скорости или ток вероятности плоской волны. В большинстве случаев электроны движутся со значительной долей скорости света, поэтому их необходимо строго учитывать с помощью релятивистской квантовой механики с помощью уравнения Дирака : которое, поскольку спин обычно не имеет значения, можно свести к уравнению Клейна – Гордона . К счастью, можно обойти многие сложности и использовать нерелятивистский подход, основанный на уравнении Шрёдингера. Вслед за Кунио Фудзивара и Арчибальд Хоуи , Связь между полной энергией электронов и волновым вектором записывается как: $$E={\frac {h^{2}k^{2}}{2m^{*}}}$$с $$m^{*}=m_{0}+{\frac {E}{2c^{2}}}$$где $h$ – постоянная Планка , $m^{*}$ - релятивистская эффективная масса, используемая для компенсации релятивистских членов для электронов с энергией $E$ с $c$ скорость света и $m_{0}$ остальная масса электрона. Понятие эффективной массы встречается во всей физике (см., например, Эшкрофт и Мермин ). и возникает в поведении квазичастиц . Распространенным из них является электронная дырка , которая действует так, как будто это частица с положительным зарядом и массой, аналогичной массе электрона, хотя может быть в несколько раз легче или тяжелее. При дифракции электронов электроны ведут себя так, как если бы они были нерелятивистскими частицами с массой $m^{*}$ с точки зрения того, как они взаимодействуют с атомами.

Длина волны электронов $\lambda$ в вакууме получается из приведенных выше уравнений $$\lambda ={\frac {1}{k}}={\frac {h}{\sqrt {2m^{*}E}}}={\frac {hc}{\sqrt {E(2m_{0}c^{2}+E)}}},$$и может варьироваться от примерно 0,1 нанометра (размер примерно с атом) до тысячной доли этого размера. Обычно энергия электронов выражается в электронвольтах (эВ) — напряжении, используемом для ускорения электронов; Фактическая энергия каждого электрона равна этому напряжению, умноженному на заряд электрона . Для контекста: типичная энергия химической связи составляет несколько эВ; в дифракции электронов участвуют электроны с энергией до 5 000 000 эВ.

Величина взаимодействия электронов с материалом масштабируется как $$2\pi {\frac {m^{*}}{h^{2}k}}=2\pi {\frac {m^{*}\lambda }{h^{2}}}={\frac {\pi }{hc}}{\sqrt {{\frac {2m_{0}c^{2}}{E}}+1}}.$$Хотя волновой вектор увеличивается с увеличением энергии, изменение эффективной массы компенсирует это, поэтому даже при очень высоких энергиях, используемых в дифракции электронов, все еще существуют значительные взаимодействия.

Электроны высокой энергии взаимодействуют с кулоновским потенциалом, что для кристалла можно рассматривать в терминах ряда Фурье (см., например, Эшкрофт и Мермин ), то есть $$V(\mathbf {r} )=\sum V_{g}\exp(2\pi i\mathbf {g} \cdot \mathbf {r} )$$с $\mathbf {g}$ вектор обратной решетки и $V_{g}$ соответствующий коэффициент Фурье потенциала. Вектор обратной решетки часто называют индексами Миллера. $(hkl)$, сумма отдельных векторов обратной решетки $\mathbf {A} ,\mathbf {B} ,\mathbf {C}$ с целыми числами $h,k,l$ в форме: $$\mathbf {g} =h\mathbf {A} +k\mathbf {B} +l\mathbf {C}$$(Иногда векторы обратной решетки записываются как $\mathbf {a} ^{*}$, $\mathbf {b} ^{*}$, $\mathbf {c} ^{*}$ и см. примечание. ) Вклад от $V_{g}$ необходимо объединить с так называемой функцией формы (например, ), что является преобразованием Фурье формы объекта. Если, например, объект мал в одном измерении, то функция формы при преобразовании Фурье простирается далеко в этом направлении — взаимное соотношение.

Рисунок 6: Конструкция сферы Эвальда для дифракции электронов на просвет, показывающая две зоны Лауэ и ошибку возбуждения.

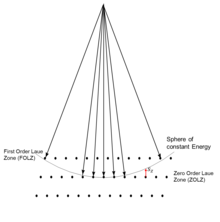
Вокруг каждой точки обратной решетки существует эта функция формы. Насколько интенсивность будет в дифракционной картине, зависит от пересечения сферы Эвальда , то есть сохранения энергии, и функции формы вокруг каждой точки обратной решетки — см. рисунки 6 , 20 и 22 . Вектор от точки обратной решетки к сфере Эвальда называется ошибкой возбуждения. $\mathbf {s} _{g}$.

Для дифракции электронов на пропускание используются тонкие образцы, поэтому большая часть функции формы располагается вдоль направления электронного луча. Для обоих LEED и РИД функция формы в основном перпендикулярна поверхности образца. В LEED это приводит к (упрощенному) обратному отражению электронов, приводящему к образованию пятен, см. рисунки 20 и 21 ниже, тогда как в RHEED электроны отражаются от поверхности под небольшим углом и обычно дают дифракционные картины с полосами, см. рисунок 22. и 23 позже. Для сравнения, как при дифракции рентгеновских лучей, так и при дифракции нейтронов рассеяние значительно слабее, поэтому обычно требуются кристаллы гораздо большего размера, и в этом случае функция формы сжимается примерно до точек обратной решетки, что приводит к более простому закону дифракции Брэгга.

Во всех случаях, когда точки обратной решетки близки к сфере Эвальда (ошибка возбуждения мала), интенсивность имеет тенденцию к увеличению; когда они далеко, он имеет тенденцию быть меньше. Набор дифракционных пятен, расположенных под прямым углом к ​​направлению падающего луча, называется пятнами зоны Лауэ нулевого порядка (ZOLZ), как показано на рисунке 6 . Можно также иметь интенсивности дальше от точек обратной решетки, которые находятся в более высоком слое. Первая из них называется зоной Лауэ первого порядка (FOLZ); серия называется родовым названием зоны Лауэ высшего порядка (HOLZ).

В результате электронная волна после дифракции может быть записана как интеграл по различным плоским волнам: $$\psi (\mathbf {r} )=\int \phi (\mathbf {k} )\exp(2\pi i\mathbf {k} \cdot \mathbf {r} )d^{3}\mathbf {k} ,$$это сумма плоских волн, идущих в разных направлениях, каждая из которых имеет комплексную амплитуду. $\phi (\mathbf {k} )$. (Это трехмерный интеграл, который часто записывают как $d\mathbf {k}$ скорее, чем $d^{3}\mathbf {k}$.) Для кристаллического образца эти волновые векторы должны иметь одинаковую величину для упругого рассеяния (без изменения энергии) и связаны с направлением падения $\mathbf {k} _{0}$ (см. рисунок 6 )

$$\mathbf {k} =\mathbf {k} _{0}+\mathbf {g} +\mathbf {s} _{g}.$$Дифракционная картина определяет интенсивность $$I(\mathbf {k} )=\left|\phi (\mathbf {k} )\right|^{2}.$$Для кристалла они будут находиться вблизи точек обратной решетки, обычно образующих двумерную сетку. Разные образцы и режимы дифракции дают разные результаты, как и разные аппроксимации амплитуд. $\phi (\mathbf {k} )$.

Типичная картина дифракции электронов в ПЭМ и ДМЭ представляет собой сетку пятен высокой интенсивности (белых) на темном фоне, аппроксимирующую проекцию векторов обратной решетки, см. рисунки 1 , 9 , 10 , 11 , 14 и 21 ниже. Существуют также случаи, которые будут упомянуты позже, когда дифракционные картины не являются периодическими , см. рисунок 15 , имеют дополнительную диффузную структуру, как показано на рисунке 16 , или имеют кольца, как на рисунках 12 , 13 и 24 . При коническом освещении, как в CBED, они также могут представлять собой сетку из дисков, см. рисунки 7 , 9 и 18 . RHEED немного другой, см. рисунки 22 , 23 . Если ошибки возбуждения $s_{g}$ были бы равны нулю для каждого вектора обратной решетки, эта сетка находилась бы точно на расстоянии между векторами обратной решетки. Для всех них это было бы эквивалентно условию закона Брэгга. В ПЭМ длина волны мала, и это близко к правильному, но не точному. На практике отклонение позиций от простого закона Брэгга интерпретацией часто пренебрегают, особенно если делается аппроксимация по столбцам (см. ниже).

Кинематическая дифракция

В кинематической теории делается приближение, согласно которому электроны рассеиваются только один раз. Для трансмиссионной дифракции электронов принято предполагать постоянную толщину. $t$, а также так называемая колоночная аппроксимация (например, ссылки и дальнейшее чтение). Для идеального кристалла интенсивность каждого дифракционного пятна $\mathbf {g}$ тогда: $$I_{g}=\left|\phi (\mathbf {k} )\right|^{2}\propto \left|F_{g}{\frac {\sin(\pi ts_{z})}{\pi s_{z}}}\right|^{2}$$где $s_{z}$ - величина ошибки возбуждения $|\mathbf {s} _{z}|$ вдоль z — расстояние вдоль направления луча (условно по оси z) от дифракционного пятна до сферы Эвальда и $F_{g}$ структурный фактор : $$F_{g}=\sum _{j=1}^{N}f_{j}\exp {(2\pi i\mathbf {g} \cdot \mathbf {r} _{j}-T_{j}g^{2})}$$сумма по всем атомам в элементарной ячейке с $f_{j}$ форм-факторы, $\mathbf {g}$ вектор обратной решетки , $T_{j}$ представляет собой упрощенную форму фактора Дебая – Уоллера , и $\mathbf {k}$ - волновой вектор дифракционного луча, который равен: $$\mathbf {k} =\mathbf {k} _{0}+\mathbf {g} +\mathbf {s} _{z}$$для падающего волнового вектора $\mathbf {k} _{0}$, как на рисунке 6 и выше . Ошибка возбуждения проявляется в виде исходящего волнового вектора. $\mathbf {k}$ должен иметь тот же модуль (т.е. энергию), что и входящий волновой вектор $\mathbf {k} _{0}$. Интенсивность дифракции электронов на пропускание колеблется в зависимости от толщины, что может сбивать с толку; аналогичным образом могут быть изменения интенсивности из-за изменений ориентации, а также структурных дефектов, таких как дислокации . Если дифракционное пятно сильное, это может быть связано с тем, что оно имеет больший структурный коэффициент, или потому, что комбинация толщины и ошибки возбуждения является «правильной». Точно так же наблюдаемая интенсивность может быть небольшой, хотя структурный фактор велик. Это может усложнить интерпретацию интенсивностей. Для сравнения, эти эффекты намного меньше при дифракции рентгеновских лучей или дифракции нейтронов , поскольку они гораздо меньше взаимодействуют с веществом и часто подчиняются закону Брэгга. является адекватным.

Эта форма является разумным первым приближением, которое качественно правильно во многих случаях, но для правильного понимания интенсивностей необходимы более точные формы, включая многократное рассеяние (динамическую дифракцию) электронов.

Динамическая дифракция

Хотя кинематическая дифракция достаточна для понимания геометрии дифракционных пятен, она не дает правильного определения интенсивности и имеет ряд других ограничений. Для более полного подхода необходимо включить многократное рассеяние электронов, используя методы, восходящие к ранним работам Ганса Бете в 1928 году. Они основаны на решениях уравнения Шредингера. используя релятивистскую эффективную массу $m^{*}$ описано ранее. Даже при очень высоких энергиях необходима динамическая дифракция, поскольку релятивистская масса и длина волны частично компенсируются, поэтому роль потенциала больше, чем можно было бы подумать.

Рисунок 7: Паттерны CBED с использованием всех электронов, включая только те, которые не потеряли энергию, и те, которые возбудили один или два плазмона.

К основным компонентам современной динамической дифракции электронов относятся:

• Учет рассеяния обратно в падающий луч как от дифрагированных лучей, так и между всеми остальными, а не только однократного рассеяния от падающего луча на дифрагированные. Это важно даже для образцов толщиной всего в несколько атомов.
• Моделируя хотя бы полуэмпирически роль неупругого рассеяния мнимой составляющей потенциала, также называемый «оптическим потенциалом». Всегда имеет место неупругое рассеяние, и часто оно может сильно влиять как на фон, так и иногда на детали, см. рисунки 7 и 18 .
• Численные подходы более высокого порядка для расчета интенсивностей, такие как мультисрез , матричные методы которые называются подходами волн Блоха или подходами кексов . Благодаря этим дифракционным пятнам могут присутствовать отсутствующие в кинематической теории, например
• Вклад в дифракцию от упругой деформации и кристаллографических дефектов , а также то, что Йенс Линдхард назвал струнным потенциалом.
• Для просвечивающих электронных микроскопов эффекты обусловлены изменением толщины образца и нормали к поверхности.
• Как в геометрии рассеяния, так и в расчетах, как для LEED и РИД , эффекты, обусловленные наличием поверхностных ступенек, поверхностных реконструкций и других атомов на поверхности. Часто это существенно меняет детали дифракции.
• Для LEED используйте более тщательный анализ потенциала, поскольку вклад условий обмена может быть важным. Без этого расчеты могут быть недостаточно точными.

Линии Кикучи

Основная статья: Линии Кикучи

Линии Кикучи, впервые наблюдался Сейси Кикучи в 1928 году. представляют собой линейные элементы, созданные электронами, рассеянными как неупруго, так и упруго. При взаимодействии электронного пучка с веществом электроны дифрагируют за счет упругого рассеяния , а также рассеиваются неупруго, теряя часть своей энергии. Они происходят одновременно и не могут быть разделены — согласно копенгагенской интерпретации квантовой механики, можно измерить только вероятности появления электронов на детекторах. Эти электроны образуют линии Кикучи, которые предоставляют информацию об ориентации.

Рисунок 8: Карта Кикучи для гранецентрированного кубического материала внутри стереографического треугольника.

Линии Кикучи идут парами, образуя полосы Кикучи, и индексируются в зависимости от кристаллографических плоскостей, с которыми они связаны, при этом угловая ширина полосы равна величине соответствующего вектора дифракции. $|\mathbf {g} |$. Положение полос Кикучи фиксируется относительно друг друга и ориентации образца, а не против дифракционных пятен или направления падающего электронного пучка. При наклоне кристалла полосы перемещаются по дифракционной картине. Поскольку положение полос Кикучи весьма чувствительно к ориентации кристалла , их можно использовать для точной настройки ориентации оси зоны или определения ориентации кристалла. Их также можно использовать для навигации при изменении ориентации между осями зон, соединенных некоторой полосой, пример такой карты, полученной путем объединения множества локальных наборов экспериментальных паттернов Кикучи, приведен на рисунке 8 ; Карты Кикучи доступны для многих материалов.

Виды и техники

В просвечивающем электронном микроскопе

Рисунок 9: Дифрактограммы (внизу, черный фон) с различной кристалличностью (вверху, диаграммы) и сходимостью пучка. Слева направо: точечная дифракция (параллельное освещение), CBED (сходящаяся) и кольцевая дифракция (параллельно со многими зернами).

Дифракция электронов в ПЭМ использует управляемые электронные пучки с использованием электронной оптики. Различные типы дифракционных экспериментов, например рисунок 9 , предоставляют такую ​​информацию, как константы решетки , симметрии, а иногда и позволяют определить неизвестную кристаллическую структуру .

Обычно его комбинируют с другими методами, например, с изображениями с использованием выбранных дифракционных лучей, изображениями с высоким разрешением. показ атомной структуры, химический анализ с помощью энергодисперсионной рентгеновской спектроскопии , исследования электронной структуры и связей посредством спектроскопии потерь энергии электронов , и исследование электростатического потенциала методом электронной голографии ; этот список не является исчерпывающим. По сравнению с рентгеновской кристаллографией , ПЭМ-анализ значительно более локализован и может использоваться для получения информации от десятков тысяч атомов до нескольких или даже отдельных атомов.

Формирование дифракционной картины

Рисунок 10: Схема изображения магнитной линзы (в центре, диаграмма цветных лучей) с изображением (слева) и дифракционной картиной (справа, черный фон).

В ПЭМ электронный луч проходит через тонкую пленку материала, как показано на рисунке 10 . До и после образца лучом управляет электронная оптика. включая магнитные линзы , дефлекторы и апертуры ; они действуют на электроны подобно тому, как стеклянные линзы фокусируют и контролируют свет. Оптические элементы над образцом используются для управления падающим лучом, который может варьироваться от широкого и параллельного луча до сходящегося конуса и может быть меньше атома - 0,1 нм. При взаимодействии с образцом часть луча дифрагируется, а часть проходит, не меняя своего направления. Это происходит одновременно, поскольку электроны находятся повсюду, пока они не будут обнаружены ( коллапс волновой функции ) согласно Копенгагенской интерпретации .

Под образцом луч контролируется другим набором магнитных магнитов и апертур. Каждый набор изначально параллельных лучей ( плоская волна ) фокусируется первой линзой ( объективом ) в точку в задней фокальной плоскости этой линзы, образуя пятно на детекторе ; карта этих направлений, часто массив пятен, представляет собой дифракционную картину. Альтернативно линзы могут формировать увеличенное изображение образца. Здесь основное внимание уделяется сбору дифракционной картины; дополнительную информацию см. на страницах, посвященных ПЭМ и сканирующей просвечивающей электронной микроскопии .

электронов на

Самый простой метод дифракции в ПЭМ - это дифракция выбранных электронов (SAED), при которой падающий луч широкий и почти параллельный. Апертура используется для выбора конкретной интересующей области, от которой собирается дифракция. Эти отверстия являются частью тонкой фольги из тяжелого металла, такого как вольфрам. в котором есть несколько маленьких отверстий. Таким образом, информация о дифракции может быть ограничена, например, отдельными кристаллитами. К сожалению, метод ограничен сферической аберрацией объектива. это верно только для крупных зерен с десятками тысяч атомов и более; для небольших регионов необходим сфокусированный зонд.

используется параллельный луч Если для получения дифракционной картины от монокристалла , результат аналогичен двумерной проекции обратной решетки кристалла. Отсюда можно определить межплоскостные расстояния и углы, а в некоторых случаях и симметрию кристалла, особенно когда электронный луч направлен вниз по главной оси зоны, см., например, базу данных Жана-Поля Морнироли. Однако аберрации объектива проектора, такие как бочкообразное искажение , а также эффекты динамической дифракции (например, ) нельзя игнорировать. Например, могут появиться определенные дифракционные пятна, которых нет при дифракции рентгеновских лучей. например, из-за условий вымирания Гьоннеса -Муди.

Рисунок 11: Дифракционная картина магния , смоделированная с помощью CrysTBox для различных ориентаций кристаллов. Обратите внимание, как дифракционная картина (белая/черная) меняется в зависимости от ориентации кристалла (желтая).

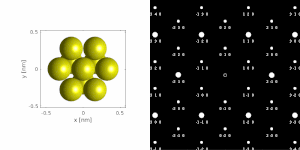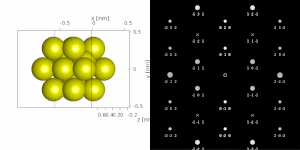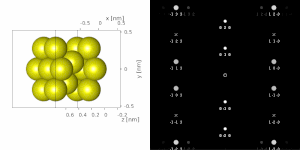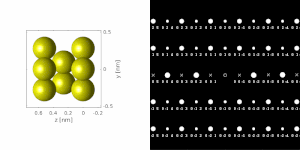
Если образец наклонен относительно электронного луча, в картину вносят вклад разные наборы кристаллографических плоскостей, приводящие к разным типам дифракционных картин, примерно к разным проекциям обратной решетки, см. рисунок 11 . Это можно использовать для определения ориентации кристалла, которую, в свою очередь, можно использовать для установки ориентации, необходимой для конкретного эксперимента. можно получить и обработать серию дифракционных картин, различающихся по наклону Кроме того, с помощью метода дифракционной томографии . Есть способы совместить это с прямых методов с использованием электронов. алгоритмами и другие методы, такие как переворот заряда, или автоматизированная дифракционная томография решать кристаллические структуры.

Поликристаллический узор

Рисунок 12: Связь между точечной и кольцевой дифракцией, проиллюстрированная на от 1 до 1000 зерен MgO с использованием механизма моделирования CrysTBox . Соответствующие экспериментальные схемы можно увидеть на рисунке 13.

Картина дифракции зависит от того, дифрагируется ли луч на одном монокристалле или на нескольких кристаллитах, ориентированных по-разному, например, в поликристаллическом материале. Если присутствует много кристаллитов, дифракционное изображение представляет собой суперпозицию отдельных кристаллических структур, см. рисунок 12 . При большом числе зерен такая суперпозиция дает дифракционные пятна всех возможных векторов обратной решетки. В результате получается узор из концентрических колец, как показано на рисунках 12 и 13 .

Рисунок 13: Кольцевое дифракционное изображение MgO , записанное (слева) и обработанное с помощью RingGUI CrysTBox (справа, с индексацией). Соответствующую смоделированную картину можно увидеть на рисунке 12 .

Текстурированные материалы дают неравномерное распределение интенсивности вокруг кольца, что можно использовать для различения нанокристаллических и аморфных фаз. Однако дифракция часто не может отличить поликристаллические материалы с очень мелкими зернами от аморфных материалов действительно случайного порядка. Здесь просвечивающая электронная микроскопия высокого разрешения и флуктуационная электронная микроскопия может быть более мощным, хотя это все еще тема постоянной разработки.

и

В простых случаях в области, используемой для снятия дифракционной картины, имеется только одно зерно или один тип материала. Однако зачастую их несколько. Если они находятся в разных областях, то картина дифракции будет комбинированной. Кроме того, одно зерно может располагаться поверх другого, и в этом случае электроны, прошедшие через первое, дифрагируют на втором. У электронов нет памяти (как и у многих из нас), поэтому после того, как они прошли через первое зерно и дифрагировали, они пересекают второе, как если бы их текущее направление было направлением падающего луча. Это приводит к появлению дифракционных пятен, которые представляют собой векторную сумму пятен двух (или даже более) обратных решеток кристаллов, и может привести к сложным результатам. Может быть трудно понять, реально ли это и связано ли это с каким-то новым материалом, или это просто случай, когда множественные кристаллы и дифракция приводят к странным результатам.

Объемные и поверхностные надстройки

Многие материалы имеют относительно простые структуры, основанные на векторах небольших элементарных ячеек. $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$ (см. также примечание ). Есть много других, где повторение кратно меньшей элементарной ячейке (субъячейке) в одном или нескольких направлениях, например $N\mathbf {a} ,M\mathbf {b} ,\mathbf {c}$. который имеет большие размеры в двух направлениях. Эти надстройки может возникнуть по многим причинам:

1. Элементарные ячейки большего размера из-за электронного упорядочения, которое приводит к небольшим смещениям атомов в подъячейке. Одним из примеров является упорядочение антисегнетоэлектричества .
2. Химическое упорядочение, то есть разные типы атомов в разных местах субъячейки.
3. Магнитный порядок спинов. На некоторых атомах они могут быть в противоположных направлениях, что приводит к так называемому антиферромагнетизму .

Рис. 14. Дифракция электронов от тонкого образца кремния (111) с восстановленной поверхностью 7х7.

Помимо тех, которые возникают в объеме, сверхструктуры могут возникать и на поверхности. Когда половина материала (номинально) удаляется для создания поверхности, некоторые атомы будут недостаточно скоординированы. Чтобы уменьшить свою энергию, они могут перестроиться. Иногда эти перестановки относительно невелики; иногда они довольно большие. Подобно объемной сверхструктуре, будут дополнительные, более слабые дифракционные пятна. Одним из примеров является поверхность кремния (111), где имеется суперячейка, которая в два направления в семь раз больше простой объемной ячейки. Это приводит к появлению дифракционных картин с дополнительными пятнами, некоторые из которых отмечены на рисунке 14 . Здесь (220) — более сильные объемные дифракционные пятна, а более слабые из-за реконструкции поверхности отмечены 7х7 — см. примечание для комментариев к конвенции.

Апериодические материалы

Рисунок 15: Картина дифракции электронов декагонального квазикристалла.

В апериодическом кристалле структура уже не может быть просто описана тремя разными векторами в реальном или обратном пространстве. В общем случае существует подструктура, описываемая тремя (например, $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$), аналогично суперячейкам, описанным выше, но кроме того есть некоторая дополнительная периодичность (от одного до трех), которую нельзя описать как кратную трем; это настоящая дополнительная периодичность, которая представляет собой иррациональное число относительно решетки субъячеек. Тогда дифракционная картина может быть описана только более чем тремя индексами.

Крайним примером этого являются квазикристаллы . который может быть описан аналогичным образом большим количеством индексов Миллера в обратном пространстве, но не какой-либо трансляционной симметрией в реальном пространстве. Пример этого показан на рисунке 15 для декагонального квазикристалла Al-Cu-Fe-Cr, выращенного методом магнетронного распыления на подложке из хлорида натрия, а затем отделившегося путем растворения подложки водой. В узоре присутствуют пятиугольники, что является признаком апериодической природы этих материалов.

Диффузное рассеяние

Рисунок 16: Один кадр, извлеченный из видео образца Nb _0,83 CoSb, демонстрирующий диффузную интенсивность (змеиную) из-за вакансий в местах Nb.

Дальнейшим шагом за пределами сверхструктур и апериодических материалов является то, что называется диффузным рассеянием на картинах электронной дифракции из-за беспорядка. который также известен как рентгеновский или нейтрон рассеяние. Это может происходить из-за неупругих процессов, например, в объемном кремнии атомные колебания ( фононы ) более преобладают в определенных направлениях, что приводит к появлению полос на дифракционных картинах. Иногда это происходит из-за расположения точечных дефектов . Полностью неупорядоченные точечные дефекты замещения приводят к общему фону, который называется монотонным рассеянием Лауэ. Часто существует распределение вероятностей расстояний между точечными дефектами или типа атома замещения, что приводит к отчетливым трехмерным особенностям интенсивности на дифракционных картинах. Примером этого является образец CoSb Nb _0,83 , дифракционная картина которого показана на рисунке 16 . Из-за вакансий в узлах ниобия возникает диффузная интенсивность со змеевидной структурой, обусловленная корреляцией расстояний между вакансиями, а также релаксацией атомов Co и Sb вокруг этих вакансий.

электронов

Основная статья: Дифракция электронов сходящимся пучком

Рисунок 17: Схема техники CBED. Адаптировано из В. Косселя и Г. Мёлленштедта.

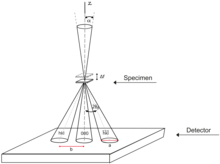
При дифракции электронов сходящимся пучком (CBED) падающие электроны обычно фокусируются в сходящийся пучок конической формы с кроссовером, расположенным на образце, например, рисунок 17 , хотя существуют и другие методы. В отличие от параллельного луча, сходящийся луч способен переносить информацию из объема образца, а не только из двухмерной проекции, доступной в SAED. При использовании сходящегося луча также нет необходимости в апертуре выбранной области, поскольку она по своей сути избирательна по месту, поскольку точка пересечения луча располагается в плоскости объекта, где находится образец.

Рисунок 18: Изменения CBED из-за динамической дифракции с увеличением толщины от a) до d) для Si [110]

Паттерн CBED состоит из дисков, расположенных аналогично пятнам в SAED. Интенсивность внутри дисков отражает динамические дифракционные эффекты и симметрию структуры образца, см. рисунки 7 и 18 . Несмотря на то, что анализ зонной оси и параметров решетки на основе положения дисков существенно не отличается от SAED, анализ содержимого дисков более сложен и часто требуется моделирование, основанное на динамической теории дифракции. Как показано на рисунке 18 , детали внутри диска меняются с толщиной образца, как и неупругий фон. При соответствующем анализе картины CBED можно использовать для индексации точечной группы кристалла, идентификации пространственной группы, измерения параметров решетки, толщины или деформации.

Диаметр диска можно контролировать с помощью оптики и апертуры микроскопа. Чем больше угол, тем шире диски и имеют больше возможностей. Если угол значительно увеличить, диски начинают перекрываться. Этого можно избежать при дифракции сходящегося электронного пучка под большим углом (LACBED), когда образец перемещается вверх или вниз. Однако есть приложения, в которых перекрывающиеся диски полезны, например, в ронхиграмме . Это образец CBED, часто, но не всегда, из аморфного материала, со множеством намеренно перекрывающихся дисков, предоставляющих информацию об оптических аберрациях электронно-оптической системы.

электронов

Основная статья: Прецессионная дифракция электронов

Рисунок 19: Геометрия электронного луча при прецессионной дифракции электронов. Оригинальные дифракционные картины, собранные CS Own в Северо-Западном университете.

Прецессионная дифракция электронов (PED), изобретенная Роджером Винсентом и Полом Мидгли в 1994 году. это метод сбора картин дифракции электронов в просвечивающем электронном микроскопе (ПЭМ). Этот метод включает в себя вращение (прецессию) наклоненного падающего электронного луча вокруг центральной оси микроскопа, компенсируя наклон после образца, так что формируется точечная дифракционная картина, аналогичная картине SAED. Однако диаграмма PED представляет собой интегрирование набора условий дифракции, см. рисунок 19 . Эта интеграция создает квазикинематическую дифракционную картину , которая больше подходит в качестве входных данных в прямых методов с использованием электронов алгоритмы определить кристаллическую структуру образца. Поскольку он позволяет избежать многих динамических эффектов, его также можно использовать для лучшей идентификации кристаллографических фаз.

4D STEM

Основная статья: 4D-сканирующая трансмиссионная электронная микроскопия

4D-сканирующая трансмиссионная электронная микроскопия (4D STEM) представляет собой подмножество методов сканирующей просвечивающей электронной микроскопии (STEM), в которых используется пиксельный детектор электронов для захвата картины дифракции электронов сходящимся пучком (CBED) в каждом месте сканирования; дополнительную информацию смотрите на главной странице. Этот метод захватывает двумерное изображение обратного пространства, связанное с каждой точкой сканирования, в виде растров луча в двухмерной области реального пространства, отсюда и название 4D STEM. Его развитие стало возможным благодаря более совершенным STEM-детекторам и повышению вычислительной мощности. Этот метод находит применение, среди прочего, в дифракционно-контрастной визуализации, фазовой ориентации и идентификации, картировании деформаций и визуализации с атомным разрешением; он стал очень популярным и быстро развивается примерно с 2020 года.

Название 4D STEM часто встречается в литературе, однако оно известно под другими названиями: 4D STEM EELS , ND STEM (N-, поскольку число измерений может быть больше 4), дифракция с позиционным разрешением (PRD), дифрактометрия с пространственным разрешением, импульсная -разрешенная STEM, «прецизионная электронография нанолучей», сканирующая нанодифракция электронов, дифракция электронов нанолучей или пиксельная STEM. Большинство из них одинаковы, хотя есть такие примеры, как STEM с разрешением по импульсу. где акценты могут быть самыми разными.

низкоэнергетических электронов (

Основная статья: Дифракция низкоэнергетических электронов

Рисунок 20: Построение сферы Эвальда для LEED с указанием полос функции формы. $k_{i}$ падающий луч и $k_{f}$ один из дифрагированных лучей.

Рисунок 21: Картина ДМЭ восстановленной поверхности Si(100). Основная решетка представляет собой квадратную решетку, а реконструкция поверхности имеет периодичность 2x1. Также видна электронная пушка, генерирующая первичный электронный луч; он закрывает части экрана.

Дифракция низкоэнергетических электронов (ДМЭ) — метод определения структуры поверхности монокристаллических материалов путем бомбардировки коллимированным пучком электронов низкой энергии (30–200 эВ). В этом случае сфера Эвальда приводит к примерно обратному отражению, как показано на фигуре 20 , и дифрагированным электронам в виде пятен на флуоресцентном экране, как показано на фигуре 21 ; см. главную страницу для получения дополнительной информации и ссылок. С его помощью было решено очень большое количество относительно простых поверхностных структур металлов и полупроводников, а также случаев с простыми хемосорбентами. Для более сложных случаев дифракция трансмиссионных электронов. или поверхностная рентгеновская дифракция часто используются в сочетании со сканирующей туннельной микроскопией и расчетами по теории функционала плотности .

LEED можно использовать одним из двух способов:

1. Качественно, когда регистрируется дифракционная картина и анализ положения пятен дает информацию о симметрии структуры поверхности. В присутствии адсорбата качественный анализ может выявить информацию о размере и ориентации элементарной ячейки адсорбата относительно элементарной ячейки подложки.
2. Количественно, когда интенсивность дифрагированных лучей регистрируется как функция энергии падающего электронного пучка для создания так называемых ВАХ. По сравнению с теоретическими кривыми они могут предоставить точную информацию о положении атомов на поверхности.

Дифракция быстрых электронов на отражение

Основная статья: РИД

Рисунок 22: Сфера Эвальда в_RHEED, где имеют значение зоны Лауэ более высокого порядка.

Рисунок 23: Рисунок RHEED поверхности кремния (111) с реконструкцией 7x7.

Дифракция электронов высоких энергий на отражение (RHEED), это метод , используемый для определения характеристик поверхности кристаллических материалов путем отражения электронов от поверхности. для конструкции сферы Эвальда Как показано на рисунке 22 , она использует в основном зоны Лауэ более высокого порядка, которые имеют компонент отражения. Экспериментальная дифракционная картина показана на рисунке 23 и показывает как кольца из зон Лауэ высшего порядка, так и полосчатые пятна. Системы RHEED собирают информацию только из поверхностных слоев образца, что отличает RHEED от других методов определения характеристик материалов , которые также основаны на дифракции электронов . Просвечивающая электронная микроскопия отбирает в основном большую часть образца, хотя в особых случаях она может предоставить информацию о поверхности. Дифракция низкоэнергетических электронов (LEED) также чувствительна к поверхности и достигает поверхностной чувствительности за счет использования электронов низкой энергии. На сегодняшний день основным применением RHEED является выращивание тонких пленок. поскольку геометрия позволяет одновременно собирать дифракционные данные и наносить. Например, его можно использовать для контроля шероховатости поверхности во время роста, рассматривая как форму полос на дифракционной картине, так и изменения интенсивности.

Газовая электронография

Основная статья: Газовая электронография

Рисунок 24: Газовая электронограмма бензола .

Газовую электронографию можно использовать для определения геометрии молекул (ГЭД ) в газах. Газ, несущий молекулы, подвергается воздействию электронного луча, который дифрагирует на молекулах. Поскольку молекулы ориентированы случайным образом, результирующая дифракционная картина состоит из широких концентрических колец (см. рисунок 24) . Интенсивность дифракции представляет собой сумму нескольких компонентов, таких как фон, атомная интенсивность или молекулярная интенсивность.

В GED интенсивность дифракции под определенным углом дифракции $\theta$ описывается через переменную рассеяния, определяемую как $$|s|={\frac {4\pi }{\lambda }}\sin \left({\frac {\theta }{2}}\right).$$Тогда общая интенсивность выражается как сумма частичных вкладов: $$I_{\text{tot}}(s)=I_{a}(s)+I_{m}(s)+I_{t}(s)+I_{b}(s),$$где $I_{a}(s)$ возникает в результате рассеяния отдельными атомами, $I_{m}(s)$ парами атомов и $I_{t}(s)$ тройками атомов. Интенсивность $I_{b}(s)$ соответствует фону, который, в отличие от предыдущих вкладов, необходимо определять экспериментально. Интенсивность рассеяния атомов $I_{a}(s)$ определяется как $$I_{a}(s)={\frac {K^{2}}{R^{2}}}I_{0}\sum _{i=1}^{N}|f_{i}(s)|^{2},$$где $K=(8\pi ^{2}me^{2})/h^{2}$, $R$ - расстояние между детектором рассеивающего объекта, $I_{0}$ - интенсивность первичного электронного пучка и $f_{i}(s)$ - амплитуда рассеяния атома $i$ молекулярной структуры в эксперименте. $I_{a}(s)$ является основным вкладом и легко получается для известного состава газа. Обратите внимание, что вектор $s$ Используемая здесь ошибка — это не то же самое, что ошибка возбуждения, используемая в других областях дифракции, см. ранее .

Наиболее ценную информацию несет интенсивность молекулярного рассеяния. $I_{a}(s)$, так как содержит информацию о расстоянии между всеми парами атомов в молекуле. Это дано $$I_{m}(s)={\frac {K^{2}}{R^{2}}}I_{0}\sum _{i=1}^{N}\sum _{\stackrel {j=1}{i\neq j}}^{N}\left|f_{i}(s)\right|\left|f_{j}(s)\right|{\frac {\sin[s(r_{ij}-\kappa s^{2})]}{sr_{ij}}}e^{-(1/2l_{ij}s^{2})}\cos[\eta _{i}(s)-\eta _{i}(s)],$$где $r_{ij}$ расстояние между двумя атомами, $l_{ij}$ - среднеквадратическая амплитуда вибрации между двумя атомами, аналогичная фактору Дебая – Уоллера , $\kappa$ – константа ангармонизма и $\eta$ фазовый фактор, который важен для атомных пар с очень разными ядерными зарядами. Суммирование производится по всем парам атомов. Атомный триплет интенсивности $I_{t}(s)$ в большинстве случаев ничтожна. Если молекулярная интенсивность извлекается из экспериментальной картины путем вычитания других вкладов, ее можно использовать для сопоставления и уточнения структурной модели с экспериментальными данными.

Подобные методы анализа также применялись для анализа данных дифракции электронов от жидкостей.

В сканирующем электронном микроскопе

Основная статья: Дифракция обратного рассеяния электронов

Рисунок 25: Линии Кикучи на EBSD-картине кремния .

В сканирующем электронном микроскопе область вблизи поверхности можно нанести на карту с помощью электронного луча, который сканируется по сетке поперек образца. Дифракционная картина может быть записана с помощью дифракции обратного рассеяния электронов (EBSD), как показано на рисунке 25 , снятом камерой внутри микроскопа. Электроны проникают на глубину от нескольких нанометров до нескольких микрон, в зависимости от используемой энергии электронов, некоторые из которых дифрагируют назад и выходят за пределы образца. В результате комбинированного неупругого и упругого рассеяния типичными особенностями EBSD-изображения являются линии Кикучи . Поскольку положение полос Кикучи очень чувствительно к ориентации кристалла, данные EBSD можно использовать для определения ориентации кристалла в определенных местах образца. Данные обрабатываются программным обеспечением, создавая двумерные карты ориентации. Поскольку линии Кикучи несут информацию о межплоскостных углах и расстояниях и, следовательно, о кристаллической структуре, их можно использовать и для фазовой идентификации. или анализ деформации .

Дальнейшее чтение

• Джон М., Коули (1995). Дифракционная физика . Эльзевир. ISBN  0-444-82218-6 . OCLC   247191522 . . Содержит обширный обзор кинематической и других дифракционных явлений.
• Раймер, Людвиг (2013). Просвечивающая электронная микроскопия: физика формирования изображений и микроанализ . Шпрингер Берлин/Гейдельберг. ISBN  978-3-662-13553-2 . OCLC   1066178493 . Большой охват многих различных областей электронной микроскопии с большим количеством ссылок.
• Хирш, ПБ; Хауи, А.; Николсон, РБ; Пэшли, Д.В.; Уилан, MJ (1965). Электронная микроскопия тонких кристаллов . Лондон: Баттервортс. ISBN  0-408-18550-3 . OCLC   2365578 . , часто называемый библией электронной микроскопии.
• Спенс, ЮЧ; Цзо, Дж. М. (1992). Электронная микродифракция . Бостон, Массачусетс: Springer US. дои : 10.1007/978-1-4899-2353-0 . ISBN  978-1-4899-2355-4 . S2CID   45473741 . , большой охват тем, связанных с динамической дифракцией и CBED.
• Пэн, Л.-М.; Дударев С.Л.; Уилан, MJ (2011). Дифракция и микроскопия быстрых электронов . Оксфорд: Издательство Оксфордского университета. ISBN  978-0-19-960224-7 . OCLC   656767858 . . Очень обширное освещение современной динамической дифракции.
• Картер, К. Барри; Уильямс, Дэвид Б.; Томас, Джон М., ред. (2016). Просвечивающая электронная микроскопия: дифракция, визуализация и спектрометрия . Чам, Швейцария: Springer. ISBN  978-3-319-26649-7 . , недавний учебник с множеством изображений, более сильный в экспериментальных аспектах.
• Эдингтон, Джеффри Уильям (1977). Практическая электронная микроскопия в материаловедении . Технические книги. ОСЛК   27997701 . , более старый источник экспериментальных подробностей, хотя его трудно найти.