Линии Кикучи (физика)
Линии Кикучи представляют собой узоры электронов, образующиеся в результате рассеяния. Они объединяются в пары, образуя полосы при дифракции электронов на монокристаллических образцах и служат «дорогами в пространстве ориентации» для микроскопистов, не уверенных в том, на что они смотрят. В просвечивающих электронных микроскопах их легко увидеть при дифракции на участках образца, достаточно толстых для многократного рассеяния. [1] В отличие от дифракционных пятен, которые мигают при наклоне кристалла, полосы Кикучи обозначают пространство ориентации четко определенными пересечениями (называемыми зонами или полюсами), а также путями, соединяющими одно пересечение с другим.
Экспериментальные и теоретические карты геометрии полос Кикучи, а также их аналоги в прямом пространстве, например, контуры изгиба, структуры электронных каналов и карты видимости полос, становятся все более полезными инструментами в электронной микроскопии кристаллических и нанокристаллических материалов. [2] Поскольку каждая линия Кикучи связана с дифракцией Брэгга с одной стороны одного набора плоскостей решетки, эти линии могут быть помечены теми же индексами Миллера или обратной решетки , которые используются для идентификации отдельных дифракционных пятен. Пересечения или зоны полос Кикучи, с другой стороны, индексируются индексами прямой решетки, т.е. индексами, которые представляют собой целые кратные базисных векторов решетки a , b и c .
Линии Кикучи образуются на дифракционных картинах от диффузно рассеянных электронов, например, в результате тепловых колебаний атомов. [3] Основные особенности их геометрии можно вывести из простого упругого механизма, предложенного в 1928 году Сейси Кикучи : [4] динамическая теория диффузного неупругого рассеяния . хотя для их количественного понимания необходима [5]
В рассеянии рентгеновских лучей эти линии называются линиями Косселя. [6] (назван в честь Вальтера Косселя ).
экспериментальных паттернов и Запись карт Кикучи

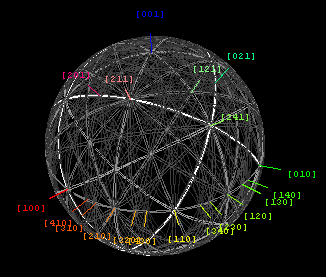
На рисунке слева показаны линии Кикучи, ведущие к кремниевой зоне [100], снятые при направлении луча примерно в 7,9° от зоны вдоль полосы Кикучи (004). Динамический диапазон изображения настолько велик, что только отдельные части пленки не переэкспонированы . За линиями Кикучи гораздо легче следить адаптированными к темноте глазами на флуоресцентном экране, чем запечатлеть неподвижное изображение на бумаге или пленке, даже несмотря на то, что глаза и фотографические носители имеют примерно логарифмическую реакцию на интенсивность освещения. Таким образом, полностью количественная работа над такими особенностями дифракции облегчается большим линейным динамическим диапазоном ПЗС-детекторов . [7]
Это изображение охватывает угловой диапазон более 10° и требует использования камеры меньшей, чем обычно, L. длины Сами ширины полос Кикучи (примерно λL/d , где λ/d примерно вдвое больше угла Брэгга для соответствующей плоскости) значительно меньше 1°, поскольку длина волны λ электронов (в данном случае около 1,97 пикометров) намного меньше, чем длина волны λ электронов (в данном случае около 1,97 пикометров). плоскость решетки сама по себе d-пространство. Для сравнения, d-расстояние для кремния (022) составляет около 192 пикометров, а d-расстояние для кремния (004) составляет около 136 пикометров.
Изображение было получено из области кристалла, толщина которой превышает длину неупругого свободного пробега (около 200 нанометров), поэтому элементы диффузного рассеяния (линии Кикучи) будут более сильными по сравнению с элементами когерентного рассеяния (дифракционные пятна). Тот факт, что сохранившиеся дифракционные пятна выглядят как диски, пересекаемые яркими линиями Кикучи, означает, что дифракционная картина была получена с помощью сходящегося электронного пучка. На практике линии Кикучи легко увидеть в толстых областях либо выбранной области сходящегося пучка , либо на картинах дифракции электронов , но их трудно увидеть при дифракции на кристаллах размером намного меньше 100 нм (где вместо этого становятся важными эффекты видимости полос решетки). Это изображение было записано сходящимся лучом, поскольку это также уменьшает диапазон контрастов, которые необходимо записать на пленку.
Составление карт Кикучи, охватывающих более стерадиана, требует, чтобы было сделано много изображений с наклонами, изменяющимися только постепенно (например, на 2 ° в каждом направлении). Это может быть утомительная работа, но может оказаться полезной при исследовании кристалла с неизвестной структурой, поскольку она может ясно выявить симметрию решетки в трех измерениях. [8]
Линейные карты Кикучи и стереографическая проекция их


На рисунке слева показаны линии Кикучи для большей части ориентационного пространства кремния. Угол между большими зонами [011] и [001] внизу составляет 45° для кремния. Обратите внимание, что четырехкратная зона в правом нижнем углу (здесь обозначена [001]) имеет ту же симметрию и ориентацию, что и зона, обозначенная [100] на экспериментальной схеме выше, хотя эта экспериментальная схема сгибается всего на 10°.
Также обратите внимание, что рисунок слева взят из стереографической проекции с центром в зоне [001]. Такие конформные проекции позволяют отображать части сферической поверхности на плоскость, сохраняя при этом локальные углы пересечения и, следовательно, симметрию зон. Для построения таких карт необходимо уметь рисовать дуги окружностей с очень большим радиусом кривизны. Например, фигура слева была нарисована до появления компьютеров и, следовательно, требовала использования лучевого компаса . Найти лучевой компас сегодня может быть довольно сложно, поскольку гораздо проще рисовать кривые с большим радиусом кривизны (в двух или трех измерениях) с помощью компьютера.
Эффект сохранения угла стереографических графиков еще более очевиден на рисунке справа, который охватывает полные 180 ° ориентационного пространства гранецентрированного или кубического плотноупакованного кристалла, например, такого как золото или алюминий. Анимация следует за {220} полосами видимости границ этого гранецентрированного кубического кристалла между зонами <111>, в этой точке вращение на 60° обеспечивает переход к следующей зоне <111> посредством повторения исходной последовательности. Полосы краевой видимости имеют ту же глобальную геометрию, что и полосы Кикучи, но для тонких образцов их ширина пропорциональна (а не обратно пропорциональна) d-расстоянию. Хотя ширина углового поля (и диапазон наклона), которую экспериментально можно получить с помощью полос Кикучи, обычно намного меньше, анимация предлагает широкоугольное представление о том, как полосы Кикучи помогают информированным кристаллографам находить путь между ориентирами в пространстве ориентации образца монокристалла.
Реальные космические аналоги [ править ]

Линии Кикучи служат для выделения края плоскостей решетки на дифракционных изображениях более толстых образцов. Поскольку углы Брэгга при дифракции электронов высоких энергий очень малы (~ 1/4 градуса для 300 кэВ), полосы Кикучи довольно узки в обратном пространстве. Это также означает, что на изображениях реального космоса плоскости решетки с ребра украшены не элементами диффузного рассеяния, а контрастом, связанным с когерентным рассеянием. Эти особенности когерентного рассеяния включают дополнительную дифракцию (отвечающую за контуры изгиба в изогнутой фольге), большее проникновение электронов (что приводит к появлению паттернов каналирования электронов при сканировании электронных изображений кристаллических поверхностей) и контраст границ решетки (что приводит к зависимости границ решетки интенсивность в зависимости от ориентации луча, которая связана с толщиной образца). Хотя контрастные детали различаются, геометрия следов плоскости решетки этих объектов и карт Кикучи одинакова.
Контуры изгиба и кривые качания [ править ]

Качающиеся кривые [9] (слева) представляют собой графики интенсивности рассеянных электронов в зависимости от угла между падающим электронным пучком и нормалью к набору плоскостей решетки в образце. Поскольку этот угол изменяется в любом направлении, начиная с ребра (при котором электронный луч проходит параллельно плоскостям решетки и перпендикулярно их нормали), луч переходит в состояние дифракции Брэгга, и больше электронов дифрагируются за пределами задней фокальной плоскости апертуры микроскопа. , что приводит к появлению пар (полос) темных линий, видимых на изображении изогнутой кремниевой фольги, показанном на изображении справа.
«Паук» контура изгиба [100] на этом изображении, запертый в области кремния, имеющей форму овального часового стекла размером менее микрометра, был получен с помощью электронов с энергией 300 кэВ. Если наклонить кристалл, паук будет двигаться к краям овала, как будто пытаясь выбраться. Например, на этом изображении пересечение паука [100] сместилось к правой стороне эллипса, поскольку образец был наклонен влево.
Ноги паука и их пересечения могут быть проиндексированы, как показано, точно так же, как и паттерн Кикучи рядом с [100] в разделе об экспериментальных паттернах Кикучи выше. В принципе, можно использовать этот контур изгиба для моделирования векторного наклона фольги (с точностью до миллирадиана ) во всех точках овала.
Карты видимости решетчатых границ [ править ]
Как видно из приведенной выше кривой качания, по мере того, как толщина образца перемещается в диапазон 10 нанометров и меньше (например, для электронов 300 кэВ и межрешеточной решетки около 0,23 нм), угловой диапазон наклонов, который приводит к дифракции и/или полосам решетки контраст становится обратно пропорциональным толщине образца. Таким образом, геометрия видимости полос решетки становится полезной при изучении наноматериалов с помощью электронного микроскопа . [10] [11] точно так же, как контуры изгиба и линии Кикучи полезны при исследовании монокристаллических образцов (например, образцов металлов и полупроводников толщиной в диапазоне десятых микрометров). Приложения к наноструктуре, например, включают: (i) определение параметров трехмерной решетки отдельных наночастиц по изображениям, сделанным под разными углами наклона, [12] (ii) маркировка полос случайно ориентированных коллекций наночастиц, (iii) карты толщины частиц, основанные на изменениях контраста полос под наклоном, (iv) обнаружение икосаэдрических двойников по изображению решетки случайно ориентированных наночастиц и (v) анализ ориентационных взаимосвязей между наночастицами и цилиндрической подложкой.
электронного каналирования Паттерны

Все вышеперечисленные методы включают обнаружение электронов, прошедших через тонкий образец, обычно в просвечивающем электронном микроскопе . С другой стороны, сканирующие электронные микроскопы обычно наблюдают за электронами, «подброшенными вверх», когда сфокусированный электронный луч растрируется по толстому образцу. Паттерны электронного каналирования — это контрастные эффекты, связанные с плоскостями решетки, видимыми с ребра, которые проявляются на изображениях вторичных и / или обратно рассеянных электронов сканирующего электронного микроскопа.
Эффекты контрастности в первом порядке аналогичны эффектам от контуров изгиба, т.е. электроны, которые попадают на кристаллическую поверхность в условиях дифракции, имеют тенденцию к каналированию (проникают глубже в образец без потери энергии) и, таким образом, подбрасывают меньше электронов вблизи входной поверхности для обнаружения. Следовательно, в зависимости от ориентации луча/решетки образуются полосы с уже знакомой геометрией линий Кикучи.
Первое изображение, полученное с помощью сканирующего электронного микроскопа (СЭМ), представляло собой изображение контраста электронных каналов в кремнистой стали . [13] Однако практическое использование этого метода ограничено, поскольку обычно достаточно лишь тонкого слоя абразивного повреждения или аморфного покрытия, чтобы скрыть контраст. [14] Если перед исследованием на образец пришлось нанести проводящее покрытие, чтобы предотвратить заряд, это тоже могло бы скрыть контраст. На расколотых поверхностях и поверхностях, самоорганизующихся в атомном масштабе, структуры каналов электронов, вероятно, найдут все более широкое применение в современных микроскопах в ближайшие годы.
См. также [ править ]
Ссылки [ править ]
- ^ Дэвид Б. Уильямс; К. Барри Картер (1996). Просвечивающая электронная микроскопия: Учебник по материаловедению . Пленум Пресс, Нью-Йорк. ISBN 978-0-306-45324-3 .
- ^ К. Саруватари; Дж. Акаи; Ю. Фукумори; Н. Одзаки; Х. Нагасава; Т. Когуре (2008). «Анализ кристаллической ориентации биоминералов с использованием паттернов Кикучи в ПЭМ» . Дж. Минерал. Бензин. Наука . 103 : 16–22. дои : 10.2465/jmps.070611 .
- ^ Эрл Дж. Киркланд (1998). Передовые вычисления в электронной микроскопии . Пленум Пресс, Нью-Йорк. п. 151. ИСБН 978-0-306-45936-8 .
- ^ С. Кикучи (1928). «Дифракция катодных лучей на слюде». Японский физический журнал . 5 (3061): 83–96. Бибкод : 1928Natur.121.1019N . дои : 10.1038/1211019a0 .
- ^ П. Хирш; А. Хауи; Р. Николсон; Д. У. Пэшли; М.Дж. Уилан (1977). Электронная микроскопия тонких кристаллов . Баттервортс/Кригер, Лондон/Малабар, Флорида. ISBN 978-0-88275-376-8 .
- ^ Р.В. Джеймс (1982). «Глава VIII». Оптические основы дифракции рентгеновских лучей» . Ox Bow Press, Вудбридж, Коннектикут. ISBN 978-0-918024-23-7 .
- ^ JCH Спенс и Дж. Цзо (1992). «Гл. 9». Электронная микродифракция . Пленум, Нью-Йорк. ISBN 978-0-306-44262-9 .
- ^ Э. Левин; У.Л. Белл; Г. Томас (1966). «Дальнейшие применения дифрактограмм Кикучи; карты Кикучи». Журнал прикладной физики . 37 (5): 2141–2148. Бибкод : 1966JAP....37.2141L . дои : 10.1063/1.1708749 .
- ^ Х. Хашимото; А. Хауи; М.Дж. Уилан (1962). «Эффекты аномального поглощения электронов в металлических фольгах: теория и сравнение с экспериментом». Труды Королевского общества А. 269 (1336): 80. Бибкод : 1962RSPSA.269...80H . дои : 10.1098/rspa.1962.0164 . S2CID 97942498 .
- ^ П. Фраундорф; Вэньтао Цинь; П. Моек; Эрик Манделл (2005). «Понимание границ решетки нанокристаллов». Журнал прикладной физики . 98 (11): 114308–114308–10. arXiv : cond-mat/0212281 . Бибкод : 2005JAP....98k4308F . дои : 10.1063/1.2135414 . S2CID 13681236 .
- ^ П. Ван; А.Л. Блелох; У. Фальке; Пи Джей Гудхью (2006). «Геометрические аспекты видимости контраста решетки в нанокристаллических материалах с использованием HAADF STEM». Ультрамикроскопия . 106 (4–5): 277–283. дои : 10.1016/j.ultramic.2005.09.005 .
- ^ Вэньтао Цинь; П. Фраундорф (2003). «Параметры решетки по изображениям прямого космоса при двух наклонах». Ультрамикроскопия . 94 (3–4): 245–262. arXiv : cond-mat/0001139 . дои : 10.1016/S0304-3991(02)00335-2 . ПМИД 12524195 . S2CID 10524417 .
- ^ Нолл М. (1935). «Статический потенциал и вторичная эмиссия тел при электронном облучении». З. Тех. Физ . 11 :467-475.
- ^ Дж. И. Гольдштейн; DE Ньюбери; П. Эхлин; DC Джой; А.Д. Ромиг младший; CE Лайман; К. Фиори; Е. Лифшин (1992). Сканирующая электронная микроскопия и рентгеновский микроанализ . Пленум Пресс, Нью-Йорк. ISBN 978-0-306-44175-2 .
Внешние ссылки [ править ]
- Рассчитывайте шаблоны с помощью WebEMApS в UIUC .
- Несколько интерактивных 3D-карт в UM Saint Louis .
- Рассчитайте карту или шаблоны Кикучи с помощью бесплатного программного обеспечения PTCLab [1] .