Дислокация

Информацию о синтаксической операции см. в разделе «Дислокация (синтаксис)» . Медицинский термин см. в разделе «Вывих сустава» .

Вывихи реберного (слева) и винтового (справа) типа.

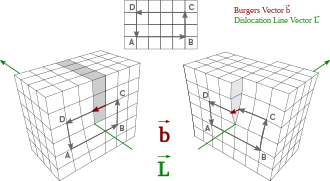
В материаловедении дислокация или или дислокация Тейлора — это линейный кристаллографический дефект неровность внутри кристаллической структуры , которая содержит резкое изменение расположения атомов. Движение дислокаций позволяет атомам скользить друг по другу при низких уровнях напряжения и известно как скольжение или скольжение . Кристаллический порядок восстанавливается по обе стороны от скользящей дислокации , но атомы с одной стороны сместились на одну позицию. Кристаллический порядок не восстанавливается полностью при частичной дислокации . Дислокация определяет границу между скользящими и нескользящими областями материала и в результате должна либо образовать полную петлю, пересечь другие дислокации или дефекты, либо распространиться до краев кристалла. Дислокацию можно охарактеризовать расстоянием и направлением движения, которое она вызывает у атомов, которое определяется вектором Бюргерса . Пластическая деформация материала происходит путем создания и перемещения множества дислокаций. Число и расположение дислокаций влияют на многие свойства материалов .

Двумя основными типами дислокаций являются сидячие дислокации, которые являются неподвижными, и скользящие дислокации, которые являются подвижными. Примерами сидячих дислокаций являются стержнеобразная дислокация и соединение Ломера-Коттрелла . Двумя основными типами подвижных дислокаций являются краевые и винтовые дислокации.

Краевые дислокации можно представить как вызванные обрывом плоскости атомов в середине кристалла . В таком случае окружающие плоскости не являются прямыми, а огибают край конечной плоскости, так что кристаллическая структура идеально упорядочена с обеих сторон. Это явление аналогично тому, как половина листа бумаги вставлена ​​в стопку бумаги, где дефект стопки заметен только у края половины листа.

Теория, описывающая упругие поля дефектов, была первоначально разработана Вито Вольтеррой в 1907 году. В 1934 году Эгон Орован , Майкл Поланьи и Дж. Тейлор предположили, что низкие напряжения, наблюдаемые для возникновения пластической деформации по сравнению с теоретическими предсказаниями того времени, могут быть объяснены. с точки зрения теории дислокаций.

История

Теория, описывающая упругие поля дефектов, была первоначально разработана Вито Вольтеррой в 1907 году. Термин «дислокация», обозначающий дефект атомного масштаба, был введен Дж.И. Тейлором в 1934 году.

До 1930-х годов одной из постоянных задач материаловедения было объяснение пластичности с помощью микроскопа. Упрощенная попытка рассчитать напряжение сдвига , при котором соседние атомные плоскости скользят друг по другу в идеальном кристалле, предполагает, что для материала с модулем сдвига $G$, прочность на сдвиг $\tau _{m}$ примерно определяется:

$\tau _{m}={\frac {G}{2\pi }}.$

Модуль сдвига в металлах обычно находится в диапазоне от 20 000 до 150 000 МПа, что указывает на прогнозируемое напряжение сдвига от 3 000 до 24 000 МПа. Это было трудно совместить с измеренными напряжениями сдвига в диапазоне от 0,5 до 10 МПа.

В 1934 году Эгон Орован , Майкл Поланьи и Дж. Тейлор независимо предположили, что пластическую деформацию можно объяснить с точки зрения теории дислокаций. Дислокации могут двигаться, если атомы одной из окружающих плоскостей разрывают свои связи и вновь соединяются с атомами на конечном крае. По сути, полуплоскость атомов перемещается в ответ на напряжение сдвига, разрывая и реформируя линию связей, по одной (или несколько) за раз. Энергия, необходимая для разрыва ряда связей, гораздо меньше, чем энергия, необходимая для одновременного разрыва всех связей во всей плоскости атомов. Даже эта простая модель силы, необходимой для перемещения дислокации, показывает, что пластичность возможна при гораздо меньших напряжениях, чем в идеальном кристалле. Во многих материалах, особенно пластичных, дислокации являются «носителем» пластической деформации, и энергия, необходимая для их перемещения, меньше энергии, необходимой для разрушения материала.

Механизмы

Дислокация — это линейный кристаллографический дефект или неровность внутри кристаллической структуры, которая содержит резкое изменение расположения атомов. Кристаллический порядок восстанавливается по обе стороны от дислокации, но атомы на одной стороне сместились или соскользнули. Дислокации определяют границу между скользкими и нескользящими областями материала и не могут заканчиваться внутри решетки и должны либо распространяться до свободного края, либо образовывать петлю внутри кристалла. Дислокацию можно охарактеризовать расстоянием и направлением движения, которое она вызывает у атомов в решетке, которое называется вектором Бюргерса. Вектор Бюргерса дислокации остается постоянным, даже если форма дислокации может измениться.

Существует множество типов дислокаций: подвижные дислокации называются скользящими , а неподвижные — сидячими . Движение мобильных дислокаций позволяет атомам скользить друг по другу при низких уровнях напряжения и известно как скольжение или скольжение. Движение дислокаций может быть усилено или затруднено присутствием других элементов внутри кристалла, и со временем эти элементы могут диффундировать к дислокации, образуя атмосферу Коттрелла . Закрепление и отрыв этих элементов в некоторой степени объясняет необычную текучесть стали. Взаимодействие водорода с дислокациями — один из механизмов, предложенных для объяснения водородного охрупчивания .

Дислокации ведут себя так, как будто они представляют собой отдельную сущность внутри кристаллического материала, причем некоторые типы дислокаций могут перемещаться по материалу, сгибаясь, изгибаясь и меняя форму, а также взаимодействуя с другими дислокациями и элементами внутри кристалла. Дислокации возникают в результате деформации кристаллического материала, такого как металлы, что может привести к их возникновению на поверхностях, особенно при концентрациях напряжений или внутри материала на дефектах и ​​границах зерен . Число и расположение дислокаций определяют многие свойства металлов, такие как пластичность , твердость и предел текучести . Термическая обработка , содержание сплава и холодная обработка могут изменить количество и расположение дислокаций, а также то, как они движутся и взаимодействуют, чтобы создать полезные свойства.

Продолжительность: 20 секунд. 0:20

Моделирование дислокаций в алюминии. Показаны только некристаллические атомы.

Генерирование дислокаций

Когда металлы подвергаются холодной обработке (деформация при температурах, относительно низких по сравнению с абсолютной температурой плавления материала, $T_{m}$ т.е. обычно меньше, чем $0.4T_{m}$) плотность дислокаций увеличивается за счет образования новых дислокаций. Последующее увеличение перекрытия полей деформаций соседних дислокаций постепенно увеличивает сопротивление дальнейшему движению дислокаций. Это вызывает упрочнение металла по мере прогрессирования деформации. Этот эффект известен как деформационное упрочнение или деформационное упрочнение.

Плотность дислокаций $\rho$ в материале может быть увеличена пластической деформацией по следующей зависимости:

$\tau \propto {\sqrt {\rho }}$.

Поскольку при пластической деформации плотность дислокаций увеличивается, в материале должен активироваться механизм создания дислокаций. Тремя механизмами образования дислокаций являются гомогенное зарождение, зарождение границ зерен и границы между решеткой и поверхностью, выделения, дисперсные фазы или армирующие волокна.

Гомогенное зародышеобразование

Создание дислокации путем гомогенного зарождения является результатом разрыва атомных связей вдоль линии решетки. Плоскость решетки сдвигается, в результате чего образуются две противоположные полуплоскости или дислокации. Эти дислокации удаляются друг от друга через решетку. Поскольку гомогенное зародышеобразование образует дислокации из совершенных кристаллов и требует одновременного разрыва многих связей, энергия, необходимая для гомогенного зародышеобразования, высока. Например, было показано, что напряжение, необходимое для гомогенного зародышеобразования в меди, равно ${\frac {\tau _{\text{hom}}}{G}}=7.4\times 10^{-2}$, где $G$ – модуль сдвига меди (46 ГПа). Решение для $\tau _{\text{hom}}\,\!$, мы видим, что требуемое напряжение составляет 3,4 ГПа, что очень близко к теоретической прочности кристалла. Следовательно, при обычной деформации гомогенное зародышеобразование требует концентрированного напряжения и очень маловероятно. Зарождение границ зерен и межфазное взаимодействие являются более распространенными источниками дислокаций.

Неровности на границах зерен в материалах могут вызывать дислокации, которые распространяются вглубь зерна. Ступени и выступы на границе зерен являются важным источником дислокаций на ранних стадиях пластической деформации.

Источник Фрэнка-Рида

Основная статья: Источник Фрэнка-Рида

Источник Франка-Рида представляет собой механизм, способный создавать поток дислокаций из закрепленного сегмента дислокации. Напряжение сгибает дислокационный сегмент, расширяясь до тех пор, пока не создаст дислокационную петлю, которая вырвется из источника.

Поверхности

Поверхность кристалла может создавать дислокации в кристалле. Из-за небольших ступенек на поверхности большинства кристаллов напряжение в некоторых участках поверхности значительно превышает среднее напряжение в решетке. Этот стресс приводит к вывихам. Затем дислокации распространяются в решетку таким же образом, как и при зернограничном инициировании. В монокристаллах большая часть дислокаций образуется на поверхности. Было показано, что плотность дислокаций на глубине 200 микрометров в поверхности материала в шесть раз превышает плотность в объеме. Однако в поликристаллических материалах поверхностные источники не оказывают существенного влияния, поскольку большинство зерен не контактируют с поверхностью.

Интерфейсы

Интерфейс между металлом и оксидом может значительно увеличить количество создаваемых дислокаций. Оксидный слой приводит к растяжению поверхности металла, поскольку атомы кислорода сжимаются в решетку, а атомы кислорода сжимаются. Это значительно увеличивает напряжение на поверхности металла и, следовательно, количество образующихся на поверхности дислокаций. Увеличение напряжения на поверхностных ступенях приводит к увеличению количества дислокаций, образующихся и вылетающих из границы раздела.

Дислокации также могут образовываться и оставаться в плоскости границы раздела двух кристаллов. Это происходит, когда период решетки двух кристаллов не совпадает, что приводит к несоответствию решеток на границе раздела. Напряжение, вызванное несоответствием решетки, снимается за счет образования регулярно расположенных дислокаций несоответствия. Дислокации несоответствия — это краевые дислокации с линией дислокации в плоскости интерфейса и вектором Бюргерса в направлении нормали к интерфейсу. Границы раздела с дислокациями несоответствия могут образовываться, например, в результате эпитаксиального роста кристаллов на подложке.

Облучение

Дислокационные петли могут образовываться в результате повреждений, вызванных энергетическим облучением . Призматическая дислокационная петля может пониматься как дополнительный (или отсутствующий) схлопнувшийся диск атомов и может образовываться, когда межузельные атомы или вакансии группируются вместе. Это может произойти непосредственно в результате одного или нескольких каскадов столкновений . что приводит к локально высоким плотностям межузельных атомов и вакансий. В большинстве металлов призматические дислокационные петли являются энергетически наиболее предпочтительными кластерами собственных межузельных атомов.

Взаимодействие и расположение

Геометрически необходимые дислокации

Основная статья: Геометрически необходимые дислокации

Геометрически необходимые дислокации — это расположения дислокаций, которые могут обеспечить ограниченную степень пластического изгиба в кристаллическом материале.Клубки дислокаций обнаруживаются на ранней стадии деформации и проявляются в виде нечетких границ; процесс динамического восстановления приводит в конечном итоге к образованию ячеистой структуры, содержащей границы с разориентировкой менее 15° (малоугловые границы зерен).

Закрепление

Добавление точек закрепления, которые препятствуют движению дислокаций, таких как легирующие элементы, может создать поля напряжений, которые в конечном итоге укрепят материал, поскольку для преодоления напряжения закрепления и продолжения движения дислокаций потребуется более высокое приложенное напряжение.

Эффекты деформационного упрочнения за счет накопления дислокаций и зеренной структуры, образующейся при высоких деформациях, можно устранить соответствующей термообработкой ( отжигом ), способствующей восстановлению и последующей рекристаллизации материала.

Комбинированные технологические приемы наклепа и отжига позволяют контролировать плотность дислокаций, степень переплетения дислокаций и, в конечном итоге, предел текучести материала.

Стойкие полосы скольжения

Основная статья: Стойкие полосы скольжения

Повторное циклирование материала может привести к образованию и группированию дислокаций, окруженных областями, которые относительно свободны от дислокаций. Этот узор образует лестничную структуру, известную как полосы постоянного скольжения (PSB). PSB называются так потому, что они оставляют следы на поверхности металлов, которые, даже будучи удалены полировкой, возвращаются на то же место при продолжительной циклической работе.

Стенки ПСБ состоят преимущественно из краевых дислокаций. Между стенками пластичность передается винтовыми дислокациями.

В местах соприкосновения ПСБ с поверхностью образуются выдавливания и вдавливания, которые при многократном циклическом нагружении могут привести к возникновению усталостной трещины.

Движение

Основные статьи: Скольжение (материаловедение) и ползучесть дислокаций.

Скольжение

Дислокации могут скользить в плоскостях, содержащих как линию дислокации, так и вектор Бюргерса, так называемую плоскость скольжения. Для винтовой дислокации линия дислокации и вектор Бюргерса параллельны, поэтому дислокация может скользить в любой плоскости, содержащей дислокацию. В случае краевой дислокации дислокация и вектор Бюргерса перпендикулярны, поэтому существует одна плоскость, в которой дислокация может скользить.

Восхождение

Подъем дислокации - это альтернативный механизм движения дислокации, который позволяет краевой дислокации выйти из плоскости скольжения. Движущей силой переползания дислокаций является движение вакансий через кристаллическую решетку. Если вакансия перемещается рядом с границей дополнительной полуплоскости атомов, образующей краевую дислокацию, атом в ближайшей к вакансии полуплоскости может перепрыгнуть и заполнить вакансию. Этот сдвиг атомов перемещает вакансию вдоль полуплоскости атомов, вызывая сдвиг или положительный подъем дислокации. Процесс поглощения вакансии на границе полуплоскости атомов, а не ее создания, известен как отрицательное переползание. Поскольку подъем дислокации происходит в результате прыжка отдельных атомов в вакансии, подъем происходит с увеличением диаметра одного атома.

Во время положительного подъема кристалл сжимается в направлении, перпендикулярном дополнительной полуплоскости атомов, поскольку атомы удаляются из полуплоскости. Поскольку отрицательный подъем предполагает добавление атомов в полуплоскость, кристалл растет в направлении, перпендикулярном полуплоскости. Следовательно, сжимающее напряжение в направлении, перпендикулярном полуплоскости, способствует положительному подъему, тогда как растягивающее напряжение способствует отрицательному подъему. Это одно из основных различий между скольжением и подъемом, поскольку скольжение вызывается только напряжением сдвига.

Еще одним отличием между скольжением и переползанием дислокаций является температурная зависимость. Подъем происходит гораздо быстрее при высоких температурах, чем при низких температурах, из-за увеличения движения вакансий. Скольжение, с другой стороны, лишь незначительно зависит от температуры.

Лавины дислокаций

Основная статья: Лавины дислокаций

Лавины дислокаций возникают при многократном одновременном движении дислокаций.

Скорость дислокации

Скорость дислокации во многом зависит от напряжения сдвига и температуры, и ее часто можно определить с помощью степенной функции:

$v=A\tau ^{m}$

где $A$ – материальная константа, $\tau$ – приложенное напряжение сдвига, $m$ – константа, уменьшающаяся с ростом температуры. Увеличение напряжения сдвига приведет к увеличению скорости дислокации, тогда как повышение температуры обычно снижает скорость дислокации. Предполагается, что большее рассеяние фононов при более высоких температурах ответственно за увеличение сил демпфирования, которые замедляют движение дислокаций.

Геометрия

Краевая дислокация (b = вектор Бюргерса )

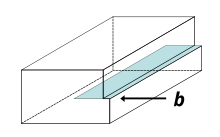
Существуют два основных типа подвижных дислокаций: краевые и винтовые. Дислокации, обнаруженные в реальных материалах, обычно смешанные , то есть обладают характеристиками обоих.

Край

Схематическая диаграмма (плоскости решетки), показывающая краевую дислокацию. Вектор бургеров — черный, линия дислокации — синий.

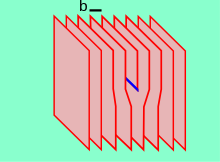
Кристаллический материал состоит из регулярного набора атомов, расположенных в плоскостях решетки. Краевая дислокация — это дефект, при котором в середине кристалла появляется дополнительная полуплоскость атомов, искажающая близлежащие плоскости атомов. Когда с одной стороны кристаллической структуры прикладывается достаточная сила, эта дополнительная плоскость проходит через плоскости атомов, разрывая и соединяя с ними связи, пока не достигнет границы зерна. Дислокация имеет два свойства: направление линии, то есть направление, идущее вдоль нижней части дополнительной полуплоскости, и вектор Бюргерса , который описывает величину и направление искажения решетки. В краевой дислокации вектор Бюргерса перпендикулярен направлению линии.

Напряжения, вызванные краевой дислокацией, сложны из-за присущей ей асимметрии. Эти напряжения описываются тремя уравнениями:

$\sigma _{xx}={\frac {-\mu \mathbf {b} }{2\pi (1-\nu )}}{\frac {y(3x^{2}+y^{2})}{(x^{2}+y^{2})^{2}}}$

$\sigma _{yy}={\frac {\mu \mathbf {b} }{2\pi (1-\nu )}}{\frac {y(x^{2}-y^{2})}{(x^{2}+y^{2})^{2}}}$

$\tau _{xy}={\frac {\mu \mathbf {b} }{2\pi (1-\nu )}}{\frac {x(x^{2}-y^{2})}{(x^{2}+y^{2})^{2}}}$

где $\mu$ – модуль сдвига материала, $\mathbf {b}$ — вектор Бюргерса , $\nu$ - коэффициент Пуассона и $x$ и $y$ являются координатами.

Эти уравнения предполагают наличие вертикально ориентированной гантели напряжений, окружающей дислокацию, со сжатием, испытываемым атомами вблизи «дополнительной» плоскости, и растяжением, испытываемым этими атомами вблизи «недостающей» плоскости.

Винт

Винтовую дислокацию можно визуализировать, разрезав кристалл по плоскости и сдвинув одну половину по другой по вектору решетки, при этом половинки снова соединятся, не оставляя дефекта. Если разрез проходит через кристалл лишь частично, а затем соскользнул, то границей разреза является винтовая дислокация. Он представляет собой структуру, в которой спиральный путь очерчен вокруг линейного дефекта (линии дислокации) атомными плоскостями кристаллической решетки. В чистых винтовых дислокациях вектор Бюргерса параллелен направлению линии. Массив винтовых дислокаций может вызвать так называемую границу скручивания. На границе скручивания рассогласование между соседними кристаллическими зернами происходит из-за совокупного эффекта винтовых дислокаций внутри материала. Эти дислокации вызывают вращательную разориентацию между соседними зернами, что приводит к искривленной деформации вдоль границы. Границы скручивания могут существенно влиять на механические и электрические свойства материалов, влияя на такие явления, как скольжение границ зерен, ползучесть и разрушение. Напряжения, вызванные винтовой дислокацией, менее сложны, чем напряжения краевой дислокации, и требуют только одного уравнения, поскольку симметрия позволяет использовать одну радиальную координату:

$\tau _{r}={\frac {-\mu \mathbf {b} }{2\pi r}}$

где $\mu$ – модуль сдвига материала, $\mathbf {b}$ – вектор Бюргерса, а $r$ является радиальной координатой.Это уравнение предполагает наличие длинного цилиндра напряжения, исходящего наружу от цилиндра и уменьшающегося с расстоянием. Эта простая модель приводит к бесконечному значению ядра дислокации при $r=0$ и поэтому это справедливо только для напряжений за пределами ядра дислокации. Если вектор Бюргерса очень велик, ядро ​​фактически может быть пустым, в результате чего образуется микротрубка , как это обычно наблюдается в карбиде кремния .

Смешанный

Во многих материалах обнаруживаются дислокации, в которых направление линии и вектор Бюргерса не являются ни перпендикулярными, ни параллельными, и эти дислокации называются смешанными дислокациями , имеющими как винтовой, так и краевой характер. Они характеризуются $\varphi$, угол между направлением линии и вектором Бюргерса, где $\varphi =\pi /2$ для чистых краевых дислокаций и $\varphi =0$ при винтовых дислокациях.

Частично

Основная статья: Частичные дислокации

Частичные дислокации оставляют после себя дефект упаковки. Двумя типами частичного вывиха являются частичный вывих Франка , который является сидячим, и частичный вывих Шокли , который является скользящим.

Частичная дислокация Франка образуется путем внедрения или удаления слоя атомов на плоскости {111}, который затем ограничивается частичной дислокацией Франка. Удаление плотноупакованного слоя называется внутренним дефектом упаковки, а вставка слоя называется внешним дефектом упаковки. Вектор Бюргерса нормален к плоскости скольжения {111}, поэтому дислокация не может скользить, а может двигаться только путем набора высоты .

Чтобы снизить общую энергию решетки, краевые и винтовые дислокации обычно диссоциируют в дефект упаковки, ограниченный двумя частичными дислокациями Шокли. Ширина этой области дефекта упаковки пропорциональна энергии дефекта упаковки материала. Комбинированный эффект известен как расширенная дислокация и способен скользить как единое целое. Однако диссоциированные винтовые дислокации должны рекомбинироваться, прежде чем они смогут пересечь скольжение , что затрудняет перемещение этих дислокаций вокруг барьеров. Материалы с низкой энергией дефекта упаковки обладают наибольшей диссоциацией дислокаций и поэтому легче подвергаются холодной обработке.

Лестничный стержень и перекресток

Если две скользящие дислокации, лежащие в разных плоскостях {111}, разделятся на части Шокли и пересекутся, они образуют ступенчатую дислокацию с дислокацией Ломера-Коттрелла на вершине. Его называют лестничным стержнем , потому что он аналогичен стержню, удерживающему ковер на лестнице.

Закон

Геометрические различия между пробежками и изломами

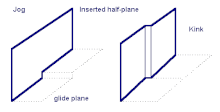
Джог плоскости описывает ступени линии дислокации, которые не находятся в скольжения кристаллической структуры . Линия дислокации редко бывает равномерно прямой, часто содержит множество кривых и ступеней, которые могут препятствовать или облегчать движение дислокации, действуя соответственно как точки или точки зарождения. Поскольку ступеньки находятся вне плоскости скольжения, при сдвиге они не могут двигаться скольжением (движением по плоскости скольжения). Вместо этого им приходится полагаться на то, что диффузия вакансий облегчает передвижение по решетке. Вдали от точки плавления материала диффузия вакансий представляет собой медленный процесс, поэтому для большинства металлов выступы действуют как неподвижные барьеры при комнатной температуре.

Пробки обычно образуются, когда две непараллельные дислокации пересекаются во время скольжения. Наличие выступов в материале повышает его предел текучести за счет предотвращения легкого скольжения дислокаций. Пара неподвижных выступов в дислокации будет действовать как источник Франка-Рида при сдвиге, увеличивая общую плотность дислокаций в материале. Когда предел текучести материала увеличивается за счет увеличения плотности дислокаций, особенно при выполнении механической работы, это называется наклепом . При высоких температурах движение выступов, облегчаемое вакансиями, становится гораздо более быстрым процессом, что снижает их общую эффективность в препятствовании движению дислокаций.

Кинк

Основная статья: Кинк (материаловедение)

Изломы — это ступеньки на линии дислокации, параллельной плоскостям скольжения. В отличие от бега, они облегчают скольжение, действуя как точка зарождения движения дислокаций. Боковое распространение излома от точки зарождения позволяет дислокации распространяться вперед, перемещая только несколько атомов за раз, уменьшая общий энергетический барьер для скольжения.

Пример в двух измерениях (2D)

Диссоциация пары дислокаций вследствие сдвига (красные стрелки) гексагонального кристалла в 2D. Дислокация в 2D состоит из связанной пары пятикратного (зеленый) и семикратного (оранжевый) координационных чисел.

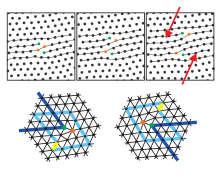
В двух измерениях (2D) существуют только краевые дислокации, которые играют центральную роль в плавлении 2D-кристаллов, но не винтовая дислокация.Эти дислокации являются топологическими точечными дефектами, а это означает, что они не могут быть созданы изолированно путем аффинного преобразования , не разрезая гексагональный кристалл до бесконечности (или, по крайней мере, до его границы). Их можно создавать только в парах с антипараллельным вектором Бюргерса . Если дислокаций много, например. г. при термическом возбуждении дискретный поступательный порядок кристалла разрушается. Одновременно исчезают модуль сдвига и модуль Юнга , что означает, что кристалл расплавлен до жидкой фазы. Ориентационный порядок еще не разрушен (на что указывают линии решетки в одном направлении), и мы обнаруживаем - очень похоже на жидкие кристаллы - жидкую фазу с обычно шестикратным директорным полем. Эта так называемая гексатическая фаза все еще обладает ориентационной жесткостью. Изотропная жидкая фаза возникает, если дислокации диссоциируют на изолированные пяти- и семикратные дисклинации . Это двухступенчатое плавление описывается в рамках так называемой теории Костерлица-Таулесса-Гальперина-Нельсона-Янга ( теория KTHNY ), основанной на двух переходах типа Костерлица-Таулесса .

Наблюдение

Просвечивающая электронная микроскопия (ПЭМ)

Просвечивающая электронная микрофотография дислокаций

Просвечивающая электронная микрофотография дислокаций

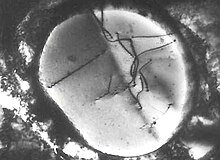
Просвечивающую электронную микроскопию можно использовать для наблюдения дислокаций внутри микроструктуры материала. Готовят тонкую фольгу материала, чтобы сделать ее прозрачной для электронного луча микроскопа. Электронный на регулярных плоскостях кристаллической решетки, образуя дифракционную картину, и в результате луч претерпевает дифракцию этой дифракции (а также за счет изменений толщины, изменения деформации и других механизмов) в изображении создается контраст. Дислокации имеют разную локальную атомную структуру и создают поле деформации, поэтому заставляют электроны в микроскопе рассеиваться по-разному. Обратите внимание на характерный «волнистый» контраст линий дислокаций, когда они проходят через толщу материала на рисунке (дислокации не могут заканчиваться в кристалле, и эти дислокации заканчиваются на поверхностях, поскольку изображение представляет собой двумерную проекцию).

Дислокации не имеют случайной структуры, локальная атомная структура дислокации определяется вектором Бюргерса. Одним из очень полезных применений ПЭМ для визуализации дислокаций является возможность экспериментального определения вектора Бюргерса. Определение вектора Бюргерса достигается так называемым ${\vec {g}}\cdot {\vec {b}}$ («g точка b») анализ. При выполнении темнопольной микроскопии с помощью ПЭМ для формирования изображения выбирается дифрагированное пятно (как упоминалось ранее, плоскости решетки дифрагируют луч на пятна), и изображение формируется с использованием только электронов, которые дифрагировали на плоскости, ответственной за эту дифракцию. место. Вектором на дифракционной картине от прошедшего пятна к дифрагированному пятну является ${\vec {g}}$ вектор. Контраст дислокации масштабируется кратным произведением этого вектора и вектора Бюргерса ( ${\vec {g}}\cdot {\vec {b}}$). В результате, если вектор Бюргерса и ${\vec {g}}$ вектора перпендикулярны, сигнала от дислокации не будет и дислокация вообще не появится на изображении. Следовательно, исследуя различные изображения в темном поле, сформированные из пятен с разными векторами g, можно определить вектор Бюргерса.

Другие методы

Ямки травления, образовавшиеся на концах дислокаций в кремнии, ориентация (111)

Методы полевой ионной микроскопии и атомных зондов предлагают методы получения гораздо большего увеличения (обычно в 3 миллиона раз и выше) и позволяют наблюдать дислокации на атомном уровне. Там, где рельеф поверхности можно разрешить до уровня атомной ступени, винтовые дислокации проявляются как характерные спиральные элементы, что раскрывает важный механизм роста кристаллов: там, где есть поверхностная ступень, атомы могут легче присоединяться к кристаллу, а поверхность ступенька, связанная с винтовой дислокацией, никогда не разрушается, сколько бы атомов к ней ни добавлялось.

Химическое травление

Когда линия дислокации пересекает поверхность металлического материала, связанное с ней поле деформации локально увеличивает относительную восприимчивость материала к кислотному травлению , и в результате образуется ямка травления правильной геометрической формы. Таким образом, дислокации в кремнии, например, можно наблюдать косвенно с помощью интерференционного микроскопа. Ориентацию кристаллов можно определить по форме ямок травления, связанных с дислокациями.

Если материал деформировать и многократно повторно травить, может образоваться серия ямок травления, которые эффективно отслеживают движение рассматриваемой дислокации.

Дислокационные силы

Силы на дислокациях

Движение дислокации в результате внешнего напряжения на кристаллической решетке можно описать с помощью виртуальных внутренних сил, действующих перпендикулярно линии дислокации. Уравнение Пича-Келера может использоваться для расчета силы на единицу длины, действующей на дислокацию, как функции вектора Бюргерса, $\mathbf {b}$стресс, $\sigma$и вектор смысла, $\mathbf {s}$.

$\mathbf {f} =(\mathbf {b} \cdot \sigma )\times \mathbf {s}$

Сила на единицу длины дислокации является функцией общего напряженного состояния: $\mathbf {F}$и вектор смысла, $\mathbf {s}$.

$\mathbf {f} =\mathbf {F} \times \mathbf {s} ={\begin{vmatrix}{\hat {\imath }}&{\hat {\jmath }}&{\hat {k}}\\F_{x}&F_{y}&F_{z}\\s_{x}&s_{y}&s_{z}\end{vmatrix}}$

Компоненты поля напряжений можно получить из вектора Бюргерса, нормальных напряжений, $\sigma$, и касательные напряжения, $\tau$.

${\begin{aligned}F_{x}&=b_{x}\sigma _{xx}+b_{y}\tau _{xy}+b_{z}\tau _{xz}\\F_{y}&=b_{x}\tau _{yx}+b_{y}\sigma _{yy}+b_{z}\tau _{yz}\\F_{z}&=b_{x}\tau _{zx}+b_{y}\tau _{zy}+b_{z}\sigma _{zz}\end{aligned}}$

между

Силу между дислокациями можно получить из энергии взаимодействия дислокаций: $U_{\rm {int}}$. Работа, совершаемая путем смещения граней разреза параллельно выбранной оси, которая создает одну дислокацию в поле напряжений другого смещения. Для $x$ и $y$ направления:

${\begin{aligned}U_{\rm {int}}&=\int _{x}^{\infty }(b_{x}\tau _{xy}+b_{y}\sigma _{yy}+b_{z}\sigma _{zy})\,dx\\U_{\rm {int}}&=\int _{y}^{\infty }(b_{x}\sigma _{xx}+b_{y}\tau _{yx}+b_{z}\sigma _{zx})\,dy\end{aligned}}$

Затем силы находятся путем взятия производных.

${\begin{aligned}F_{x}&=-{\frac {\partial U_{\rm {int}}}{\partial x}}\\F_{y}&=-{\frac {\partial U_{\rm {int}}}{\partial y}}\end{aligned}}$

Свободные поверхностные силы

Дислокации также будут стремиться двигаться к свободным поверхностям из-за более низкой энергии деформации. Эту фиктивную силу можно выразить для винтовой дислокации с $y$ компонент равен нулю как:

$F_{x}=b\tau _{zy}=-{\frac {Gb^{2}}{4\pi d}}$

где $d$ расстояние от свободной поверхности в $x$ направление. Сила, действующая на краевую дислокацию с $y=0$ может быть выражено как:

$F_{x}=b\tau _{xy}=-{\frac {Gb^{2}}{4\pi (1-\nu )d}}$

Внешние ссылки

• Дефекты в кристаллах / Веб-сайт профессора доктора Хельмута Фёлля Глава 5 содержит обширную информацию о дислокациях;
• DoITPoMS Онлайн-учебник по дислокациям, включая фильмы о дислокациях в пузырьковых плотах ;
• Разница между краевой дислокацией и винтовой дислокацией Разница между краевой дислокацией и винтовой дислокацией в деталях;
• Сканирующий туннельный микроскоп – Галерея Галерея изображений, включая страницу дислокаций, наблюдаемых на атомном уровне металлических поверхностей, сделанная группой физики поверхности физического факультета Венского технологического университета, Австрия.
• Вольтерра В. О равновесии многосвязных тел. Пер. от Д. Х. Дельфениха
• Сомильяна, К., «К теории упругих искажений», пер. от Д. Х. Дельфениха