Частичный вывих

Информацию о синтаксической операции см. в разделе «Дислокация (синтаксис)» . Медицинский термин см. в разделе «Вывих сустава» .

В материаловедении частичная дислокация — это разложившаяся форма дислокации , возникающая внутри кристаллического материала. Распространенная дислокация — это дислокация, диссоциировавшая на пару частичных дислокаций. Векторная сумма векторов Бюргерса частичных дислокаций представляет собой вектор Бюргерса расширенной дислокации.

Благоприятность реакции

Дислокация распадется на частичные дислокации, если энергетическое состояние суммы частичных дислокаций меньше энергетического состояния исходной дислокации. Это резюмируется энергетическим критерием Франка :

${\begin{aligned}|{\boldsymbol {b_{1}}}|^{2}>&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (favorable, will decompose)}}\\|{\boldsymbol {b_{1}}}|^{2}<&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (not favorable, will not decompose)}}\\|{\boldsymbol {b_{1}}}|^{2}=&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (will remain in original state)}}\end{aligned}}$

Частичные вывихи Шокли

Частичные дислокации Шокли обычно относятся к паре дислокаций, которые могут привести к наличию дефектов упаковки . Эта пара частичных дислокаций может обеспечить движение дислокации, предоставляя альтернативный путь для движения атомов.

${\begin{aligned}{\boldsymbol {b_{1}}}\rightarrow {\boldsymbol {b_{2}}}+{\boldsymbol {b_{3}}}\end{aligned}}$

В системах FCC примером разложения Шокли является:

${\begin{aligned}{\frac {a}{2}}[10{\overline {1}}]\rightarrow {\frac {a}{6}}[2{\overline {1}}{\overline {1}}]+{\frac {a}{6}}[11{\overline {2}}]\end{aligned}}$

Что энергетически выгодно:

${\begin{aligned}|{\frac {a}{2}}{\sqrt {1^{2}+0^{2}+(-1)^{2}}}|^{2}>&|{\frac {a}{6}}{\sqrt {2^{2}+(-1)^{2}+(-1)^{2}}}|^{2}+|{\frac {a}{6}}{\sqrt {1^{2}+1^{2}+(-2)^{2}}}|^{2}\\{\frac {a^{2}}{2}}>&{\frac {a^{2}}{6}}+{\frac {a^{2}}{6}}\end{aligned}}$

Компоненты частичных частиц Шокли должны составлять исходный вектор, который разлагается:

${\begin{aligned}{\frac {a}{2}}(1)=&{\frac {a}{6}}(2)+{\frac {a}{6}}(1)\\{\frac {a}{2}}(0)=&{\frac {a}{6}}(-1)+{\frac {a}{6}}(1)\\{\frac {a}{2}}(-1)=&{\frac {a}{6}}(-1)+{\frac {a}{6}}(-2)\end{aligned}}$

Откровенные частичные вывихи

Откровенные частичные дислокации сидячие (неподвижные), но могут перемещаться за счет диффузии атомов. В системах FCC части Франка задаются следующим образом:

${\begin{aligned}{\boldsymbol {b}}_{\text{frank}}=&{\frac {a}{3}}[{\text{1 1 1}}]\end{aligned}}$

Тетраэдр Томпсона

Для кристаллов FCC тетраэдры Томпсона или обозначения Томпсона являются изобретенными обозначениями для более простого описания частичных дислокаций. В данной элементарной ячейке отметьте точку A в начале координат, точку B в точке a/2 [110], точку C в точке a/2[011] и точку D в точке a/2[101] — эти точки образуют вершины. тетраэдра. Затем отметьте центры противоположных граней для каждой точки как α, β, γ и δ соответственно. На этом геометрическое представление тетраэдра Томпсона завершено.

Тетраэдр Томпсона, нарисованный внутри кристалла FCC, а затем повернутый, чтобы легче было видеть грани и вершины.

Любая комбинация латинских букв описывает член плоскостей скольжения {111} в кристалле FCC. Вектор, составленный из двух римских букв, описывает вектор Бюргерса идеальной дислокации. Если вектор состоит из латинской буквы и греческой буквы, то это частичный фрагмент Франка, если буквы соответствуют (Aα, Bβ,...), или частичный Шокли в противном случае (Aβ, Aγ,...). Векторы, состоящие из двух греческих букв, описывают дислокации стержня лестницы. Используя нотацию Томпсона, можно добавить векторы Бюргерса для описания других дислокаций и механизмов. Например, две частичные дислокации Шокли можно сложить, чтобы образовать идеальную дислокацию: Aβ + βC = AC. Необходимо, чтобы внутренние буквы данной операции совпадали, но для описания более сложных механизмов можно добавлять их последовательно.

Полезно обобщить эту информацию, используя развернутый тетраэдр Томпсона.

Развернутые тетраэдры Томпсона содержат информацию для быстрого просмотра относительных направлений векторов Бюргерса в структуре FCC.

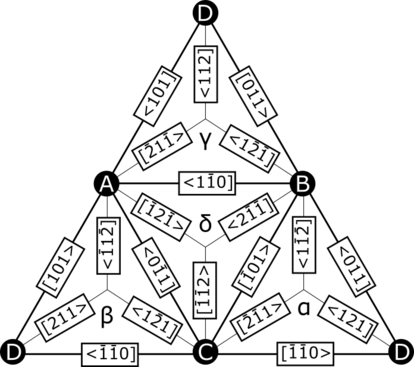
Замок Ломера – Коттрелла

Основная статья: перекресток Ломер-Коттрелл

Дислокация Ломера-Коттрелла образуется в результате более сложной дислокационной реакции. Например, рассмотрим две протяженные дислокации: DB = Dγ + γB и BC = Bδ + δC. При их встрече энергетически выгоднее образовать одиночную дислокацию DC = DB + BC = Dγ + γB + Bδ + δC = Dγ + γδ + δC. Замыкающие частички каждой расширенной дислокации теперь образуют частичку стержня лестницы. Эта структура приводит к уменьшению подвижности дислокаций, поскольку структура ядра неплоская (то есть она не пересекает грань тетраэдра). Такое снижение подвижности превращает дислокацию Ломера-Коттрелла в препятствие для других дислокаций, тем самым упрочняя материал.

Механические последствия

При формировании дефектов упаковки частичные дислокации достигают равновесия, когда энергия отталкивания между частичными дислокациями соответствует энергии притяжения дефекта упаковки. Это означает, что материалы с более высокой энергией дефекта упаковки, т.е. материалы с высоким модулем сдвига и большими векторами Бюргерса, будут иметь меньшее расстояние между частичными дислокациями. И наоборот, материалы с низкой энергией дефекта упаковки будут иметь большие расстояния между частичными дислокациями.

Частичные дислокации движутся свободно, но для того, чтобы перейти в другую плоскость, они должны сначала сжаться, прежде чем перейти в другую плоскость.

Чтобы пересечь скольжение , обе частичные дислокации должны изменить плоскости скольжения. Общий механизм Фриделя-Эскайга требует, чтобы частичные дислокации рекомбинировали в определенной точке перед поперечным скольжением на другую плоскость скольжения. Объединение частей вместе влечет за собой приложение достаточного напряжения сдвига для уменьшения расстояния между ними, поэтому частичные дислокации с низкой энергией дефекта упаковки по своей природе будет труднее соединить вместе и, следовательно, будет труднее преодолеть поперечное скольжение. И наоборот, материалы с высокой энергией дефекта упаковки будут легче подвергаться поперечному скольжению.

Чем легче дислокация может пересекать скольжение, тем свободнее она может обходить препятствия — это затрудняет наклеп. Таким образом, материалы, которые допускают легкое поперечное скольжение (высокая энергия дефекта упаковки), будут подвергаться меньшему наклепу и упрочнению при использовании таких методов, как упрочнение твердым раствором.