Кристаллическая структура

В кристаллографии кристаллическая структура представляет собой описание упорядоченного расположения атомов , ионов или молекул в кристаллическом материале . ^[1] Упорядоченные структуры возникают из-за внутренней природы составляющих частиц и образуют симметричные узоры, которые повторяются вдоль основных направлений трехмерного пространства в материи.

Наименьшая группа частиц в материале, составляющая этот повторяющийся узор, является элементарной ячейкой структуры. Элементарная ячейка полностью отражает симметрию и структуру всего кристалла, которая создается путем повторяющегося перемещения элементарной ячейки вдоль ее главных осей. Векторы трансляции определяют узлы решетки Браве .

Длины главных осей или ребер элементарной ячейки и углы между ними являются постоянными решетки , также называемыми параметрами решетки или параметрами ячейки . кристалла Свойства симметрии описываются понятием пространственных групп . ^[1] Все возможные симметричные расположения частиц в трехмерном пространстве можно описать 230 пространственными группами.

Кристаллическая структура и симметрия играют решающую роль в определении многих физических свойств, таких как расщепление , электронная зонная структура и оптическая прозрачность .

Элементарная ячейка [ править ]

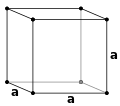
Кристаллическая структура описывается с точки зрения геометрии расположения частиц в элементарных ячейках. Элементарная ячейка определяется как наименьшая повторяющаяся единица, имеющая полную симметрию кристаллической структуры. ^[2] Геометрия элементарной ячейки определяется как параллелепипед с шестью параметрами решетки, принимаемыми как длины ребер ячейки ( a , b , c ) и углы между ними (α, β, γ). Положения частиц внутри элементарной ячейки описываются дробными координатами ( x _i , y _i , z _i ) вдоль краев ячейки, измеренными от контрольной точки. Таким образом, необходимо сообщить только координаты наименьшего асимметричного подмножества частиц, называемого кристаллографической асимметричной единицей. Асимметричную единицу можно выбрать так, чтобы она занимала наименьшее физическое пространство, а это означает, что не все частицы должны физически располагаться внутри границ, заданных параметрами решетки. Все остальные частицы элементарной ячейки порождаются операциями симметрии, характеризующими симметрию элементарной ячейки. Набор операций симметрии элементарной ячейки формально выражается как пространственная группа кристаллической структуры. ^[3]

Простой кубический (П)
Объемноцентрированный куб (I)
Гранецентрированный куб (F)

Индексы Миллера [ править ]

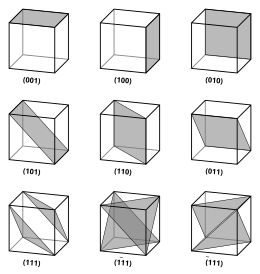
Векторы и плоскости в кристаллической решетке описываются трехзначным индексом Миллера . Этот синтаксис использует индексы h , k и ℓ в качестве параметров направления. ^[4]

По определению синтаксис ( hkℓ ) обозначает плоскость, которая пересекает три точки 1 _/ h , a 2 _/ k и 3 / _a ℓ или их кратное число. То есть индексы Миллера пропорциональны обратным точкам пересечения плоскости с элементарной ячейкой (в базисе векторов решетки). Если один или несколько индексов равны нулю, это означает, что плоскости не пересекают эту ось (т. е. точка пересечения находится «на бесконечности»). Плоскость, содержащая ось координат, переводится так, что она больше не содержит этой оси до определения ее индексов Миллера. Индексы Миллера для плоскости представляют собой целые числа без общих множителей. Отрицательные индексы обозначаются горизонтальными полосами, например (1 2 3). В ортогональной системе координат кубической ячейки индексы Миллера плоскости представляют собой декартовы компоненты вектора, нормального к плоскости.

Учитывая только ( hkℓ ) плоскости, пересекающие одну или несколько точек решетки ( плоскости решетки ), расстояние d между соседними плоскостями решетки связано с (кратчайшим) вектором обратной решетки, ортогональным плоскостям по формуле

d={\frac {2\pi }{|\mathbf {g} _{hk\ell }|}}

Плоскости и направления [ править ]

Кристаллографические направления — это геометрические линии, соединяющие узлы ( атомы , ионы или молекулы ) кристалла. Точно так же кристаллографические плоскости представляют собой геометрические плоскости, соединяющие узлы. Некоторые направления и плоскости имеют более высокую плотность узлов. Эти плоскости высокой плотности влияют на поведение кристалла следующим образом: ^[1]

Оптические свойства : показатель преломления напрямую связан с плотностью (или периодическими колебаниями плотности).
Адсорбция и реакционная способность . Физическая адсорбция и химические реакции происходят на поверхностных атомах или молекулах или вблизи них. Таким образом, эти явления чувствительны к плотности узлов.
Поверхностное натяжение . Конденсация материала означает, что атомы, ионы или молекулы более стабильны, если они окружены другими подобными частицами. Таким образом, поверхностное натяжение границы раздела варьируется в зависимости от плотности на поверхности.

Микроструктурные дефекты : поры и кристаллиты имеют тенденцию иметь прямые границы зерен, соответствующие плоскостям с более высокой плотностью.
Расщепление : обычно происходит преимущественно параллельно плоскостям с более высокой плотностью.
Пластическая деформация : скольжение дислокаций происходит преимущественно параллельно плоскостям с более высокой плотностью. Возмущение, переносимое дислокацией ( вектор Бюргерса ), происходит в плотном направлении. Смещение одного узла в более плотную сторону требует меньшего искажения кристаллической решетки.

Некоторые направления и плоскости определяются симметрией кристаллической системы. В моноклинных, тригональных, тетрагональных и гексагональных системах есть одна уникальная ось (иногда называемая главной осью ), которая имеет более высокую вращательную симметрию , чем две другие оси. Базисной плоскостью называется плоскость, перпендикулярная главной оси в этих кристаллических системах. Для триклинных, орторомбических и кубических кристаллических систем обозначение оси произвольное и главная ось отсутствует.

Кубические структуры [ править ]

В частном случае простых кубических кристаллов векторы решетки ортогональны и имеют одинаковую длину (обычно обозначаются a ); аналогично для обратной решетки. Итак, в этом общем случае индексы Миллера ( ℓmn ) и [ ℓmn ] просто обозначают нормали/направления в декартовых координатах . Для кубических кристаллов с постоянной решетки a расстояние d между соседними (ℓmn) плоскостями решетки составляет (сверху):

d_{\ell mn}={\frac {a}{\sqrt {\ell ^{2}+m^{2}+n^{2}}}}

Из-за симметрии кубических кристаллов можно менять место и знак целых чисел и иметь эквивалентные направления и плоскости:

Координаты в угловых скобках, например ⟨100⟩, обозначают семейство направлений, которые эквивалентны благодаря операциям симметрии, например [100], [010], [001] или отрицательному значению любого из этих направлений.
Координаты в фигурных скобках или фигурных скобках, таких как {100}, обозначают семейство нормалей плоскости, которые эквивалентны благодаря операциям симметрии, подобно тому, как угловые скобки обозначают семейство направлений.

Для гранецентрированных кубических (ГЦК) и объемноцентрированных кубических (ОЦК) решеток примитивные векторы решетки не ортогональны. Однако в этих случаях индексы Миллера традиционно определяются относительно векторов решетки кубической суперячейки и, следовательно, снова являются просто декартовыми направлениями .

Межплоскостное расстояние [ править ]

Расстояние d между соседними ( hkℓ ) плоскостями решетки определяется выражением: ^[5]^[6]

Кубический:
${\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}+\ell ^{2}}{a^{2}}}$
Четырехугольный:
${\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}}{a^{2}}}+{\frac {\ell ^{2}}{c^{2}}}$
Шестиугольный:
${\frac {1}{d^{2}}}={\frac {4}{3}}\left({\frac {h^{2}+hk+k^{2}}{a^{2}}}\right)+{\frac {\ell ^{2}}{c^{2}}}$
Ромбоэдрическая ( примитивная постановка ):
${\frac {1}{d^{2}}}={\frac {(h^{2}+k^{2}+\ell ^{2})\sin ^{2}\alpha +2(hk+k\ell +h\ell )(\cos ^{2}\alpha -\cos \alpha )}{a^{2}(1-3\cos ^{2}\alpha +2\cos ^{3}\alpha )}}$
Орторомбический:
${\frac {1}{d^{2}}}={\frac {h^{2}}{a^{2}}}+{\frac {k^{2}}{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}$
Моноклиника:
${\frac {1}{d^{2}}}=\left({\frac {h^{2}}{a^{2}}}+{\frac {k^{2}\sin ^{2}\beta }{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}-{\frac {2h\ell \cos \beta }{ac}}\right)\csc ^{2}\beta$
Триклиника:
${\frac {1}{d^{2}}}={\frac {{\frac {h^{2}}{a^{2}}}\sin ^{2}\alpha +{\frac {k^{2}}{b^{2}}}\sin ^{2}\beta +{\frac {\ell ^{2}}{c^{2}}}\sin ^{2}\gamma +{\frac {2k\ell }{bc}}(\cos \beta \cos \gamma -\cos \alpha )+{\frac {2h\ell }{ac}}(\cos \gamma \cos \alpha -\cos \beta )+{\frac {2hk}{ab}}(\cos \alpha \cos \beta -\cos \gamma )}{1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}$

Классификация по симметрии [ править ]

Определяющим свойством кристалла является присущая ему симметрия. Выполнение определенных операций симметрии над кристаллической решеткой оставляет ее неизменной. Все кристаллы обладают трансляционной симметрией в трех направлениях, но некоторые имеют и другие элементы симметрии. Например, поворот кристалла на 180 ° вокруг определенной оси может привести к образованию атомной конфигурации, идентичной исходной конфигурации; кристалл обладает двойной вращательной симметрией относительно этой оси. Помимо вращательной симметрии, кристалл может обладать симметрией в виде зеркальных плоскостей, а также так называемыми компаунд-симметриями, представляющими собой комбинацию трансляционной и вращательной или зеркальной симметрии. Полная классификация кристалла достигается тогда, когда идентифицированы все присущие кристаллу симметрии. ^[7]

Решётчатые системы [ править ]

Решеточные системы представляют собой группировку кристаллических структур по точечным группам их решетки. Все кристаллы попадают в одну из семи систем решеток. Они связаны с семью кристаллическими системами , но не тождественны им .

Обзор распространенных решетчатых систем
Кристальная семья	Решетчатая система	Группа точек ( обозначение Шёнфлиса )	14 решеток Браве
Кристальная семья	Решетчатая система	Группа точек ( обозначение Шёнфлиса )	Примитивный (P)	По центру основания (S)	Телоцентрированное (I)	По центру лица (F)
Триклиника (а)		C_Там	АП
Моноклиника (м)		С _{2 часа}	член парламента	РС
Орторомбический (о)		Д _{2 часа}	на	ты	привет	из
Четырехугольный (т)		Д _{4 часа}	ТП		из
Шестиугольный (h)	Ромбоэдрический	Д _3д	HR
Шестиугольный (h)	Шестиугольный	Д _6ч	л.с.
Кубический (с)		Ой	КП		Там	CF

Наиболее симметричная, кубическая или изометрическая система, имеет симметрию куба , то есть имеет четыре оси вращения тройного порядка, ориентированные под углом 109,5° ( тетраэдрический угол ) по отношению друг к другу. Эти тройные оси лежат вдоль диагоналей тела куба. Остальные шесть систем решетки — гексагональная , тетрагональная , ромбоэдрическая (часто путаемая с тригональной кристаллической системой ), орторомбическая , моноклинная и триклинная .

Решетки Браве [ править ]

Решетки Браве , также называемые пространственными решетками , описывают геометрическое расположение точек решетки. ^[4] и, следовательно, трансляционная симметрия кристалла. Три измерения пространства образуют 14 различных решеток Браве, описывающих трансляционную симметрию. Все признанные сегодня кристаллические материалы, за исключением квазикристаллов , соответствуют одному из этих механизмов. Четырнадцать трехмерных решеток, классифицированных по системе решеток, показаны выше.

Кристаллическая структура состоит из одной и той же группы атомов, основы , расположенной вокруг каждой точки решетки. Таким образом, эта группа атомов повторяется бесконечно в трех измерениях в соответствии с расположением одной из решеток Браве. Характерная вращательная и зеркальная симметрия элементарной ячейки описывается ее кристаллографической точечной группой .

Кристаллические системы [ править ]

Кристаллическая система — это совокупность точечных групп, в которой сами точечные группы и соответствующие им пространственные группы отнесены к решеточной системе. Из 32 точечных групп, существующих в трех измерениях, большинство отнесено только к одной системе решетки, и в этом случае кристаллическая система и система решетки имеют одно и то же имя. Однако пять точечных групп относятся к двум системам решетки, ромбоэдрической и гексагональной, поскольку обе системы решетки обладают тройной вращательной симметрией. Эти точечные группы отнесены к тригональной кристаллической системе.

Обзор кристаллических систем
Кристальная семья	Кристаллическая система	Группа точек /Класс кристаллов	Шенфлис	Симметрия точек	Заказ	Абстрактная группа
триклиника		педаль	С ₁	энантиоморфный полярный	1	тривиальный $\mathbb {Z} _{1}$
триклиника		пинакоидальный	С _я (S ₂ )	центросимметричный	2	циклический $\mathbb {Z} _{2}$
моноклинический		клиновидный	С ₂	энантиоморфный полярный	2	циклический $\mathbb {Z} _{2}$
		домашний	С _с (С _1h )	полярный	2	циклический $\mathbb {Z} _{2}$
		призматический	С _{2 часа}	центросимметричный	4	Кляйн четыре $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
орторомбический		ромбически-дисфеноидальный	D ₂ (V)	энантиоморфный	4	Кляйн четыре $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
		ромбически- пирамидальный	С _{2 в}	полярный	4	Кляйн четыре $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
		ромбически- дипирамидальный	Д _2ч (В _ч )	центросимметричный	8	$\mathbb {V} \times \mathbb {Z} _{2}$
четырехугольный		тетрагонально-пирамидальный	С ₄	энантиоморфный полярный	4	циклический $\mathbb {Z} _{4}$
		тетрагонально-дисфеноидальный	С ₄	нецентросимметричный	4	циклический $\mathbb {Z} _{4}$
		тетрагонально-дипирамидальный	С _{4 часа}	центросимметричный	8	$\mathbb {Z} _{4}\times \mathbb {Z} _{2}$
		тетрагонально-трапецоэдрический	Д ₄	энантиоморфный	8	двугранный $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		дитетрагонально-пирамидальный	С _4В	полярный	8	двугранный $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		тетрагонально-скаленоэдрический	Д _2д (В _д )	нецентросимметричный	8	двугранный $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		дитетрагонально-дипирамидальный	Д _{4 часа}	центросимметричный	16	$\mathbb {D} _{8}\times \mathbb {Z} _{2}$
шестиугольный	тригональный	тригонально-пирамидальный	С ₃	энантиоморфный полярный	3	циклический $\mathbb {Z} _{3}$
		ромбоэдрический	С _3и (С ₆ )	центросимметричный	6	циклический $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		тригонально-трапецоэдрический	Д ₃	энантиоморфный	6	двугранный $\mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}$
		дитригонально-пирамидальный	С _3В	полярный	6	двугранный $\mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}$
		дитригонально-скаленоэдрический	Д _3д	центросимметричный	12	двугранный $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
	шестиугольный	шестиугольно-пирамидальный	C_С6	энантиоморфный полярный	6	циклический $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		тригонально-дипирамидальный	С _{3 часа}	нецентросимметричный	6	циклический $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		шестиугольно-дипирамидальный	С _{6 часов}	центросимметричный	12	$\mathbb {Z} _{6}\times \mathbb {Z} _{2}$
		шестиугольно-трапецоэдрический	Д ₆	энантиоморфный	12	двугранный $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		дигексагонально-пирамидальный	С _6в	полярный	12	двугранный $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		дитригонально-дипирамидальный	Д _{3 часа}	нецентросимметричный	12	двугранный $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		дигексагонально-дипирамидальный	Д _6ч	центросимметричный	24	$\mathbb {D} _{12}\times \mathbb {Z} _{2}$
кубический		тетартоидный	Т	энантиоморфный	12	чередование $\mathbb {A} _{4}$
		диплоидный	Т _ч	центросимметричный	24	$\mathbb {A} _{4}\times \mathbb {Z} _{2}$
		гироидальный	ТО	энантиоморфный	24	симметричный $\mathbb {S} _{4}$
		шестигранный	Т _д	нецентросимметричный	24	симметричный $\mathbb {S} _{4}$
		шестиоктаэдрический	Ой	центросимметричный	48	$\mathbb {S} _{4}\times \mathbb {Z} _{2}$

Всего существует семь кристаллических систем: триклинная, моноклинная, ромбическая, тетрагональная, тригональная, гексагональная и кубическая.

Группы точек [ править ]

Кристаллографическая точечная группа или класс кристаллов — это математическая группа, включающая операции симметрии, которые оставляют по крайней мере одну точку неподвижной и оставляют неизменным внешний вид кристаллической структуры. Эти операции симметрии включают в себя

Reflection , который отражает структуру через плоскость отражения.
Rotation , который поворачивает структуру на определенную часть круга вокруг оси вращения.
Инверсия , которая меняет знак координаты каждой точки относительно центра симметрии или точки инверсии.
Неправильное вращение , которое состоит из вращения вокруг оси с последующей инверсией.

Оси вращения (собственные и неправильные), плоскости отражения и центры симметрии вместе называются элементами симметрии . Существует 32 возможных класса кристаллов. Каждый из них может быть отнесен к одной из семи кристаллических систем.

Пространственные группы [ править ]

Помимо операций точечной группы, пространственная группа кристаллической структуры содержит операции трансляционной симметрии. К ним относятся:

Чистые трансляции , которые перемещают точку по вектору.
Винтовые оси , которые вращают точку вокруг оси, перемещаясь параллельно оси. ^[8]
Скользящие плоскости , которые отражают точку через плоскость, перемещая ее параллельно плоскости. ^[8]

Существует 230 различных пространственных групп.

координация Атомная

Рассматривая расположение атомов относительно друг друга, их координационные числа, межатомные расстояния, типы связей и т. д., можно составить общее представление о структурах и альтернативных способах их визуализации. ^[9]

Плотная упаковка [ править ]

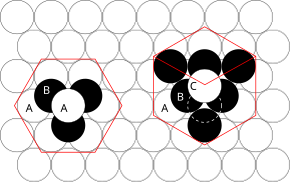
Принципы, связанные с этим, можно понять, рассмотрев наиболее эффективный способ упаковки сфер одинакового размера и укладки плотноупакованных атомных плоскостей в трех измерениях. Например, если плоскость A лежит под плоскостью B, существует два возможных способа размещения дополнительного атома поверх слоя B. Если бы дополнительный слой был помещен непосредственно над плоскостью A, это привело бы к следующей серии:

... АБАБАБАБ ...

Такое расположение атомов в кристаллической структуре известно как плотная гексагональная упаковка (ГПУ) .

Однако если все три плоскости расположены в шахматном порядке друг относительно друга и только после того, как четвертый слой будет расположен непосредственно над плоскостью А, последовательность повторится, то возникает следующая последовательность:

... ABCABCABC ...

Этот тип структурного расположения известен как плотная кубическая упаковка (ККТ) .

Элементарной ячейкой расположения атомов CCP является гранецентрированная кубическая (ГЦК) элементарная ячейка. Это не сразу очевидно, поскольку плотноупакованные слои параллельны плоскостям {111} ГЦК-элементарной ячейки. Существует четыре различных ориентации плотноупакованных слоев.

НПФ и CN [ править ]

Одной из важных характеристик кристаллической структуры является фактор упаковки атомов (APF). Это рассчитывается в предположении, что все атомы представляют собой одинаковые сферы с достаточно большим радиусом, чтобы каждая сфера упиралась в следующую. Фактор упаковки атомов представляет собой долю пространства, заполненную этими сферами, которую можно определить, вычислив общий объем сфер и разделив его на объем ячейки следующим образом:

\mathrm {APF} ={\frac {N_{\mathrm {particle} }V_{\mathrm {particle} }}{V_{\text{unit cell}}}}

Другой важной характеристикой кристаллической структуры является ее координационное число (КЧ). Это число ближайших соседей центрального атома в структуре.

APF и CN наиболее распространенных кристаллических структур показаны ниже:

Кристаллическая структура	Фактор атомной упаковки	Координационный номер ( Геометрия )
Алмазный кубический	0.34	4 ( Тетраэдр )
Простой кубический	0.52 ^[10]	6 ( Октаэдр )
Объемноцентрированная кубическая (BCC)	0.68 ^[10]	8 ( Куб )
Гранецентрированный куб (ГЦК)	0.74 ^[10]	12 ( Кубооктаэдр )
Шестиугольная плотноупакованная (HCP)	0.74 ^[10]	12 ( Треугольный ортобикупол )

Эффективность упаковки FCC и HCP 74% — это максимально возможная плотность в элементарных ячейках, построенных из сфер только одного размера.

Межстраничные сайты [ править ]

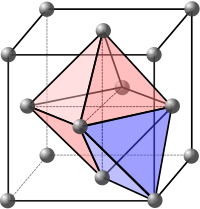
Межузельные узлы относятся к пустым пространствам между атомами в кристаллической решетке. Эти пространства могут заполняться противоположно заряженными ионами, образуя многоэлементные структуры. Они также могут быть заполнены атомами примесей или собственными междоузлиями с образованием межузельных дефектов .

Дефекты и примеси [ править ]

Реальные кристаллы имеют дефекты или нарушения в идеальном расположении, описанном выше, и именно эти дефекты критически определяют многие электрические и механические свойства реальных материалов.

Примеси [ править ]

Когда один атом заменяет один из основных атомных компонентов в кристаллической структуре, может последовать изменение электрических и тепловых свойств материала. ^[11] Примеси могут также проявляться в виде примесей электронного спина в некоторых материалах. Исследования магнитных примесей показывают, что на существенное изменение определенных свойств, таких как теплоемкость, могут влиять небольшие концентрации примеси, как, например, примеси в полупроводниковых ферромагнитных сплавах могут приводить к другим свойствам, как впервые было предсказано в конце 1960-х годов. ^[12]^[13]

Дислокации [ править ]

Дислокации в кристаллической решетке — это линейные дефекты, связанные с локальными полями напряжений. Дислокации допускают сдвиг при более низком напряжении, чем то, которое необходимо для идеальной кристаллической структуры. ^[14] Локальные поля напряжений приводят к взаимодействиям между дислокациями, которые затем приводят к деформационному упрочнению или холодной обработке .

Границы зерен [ править ]

Границы зерен — это границы раздела, где встречаются кристаллы разной ориентации. ^[4] Граница зерна представляет собой однофазную границу раздела, в которой кристаллы по обе стороны границы идентичны, за исключением ориентации. Иногда, хотя и редко, используется термин «граница кристаллита». Области границ зерен содержат те атомы, которые были смещены из своих исходных узлов решетки, дислокации и примеси, которые мигрировали к границе зерна с более низкой энергией.

Рассматривая границу зерна геометрически как границу раздела монокристалла, разрезанного на две части, одна из которых вращается, мы видим, что для определения границы зерна необходимо пять переменных. Первые два числа берутся из единичного вектора, определяющего ось вращения. Третья цифра обозначает угол поворота зерна. Последние два числа определяют плоскость границы зерна (или единичный вектор, перпендикулярный этой плоскости). ^[9]

Границы зерен нарушают движение дислокаций через материал, поэтому уменьшение размера кристаллитов является распространенным способом повышения прочности, как описано соотношением Холла-Петча . Поскольку границы зерен являются дефектами кристаллической структуры, они имеют тенденцию снижать электропроводность и теплопроводность материала. Высокая межфазная энергия и относительно слабая связь в большинстве границ зерен часто делают их предпочтительными местами для возникновения коррозии и выделения новых фаз из твердого тела. Они также важны для многих механизмов ползучести . ^[9]

Границы зерен обычно имеют ширину всего несколько нанометров. В обычных материалах кристаллиты достаточно велики, поэтому границы зерен составляют небольшую часть материала. Однако достижимы очень маленькие размеры зерен. В нанокристаллических твердых телах границы зерен составляют значительную объемную долю материала, что оказывает глубокое влияние на такие свойства, как диффузия и пластичность . В пределе мелких кристаллитов, когда объемная доля границ зерен приближается к 100%, материал перестает иметь кристаллический характер и, таким образом, становится аморфным твердым телом . ^[9]

Прогнозирование структуры [ править ]

Сложность прогнозирования стабильных кристаллических структур, основанная на знании только химического состава, долгое время была камнем преткновения на пути к полностью вычислительному проектированию материалов. Теперь, благодаря более мощным алгоритмам и высокопроизводительным вычислениям, структуры средней сложности можно прогнозировать с помощью таких подходов, как эволюционные алгоритмы , случайная выборка или метадинамика.

Кристаллические структуры простых ионных твердых веществ (например, NaCl или поваренной соли) уже давно рационализированы с точки зрения правил Полинга , впервые изложенных в 1929 году Лайнусом Полингом , которого многие с тех пор называют «отцом химической связи». ^[15] Полинг также рассмотрел природу межатомных сил в металлах и пришел к выводу, что около половины из пяти d-орбиталей в переходных металлах участвуют в связывании, а остальные несвязывающие d-орбитали отвечают за магнитные свойства. Таким образом, Полинг смог соотнести количество d-орбиталей в образовании связи с длиной связи, а также со многими физическими свойствами вещества. Впоследствии он ввел металлическую орбиталь, дополнительную орбиталь, необходимую для обеспечения неограниченного резонанса валентных связей между различными электронными структурами. ^[16]

В теории резонирующих валентных связей факторы, определяющие выбор одной из альтернативных кристаллических структур металла или интерметаллического соединения, вращаются вокруг энергии резонанса связей между межатомными положениями. Ясно, что некоторые виды резонанса будут вносить больший вклад (будут более механически стабильны, чем другие), и что, в частности, простое соотношение числа связей к числу положений будет исключительным. В результате принцип заключается в том, что особая стабильность связана с простейшими соотношениями или «числами связей»: 1 ⁄ 2 , 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 4 , 3 ⁄ 4 и т. д. Таким образом, выбор структуры и значения соотношения осей (определяющего относительные длины связей) являются результатом стремления атома использовать свою валентность при образовании устойчивых связей с простыми дробными числами связей. . ^[17]^[18]

Постулировав прямую корреляцию между концентрацией электронов и кристаллической структурой в бета-фазных сплавах, Хьюм-Розери проанализировал тенденции в температурах плавления, сжимаемости и длинах связей в зависимости от номера группы в периодической таблице, чтобы установить систему валентностей переходные элементы в металлическое состояние. Таким образом, эта обработка подчеркнула увеличение прочности связи в зависимости от номера группы. ^[19] Действие направленных сил было подчеркнуто в одной статье о связи между гибридами связей и металлическими структурами. Результирующая корреляция между электронной и кристаллической структурами суммируется одним параметром - весом d-электронов на гибридизованную металлическую орбиталь. «D-вес» рассчитывается как 0,5, 0,7 и 0,9 для структур ГЦК, ГПУ и ОЦК соответственно. Таким образом, связь между d-электронами и кристаллической структурой становится очевидной. ^[20]

При прогнозировании/моделировании кристаллической структуры обычно применяется периодичность, поскольку система считается неограниченной во всех направлениях. Начиная с триклинной структуры без каких-либо дополнительных свойств симметрии, можно заставить систему проявить некоторые дополнительные свойства симметрии, применив Второй закон Ньютона к частицам в элементарной ячейке и недавно разработанное динамическое уравнение для векторов периода системы. ^[21] (параметры решетки, включая углы), даже если система подвержена внешнему напряжению.

Полиморфизм [ править ]

Полиморфизм – это возникновение множественных кристаллических форм материала. Он содержится во многих кристаллических материалах, включая полимеры , минералы и металлы . Согласно правилам фазового равновесия Гиббса, эти уникальные кристаллические фазы зависят от интенсивных переменных, таких как давление и температура. Полиморфизм связан с аллотропией , которая относится к элементарным твердым веществам . Полная морфология материала описывается полиморфизмом и другими переменными, такими как габитус кристаллов , аморфная фракция или кристаллографические дефекты . Полиморфы обладают различной стабильностью и могут спонтанно и необратимо трансформироваться из метастабильной формы (или термодинамически нестабильной формы) в стабильную форму при определенной температуре. ^[22] Они также имеют разные температуры плавления , растворимость и картины дифракции рентгеновских лучей .

Хорошим примером этого является кварцевая форма диоксида кремния , или SiO ₂ . В подавляющем большинстве силикатов атом Si имеет тетраэдрическую координацию с помощью 4 атомов кислорода. Все кристаллические формы, кроме одной, включают тетраэдрические звенья {SiO ₄ }, связанные вместе общими вершинами в различном расположении. В разных минералах тетраэдры демонстрируют разную степень сетчатости и полимеризации. Например, они встречаются поодиночке, объединены в пары, в более крупные конечные кластеры, включая кольца, в цепочки, двойные цепочки, листы и трехмерные каркасы. В зависимости от структуры минералы подразделяются на группы. В каждой из 7 термодинамически стабильных кристаллических форм или полиморфов кристаллического кварца только 2 из 4 ребер тетраэдров {SiO ₄ } являются общими с другими, что дает чистую химическую формулу кремнезема: SiO ₂ .

Другим примером является элементарное олово (Sn), которое податливо при температуре окружающей среды, но становится хрупким при охлаждении. Такое изменение механических свойств связано с существованием двух его основных аллотропов , α- и β-олова. Два аллотропа , встречающиеся при нормальном давлении и температуре, α-олово и β-олово, более известны как серое олово и белое олово соответственно. Еще два аллотропа, γ и σ, существуют при температуре выше 161 ° C и давлении выше нескольких ГПа. ^[23] Белое олово является металлическим и представляет собой стабильную кристаллическую форму при комнатной температуре или выше. При температуре ниже 13,2 °C олово существует в серой форме, имеющей кубическую кристаллическую структуру алмаза, подобную алмазу , кремнию или германию . Серое олово вообще не имеет металлических свойств, представляет собой тускло-серый порошкообразный материал и имеет мало применений, за исключением нескольких специализированных полупроводниковых применений. ^[24] Хотя температура α-β-превращения олова номинально составляет 13,2 °C, примеси (например, Al, Zn и т. д.) понижают температуру перехода значительно ниже 0 °C, а при добавлении Sb или Bi превращение может вообще не произойти. ^[25]

Физические свойства [ править ]

Двадцать из 32 классов кристаллов являются пьезоэлектрическими , а кристаллы, принадлежащие к одному из этих классов (точечные группы), проявляют пьезоэлектричество . Все пьезоэлектрические классы лишены инверсионной симметрии . Любой материал приобретает диэлектрическую поляризацию при приложении электрического поля, но вещество, которое имеет такое естественное разделение зарядов даже в отсутствие поля, называется полярным материалом. Является ли материал полярным или нет, определяется исключительно его кристаллической структурой. Только 10 из 32 точечных групп являются полярными . Все полярные кристаллы пироэлектрики , поэтому 10 классов полярных кристаллов иногда называют пироэлектрическими классами.

Есть несколько кристаллических структур, в частности структура перовскита , которые демонстрируют сегнетоэлектрическое поведение. Это аналог ферромагнетизма , поскольку при отсутствии электрического поля при производстве сегнетоэлектрический кристалл не проявляет поляризации. При приложении электрического поля достаточной величины кристалл становится постоянно поляризованным. Эту поляризацию можно обратить вспять достаточно большим противозарядом, точно так же, как можно обратить вспять ферромагнетик. Однако, хотя их и называют сегнетоэлектриками, эффект обусловлен кристаллической структурой (а не наличием черного металла).

См. также [ править ]

Зона Бриллюэна – примитивная ячейка в обратной пространственной решетке кристалла.
Кристаллическая инженерия
Рост кристаллов - основной этап процесса кристаллизации.
Кристаллографическая база данных
Дробные координаты
Фазы Франка – Каспера
Обозначение Германа – Могена - обозначение для обозначения симметрии в точечных группах, плоских группах и пространственных группах.
Рост пьедестала с лазерным нагревом - метод выращивания кристаллов
Жидкий кристалл - состояние вещества, обладающее свойствами как обычных жидкостей, так и кристаллов.
Функция Паттерсона - функция, используемая для решения фазовой проблемы в рентгеновской кристаллографии.
Таблица Менделеева (кристаллическая структура) - (для элементов, которые являются твердыми при стандартной температуре и давлении) дает кристаллическую структуру наиболее термодинамически стабильной формы (форм) в этих условиях. Во всех остальных случаях приведенная структура относится к элементу при температуре его плавления.
Примитивная ячейка - повторяющаяся единица, образованная векторами, охватывающими точки решетки.
Затравочный кристалл – небольшой кусочек монокристалла, используемый для инициирования роста более крупного кристалла.
Ячейка Вигнера – Зейтца - примитивная ячейка кристаллической решетки с примененным разложением Вороного.

Ссылки [ править ]

^ Jump up to: ^а ^б ^с Хук, младший; Холл, HE (2010). Физика твердого тела . Манчестерская серия по физике (2-е изд.). Джон Уайли и сыновья. ISBN 9780471928041 .
^ Уэст, Энтони Р. (1999). Основная химия твердого тела (2-е изд.). Уайли. п. 1. ISBN 978-0-471-98756-7 .
^ Международные таблицы по кристаллографии (2006). Том А, Симметрия пространственной группы.
^ Jump up to: ^а ^б ^с Энциклопедия физики (2-е издание), Р.Г. Лернер , Г.Л. Тригг, издатели VHC, 1991, ISBN (издательская компания) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
^ «4. Прямые и обратные решетки» . CSIC Кафедра кристаллографии и структурной биологии . 6 апреля 2017 г. Проверено 18 мая 2017 г.
^ Эдингтон, JW (1975). Дифракция электронов в электронном микроскопе . дои : 10.1007/978-1-349-02595-4 . ISBN 978-0-333-18292-5 .
^ Эшкрофт, Н. ; Мермин, Д. (1976). «Глава 7». Физика твердого тела . Брукс/Коул (Thomson Learning, Inc.). ISBN 978-0030493461 .
^ Jump up to: ^а ^б Дональд Э. Сэндс (1994). «§4-2 Винтовые оси и §4-3 Плоскости скольжения» . Введение в кристаллографию (переиздание В. А. Бенджамина с исправлениями, изд. 1975 г.). Курьер-Дувр. стр. 70–71. ISBN 978-0486678399 .
^ Jump up to: ^а ^б ^с ^д Паркер, CB, изд. (1994). Энциклопедия физики МакГроу Хилла (2-е изд.). МакГроу-Хилл. ISBN 978-0070514003 .
^ Jump up to: ^а ^б ^с ^д Эллис, Артур Б.; и др. (1995). Преподавание общей химии: помощник по материаловедению (3-е изд.). Вашингтон, округ Колумбия: Американское химическое общество. ISBN 084122725X .
^ Каллай, Никола (2000). Межфазная динамика . ЦРК Пресс. ISBN 978-0824700065 .
^ Хоган, CM (1969). «Плотность состояний изоляционного ферромагнитного сплава». Физический обзор . 188 (2): 870–874. Бибкод : 1969PhRv..188..870H . дои : 10.1103/PhysRev.188.870 .
^ Чжан, XY; Зуль, Х (1985). «Удвоение периода спиновых волн и хаос при поперечной накачке». Физический обзор А. 32 (4): 2530–2533. Бибкод : 1985PhRvA..32.2530Z . дои : 10.1103/PhysRevA.32.2530 . ПМИД 9896377 .
^ Кортни, Томас (2000). Механическое поведение материалов . Лонг Гроув, Иллинойс: Waveland Press. п. 85. ИСБН 978-1-57766-425-3 .
^ Л. Полинг (1929). «Принципы, определяющие строение сложных ионных кристаллов». Дж. Ам. хим. Соц. 51 (4): 1010–1026. дои : 10.1021/ja01379a006 .
^ Полинг, Лайнус (1938). «Природа межатомных сил в металлах». Физический обзор . 54 (11): 899–904. Бибкод : 1938PhRv...54..899P . дои : 10.1103/PhysRev.54.899 .
^ Полинг, Лайнус (1947). «Атомные радиусы и межатомные расстояния в металлах». Журнал Американского химического общества . 69 (3): 542–553. дои : 10.1021/ja01195a024 .
^ Полинг, Л. (1949). «Теория резонирующей валентной связи металлов и интерметаллических соединений» . Труды Королевского общества А. 196 (1046): 343–362. Бибкод : 1949RSPSA.196..343P . дои : 10.1098/rspa.1949.0032 .
^ Хьюм-Ротери, В.; Ирвинг, HM; Уильямс, RJP (1951). «Валентности переходных элементов в металлическом состоянии». Труды Королевского общества А. 208 (1095): 431. Бибкод : 1951RSPSA.208..431H . дои : 10.1098/rspa.1951.0172 . S2CID 95981632 .
^ Альтманн, СЛ; Коулсон, Калифорния; Хьюм-Ротери, В. (1957). «О связи между гибридами связи и металлическими структурами». Труды Королевского общества А. 240 (1221): 145. Бибкод : 1957RSPSA.240..145А . дои : 10.1098/rspa.1957.0073 . S2CID 94113118 .
^ Лю, Банда (2015). «Динамические уравнения для векторов периода в периодической системе при постоянном внешнем напряжении». Может. Дж. Физ. 93 (9): 974–978. arXiv : cond-mat/0209372 . Бибкод : 2015CaJPh..93..974L . дои : 10.1139/cjp-2014-0518 . S2CID 54966950 .
^ Переход от анатаза к рутилу ART, в J. Mat. наук.
^ Молодец, А.М.; Набатов, С.С. (2000). «Термодинамические потенциалы, диаграмма состояния и фазовые переходы олова при ударном сжатии». Высокая температура . 38 (5): 715–721. дои : 10.1007/BF02755923 . S2CID 120417927 .
^ Холлеман, Арнольд Ф.; Виберг, Эгон; Виберг, Нильс (1985). «Жесть». Учебник неорганической химии (на немецком языке) (91–100 изд.). Вальтер де Грюйтер. стр. 793–800. ISBN 978-3-11-007511-3 .
^ Шварц, Мел (2002). «Олово и сплавы, свойства». Энциклопедия материалов, деталей и отделки (2-е изд.). ЦРК Пресс. ISBN 978-1-56676-661-6 .

Внешние ссылки [ править ]

СМИ, связанные с кристаллическими структурами, на Викискладе?

[Solid_State_Physics_2010-1] Jump up to: ^а ^б ^с Хук, младший; Холл, HE (2010). Физика твердого тела . Манчестерская серия по физике (2-е изд.). Джон Уайли и сыновья. ISBN 9780471928041 .

[2] Уэст, Энтони Р. (1999). Основная химия твердого тела (2-е изд.). Уайли. п. 1. ISBN 978-0-471-98756-7 .

[Space-group_symmetry-3] Международные таблицы по кристаллографии (2006). Том А, Симметрия пространственной группы.

[Physics_1991-4] Jump up to: ^а ^б ^с Энциклопедия физики (2-е издание), Р.Г. Лернер , Г.Л. Тригг, издатели VHC, 1991, ISBN (издательская компания) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3

[5] «4. Прямые и обратные решетки» . CSIC Кафедра кристаллографии и структурной биологии . 6 апреля 2017 г. Проверено 18 мая 2017 г.

[6] Эдингтон, JW (1975). Дифракция электронов в электронном микроскопе . дои : 10.1007/978-1-349-02595-4 . ISBN 978-0-333-18292-5 .

[7] Эшкрофт, Н. ; Мермин, Д. (1976). «Глава 7». Физика твердого тела . Брукс/Коул (Thomson Learning, Inc.). ISBN 978-0030493461 .

[Sands-8] Jump up to: ^а ^б Дональд Э. Сэндс (1994). «§4-2 Винтовые оси и §4-3 Плоскости скольжения» . Введение в кристаллографию (переиздание В. А. Бенджамина с исправлениями, изд. 1975 г.). Курьер-Дувр. стр. 70–71. ISBN 978-0486678399 .

[Physics_1994-9] Jump up to: ^а ^б ^с ^д Паркер, CB, изд. (1994). Энциклопедия физики МакГроу Хилла (2-е изд.). МакГроу-Хилл. ISBN 978-0070514003 .

[Ellis-10] Jump up to: ^а ^б ^с ^д Эллис, Артур Б.; и др. (1995). Преподавание общей химии: помощник по материаловедению (3-е изд.). Вашингтон, округ Колумбия: Американское химическое общество. ISBN 084122725X .

[11] Каллай, Никола (2000). Межфазная динамика . ЦРК Пресс. ISBN 978-0824700065 .

[12] Хоган, CM (1969). «Плотность состояний изоляционного ферромагнитного сплава». Физический обзор . 188 (2): 870–874. Бибкод : 1969PhRv..188..870H . дои : 10.1103/PhysRev.188.870 .

[13] Чжан, XY; Зуль, Х (1985). «Удвоение периода спиновых волн и хаос при поперечной накачке». Физический обзор А. 32 (4): 2530–2533. Бибкод : 1985PhRvA..32.2530Z . дои : 10.1103/PhysRevA.32.2530 . ПМИД 9896377 .

[14] Кортни, Томас (2000). Механическое поведение материалов . Лонг Гроув, Иллинойс: Waveland Press. п. 85. ИСБН 978-1-57766-425-3 .

[Paulingsrules-15] Л. Полинг (1929). «Принципы, определяющие строение сложных ионных кристаллов». Дж. Ам. хим. Соц. 51 (4): 1010–1026. дои : 10.1021/ja01379a006 .

[16] Полинг, Лайнус (1938). «Природа межатомных сил в металлах». Физический обзор . 54 (11): 899–904. Бибкод : 1938PhRv...54..899P . дои : 10.1103/PhysRev.54.899 .

[17] Полинг, Лайнус (1947). «Атомные радиусы и межатомные расстояния в металлах». Журнал Американского химического общества . 69 (3): 542–553. дои : 10.1021/ja01195a024 .

[18] Полинг, Л. (1949). «Теория резонирующей валентной связи металлов и интерметаллических соединений» . Труды Королевского общества А. 196 (1046): 343–362. Бибкод : 1949RSPSA.196..343P . дои : 10.1098/rspa.1949.0032 .

[19] Хьюм-Ротери, В.; Ирвинг, HM; Уильямс, RJP (1951). «Валентности переходных элементов в металлическом состоянии». Труды Королевского общества А. 208 (1095): 431. Бибкод : 1951RSPSA.208..431H . дои : 10.1098/rspa.1951.0172 . S2CID 95981632 .

[20] Альтманн, СЛ; Коулсон, Калифорния; Хьюм-Ротери, В. (1957). «О связи между гибридами связи и металлическими структурами». Труды Королевского общества А. 240 (1221): 145. Бибкод : 1957RSPSA.240..145А . дои : 10.1098/rspa.1957.0073 . S2CID 94113118 .

[21] Лю, Банда (2015). «Динамические уравнения для векторов периода в периодической системе при постоянном внешнем напряжении». Может. Дж. Физ. 93 (9): 974–978. arXiv : cond-mat/0209372 . Бибкод : 2015CaJPh..93..974L . дои : 10.1139/cjp-2014-0518 . S2CID 54966950 .

[22] Переход от анатаза к рутилу ART, в J. Mat. наук.

[23] Молодец, А.М.; Набатов, С.С. (2000). «Термодинамические потенциалы, диаграмма состояния и фазовые переходы олова при ударном сжатии». Высокая температура . 38 (5): 715–721. дои : 10.1007/BF02755923 . S2CID 120417927 .

[24] Холлеман, Арнольд Ф.; Виберг, Эгон; Виберг, Нильс (1985). «Жесть». Учебник неорганической химии (на немецком языке) (91–100 изд.). Вальтер де Грюйтер. стр. 793–800. ISBN 978-3-11-007511-3 .

[25] Шварц, Мел (2002). «Олово и сплавы, свойства». Энциклопедия материалов, деталей и отделки (2-е изд.). ЦРК Пресс. ISBN 978-1-56676-661-6 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

v т и Фундаментальные аспекты материаловедения
Materials science	Structure Properties Processing Performance
Classes of materials	Ceramics Glass Semiconductors Composites Metal Alloys Polymers
Analysis methods	Characterization analysis Phase diagram
Material characteristics	Crystal structure Electronic structure Microstructure

v т и Кристаллические системы
Bravais lattice Crystallographic point group
Seven 3D systems	triclinic (anorthic) monoclinic orthorhombic tetragonal trigonal & hexagonal cubic (isometric)
Four 2D systems	oblique rectangular square hexagonal